当前位置： 首页 > news >正文

强联通分量（重制版）

news 2025/8/12 15:20:26

qwq博主太忙了导致以前只发了一个低配版，现在我要重制了

本文将会详细讲到强联通分量（SCC）的基本概念、Tarjan算法、Kosaraju算法、缩点法、例题受欢迎的牛（虽然为USACO但没有farmer John）、还有网络协议（来自IOI1996），但我不会讲Gabow算法（三个算法掌握一个就可以了，这三算法效率上差不多，似乎Tarjan更受欢迎，Kosaraju也是一个很多人用的算法），那现在开始吧水完内容开始正题

（如果有任何不对的地方，请各位指出，博主会尽量修缮的）

基本概念

何为强联通分量

什么？你连图都不会！那就别来学了

强联通分量是个图论里面的内容，但他不是个算法，强联通分量是指在一个有向图内（注意！一定是有向图！无向图是没有强联通分量的，待会会解释）的子图，这个子图满足以下特点：

  1. 这个子图内任意两点可互相到达（所以无向图没有强联通分量，因为无向图本来就可以互相到达）
  2. 在这个有向图内，没有更大的满足条件一的另外一个子图包含这个子图
  3. 所以一个点只要他满足条件二，那么他自己就是一个强联通分量

强联通分量的一些性质

性质是个很重要的东西，能够让你灵活运用算法，接下来我将介绍一下几个比较重要的性质（博主认为，欢迎反驳和指正）

  1. 强联通分量内部必定存在环路
  2. 同一个图内的一个顶点只能属于一个强联通分量
  3. 如果一个强联通分量D1指向另一个强联通分量D2，那么D2回不到D1
  4. （这个性质会关系到后面缩点法的学习，听不懂没关系，记着到后面就懂了，但是十分重要）如果把强联通分量视为单一一个点，那么所有强联通分量构成的新图就是一个有向无环图（DAG）

如果你看懂了上面的内容，那么恭喜你，你已经对强联通分量有了基础的理解了（水分很高哈哈哈）

Tarjan算法

前言

没错，这就是举世闻名的Tarjan（音译Taijian）算法，他可以帮你解决如何求强联通分量（下面是水分，不想看的可以跳过），连漂亮国满天星上将*********用了都说好，更多内容，敬请观看“Tarjan算法传奇”

核心

Tarjan 算法的核心是为每个节点维护两个重要的值：

  1. dfn[u] (Discovery Time)：表示节点 u 在 DFS 遍历中被首次访问的时间戳。可以理解为节点的“序号”，它记录了节点被访问的先后顺序。

  2. low[u] (Lowest Link)：表示从节点 u 出发，在 DFS 树中能到达的最小的 dfn 值。这个值可能来自 u 的后代节点，通过一条回边（Back Edge）指向 DFS 树中更上层的节点。

当一个节点的 dfn 值等于 low 值时，就意味着以该节点为根的子树中的所有节点构成了一个强连通分量。

看不懂去看下面的通俗讲解版

步骤

作者太多事情（懒）了，所以我们直接上干货，废话不多说，上代码！！！！！！！！！！！！！

#include <bits/stdc++.h>//万能火车头const int MAXN = 10005; // 最大节点数，根据实际情况调整// 邻接表，存储图
std::vector<int> graph[MAXN];// Tarjan 算法所需变量
int dfn[MAXN];          // 节点 u 的 DFS 访问次序
int low[MAXN];          // 节点 u 能够回溯到的最小 dfn 值
bool inStack[MAXN];     // 标记节点是否在栈中
std::stack<int> s;      // 存储已访问但尚未确定 SCC 的节点
int timer;              // 计时器，用于记录 dfn
int scc_cnt;            // 强连通分量的数量// 存储找到的强连通分量
std::vector<std::vector<int>> sccs;// Tarjan 算法核心函数
void tarjan(int u) {// 1. 初始化当前节点 udfn[u] = low[u] = ++timer;s.push(u);inStack[u] = true;// 2. 遍历 u 的所有邻接点 vfor (int v : graph[u]) {// 如果 v 没有被访问过，继续 DFSif (dfn[v] == 0) {tarjan(v);// 回溯后，更新 low[u]。u 可以通过 v 到达 v 所能到达的最小 dfnlow[u] = std::min(low[u], low[v]);}// 如果 v 已经访问过，并且还在栈中，说明是回边else if (inStack[v]) {// 更新 low[u]。u 可以直接通过回边到达 v，所以 low[u] 可以是 dfn[v]low[u] = std::min(low[u], dfn[v]);}}// 3. 检查是否找到一个 SCC// 如果 dfn[u] == low[u]，说明 u 是一个 SCC 的根if (dfn[u] == low[u]) {scc_cnt++;std::vector<int> current_scc;int current_node;// 从栈中弹出所有属于该 SCC 的节点，直到 udo {current_node = s.top();s.pop();inStack[current_node] = false;current_scc.push_back(current_node);} while (current_node != u);sccs.push_back(current_scc);}
}// 主函数
int main() {int n, m; // n: 节点数, m: 边数std::cout << "请输入节点数 n 和边数 m: ";std::cin >> n >> m;std::cout << "请输入 m 条边 (u v):" << std::endl;for (int i = 0; i < m; ++i) {int u, v;std::cin >> u >> v;// 节点编号从 1 开始graph[u].push_back(v);}// 初始化所有变量std::fill(dfn, dfn + n + 1, 0);std::fill(inStack, inStack + n + 1, false);timer = 0;scc_cnt = 0;// 对每个未访问过的节点调用 tarjan 函数，防止图不连通（不过我倒还没见过不联通的图哟）for (int i = 1; i <= n; ++i) {if (dfn[i] == 0) {tarjan(i);}}// 输出结果std::cout << "\n找到的强连通分量总数: " << scc_cnt << std::endl;for (size_t i = 0; i < sccs.size(); ++i) {std::cout << "强连通分量 " << i + 1 << ": ";for (int node : sccs[i]) {std::cout << node << " ";}std::cout << std::endl;}return 0;//祖传火车尾巴
}
//抄代码的耗子尾汁

什么？DFS都不会？看看这个也是可以的（我什么时候也该出个重制版了qwq觉得看不懂去看人家的吧）

算法讲解通俗版

Tarjan 算法就像你去探索一个迷宫。

你有以下几个关键工具：

  1. 一个计时器：记录你进入每个房间的顺序。我们把这个顺序叫做 dfn。

  2. 一个定位器：这个定位器能告诉你，从当前房间出发，在不走出这个房间群的前提下，能回溯到最早进入的房间是哪一个。这个最早进入的房间的顺序号，我们称之为 low。

  3. 一个口袋：你走过的每个房间都会被放进这个口袋。（stank要生气了）

  4. 一个特殊标记：用来标记房间是否还在你的口袋里。

  5. DFS :用来帮助你走路

现在，我们开始逛迷宫：

  • 你进入一个新房间（节点 u）：

    • 你记录下进入这个房间的顺序（dfn[u]），比如第 5 个。

    • 你启动定位器，目前能回溯到的最早房间就是你自己，所以 low[u] 也设为 5。

    • 你把这个房间放进你的口袋里。

  • 你继续探索，从当前房间（u）走到下一个房间（v）：

    • 情况一：房间 v 是全新的（没被标记过）（DFS日常标记ing）。

      • 你进入 v 继续探索。

      • 等你在 v 里探索完，回到 u 的时候，你会更新你的定位器。你会问 v：“从你那里能回溯到的最早房间是哪个？”。然后你把答案和自己的 low 值进行比较，取其中更小的一个。这就像在如果我能通过你回到一个更早的房间，那我也能（废话ing）

    • 情况二：房间 v 已经探索过，并且还在你的口袋里（Tarjan日常更新ing）。

      • 这说明你遇到了一个环路！比如你从房间 A 走到 B，又从 B 走回了 A。

      • 你不用继续探索 v 了，但你要更新你的定位器。

      • 你直接把 v 的进入顺序（dfn[v]）和自己的 low 值进行比较，取更小的一个。既然我能直接走到你，那我就能回溯到你最早进入的那个房间，所以我的回溯能力至少和你一样强。（废话ing）

  • 你探索完了当前房间（u）的所有出口：

    • 这时，你检查自己的两个值：dfn[u]（进入顺序）和 low[u]（能回溯到的最早房间的顺序）。

    • 如果 dfn[u] 等于 low[u]，那么这就是一个强连通分量

    • 这时，你就找到了一个强连通分量。你需要把所有还在口袋里，并且比你晚进入的房间，连同你自己一起拿出来。它们就是一个完整的房间群。

结束我的演讲！

Kosaraju算法

不想讲了怎么办QWQ

那就不废话了（水不动了QWQ）

前言

Kosaraju 算法是另一种用于在有向图中寻找所有强连通分量（SCCs）的经典算法。它的核心思想是利用两次深度优先搜索（DFS）来完成任务。

与 Tarjan 算法只需要一次 DFS 不同，Kosaraju 算法的逻辑更加直观，但需要构建一个“反向图”。它的时间复杂度同样是 O(V+E)，其中 V 是顶点数，E 是边数。

Kosaraju 算法的核心思想

Kosaraju 算法的思路可以概括为以下三步：

  1. 第一次 DFS：对原图进行一次深度优先搜索，并在遍历过程中，按照节点完成遍历的顺序将所有节点压入一个栈中。这里的“完成遍历”指的是一个节点及其所有子节点都已经被访问完毕。

  2. 构建反向图：将原图中所有边的方向反转，得到一个反向图（或叫转置图）。

  3. 第二次 DFS：从栈顶开始，对反向图进行第二次深度优先搜索。每进行一次新的 DFS，就会找到一个强连通分量。

为什么这个方法有效？

这个算法之所以有效，基于一个重要的图论性质：

  • 如果一个图中的两个节点 u 和 v 属于同一个强连通分量，那么在反向图中，它们也属于同一个强连通分量。

第一次 DFS 的目的是为了找到一个合适的遍历顺序。这个顺序能保证在第二次 DFS 中，当你从栈顶的节点开始遍历时，你总会从一个强连通分量的“最高点”开始。

举个例子： 假设你有一个图，其中有一个强连通分量 C1 和一个强连通分量 C2，有一条边从 C1 指向 C2。

  • 在第一次 DFS 中，由于有这条边，C2 中的节点很可能会在 C1 中的节点之前完成遍历。因此，C1 中的节点会更早被压入栈，而 C2 中的节点会更晚被压入栈。

  • 栈顶的节点会是 C2 中的某个节点，因为它最后完成遍历。

  • 现在，我们对反向图进行第二次 DFS。由于边的方向反转了，C2 中没有边指向 C1。所以，当你从栈顶的节点（属于 C2）开始遍历时，你只能访问到 C2 中的所有节点，而无法进入 C1。这样，你就找到了一个完整的 SCC。

  • 当 C2 中的节点全部被访问后，我们从栈中弹出一个新的未访问节点，它必然属于 C1。此时，我们再次进行 DFS，这次就会找到 C1 这个 SCC。

Kosaraju 算法的优点和缺点

  • 优点：

    • 概念简单：它的逻辑比 Tarjan 算法更容易理解，步骤分明，便于初学者掌握。

    • 易于实现：因为它只涉及标准的 DFS，实现起来相对简单。

  • 缺点：

    • 需要两次 DFS：相比 Tarjan 算法的一次 DFS，它的效率稍低（虽然大O忽略常数（水））。

    • 需要额外存储空间：需要存储反向图，这会占用额外的内存空间。

在实际应用中，Tarjan 算法由于其仅需一次遍历的优势，通常被认为更高效。但 Kosaraju 算法因其清晰的逻辑，在教学和理解 SCC 概念时依然是一个非常重要的工具（水）

缩点法

还记得这个吗：（详见SCC性质4）

没错，这就是缩点法存在的原因

核心

我们把原图中的每一个强连通分量都看作一个全新的、单一的节点。

  • Why？

    • 在同一个强连通分量内部，所有节点都是可以互相到达的。这意味着，只要分量中的任何一个节点得到信息，这个分量内的所有节点都会得到信息。

    • 因此，从信息传递的角度来看，整个强连通分量可以被视为一个整体，一个“超级节点”（super Mario！）。

  • How？

    • 新图中的节点就是原图中的每一个强连通分量。

    • 如果原图中的一个节点 u 属于 SCC1，节点 v 属于 SCC2，并且存在一条从 u 到 v 的边，那么在新图中，就有一条从 SCC1 到 SCC2 的边。

    • 这个新图有一个非常重要的特性：它是一个有向无环图（DAG，Directed Acyclic Graph）。因为如果新图中存在环，那就意味着原图中对应的 SCC 们应该可以合并成一个更大的 SCC，这与我们已经找到“最大”的 SCC 相矛盾，所以证明了他是一个有向无环图（接着水）。

这就是缩点法。

上代码！

伪代码

就不给抄，你能咋滴？

// 新图的邻接表
vector<int> new_graph[MAX_SCC_COUNT];
set<pair<int, int>> edges; // 用于去重// 遍历原图中的每一条边 (u, v)
for (每个节点 u) {for (每个 u 的邻接点 v) {// 如果 u 和 v 属于不同的 SCCif (scc_id[u] != scc_id[v]) {// 添加新边 (scc_id[u], scc_id[v])if (edges.find({scc_id[u], scc_id[v]}) == edges.end()) {new_graph[scc_id[u]].push_back(scc_id[v]);edges.insert({scc_id[u], scc_id[v]});}}}
}

题目

受欢迎的FarmerJohn牛

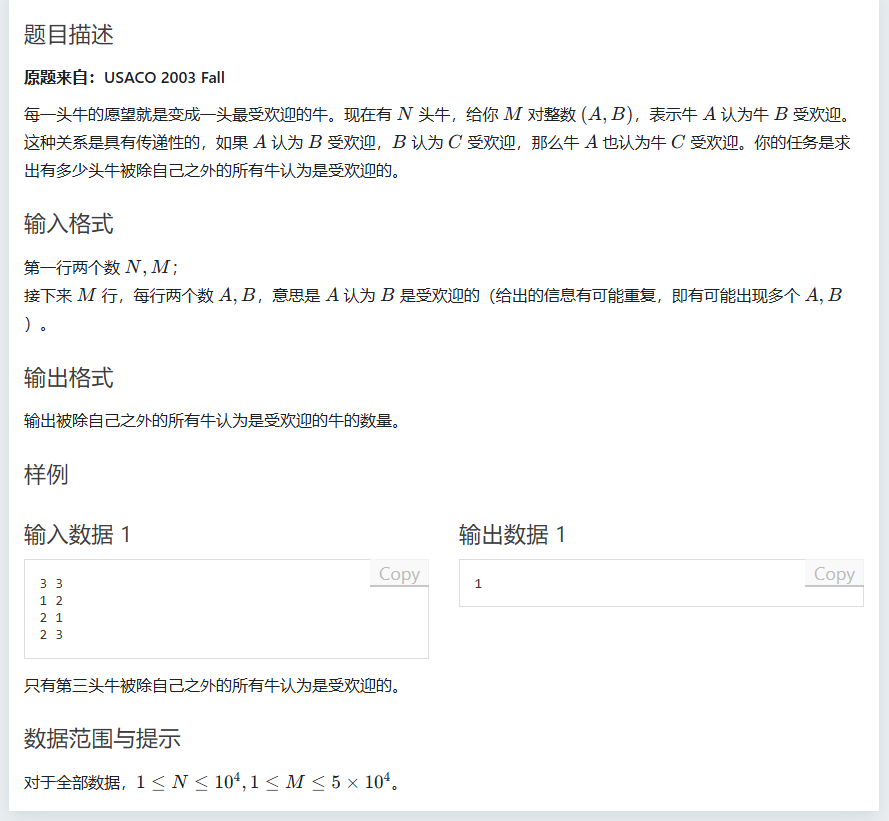题目

可以看到，这是十分适合强联通分量的，我们可以把它看成一个图，当A欢迎B那么A到B有一条有向边，第一个，强联通分量内所有的牛都是互相欢迎的，也就相当于一个强联通分量内的任意一头牛被该强联通分量内的其他牛欢迎，因此我们可以就此进行缩点，缩成一个有向无环图，我们又可以发现，根据性质3，这个新图中一个欢迎人家的“大牛”（缩点后的强联通分量）是不会被他欢迎的人欢迎的，所以，我们可以得出，答案是那些出度为0的“大牛”（骄傲的大牛是不会AKIOI的）所以，具体思路就出来了，先Tarjan加缩点法缩点，然后统计出度为0的大牛，然后统计这些大牛内的小牛个数，然后就可以AC勒！！！哈哈哈哈哈哈哈

代码来哩：

#include<stdio.h>
const int N=10010,M=50010;
struct node{int x,y,nxt;
}p[M];
int n,m,x,y,cs,ans,cnt,h[N],c[N],s[N],f[N],dep[M];
void in(int x,int y){p[++cnt].x=x,p[cnt].y=y;p[cnt].nxt=h[x],h[x]=cnt;
}
int find(int x){if(x==f[x]) return x;else return f[x]=find(f[x]);
}
void dfs(int x){for(int k=h[x];k;k=p[k].nxt){int y=p[k].y;if(!dep[y]){dep[y]=dep[x]+1;dfs(y);}int fx=find(x),fy=find(y);if(dep[fy]>0){if(dep[fy]<dep[fx]) f[fx]=fy;else f[fy]=fx;}}dep[x]=-1;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);in(x,y);}for(int i=1;i<=n;i++) f[i]=i;for(int i=1;i<=n;i++){if(!dep[i]){dep[i]=1;dfs(i);}}for(int i=1;i<=m;i++){int fx=find(p[i].x),fy=find(p[i].y);if(fx!=fy) c[fx]++;}for(int i=1;i<=n;i++) s[find(i)]++;for(int i=1;i<=n;i++){if(i==find(i)&&!c[i]){cs++;ans=s[i];}}if(cs==1) printf("%d\n",ans);else printf("0\n");return 0;
}

this is C,not C++,so there are not vector(水)

网络协议

IAKIOI!!!

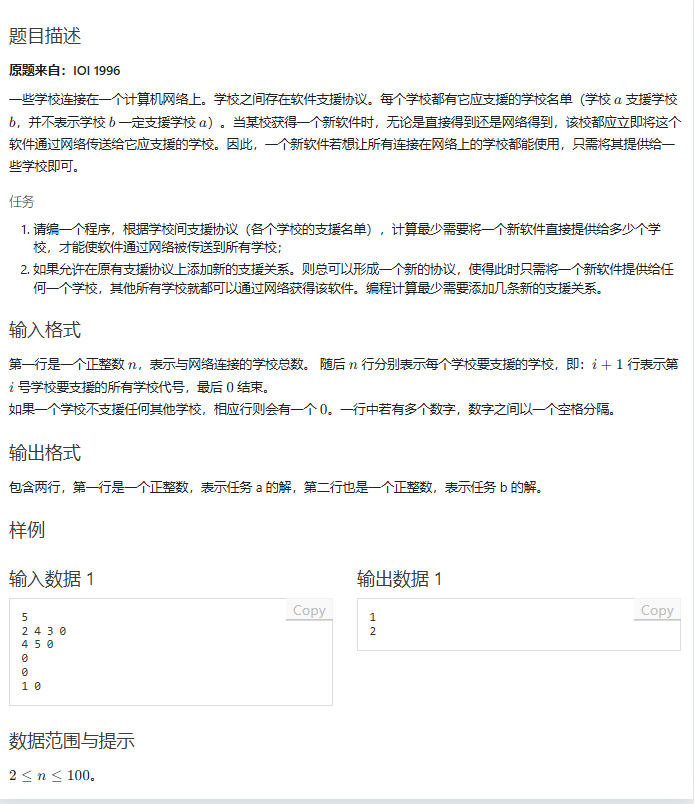
十分模版的题呀，可以发现，就是上面那题的“包装”，直接那上面那题的思路写就可以了

所以我为什么搬这道题呢，因为水

给你代码

就不给代码

总结

祝大家AC（稻花香里说RE，听取WA声一片）

再见！

http://www.dtcms.com/a/326786.html

相关文章：

  • 环境配置-拉取NVIDIA Docker镜像时出现401Unauthorized错误
  • 数据填报是什么？数据填报工具有哪些？
  • 黑马程序员mysql基础篇笔记
  • 自定义switch with icon
  • 使用Pytest进行接口自动化测试（三）
  • 深入了解torch框架
  • 数据类型 string
  • 算法题——IP地址分类与子网掩码
  • CobaltStrike安装和使用教程
  • Cobalt Strike的搭建和使用
  • JDK21虚拟线程和 Golang1.24协程的比较
  • STM32——system文件夹
  • Empire--安装、使用
  • 集团型企业如何统一管控子公司权限？
  • 奈飞工厂：算法优化实战​
  • 视频播放器哪个好用？视频播放器PotPlayer，KMP Player
  • 多轮会话记忆的核心挑战
  • 8.11下一代防火墙组网方案笔记
  • 使用MAS（Microsoft Activation Scripts）永久获得win10专业版和office全套
  • C++算法·前缀和
  • DCN之AP IGMP Snooping 原理与配置
  • P3917 异或序列 题解
  • Day01_QT编程20250811
  • while循环结合列表或字典
  • 二叉搜索树解析与实现
  • 快速设计简单嵌入式操作系统（3）：动手实操，基于STC8编写单任务执行程序，感悟MCU指令的执行过程
  • USB 标准请求
  • 机器学习——KMeans聚类实战案例解析
  • git配置proxy
  • Docker-09.Docker基础-Dockerfile语法