P3917 异或序列 题解

（本文中所有下标都是从1开始的，请注意辨别）

题面如下

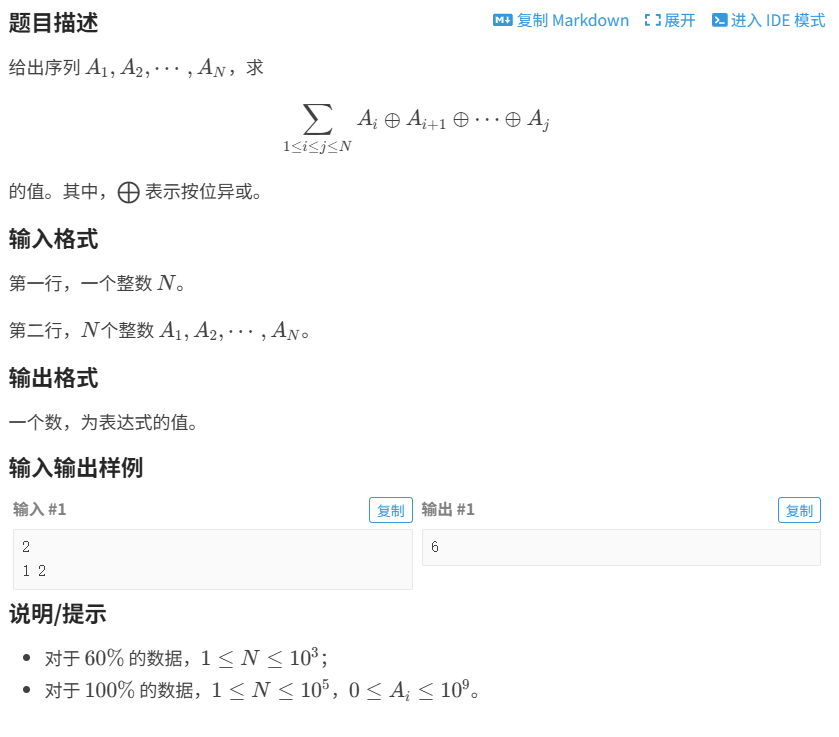
暴力模拟需要n^3，因为常数较小，TLE60pts

考虑优化

首先，异或是一种位运算，我们可以把每一个A表示为二进制，发现只要在不同二进制位分别计算就可以了

这使问题转化为了给定一个01串，求所有子串异或值之和（不考虑空串，下文同样）

其次，考虑枚举子串的方式，可以枚举每个子串的末位，使用一层循环

为什么枚举末位？因为这样可以保证之前的元素经过遍历，方便我们进行类似dp的操作

消耗一层循环，前面分解二进制位还提供了一个约30的大常数，我们没法再添加循环了

我们可以先观察一个01串，寻找其中的性质

0 1 0 0 1

尝试枚举末位，首先是0，显然子串只有一个，即0本身，对答案没有贡献，即不会改变答案

然后枚举到1，可以看到，子串有01，1两个，异或之后结果均为1，对答案贡献为2

接下来两个0，对答案的贡献也一样为2（有重复?）

再次枚举到1，发现有效的子串不能包含原来的1，所以贡献为3

此处就是这个算法的精髓，枚举到这个1之前，有效的子串包含且只包含第二位的那个1，所以子串的首位下标一定属于[1,2]，到这个1这里就恰恰相反，不能包含别的1，子串首位属于[3,5]

发现了吗，枚举到了1，那么可以选取的子串首位将成为原来的补集

可以设想，枚举到第三个1后，子串中可以包含另外两个1，也可以只有它自己一个1，所以区间[3,5]又被排除在外了

不难理解，一旦有一个新的1参与异或运算，必然改变运算中1的个数的奇偶性，所以取补集也是必然的

体现在代码上，我们不用弄清楚集合中包含哪些元素，只知道集合元素个数初始为0，每次遍历到1就对全集，即此处下标i取补集就可以了，设当前集合大小为sum，则有sum = i - sum

那么回归原题，我们为了处理每一位，得把sum开成数组，每次得出的结果还要乘以2^n再加到答案里，这是由二进制转回十进制

#include<bits/stdc++.h>
using namespace std;
int n;//数的个数
int a[114514];//每个数
int sum[50];//每一位当前的有效子串个数，即集合大小 
long long ans;//答案在这里 
int main(){memset(sum,0,sizeof(sum));//初始不存在有效的子串，均为0，此行可删除 cin>>n;for(int i = 1;i<=n;i++){//输入 cin>>a[i];}for(int i = 1;i<=n;i++){//枚举子串的末位 int k = 1;//当前二进制位 for(int j = 1;j<=30;j++){//枚举二进制位 if(a[i]&k){//当前位为1 sum[j] = i-sum[j]; }ans+=sum[j]*k;//对答案的贡献值*2^jk<<=1;//进位 }}cout<<ans;//输出 return 0;
}

时间复杂度O（n）(常数约为30)

后记

对于这种考位运算的题，可以多考虑二进制分解，然后按位解决

本文作者是蒟蒻，如有错误请各位神犇指点
森林古猿出品，必属精品，请认准CSDN森林古猿1！