当前位置：首页 > news >正文

机器学习——标准化、归一化

news 2025/8/11 11:49:11

‘标准化’、‘归一化’ 属于 ‘数据转换（Data Transformation）’

目标：把数据变成适合算法处理的形态。

标准化与归一化详解

1. 引言

在机器学习、数据分析和深度学习中，特征的取值范围往往差异巨大。直接使用原始数据可能导致某些特征在计算距离、梯度下降等过程中对结果产生不成比例的影响。

假设我们要用机器学习预测房价，数据集中有两个特征：
房屋面积（㎡）房龄（年）
120 8
80 15
200 3
面积的数值范围大约是 80 ~ 200
房龄的数值范围大约是 3 ~ 15
如果直接把这两个特征送进一些模型，如：
在 基于距离的算法（KNN、K-means）中，面积差 120㎡ vs 80㎡ 的差异（40）远比房龄差 8 年 vs 15 年 的差异（7）大得多，距离计算时几乎全被“面积”主导，房龄的影响被弱化。
在 梯度下降优化中，面积的梯度变化会很大，而房龄的梯度变化很小，导致模型在训练中更关注面积特征，忽略房龄特征。
直观理解
归一化：把所有特征的值压缩到固定范围（比如 0~1），比例关系保留，但绝对大小不重要。
标准化：让特征围绕 0 分布，并按标准差进行缩放，适合服从正态分布的特征。
比如
面积可能变成 0.2 ~ 0.9
房龄可能变成 0.1 ~ 0.8
这样，两个特征在模型计算中的“话语权”更均衡，模型能更全面地考虑不同特征的作用。

房屋面积（㎡）	房龄（年）
120	8
80	15
200	3

为了避免这种问题，我们需要对数据进行 特征缩放（Feature Scaling），其中最常见的两种方法就是标准化和归一化。

2. 标准化（Standardization）

2.1 定义

标准化是将数据的分布调整为均值为 0、标准差为 1的分布，使其符合标准正态分布 N(0,1)。

2.2 公式

对于特征 x：

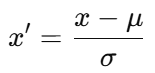
μ：特征的均值
σ：特征的标准差

2.3 特点

数据范围不固定（可能是 -3 到 3，也可能更大）。
适合假设数据服从正态分布的算法，例如线性回归、逻辑回归、SVM、KNN、PCA等。
对异常值较敏感，因为均值和标准差会被极端值拉动。

2.4 Python 示例

import numpy as np
from sklearn.preprocessing import StandardScaler# 模拟数据
X = np.array([[1, 200], [2, 300], [3, 400]])scaler = StandardScaler()
X_std = scaler.fit_transform(X)print("标准化后：\n", X_std)

3. 归一化（Normalization）

3.1 定义

归一化是将数据按比例压缩到固定范围（通常是 [0,1] 或 [-1,1]），保持特征之间的比例关系。

3.2 公式（Min-Max Normalization）

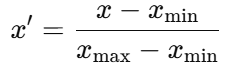
xmin：特征的最小值
xmax⁡：特征的最大值

3.3 特点

数据范围固定，通常在 [0,1]。
适合对距离敏感的算法（如 KNN、K-means、神经网络），因为它能防止大数值特征主导距离计算。
对异常值非常敏感，如果数据中有极端值，压缩后的大多数数据可能聚集在很小的区间。

3.4 Python 示例

import numpy as np
from sklearn.preprocessing import MinMaxScalerX = np.array([[1, 200], [2, 300], [3, 400]])scaler = MinMaxScaler(feature_range=(0, 1))
X_norm = scaler.fit_transform(X)print("归一化后：\n", X_norm)

4. 标准化 vs 归一化对比

对比维度	标准化（Standardization）	归一化（Normalization）
公式
范围	不固定	固定（[0,1]或[-1,1]）
对异常值敏感度	高	高
适用算法	假设数据正态分布的算法（线性回归、SVM、PCA等）	基于距离或梯度的算法（KNN、K-means、神经网络等）
结果分布	均值为0、标准差为1	保持比例但缩放到固定范围