算法训练营day44 动态规划⑪ 1143.最长公共子序列、1035.不相交的线、53. 最大子序和、392.判断子序列

        本篇是子序列篇章的续集，以继续巩固上一篇中的解题思想，以及开始编辑距离篇章的内容，简单说其实最主要的题目是本篇博客中的第一题

1143.最长公共子序列

        这题和最长重复子数组有一定的相似之处，区别在于本题为子序列（可以不连续），说在前面：这道题目在递推公式部分存在难点，可能不是很好想到这种方式，所以这个时候需要回到dp数组的概念和第五部分的模拟推导部分，如果实际推导过后，应该会多少好理解一些。其实大家如果做题连贯的话，可以很清楚的看到这道题和上篇博客最后一题在代码实现上的区别，就是在递推公式上多出来的两种情况，其实很像我们刚进入子序列篇章的第一和第二题

算法训练营day43 动态规划⑩ 300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组-CSDN博客

• 确定dp数组（dp table）以及下标的含义

        dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

• 确定递推公式

        主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

1. 如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
2. 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

        这个地方整体比较好理解，但是问题在于dp[i - 1][j]这类位置是否可以被计算出来，这个部分就要考虑dp数组的初始化 和 数组的遍历顺序了

• dp数组如何初始化

        text1[0, i-1]和空串的最长公共子序列自然是0，所以dp[i][0] = 0，同理dp[0][j]也是0。其他下标都是随着递推公式逐步覆盖，初始为多少都可以，那么就统一初始为0。

• 确定遍历顺序

        从递推公式，可以看出，有三个方向可以推出dp[i][j]，如图：

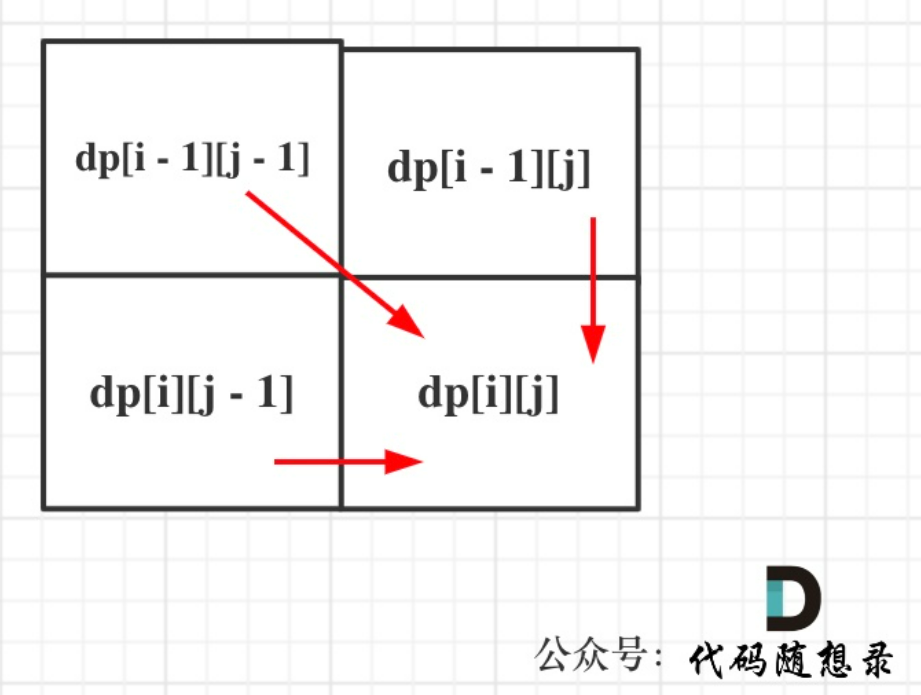
        那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

• 举例推导dp数组

以输入：text1 = "abcde", text2 = "ace" 为例，dp状态如图：

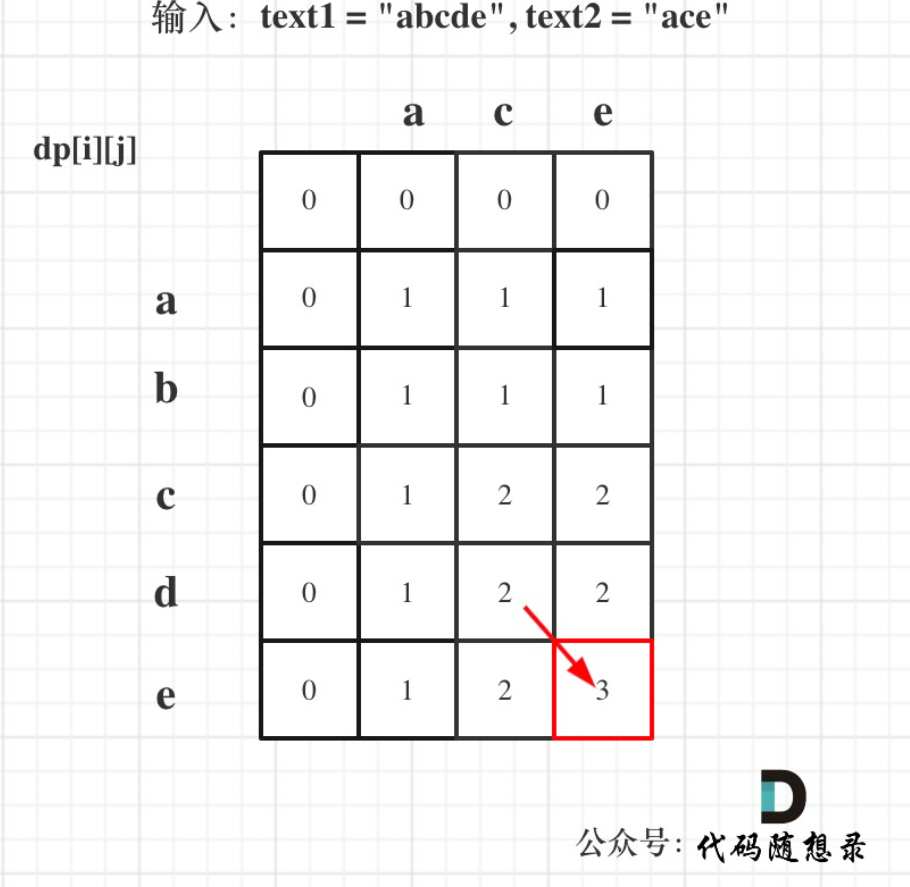
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:# 创建一个二维数组 dp，用于存储最长公共子序列的长度dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]# 遍历 text1 和 text2，填充 dp 数组for i in range(1, len(text1) + 1):for j in range(1, len(text2) + 1):if text1[i - 1] == text2[j - 1]:# 如果 text1[i-1] 和 text2[j-1] 相等，则当前位置的最长公共子序列长度为左上角位置的值加一dp[i][j] = dp[i - 1][j - 1] + 1else:# 如果 text1[i-1] 和 text2[j-1] 不相等，则当前位置的最长公共子序列长度为上方或左方的较大值dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])# 返回最长公共子序列的长度return dp[len(text1)][len(text2)]

1035.不相交的线

        和上道题完全一致！

class Solution:def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:dp = [[0] * (len(nums2)+1) for _ in range(len(nums1)+1)]for i in range(1, len(nums1)+1):for j in range(1, len(nums2)+1):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[-1][-1]

53. 最大子序和

        抛开动态规划，这道题是一道非常简单的题目可以使用贪心算法，但是有一个很核心的点需要注意，就是重新开始头部计算的时候，需要累加和为非正数的时候，不然会浪费掉一部分的正数值，这个部分想明白之后，就不会出问题了，相应的内容就是在结果输出的时候不要直接输出dp数组的最后一个值，动态规划如下：

• 确定dp数组（dp table）以及下标的含义

        dp[i]：包括下标i（以nums[i]为结尾）的最大连续子序列和为dp[i]。

• 确定递推公式

        dp[i]只有两个方向可以推出来：

1. dp[i - 1] + nums[i]，即：nums[i]加入当前连续子序列和
2. nums[i]，即：从头开始计算当前连续子序列和

        一定是取最大的，所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);

• dp数组如何初始化

        从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态，dp[0]就是递推公式的基础。根据dp[i]的定义，很明显dp[0]应为nums[0]即dp[0] = nums[0]。

• 确定遍历顺序

        递推公式中dp[i]依赖于dp[i - 1]的状态，需要从前向后遍历。

class Solution:def maxSubArray(self, nums: List[int]) -> int:dp = [0] * len(nums) # dp数组dp[0] = nums[0] # 初始化result = dp[0] # 记录结果for i in range(1, len(nums)):dp[i] = max(dp[i-1] + nums[i], nums[i]) #状态转移公式result = max(result, dp[i]) #result 保存dp[i]的最大值, 不要直接输出dp数组的最后一个值return result

392.判断子序列

        这道题本身的实现是简单的，是一个普通的双指针循环，下面的解法和最长公共子序列基本一致，这道题应该算是编辑距离的入门题目，因为从题意中我们也可以发现，只需要计算删除的情况，不用考虑增加和替换的情况。

        所以掌握本题的动态规划解法是对后面要讲解的编辑距离的题目打下基础。

• 确定dp数组（dp table）以及下标的含义

        dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。

• 确定递推公式

        在确定递推公式的时候，首先要考虑如下两种操作，整理如下：

        if (s[i - 1] == t[j - 1])  t中找到了一个字符在s中也出现了，那么dp[i][j] = dp[i - 1][j - 1] + 1;，因为找到了一个相同的字符，相同子序列长度自然要在dp[i-1][j-1]的基础上加1

        if (s[i - 1] != t[j - 1])  相当于t要删除元素，继续匹配，此时相当于t要删除元素，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了，即：dp[i][j] = dp[i][j - 1];

• dp数组如何初始化  

        这里大家已经可以发现，在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

        因为这样的定义在dp二维矩阵中可以留出初始化的区间，如图：

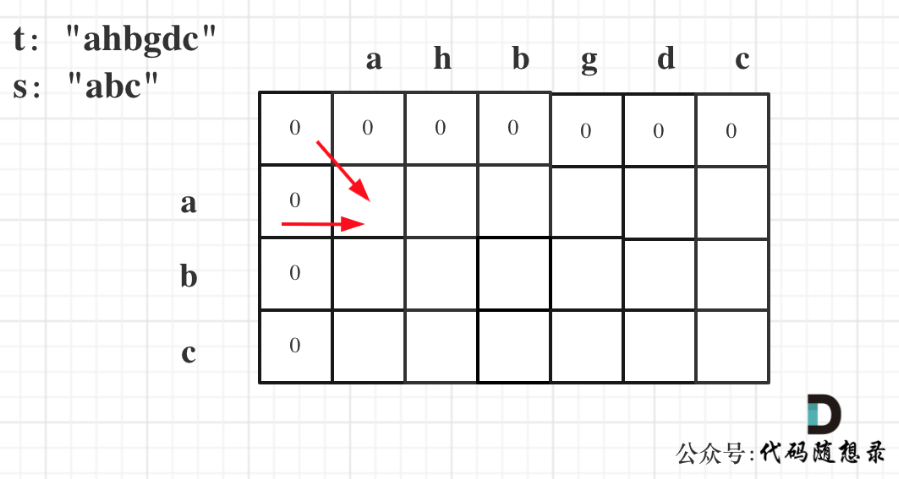
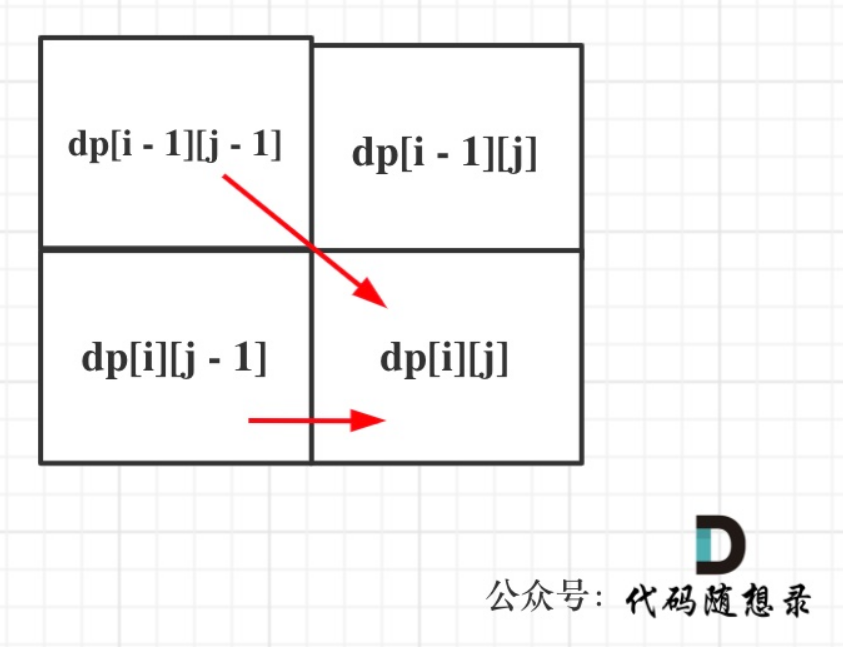
• 确定遍历顺序

        同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右

class Solution:def isSubsequence(self, s: str, t: str) -> bool:dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = dp[i][j-1]if dp[-1][-1] == len(s):return Truereturn False