人工智能系列（7）人工神经网络中的无监督学习

一. 无监督学习简介

神经网络的一个关键属性是能够从环境中学习，并在不断学习的过程中持续改善性能。在无监督学习（又称自组织学习，self-organized learning）中，网络无需外部教师提供目标输出，而是通过对输入数据进行模式识别，自动发现其中的结构与类别，从而实现自我组织与知识获取。这种方式在一定程度上模拟了人脑神经系统的工作机制，能够适应环境变化，并可应用于聚类、特征提取、数据可视化等任务，尤其适合对数据流进行实时处理与自适应更新的场景。

二. Hebbian 学习

a. Hebb定律基础：

Hebbian 学习源于 1949 年 Donald Hebb 提出的生物学习假说，其核心理念是：如果两个神经元在同一时间被激活，它们之间的连接会被加强；反之，若激活不同步，则连接权重会减弱。这一机制被概括为“fire together, wire together”，反映了生物神经系统中基于活动相关性的可塑性原理，也为人工神经网络中局部权重更新规则提供了理论基础，使网络能够在没有外部监督信号的情况下，通过统计相关性逐渐捕捉输入数据中的潜在模式与关联结构。

我们便基于此逻辑来实现无监督学习（即找到两个关联的神经元）：如果两个神经元同时激活 → 增强它们之间的连接；不同步 → 减弱连接。

b. Hebbian学习数学公式：

基本权重更新公式：

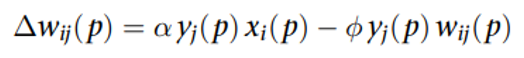
α 为学习率；存在的问题：权重会无限增长，解决方案：引入非线性遗忘因子∅。

c. Hebbian学习算法步骤：

i.初始化权重；

将初始突触权重设置为较小的随机值（即区间 [0, 1]）。将 α 和 ∅ 赋值为较小的正值。

ii.应用输入模式；

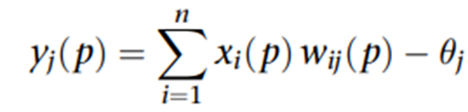
iii.更新权重；

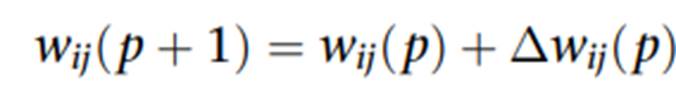
其中

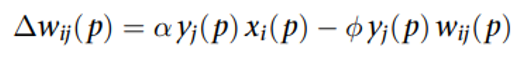
iv.迭代（i）（ii）直到权重值稳定。

三. 竞争学习

i. 概念

竞争学习是一种神经元相互竞争的学习机制，其中只有“赢家”神经元被激活（winner-takes-all），与 Hebbian 学习不同的是，输出层在一次响应中仅允许一个神经元处于激活状态。

ii. 自组织特征图

自组织特征图（SOM, Self-Organising Feature Map）的设计灵感源自人脑的大脑皮层结构。大脑皮层由数十亿个神经元和数千亿个突触构成，不同区域负责不同类型的感官与运动功能（如视觉、听觉、触觉、运动控制等），每种感官输入都会映射到皮层的特定区域，并且这种映射关系是通过神经元的自组织活动形成的，而非外部“教师”监督。这一原理被 Teuvo Kohonen 在 1980 年代引入人工神经网络领域，形成了 SOM 模型。SOM 通过无监督的竞争学习机制，将高维输入数据映射到低维（通常为二维）Kohonen 层，同时保持数据的拓扑结构：相似输入在映射平面上彼此靠近，不相似的则分开。

iii. Kohonen 网络结构与特性：

1. 网络初期邻域范围较大，随着训练逐步减小

在 SOM 训练初期，邻域范围设得较大，以便在网络中进行全局调整，使得映射拓扑能够快速成形。随着训练的进行，邻域半径会逐渐缩小，最终只影响最佳匹配单元（BMU）及其非常接近的邻居，从而实现局部精细化调整。即刚开始要做全局调整，让整体拓扑关系快速成形；后期逐步缩小邻域，进行局部微调，让映射更加精细。

2. 侧向连接进行竞争

Kohonen 网络的输出层神经元之间存在侧向连接（lateral connections），这种结构支持神经元之间相互激励与抑制，从而实现winner-takes-all（赢家通吃）机制。具体来说，当某个神经元成为 BMU（最佳匹配单元）时，会抑制其他神经元的响应，确保同一输入模式只激活一个核心神经元。这种竞争过程能有效避免多个神经元同时对相同模式敏感，保持映射结果的唯一性和稳定性。

3. 墨西哥帽函数调节邻居的激励与抑制

在更新权重时，SOM 通常采用墨西哥帽函数来调节邻域神经元的激励与抑制。该函数的形状类似中间高、周围低、再外围略高的曲线，使得 BMU 权重更新幅度最大，近邻神经元得到较小的正向更新，而远一些的神经元可能会被抑制。这种激励–抑制平衡有助于保持拓扑连续性，同时增强不同类别之间的分隔效果。

iv. 竞争学习更新规则：

1. 仅胜者神经元及其邻域更新权重；
2. 使用欧几里得距离作为匹配准则：

​

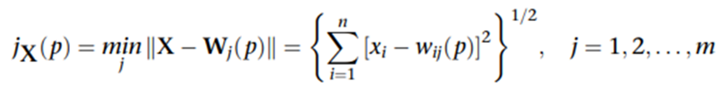
3.最小距离神经元为胜者，其权重向输入向量方向移动。

四. Kohonen 网络的学习算法步骤：

1. 初始化：小随机值初始化权重，设定学习率；
2. 激活与匹配：找出最接近输入向量的神经元；
3. 权重更新：

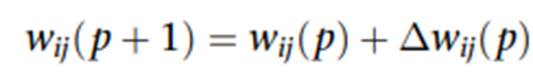
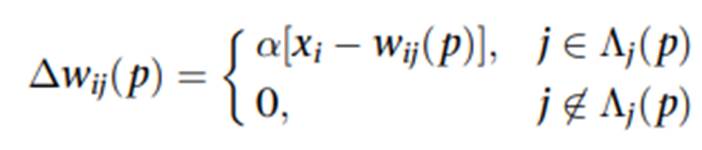
α是学习率，控制更新幅度;Λj(p)是邻域函数；

4.迭代：更新迭代次数并返回步骤2，直到权重收敛或无显著变化。