力扣经典算法篇-47-Pow(x, n)(快速幂思路）

1、题干

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：
输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：
输入：x = 2.10000, n = 3
输出：9.26100

示例 3：
输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：
-100.0 < x < 100.0
-231 <= n <= 231-1
n 是一个整数
要么 x 不为零，要么 n > 0 。
-104 <= xn <= 104

2、解题

本题求解x的n次幂，简单来说就是n个x相乘，但作为算法考察的目题目，肯定不会那么简答，下面通过快速幂的方法优化一下。

快速幂思路：
对于起始入参x，将前一次的计算的结果作为下一步的计算入参。这样可以在O（logn）的时间复杂度上得到优化。但是要注意n是奇偶数的情况。

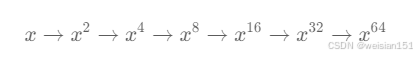
如：2的64次方求解。
传统做法：22222222=256。需要计算7次乘法操作。
快速幂做法：先22=4，在44=16，在1616=256。只需要计算3次乘法即可。

方法一：（快速幂 + 递归）

快速幂的求法，实际也是分治的思路。
注意：
求解快速幂，如果n%20，直接拿二分的结果相乘即可。如果n%21，二分的结果相乘后还要在乘以一次x。
如：4/2=2; 是2的4次幂可以直接使用2的2次幂结果相乘；但5/2=2; 这种情况就需要再乘以一次x才能得到正确结果。

代码示例：

public class Test54 {public static double myPow(double x, int n) {if (n == 0 || x == 1) {   // x为1或n==0可以快速返回1return 1;}double result = quickMul(x, n);   // 对求解return n > 0 ? result : 1 / result;     // 注意指数为负数要返回倒数}private static double quickMul(double x, int n) {if (n == 0) {     // 递归终止条件，n==0不可再分，因为相乘需要返回1，如果是相加一般返回0return 1;}double halfTemp = quickMul(x, n / 2);      // 求取一半指数时的答案，思路类似二分法return n % 2 == 0 ? halfTemp * halfTemp : halfTemp * halfTemp * x;    // 注意偶数直接相乘即可，基数还需要乘以x一次。}public static void main(String[] args) {double x = 2.00000;int n = 10;System.out.println(myPow(x, n));}
}

向阳前行，Dare To Be！！！