leetcode经典题目——单调栈
单调栈
739. 每日温度
739. 每日温度 - 力扣(LeetCode)
class Solution {public int[] dailyTemperatures(int[] temperatures) {Deque<Integer> stack = new ArrayDeque<>(); // 存下标int length = temperatures.length;int[] res = new int[length];for (int i = 0; i < length; i++) {int tmp = temperatures[i];while (!stack.isEmpty() && tmp > temperatures[stack.peek()]) {// 弹出栈顶元素,并计算距离Integer j = stack.pop();res[j] = i - j;}// 将当前遍历到的元素入栈stack.push(i);}return res;}
}在解决「每日温度」这类“寻找下一个更大元素”的问题时,单调栈是一种非常高效的解决方案。其核心在于维护一个单调递减的栈,栈中存储的是数组元素的下标。
具体流程如下:
- 遍历每个温度,对于当前元素,如果栈不为空且当前温度大于栈顶下标对应的温度,则说明找到了栈顶元素的下一个更高温度。
- 弹出栈顶元素,计算两者下标差,即为等待天数,并记录到结果中。
- 由于栈中元素按温度递减排列(单调性),每次只需比较当前元素与栈顶,无需再与之前元素比较。
- 栈中存储的是元素的下标而非值,这样可以方便地访问原数组数据并计算结果。
通过维护栈的单调性,该方法确保了每个元素最多只会入栈和出栈一次,时间复杂度为 O(n),空间复杂度为 O(n),是一种非常优雅且高效的解法。
496.下一个更大元素 I
496. 下一个更大元素 I - 力扣(LeetCode)
class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {int m = nums1.length;Stack<Integer> stack = new Stack<>();HashMap<Integer, Integer> hashMap = new HashMap<>();// 构建哈希表for (int num : nums2) {while (!stack.isEmpty() && stack.peek() < num) {hashMap.put(stack.pop(), num);}stack.push(num);}int[] res = new int[m];for (int i = 0; i < m; i++) {res[i] = hashMap.getOrDefault(nums1[i], -1);}return res;}
}解题思路:
虽然题目说到了nums1和nums2,但是其实我们可以发现,无非就是找到nums[i] 在 nums2中的位置j,然后在j开始遍历找到下一个比它大的数,那我还不如直接就遍历一遍nums2,找到每一个数的下一个比它大的数,并且用一个哈希表来记录每一个数下一个比它大的数,因为题目也说了nums1是nums2的子集,所以nums1中的元素肯定都是num2中的
那这样子就将题目拆解成遍历一遍nums2,找到每一个比它小的数
那是不是就可以使用单调栈来实现,每次遍历到一个元素就不断的和栈顶元素进行比较,因为这个元素如果大于栈顶的话是不是就说明它是栈顶元素的下一个元素
503.下一个更大元素II
503. 下一个更大元素 II - 力扣(LeetCode)
class Solution {public int[] nextGreaterElements(int[] nums) {Deque<Integer> stack = new ArrayDeque<>(); // 存储下标int length = nums.length;int[] res = new int[length];// 初始化resArrays.fill(res, -1);// 进行两次遍历for (int i = 0; i < length * 2; i++) {int num = nums[i % length]; // 当前遍历到的元素int idx = i % length; // 当前遍历到的下标// 当栈顶元素小于当前遍历到的元素的时候就说明找到了while (!stack.isEmpty() && nums[stack.peek()] < num) {int top = stack.pop();res[top] = num;}// 只有第一次遍历的时候才将当前元素入栈if (i < length) {stack.push(i);}}return res;}
}这道题的解题思路就是使用单调栈,每次将当前元素和栈顶元素进行比较,只要是大于栈顶元素就把栈顶元素弹出来,并记录下这个元素的下一个最大的元素,不过因为是循环数组,所以我们可以采用遍历两次的方式。
然后其实我们自己模拟一遍就会发现,经过第一次遍历之后,栈中只会保留第一遍遍历的时候找不到下一个比它大的元素的那些元素,所以我们可以直接在一个while循环中来实现,因为压根不会影响到第一次遍历已经找到的那些元素,不过第一遍遍历的时候需要将遍历到的元素入栈
42. 接雨水
42. 接雨水 - 力扣(LeetCode)
class Solution {public int trap(int[] height) {int len = height.length;int[] stack = new int[len]; //栈int top = -1; // 栈顶指针int res = 0;for (int i = 0; i < height.length; i++) {while (top != -1 && height[stack[top]] <= height[i]) {Integer midButton = height[stack[top]];top--;// 如果这两条柱是挨在一起的,也是没有雨水的if (top == -1) {break;}// 计算出高度Integer j = stack[top];int h = Math.min(height[j], height[i]) - midButton;// 计算体积res += h * (i - j - 1);}// 将当前元素进栈stack[++top] = i;}return res;}
}解题思路:使用单调栈,直接遍历一遍,只要遇到当前元素大于或是等于栈顶元素,就将栈顶元素出栈,并且判断栈是否是空,空的话说明是两条柱是挨在一起的,也是没有雨水的。
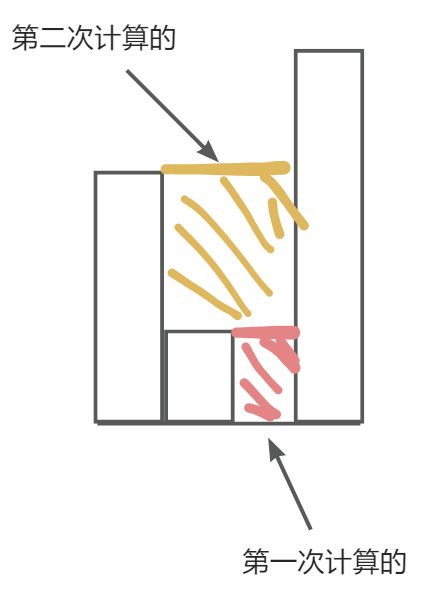
否则就是再将栈顶的元素作为左边柱子,当前元素为右边柱子,取短的那个,然后进行计算。(这里不用担心中间有多个雨水的情况,因为我们只计算到低的那个高度,其他的会留到下一次循环进行计算,这里可以自己画图理解一下)
84.柱状图中最大的矩形
84. 柱状图中最大的矩形 - 力扣(LeetCode)
class Solution {public int largestRectangleArea(int[] heights) {ArrayDeque<Integer> stack = new ArrayDeque<>();int maxArea = 0;int n = heights.length;for (int i = 0; i <= n; i++) {int h = (i == n) ? 0 : heights[i]; // 只是用来标记是否是最后一个元素// 当前遍历到的元素的面积已经确定while (!stack.isEmpty() && heights[stack.peek()] > h) {int height = heights[stack.pop()]; // 考虑递减情况int w = stack.isEmpty() ? i : (i - stack.peek() - 1);maxArea = Math.max(maxArea, height * w);}stack.push(i);}return maxArea;}
}解题思路:计算每一个高度的最大面积
使用一个栈,进行遍历,每次只要遍历到比栈顶元素小的元素,说明栈顶元素这个高度的面积已经确定了,所以就可以进行计算,高度确定,宽度就要看栈是否为空,因为如果原本给的数组就是递减的话,栈就是空的,宽度就是i,否则就是 (i - stack.peek() - 1)
