4深度学习Pytorch-神经网络--损失函数(sigmoid、Tanh、ReLU、LReLu、softmax)
目录
激活函数
1. Sigmoid
2. Tanh 函数(双曲正切)
3. ReLU 函数
4. Leaky ReLU (LReLU)
5. Softmax
总结对比表
损失函数选择
激活函数
激活函数是神经网络中每个神经元(节点)的核心组成部分。它接收上一层所有输入的加权和(加上偏置项),并产生该神经元的输出。其主要作用是引入非线性,使得神经网络能够学习和逼近任意复杂的函数关系。如果没有非线性激活函数,无论网络有多少层,最终都等价于一个线性变换(单层感知机),能力极其有限。
1. Sigmoid
-
公式:
-
原理: 将输入压缩到
(0, 1)区间。输出值可以被解释为概率(尤其是在二分类问题的输出层)。它平滑、易于求导。 -
特征:
-
输出范围: (0, 1)
-
单调递增: 函数值随输入增大而增大。
-
S型曲线: 中间近似线性,两端饱和(变化缓慢)。
-
导数:
最大值为0.25(当x=0时)。
-
-
缺点:
-
梯度消失: 当输入
x的绝对值很大时(处于饱和区),导数σ'(x)趋近于0。在反向传播过程中,梯度会逐层连乘这些接近0的小数,导致深层网络的梯度变得非常小甚至消失,使得网络难以训练(权重更新缓慢或停滞)。 -
信息丢失:输入100和输入10000经过sigmoid的激活值几乎都是等于 1 的,但是输入的数据却相差 100 倍。
-
输出非零中心化: 输出值始终大于0。这可能导致后续层的输入全为正(或全为负),使得权重更新时梯度全部朝同一方向(正或负)移动,降低收敛效率(呈“之”字形下降路径)。
-
计算相对较慢: 涉及指数运算。
-
-
函数绘制:
-
当
x -> -∞时,σ(x) -> 0(左水平渐近线 y=0)。 -
当
x = 0时,σ(0) = 0.5。 -
当
x -> +∞时,σ(x) -> 1(右水平渐近线 y=1)。 -
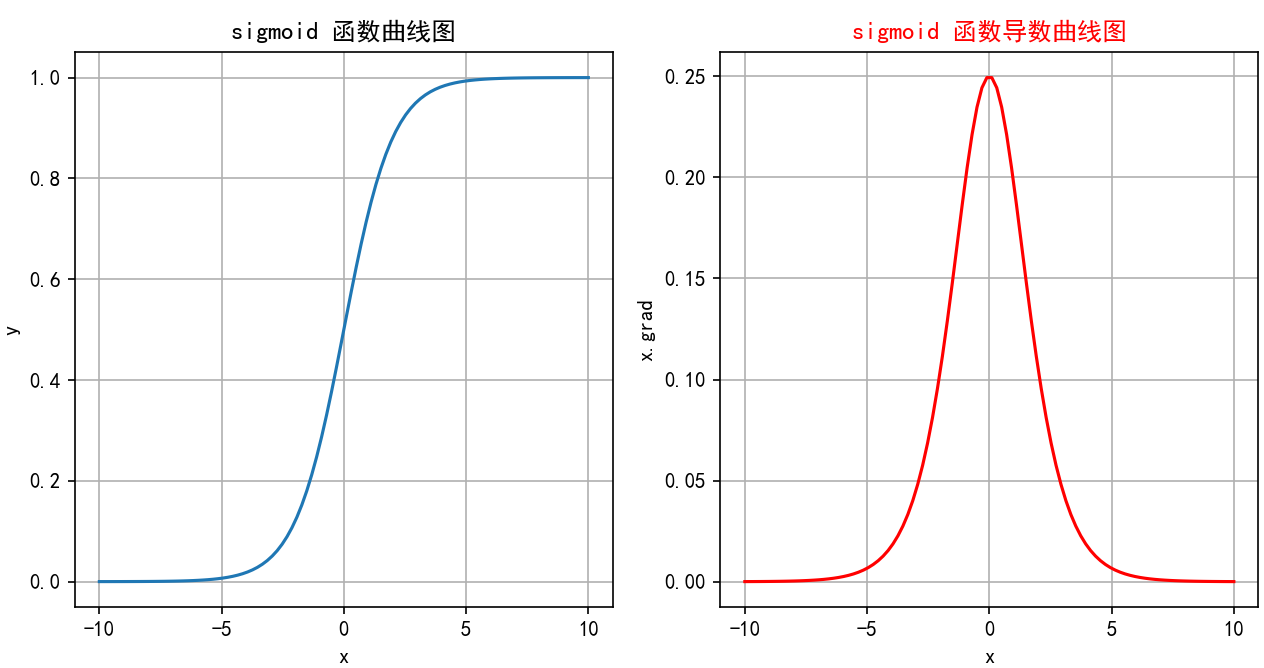
图像是一条平滑的、从接近0上升到接近1的S形曲线,关于点(0, 0.5)中心对称。导数曲线是一个钟形曲线,在x=0处达到峰值0.25,向两边迅速衰减到0。
-
2. Tanh 函数(双曲正切)
-
公式:
-
原理: 将输入压缩到
(-1, 1)区间。是Sigmoid函数的缩放和平移版本。解决了 Sigmoid 输出均值非零的问题,更适合作为隐藏层激活函数。 -
特征:
-
输出范围: (-1, 1)
-
单调递增: 函数值随输入增大而增大。
-
S型曲线: 中间近似线性,两端饱和。
-
零中心化: 输出关于原点对称(
tanh(-x) = -tanh(x))。这是相比于Sigmoid的主要优势,通常能使后续层的输入具有更理想的均值,有助于加速收敛。 -
导数:
tanh'(x) = 1 - tanh²(x),最大值为1(当x=0时)。
-
-
缺点:
-
梯度消失: 和Sigmoid类似,当
|x|很大时,导数趋近于0,仍然存在梯度消失问题(虽然比Sigmoid稍好,因为其导数值更大)。 -
计算相对较慢: 同样涉及指数运算。
-
-
函数绘制:
-
当
x -> -∞时,tanh(x) -> -1(左水平渐近线 y=-1)。 -
当
x = 0时,tanh(0) = 0。 -
当
x -> +∞时,tanh(x) -> 1(右水平渐近线 y=1)。 -
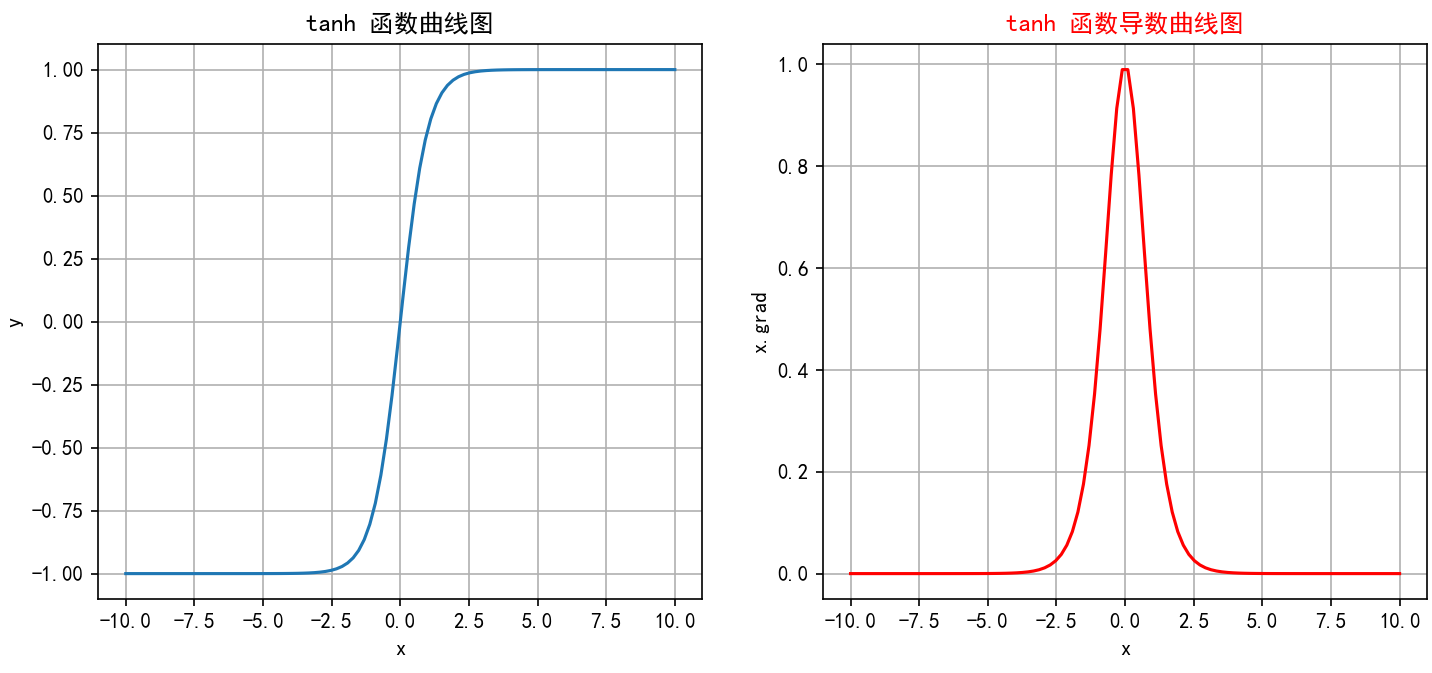
图像是一条平滑的、从接近-1上升到接近1的S形曲线,关于原点(0,0)中心对称。导数曲线是一个钟形曲线,在x=0处达到峰值1,向两边衰减到0。整体形状比Sigmoid更陡峭,饱和区变化更快。
-
3. ReLU 函数
-
公式:
-
原理: ReLU 是目前最常用的隐藏层激活函数之一,通过简单的线性分段
-
特征:
-
输出范围: [0, +∞)
-
计算极其高效: 只需比较和取最大值操作,没有指数等复杂运算。
-
缓解梯度消失: 在正区间 (
x > 0),导数为1,梯度可以无损地反向传播,有效缓解了梯度消失问题,使得深层网络训练成为可能。这是其成功的关键。 -
ReLU 函数的导数是分段函数:
-
生物学合理性: 更接近生物神经元的稀疏激活特性(只有一部分神经元被激活)。
-
稀疏激活:
时输出为 0,使网络具有 “稀疏性”(仅部分神经元激活),模拟生物神经元的工作模式。
-
-
缺点:
-
死亡ReLU (Dying ReLU): 在负区间 (
x < 0),导数为0。如果一个神经元的加权和输入在训练过程中大部分时间都小于0(例如,学习率过高或负的偏置过大),那么它的梯度在反向传播时始终为0,导致该神经元的权重无法再更新,永远“死亡”(输出恒为0,不再参与训练)。 -
输出非零中心化: 输出始终 >= 0。
-
在
x=0处不可导: 实践中通常将x=0处的导数设为0或1(通常设为0)。
-
-
函数绘制:
-
当
x < 0时,ReLU(x) = 0(沿x轴负半轴)。 -
当
x >= 0时,ReLU(x) = x(沿y=x直线在第一象限)。 -
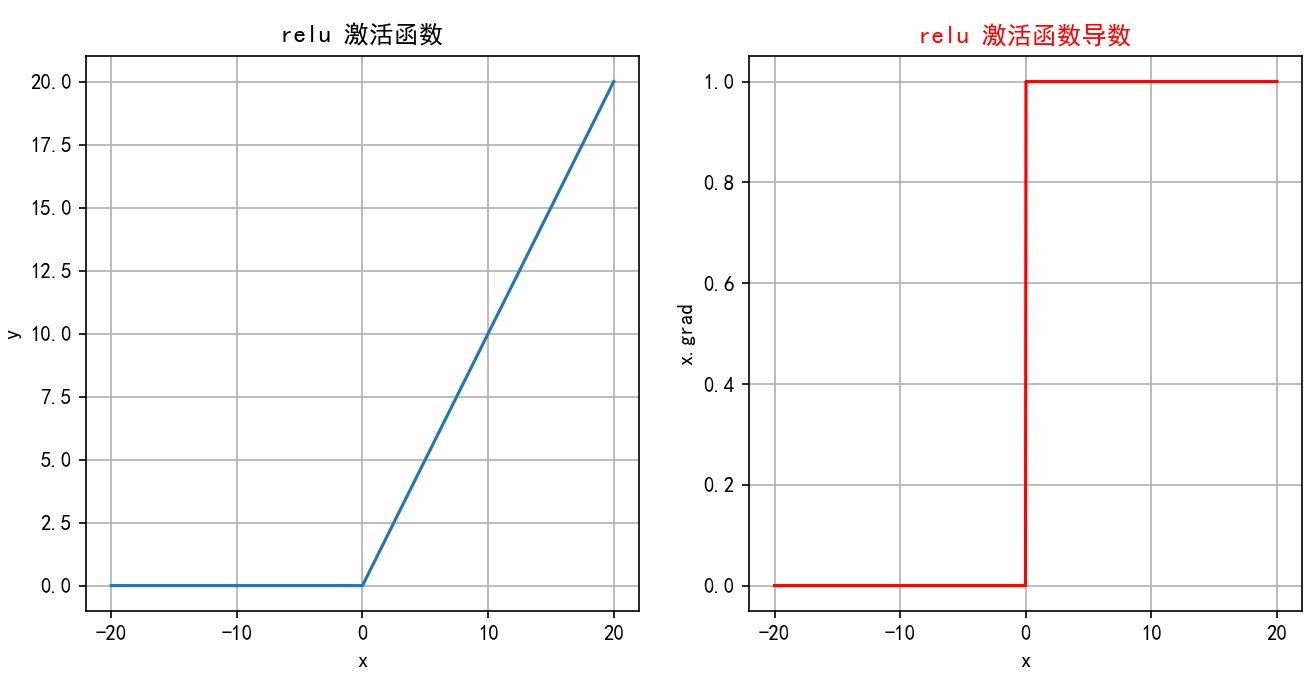
图像是一个简单的折线:在原点(0,0)左侧是水平线(y=0),在原点右侧是一条45度角的直线(y=x)。导数图像:在x<0处是y=0的水平线;在x>0处是y=1的水平线;在x=0处不连续(通常画一个空心点)。
-
4. Leaky ReLU (LReLU)
-
公式:
(其中
α是一个很小的正数常数,如0.01) -
原理: 针对标准ReLU的“死亡”问题进行的改进。在负区间给予一个很小的非零斜率
α。 -
特征:
-
输出范围: (-∞, +∞) (理论上,但负值部分很小)
-
缓解死亡ReLU: 在负区间有小的梯度
α,(x<0)时输出(\alpha x)(非零),即使输入为负,神经元也有机会更新权重,避免了永久性“死亡”。 -
计算高效: 和ReLU一样高效。
-
-
缺点:
-
效果依赖
α: 需要人工设定或尝试α值。虽然通常设0.01有效,但并非最优。 -
在
x=0处不可导: 同样的问题。 -
负区间表现可能不一致: 微小的负斜率可能不足以完全解决某些场景下的问题,或者引入不必要的复杂性。
-
-
函数绘制:
-
当
x >= 0时,LReLU(x) = x(沿y=x直线在第一象限)。 -
当
x < 0时,LReLU(x) = αx(一条斜率为α的直线,在第三象限,非常平缓)。 -
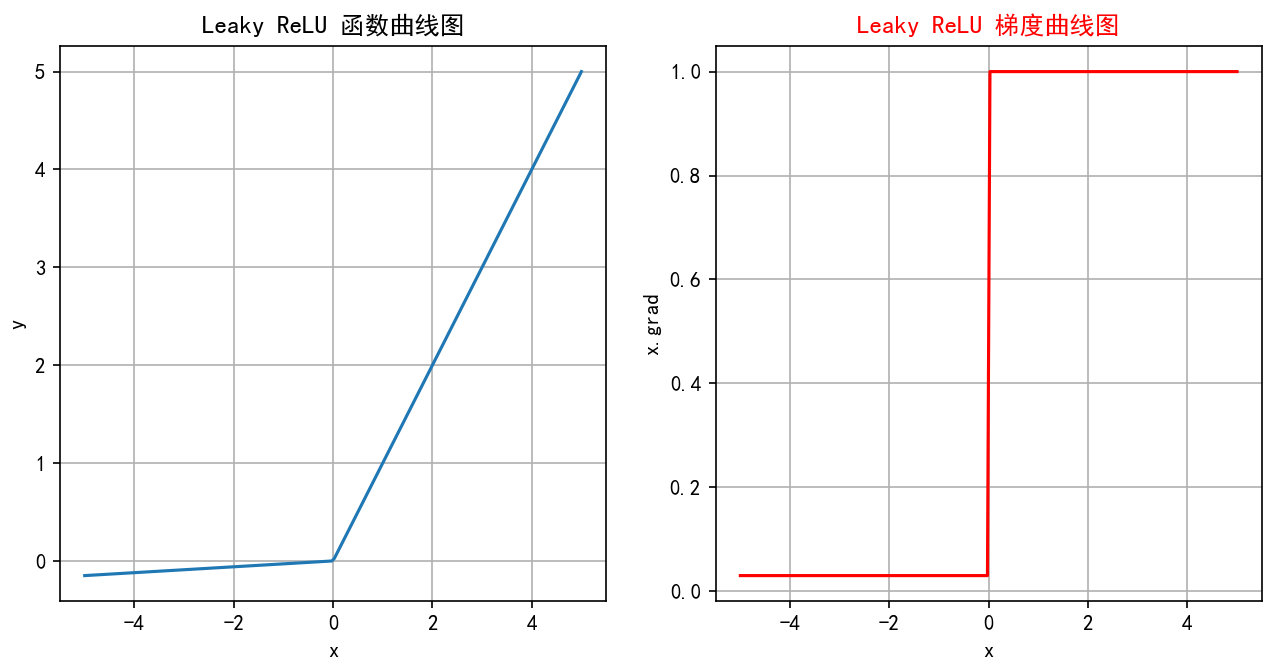
图像在原点右侧与ReLU相同(y=x),在原点左侧是一条斜率很小(接近水平)的直线。导数图像:在x>0处是y=1的水平线;在x<0处是y=α的水平线(非常接近0);在x=0处不连续。
-
5. Softmax
-
公式:
(其中
是第i个神经元的输入,K是输出层神经元的个数/类别数)
给定输入向量 z=[
,
,…,
]
1.指数变换:对每个
进行指数变换,得到
,使z的取值区间从
变为
2.将所有指数变换后的值求和,得到
3.将t中每个
除以归一化因子s,得到概率分布:
即:
-
原理: 将多个神经元的输入(通常是一个向量
z = [z1, z2, ..., zK])转换为一个概率分布。每个输出值在(0, 1)区间,且所有输出值之和为1,适合作为多分类任务的输出层。 -
特征:
-
输出范围: (0, 1)
-
归一化: 输出总和为1,非常适合表示K个互斥类别的概率分布(多分类问题)。
-
放大差异: 输入值中最大的那个,其对应的输出概率会被显著放大(指数效应),较小的输入对应的概率会被压缩。
-
在实际应用中,Softmax常与交叉熵损失函数Cross-Entropy Loss结合使用,用于多分类问题。在反向传播中,Softmax的导数计算是必需的。
-
-
缺点:
-
仅用于输出层: 通常只在多分类网络的最后一层使用。
-
梯度消失:当某个输入远大于其他时,其对应的输出趋近于 1,其他趋近于 0,梯度接近 0。
-
API
torch.nn.functional.softmax
import torch
import torch.nn as nn
# 表示4分类,每个样本全连接后得到4个得分,下面示例模拟的是两个样本的得分
input_tensor = torch.tensor([[-1.0, 2.0, -3.0, 4.0], [-2, 3, -3, 9]])
softmax = nn.Softmax()
output_tensor = softmax(input_tensor)
# 关闭科学计数法
torch.set_printoptions(sci_mode=False)
print("输入张量:", input_tensor)
print("输出张量:", output_tensor)
输出结果:
输入张量: tensor([[-1., 2., -3., 4.],[-2., 3., -3., 9.]])
输出张量: tensor([[ 0.0059, 0.1184, 0.0008, 0.8749],[ 0.0000, 0.0025, 0.0000, 0.9975]])总结对比表
| 激活函数 | 公式 | 输出范围 | 优点 | 缺点 | 适用场景 | 函数绘制描述 |
|---|---|---|---|---|---|---|
| Sigmoid | (0, 1) | 平滑,输出可解释为概率,导数易求 | 梯度消失严重,输出非零中心,计算慢 | 二分类输出层,早期隐藏层 | S形曲线,从(0,0)附近到(0,1)附近,关于(0,0.5)对称 | |
| Tanh | (-1, 1) | 零中心化,梯度比Sigmoid稍大 | 仍有梯度消失,计算慢 | 隐藏层(比Sigmoid更常用) | S形曲线,从(0,-1)附近到(0,1)附近,关于(0,0)对称 | |
| ReLU | max(0, x) | [0, +∞) | 计算极快,有效缓解梯度消失(正区间),生物学启发,实践效果好 | 死亡ReLU问题,输出非零中心,x=0不可导 | 最常用隐藏层 (CNN, FNN) | x<0为水平线(y=0),x>=0为45度线(y=x),原点处转折 |
| Leaky ReLU | | (-∞, +∞) | 缓解死亡ReLU,计算快 | 效果依赖α,x=0不可导,负斜率可能非最优 | 隐藏层 (ReLU的改进尝试) | x>=0同ReLU(y=x),x<0为斜率很小的直线(y=αx) |
| Softmax | (0, 1), Σ=1 | 输出归一化为概率分布,适合多分类 | 仅用于输出层,数值不稳定(需技巧) | 多分类输出层 | 作用于向量,输出概率向量。最大输入对应最大概率(接近1) |
损失函数选择
-
隐藏层:优先用ReLU,计算快、效果稳。若出现大量 “死神经元”(输出恒为 0),换Leaky ReLU
-
输出层:
-
二分类: Sigmoid (输出单个概率)。
-
多分类: Softmax (输出类别概率分布)。
-
回归:
-
输出非负(如销量):ReLU
-
输出可正可负(如温度):线性激活(y=x) 或Tanh(配合缩放)
-
-
循环网络(RNN/LSTM):门控用Sigmoid(控制开关),状态用Tanh(限制范围)。
-
-
避免使用: 在深度网络的隐藏层中,通常避免使用Sigmoid(梯度消失问题严重),也较少使用原始Tanh(ReLU族通常更优)。
