当前位置：首页 > news >正文

【MATLAB例程】基于UKF的IMM例程，模型使用CA（匀加速）和CT（协调转弯）双模型，二维环境下的轨迹定位。附代码下载链接

news 2025/8/10 8:38:19

在这里插入图片描述

本文介绍的MATLAB程序可以实现：基于交互式多模型（IMM）的无迹卡尔曼滤波（UKF）方法，用于二维平面中目标的运动状态估计。该算法结合了两个运动模型：匀速直线模型（CV）和匀速转弯模型（CT），可在不同运动模式间自适应切换，从而提高目标跟踪精度。

文章目录

程序详解
- 🧠 程序核心思想
- 📊 主要功能模块
运行结果
MATLAB源代码

程序详解

🧠 程序核心思想

在目标跟踪问题中，由于目标可能存在不同的运动模式（如直线、转弯等），单一模型很难始终适应。IMM算法通过在多个运动模型间加权融合预测结果，并实时调整模型权重，提升整体滤波鲁棒性和精度。

在每一步滤波中，IMM流程如下：

模型交互（混合）：基于前一时刻模型概率和转移矩阵计算混合初始状态。
状态预测：每个模型独立进行 UKF 预测。
观测更新：每个模型基于当前观测进行 UKF 校正，得到各自的状态估计和置信度。
模型概率更新：根据每个模型的观测匹配程度（似然）更新模型概率。
估计融合：加权融合所有模型的状态估计，得到当前最终估计值。

📊 主要功能模块

模拟真实轨迹
单模型 UKF 滤波
IMM UKF 滤波

运行结果

轨迹真值与不同方法得到的对比：
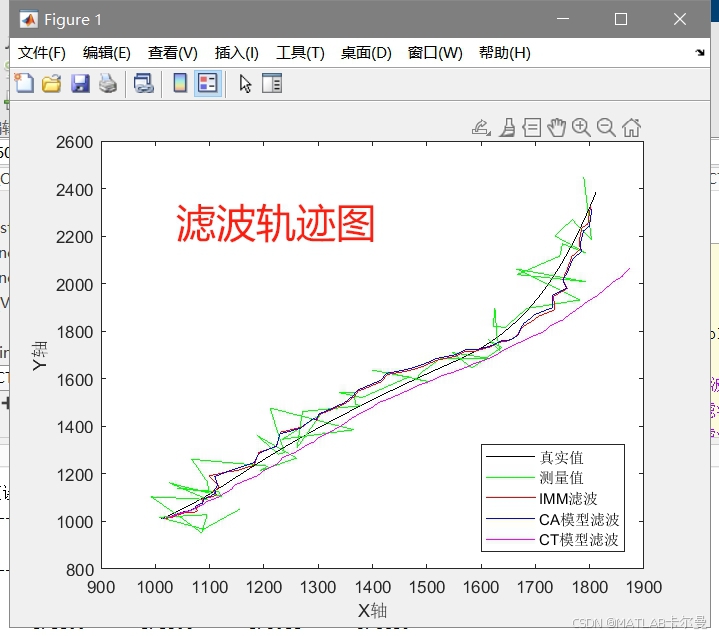
在这里插入图片描述

位置误差对比曲线：
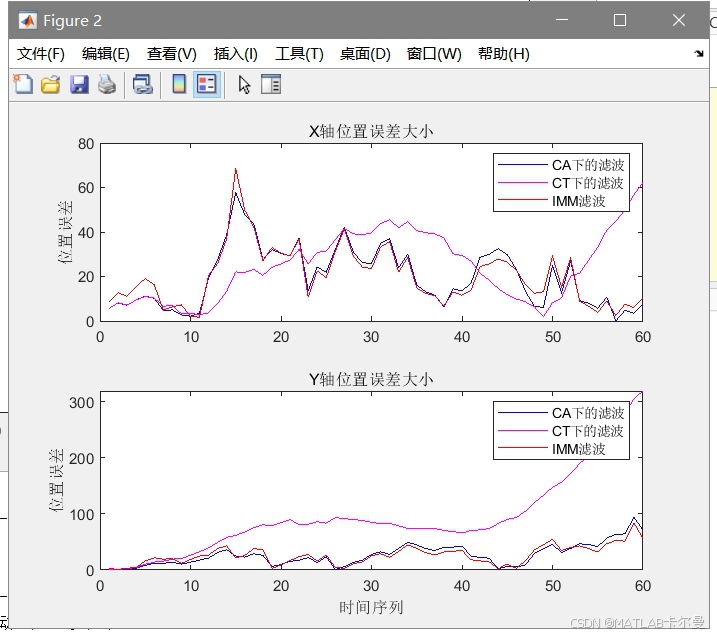
在这里插入图片描述

速度误差对比曲线：
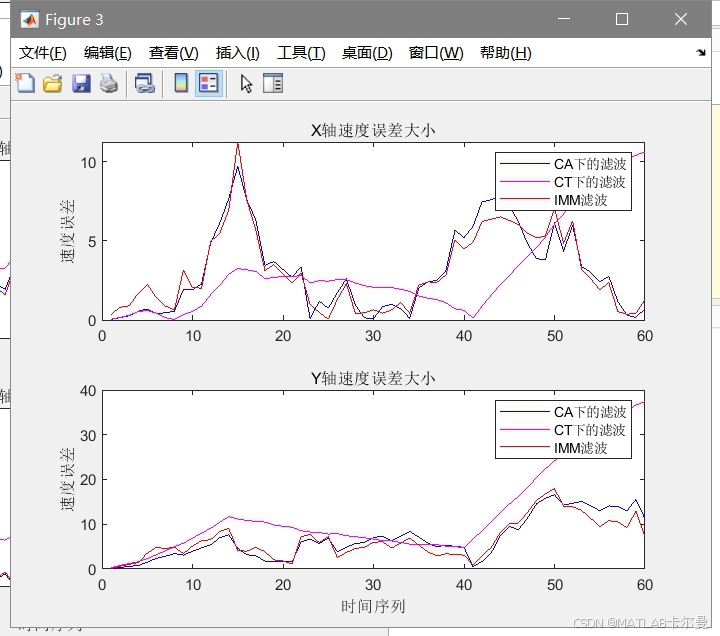
在这里插入图片描述

模型的概率曲线：
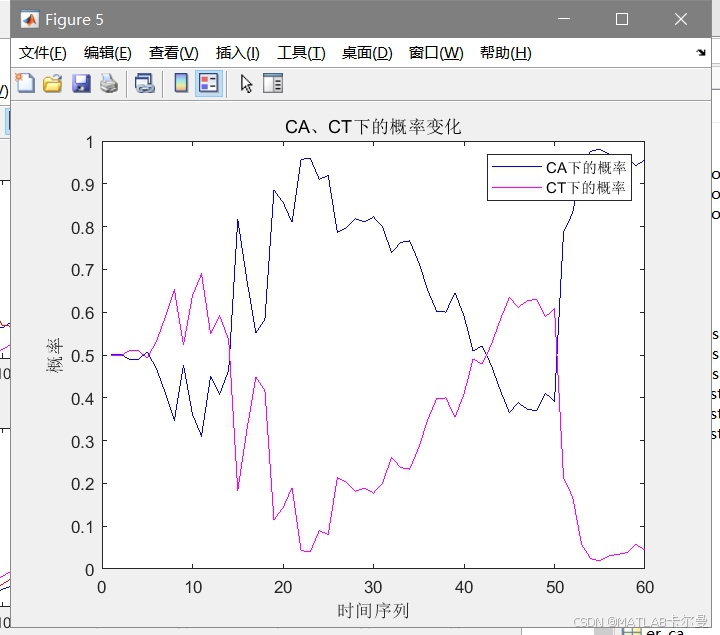
在这里插入图片描述

命令行窗口输出的误差统计特性对比：
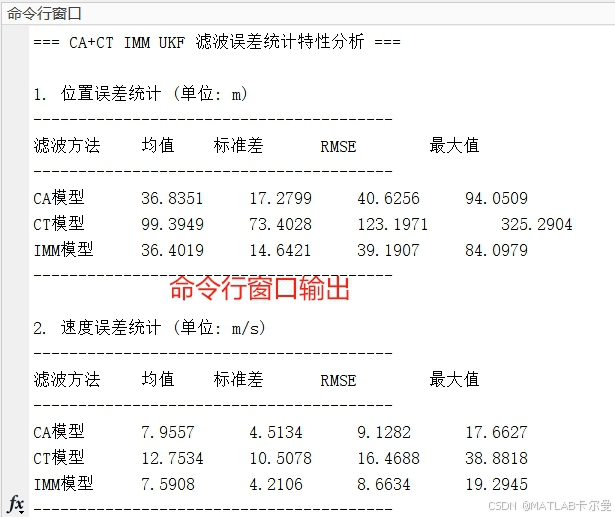
在这里插入图片描述

MATLAB源代码

部分代码如下：

% CV和CT模型组成的IMM UKF
% 2024-11-06/Ver1
% 2025-08-07/Ver2：添加误差统计特性计算与输出、优化非线性情况下的权重更新
%% 建模
clear; %清空工作区
clc; %清空命令行
close all; %关闭所有窗口（主窗口除外）
rng(0); %固定随机种子，让每次运行得到的结果相同
N = 600; %定义仿真时间为600
T = 1; %定义采样间隔为1
x0 = [1000,10,1000,10]'; %状态初始化，四项为别为x轴位置、速度、y轴位置、速度
xA = []; %预定义输出的状态
% CV匀速运动
% x = A1*x + G1*sqrt(Q1)*[randn,randn]';
A1 = [1,T,0,0;0,1,0,0;0,0,1,T;0,0,0,1]; %定义匀速运动时的状态转移矩阵
G1=[T^2/2,0;T,0;0,T^2/2;0,T] ; %设置匀速运动时的输入向量转移矩阵
Q1=0.01*diag([1,1]); %设置状态转移协方差矩阵
% CT匀速圆周运动
A2=CreatCTF(-pi/360,T); %设置匀速圆周运动时的状态转移矩阵
G2=CreatCTT(T); %设置匀速圆周运动时的输入向量转移矩阵
Q2=0.144^2*diag([1,1]); %设置匀速圆周运动时的% 产生真实数据
x = x0; %在迭代产生真值前，给x赋初值
for k = 1:140%匀速直线x = A1*x + G1*sqrt(Q1)*randn(size(Q1,1),1); %状态一步转移，后面的是误差xA =[xA x]; % 将迭代得到的x加在xA后面一列
end
for k = 1:260%匀速圆周转弯x = A2*x + G2*sqrt(Q2)*randn(size(Q2,1),1); %状态一步转移，后面的是误差xA =[xA x]; % 将迭代得到的x加在xA后面一列
end
for k = 1:N-400%匀速直线x = A1*x + G1*sqrt(Q1)*randn(size(Q1,1),1); %状态一步转移，后面的是误差xA =[xA x]; % 将迭代得到的x加在xA后面一列
end