数据结构与算法：树状数组

前言

太难了……

一、树状数组使用场景

树状数组一般用来维护可差分的信息，比如累加和，累乘积等。举个例子，当整个数组的累加和为sum1，一个区间内的累加和为sum2，那么除了这个区间剩下部分的累加和就是sum1-sum2，这就是可差分的信息。

不可差分的信息，如最大值和最小值，一般用线段树来维护。线段树虽然几乎可以完全替代树状数组，但代码量较多，常数时间比较大。

二、树状数组常见用法

1.一维数组上单点增加、范围查询

（1）原理详解

虽然单点增加直接在原数组上操作即可，但对于范围查询，以现有的知识，肯定就是构建前缀和数组，然后每次输出范围累加和即可。但每次单点增加时，都需要从这个点开始遍历前缀和数组到结尾，把每个位置都加上这个增加的数，那这样的时间复杂度就很高了。

树状数组可以实现每次单点增加和范围查询的时间复杂度均为O(logn)，这个复杂度相比每次都遍历的O(n)要优秀太多了。

首先要铭记！树状数组的下标必须以1开始！树状数组的所有操作都是基于这一点的！

接着，先将数组按上图方式从左到右划分原数组。方法就是，首先规定每个区间的长度为2的幂，那么最小的区间长度就是2的0次方，即1长度，之后长度每次乘以2。那么以1长度的区间划分数组的话，每个区间里就只有自己那个位置的数，可以将数组划分成数组长度个区间。之后以2长度划分，所以每个区间里就有两个数，比如第一个区间里是1位置和2位置两个数，第二个区间里是3位置和4位置的数。之后一直到16长度，即整个数组都在这个区间内。注意，区间要一直增长到能把整个数组包住，数组长度不够了不要紧。

之后，树状数组index-tree[i]的定义是，原数组中以i为右边界，最长的一个区间的累加和。那么1位置的值就是原数组中以1位置为右边界的最长区间，那就是1位置自己，所以值为1。之后2位置的值就是原数组中以2位置有右边界的最长区间，那么就是长度为2的区间，包括1位置和2位置，所以值就是2。之后4位置的值包括1到4位置，所以就是4。还有12位置就是原数组中以12为右边界的最长区间，那么就是长度为4，包括9~12位置的区间，所以值也是4。之后以此类推8位置就是8,16位置就是16。

所以，树状数组中，i位置负责的区间包括的范围的左边界，就是i这个数去掉自己二进制的最右的1后再加1。举个例子，12的二进制为1100，去掉最右的1就是1000，再加1就是1001，对应的十进制数就是9，所以tree[12]负责的区间就是9~12，和上面的定义一致。

（别看上图写的，估计当时脑子抽了笔误了）

之后，如果要求原数组1~i范围上的累加和，那么先加上树状数组中i位置的值，再移除这个i的最右侧的1，然后加上移除后的i位置的值，直到i等于0。

举个例子，假如要求原数组1~15范围上的前缀和，那么就是先加上tree[15]，即原数组15~15范围上的数的累加和。再移除15最右侧的1，变成14，然后加上tree[14]，即原数组13~14范围上的数的累加和。再移除14最右侧的1变成12，然后加上tree[12]，即原数组9~12范围上的数的累加和。再移除12最右侧的1变成8，然后加上tree[8]，即原数组1~8范围上的数的累加和。此时再移除最右侧的1就变成0了，所以停止。可以发现，这样加下来正好是1~15范围上的数的累加和。

对于单点增加的操作，就需要在树状数组中所有包括该点的区间的位置上全进行增加。方法是，如果要在原数组的i位置增加v，那么先在树状数组中的i位置增加v，因为必然包括i这个位置。之后每次让i加上自己最右侧的1，然后在新的i位置增加v，直到i越界。

举个例子，假如要在原数组的11位置增加3，那么就是先在tree[11]上加3。然后由于11的二进制为01011，所以加上最右侧的1变成01100，即12，那么就在tree[12]上加3。然后再加上最右侧的1变成10000，即16，那么就在tree[16]上加3，之后越界停止。可以发现，原数组的11位置，被且只被tree[11]，tree[12]，tree[16]代表的区间包括。

所以对于范围查询的操作，只需要用1~r范围上的累加和减去1~l-1范围上的累加和即可。

（2）模板——树状数组 1

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=5e5+5;
int n,m;//树状数组
vector<int>tree(MAXN);//提取最右侧1
int lowbit(int i)
{return i&-i;
}//加
void add(int i,int v)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}//1~i累加和
int sum(int i)
{int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//范围查询
int query(int l,int r)
{return sum(r)-sum(l-1);
}void solve()
{cin>>n>>m;//利用add方法建树状数组for(int i=1,v;i<=n;i++){cin>>v;add(i,v);}for(int i=0,type;i<m;i++){cin>>type;if(type==1){int x,k;cin>>x>>k;add(x,k);}else{int l,r;cin>>l>>r;cout<<query(l,r)<<endl;}}}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

树状数组虽然原理挺难的，但代码其实很简单。

首先是lowbit函数负责求i这个数最右侧的1，直接i&(-i)即可。

之后是add函数，只要i小于等于n，即没越界，那就每次让tree[i]加上v，然后i增加lowbit(i)即可。

sum函数负责返回原数组1~i范围上的数的累加和，那就是只要i大于0，每次让ans加上tree[i]，然后i减去lowbit(i)，最后返回ans即可。

所以query范围查询只需要返回sum(r)-sum(l-1)即可。

既然有了add方法，一开始构建树状数组的时候直接调用就行了。

2.一维数组上范围增加、单点查询

（1）原理详解

范围增加就需要一点思考了。

首先，原数组arr的差分数组D[i]的定义是arr[i]-arr[i-1]，所以arr[i]就是差分数组D从1~i的前缀和。之后，不对原数组构建树状数组，而是对原数组的差分数组D构建树状数组。所以单点查询就是求差分数组1~i的前缀和，那直接调用sum方法就行了。对于范围增加，那就和一维差分一样，在差分数组的l位置加上v，在r+1位置减去v，那直接调用两次原本的add方法即可。

（2）模板——树状数组 2

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=500000+5;//树状数组 -> 维护差分数组
vector<int>tree(MAXN);
int n,m;int lowbit(int i)
{return i&-i;
}//原始add
void add(int i,int v)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}int sum(int i)
{int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//新add
void add(int l,int r,int v)
{add(l,v);add(r+1,-v);
}//新query
int query(int i)
{return sum(i);
}void solve()
{cin>>n>>m;for(int i=1,v;i<=n;i++){cin>>v;add(i,i,v);}for(int i=0,type;i<m;i++){cin>>type;if(type==1){int l,r,v;cin>>l>>r>>v;add(l,r,v);}else{int x;cin>>x;cout<<query(x)<<endl;}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

代码没啥好说的，和上面描述的一样。

3.一维数组上范围增加、范围查询

这个就已经到了线段树的领域了。

（1）原理详解

首先先考虑原数组1~k范围上的累加和的求法，如果有了这个方法那么范围查询的事就解决了。还是考虑引入差分数组，那么就可以将原数组的累加和转化成差分数组的累加和。之后合并可得，一共需要加k个D[1]，k-1个D[2]，一直到k-(k-1)，即1个D[k]，那么再提取出k并写成数学表达式就是如上图所示。因为有两个未知量，所以考虑构建两个树状数组分别维护原始差分数组和(i-1)D[i]这个新数组。

（2）模板——线段树 1

byd抽象起来了。

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=1e5+5;//维护差分数组
vector<ll>tree1(MAXN);
//维护(i-1)*Di数组
vector<ll>tree2(MAXN);int n,m;int lowbit(int i)
{return i&-i;
}//原始add，告诉在哪棵树上add
void add(vector<ll>&tree,int i,ll v)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}//原始1~i的累加和
ll sum(vector<ll>&tree,int i)
{ll ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//原数组中[l……r]+v
void add(int l,int r,ll v)
{add(tree1,l,v);add(tree1,r+1,-v);add(tree2,l,(l-1)*v);add(tree2,r+1,-r*v);
}//1~k的累加和
ll query(int k)
{return k*sum(tree1,k)-sum(tree2,k);
}//原数组范围累加和
ll query(int l,int r)
{return query(r)-query(l-1);
}void solve()
{cin>>n>>m;for(int i=1;i<=n;i++){ll v;cin>>v;add(i,i,v);}for(int i=0,type;i<m;i++){cin>>type;if(type==1){ll l,r,v;cin>>l>>r>>v;add(l,r,v);}else{int l,r;cin>>l>>r;cout<<query(l,r)<<endl;}}    
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

代码就是完全根据上面思路写的，就是几个函数套函数实现的。

原数组范围累加和就是调用两次原数组1~k范围累加和，原数组1~k范围累加和再使用公式计算，那还需要调用两个树状数组维护的差分数组1~k上的累加和。然后每次范围增加都要分别调用两次两个树状数组的单点增加。

4.二维数组上单点增加、范围查询

二维的题不管是用树状数组还是线段树都很难，所以基本很少见。

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;//二维树状数组
vector<vector<int>>tree;int n,m;int lowbit(int i)
{return i&-i;
}//单点增加 -> O(logn*logm)
void add(int x,int y,int v)
{for(int i=x;i<=n;i+=lowbit(i)){for(int j=y;j<=m;j+=lowbit(j)){tree[i][j]+=v;}}
}//(1,1)->(x,y)的累加和
int sum(int x,int y)
{int ans=0;for(int i=x;i>0;i-=lowbit(i)){for(int j=y;j>0;j-=lowbit(j)){ans+=tree[i][j];}}return ans;
}//范围查询
int query(int a,int b,int c,int d)
{//二维差分return sum(c,d)-sum(a-1,d)-sum(c,b-1)+sum(a-1,b-1);
}void solve()
{cout<<"VIP题,没法做,所以就只有代码了……"<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

二维数组的单点增加和范围查询基本和二维差分一样，就是构建二维树状数组维护二维差分数组。然后单点增加和一维的单点增加类似，是两个循环嵌套。然后(1,1)到(x,y)范围上的累加和也和一维的类似，范围查询就是二维前缀和数组求范围累加和的公式。

5.二维数组上范围增加、范围查询

太抽象了……

（1）原理详解

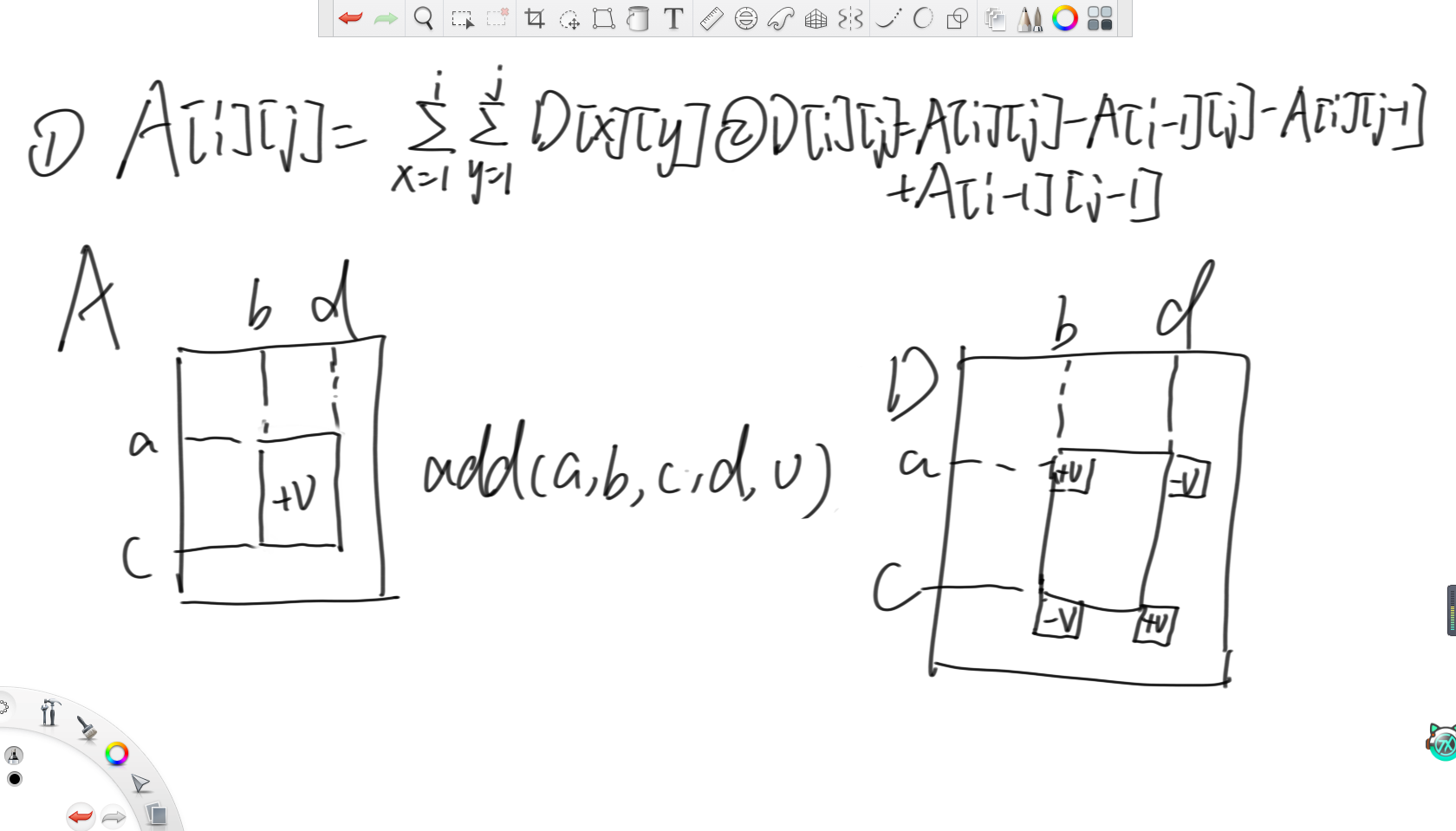
二维数组上的范围增加还是利用二维差分数组，根据二维差分可得，原数组上A[i][j]的值就是差分数组从(1,1)一直求和到(i,j)，差分数组D[i][j]的值就是原数组这个位置的值减去上方格子，左侧格子和左上格子。

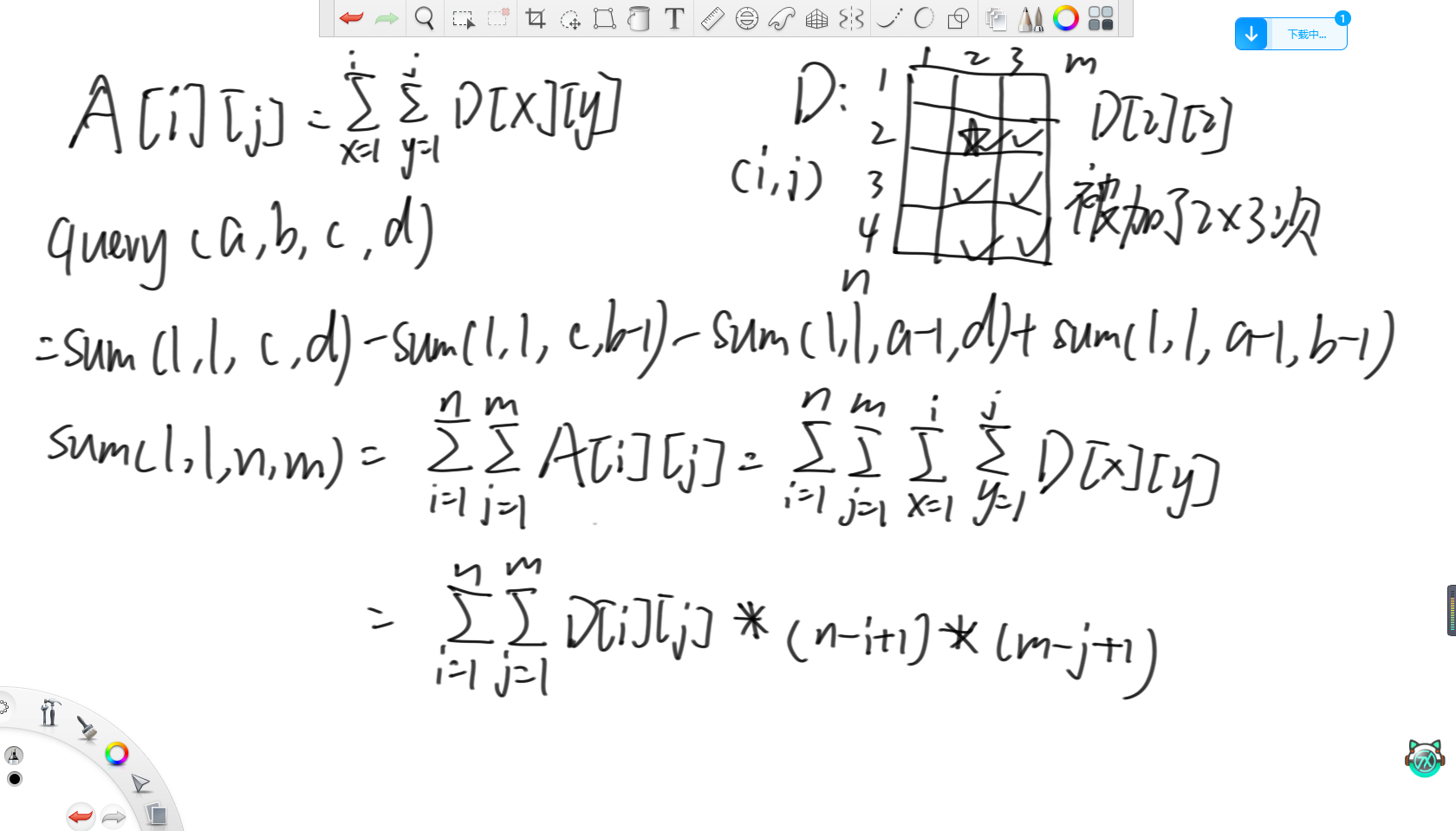
根据二维前缀和，原数组的范围查询就要调用四次二维前缀和，所以解决求(1,1)到(n,m)累加和的问题就可以了。那么就需要考虑如何在差分数组中求累加和，所以可以得到这个四层循环嵌套的形式，之后肯定需要对其进行化简。观察上述例子，在求(1,1)到(4,3)的过程中，D[2][2]一共被加了2*3=6次，即当(i,j)来到(2,2)到(4,3)这个范围内时才会把这个格子加一遍。所以这个四层循环的公式可以化简为只和(i,j)有关的最终形式。

再将这个最终形式化简，就可以得到如上的形式，所以就需要用四个树状数组分别维护这四个信息。每次增加都对这四个差分数组进行操作。

（2）模板——上帝造题的七分钟

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=2048+5;
const int MAXM=2048+5;int n,m;//D[i][j]的树状数组
vector<vector<int>>tree1(MAXN,vector<int>(MAXM));
//D[i][j]*i的树状数组
vector<vector<int>>tree2(MAXN,vector<int>(MAXM));
//D[i][j]*j的树状数组
vector<vector<int>>tree3(MAXN,vector<int>(MAXM));
//D[i][j]*i*j的树状数组
vector<vector<int>>tree4(MAXN,vector<int>(MAXM));int lowbit(int i)
{return i&-i;
}//单点增加
void add(int x,int y,int v)
{int v1=v;int v2=x*v;int v3=y*v;int v4=x*y*v;for(int i=x;i<=n;i+=lowbit(i)){for(int j=y;j<=m;j+=lowbit(j)){tree1[i][j]+=v1;tree2[i][j]+=v2;tree3[i][j]+=v3;tree4[i][j]+=v4;}}
}//(1,1)->(x,y)求和
int sum(int x,int y)
{int ans=0;for(int i=x;i>0;i-=lowbit(i)){for(int j=y;j>0;j-=lowbit(j)){ans+=(x+1)*(y+1)*tree1[i][j]-(y+1)*tree2[i][j]-(x+1)*tree3[i][j]+tree4[i][j];}}return ans;
}//范围增加
void add(int a,int b,int c,int d,int v)
{add(a,b,v);add(a,d+1,-v);add(c+1,b,-v);add(c+1,d+1,v);
}//范围查询
int query(int a,int b,int c,int d)
{return sum(c,d)-sum(a-1,d)-sum(c,b-1)+sum(a-1,b-1);
}void solve()
{char type;int a,b,c,d,v;//一直读取直到结尾while(scanf("%s",&type)!=EOF)//不能用%c -> 避免读取回车或空格字符！{if(type=='X'){scanf("%d %d",&n,&m);}else if(type=='L'){scanf("%d %d %d %d %d",&a,&b,&c,&d,&v);add(a,b,c,d,v);}else{scanf("%d %d %d %d",&a,&b,&c,&d);printf("%d\n",query(a,b,c,d));}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

所以每次范围增加时，要根据二维差分调用四次单点增加的函数，然后在单点增加的函数里，要先求出四个数组分别增加的值，然后循环增加四个数组的值。范围查询时就要根据二维前缀和调用四次从(1,1)到(n,m)的前缀和，然后在前缀和的函数里就是按照公式计算即可。

三、题目

1.逆序对

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=5e5+5;
vector<ll>arr(MAXN);
vector<ll>help(MAXN);//归并排序辅助数组//归并排序+合并左右答案
ll merge(int l,int m,int r)
{//统计答案ll ans=0;//i和j分别从左侧和右侧的最右位置开始for(int i=m,j=r;i>=l;i--){while(j>=m+1&&arr[i]<=arr[j]){j--;}//j右侧均为可以和a[i]构成逆序对的数ans+=j-m;}//归并排序int i=l;//填的位置//左右部分指针int a=l;int b=m+1;while(a<=m&&b<=r){help[i++]=arr[a]<=arr[b]?arr[a++]:arr[b++];}//填剩余的while(a<=m){help[i++]=arr[a++];}while(b<=r){help[i++]=arr[b++];}//重设arrfor(int i=l;i<=r;i++){arr[i]=help[i];}return ans;
}//l~r范围上的逆序对数量
ll dfs(int l,int r)
{if(l==r){return 0;}int m=(l+r)/2;return dfs(l,m)+dfs(m+1,r)+merge(l,m,r);
}//归并分治解
void solve1()
{int n;cin>>n;for(int i=0;i<n;i++){cin>>arr[i];}cout<<dfs(0,n-1)<<endl;
}//树状数组
vector<int>tree(MAXN);int lowbit(int i)
{return i&-i;
}void add(int i,int v,int n)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}//1~i的累加和
ll sum(int i)
{ll ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}//查出现位置
int bs(int i,int m,vector<ll>&sorted)
{int l=1;int r=m;int mid;int ans=0;while(l<=r){mid=(l+r)/2;if(sorted[mid]>=i){ans=mid;r=mid-1;}else{l=mid+1;}}return ans;
}//树状数组解
void solve2()
{int n;cin>>n;for(int i=1;i<=n;i++){cin>>arr[i];}//树状数组维护词频数组//然后从后往前遍历，边统计词频边统计答案//此时，树状数组的下标为数值 -> 值域树状数组//因为数字很大，所以要对其离散化vector<ll>sorted(n+1);for(int i=1;i<=n;i++){sorted[i]=arr[i];}sort(sorted.begin()+1,sorted.end());//去重int m=1;for(int i=2;i<=n;i++){if(sorted[m]!=sorted[i]){sorted[++m]=sorted[i];}}//二分for(int i=1;i<=n;i++){arr[i]=bs(arr[i],m,sorted);}//构建树状数组ll ans=0;for(int i=n;i>=1;i--){ans+=sum(arr[i]-1);add(arr[i],1,m);}cout<<ans;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve2();    }return 0;
}

这个题有归并分治和树状数组两个解。归并分治的解比较好理解，但缺点是只能离线处理，没法在线处理。树状数组的解虽然比较难想，但可以支持在线查询。

归并分治的解就比较好理解了，只需要在每次merge的过程中，设置双指针滑一遍两部分就能统计出答案，然后进行归并排序即可。

代码就是dfs返回l到r范围上的逆序对数量，然后在merge的过程中，分别在左侧和右侧的最右位置设置两个指针，只要右指针位置的数大于等于左指针位置的数，就让右指针左移。由于归并排序保证了左右两侧分别有序，所以此时从右指针到中间的所有数都小于左指针位置的数。所以此时左指针位置的数对答案的贡献就是右指针到中间的数的个数。遍历完一遍后归并排序整合左右两侧即可。

树状数组的解比较需要思考了，这里考虑用树状数组维护词频数组。之后，考虑从后往前遍历，每个数对答案的贡献就是此时词频表中小于这个数的个数，那么就可以用树状数组实现在线查询了。

要注意的是，由于树状数组维护的是词频表，所以下标代表的是实际数字，所以如果直接开整个数字范围的长度，有可能导致空间过大。所以要考虑对数组进行离散化，方法是设置一个sorted数组，先把原数组抄过来，然后对其进行排序。之后，设置双指针对排序后的数组进行去重，只提取数字的种类。最后，利用这个去重后的sorted数组，将原数组映射成大小排名，所以就是每次在sorted数组有效部分里二分找相同的数字的位置，然后用这个位置作为这个数字大小的排名建立词频表。这样，就把规模由原来跟数字大小有关，转化成了跟原数组长度有关。

所以代码就是先把原数组抄到sorted数组里排序，接着进行去重。去重的方法就是设置m为有效区域的右边界，注意，由于这里的下标对应树状数组的下标，所以m要从1开始计算。只要m位置的数不等于i位置的数，说明出现了一个不同的数，那就把m的下一个位置填成这个出现的新数。之后就是二分找原数组中的数的大小排名，再填回原数组。最后就是遍历原数组，每次统计当前数对答案的贡献，即小于等于当前数减一的词频之和。然后让当前数的词频加一，在树状数组中修改即可。

2.三元上升子序列

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=3e4+5;
const int MAXV=1e5+5;//词频表的树状数组
vector<ll>cnts(MAXV);
//上升二元组的树状数组
vector<ll>two(MAXV);int lowbit(int i)
{return i&(-i);
}void add(int i,ll v,vector<ll>&tree)
{while(i<MAXV){tree[i]+=v;i+=lowbit(i);}
}ll sum(int i,vector<ll>&tree)
{ll ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}void solve()
{int n;cin>>n;vector<ll>a(n+1);for(int i=1;i<=n;i++){cin>>a[i];}//建立词频表 -> 上升一元组数量//建立以v结尾的上升二元组数量 -> 词频表的前缀和//以v结尾的上升三元组数量 -> 上升二元组数量的前缀和ll ans=0;for(int i=1;i<=n;i++){ans+=sum(a[i]-1,two);add(a[i],1,cnts);add(a[i],sum(a[i]-1,cnts),two);}cout<<ans;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

这个题的思路跟上一道很类似，首先还是建立一个词频表，含义可以理解为上升一元组数量，所以每次就在对应的位置加一即可。然后再建立一个以v结尾的上升二元组数量的数组，所以这个上升二元组每次就加上小于这个数的词频总数。所以对于每个数，对答案的贡献就是上升二元组里小于这个数的个数。所以只需要分别对这个词频表和上升二元组建立两个树状数组，之后这些信息就都可以快速查询了。

3.最长递增子序列的个数

class Solution {
public:int MAXN=2000+5;//离散化vector<int>sorted;//结尾值<=i的最长递增子序列长度vector<int>treeMaxLen;//个数vector<int>treeMaxLenCnt;int m=0;int maxLen,maxLenCnt;void build(){sorted.resize(MAXN);treeMaxLen.resize(MAXN);treeMaxLenCnt.resize(MAXN);}int findNumberOfLIS(vector<int>& nums) {int n=nums.size();build();//树状数组维护以每个位置负责的数值结尾的情况下，//最长递增子序列的长度和个数//e.g.tree[4]维护以1~4结尾的最长长度和对应个数//遍历时更新 -> 按lowbit跳转add//每次统计最长的个数 -> 按lowbit跳转sum//离散化for(int i=1;i<=n;i++){sorted[i]=nums[i-1];}sort(sorted.begin()+1,sorted.begin()+n+1);m=1;for(int i=2;i<=n;i++){if(sorted[m]!=sorted[i]){sorted[++m]=sorted[i];}}//统计答案for(int num:nums){int i=rank(num);//查询query(i-1);//之前的最大长度再往上冲一个//若之前的个数为0，说明只有自己，当前个数为1add(i,maxLen+1,max(maxLenCnt,1));}//m为最大值 -> 找以所有数值结尾的答案 -> 整体最长递增子序列个数query(m);return maxLenCnt;}int lowbit(int i){return i&(-i);}//更新以<=i结尾的最长递增子序列的长度和个数void add(int i,int len,int cnt){while(i<=m){if(treeMaxLen[i]==len)//没法冲得更长{treeMaxLenCnt[i]+=cnt;}else if(treeMaxLen[i]<len)//能冲得更长{treeMaxLen[i]=len;treeMaxLenCnt[i]=cnt;}i+=lowbit(i);}}//查询以<=i结尾的最长递增子序列的长度和个数void query(int i){//全局变量返回两个值maxLen=maxLenCnt=0;while(i>0){if(maxLen==treeMaxLen[i])//没法冲得更长{maxLenCnt+=treeMaxLenCnt[i];}else if(maxLen<treeMaxLen[i])//能冲得更长{maxLen=treeMaxLen[i];maxLenCnt=treeMaxLenCnt[i];}i-=lowbit(i);}}//查询排名int rank(int v){int l=1;int r=m;int mid;int ans=0;while(l<=r){mid=(l+r)/2;if(sorted[mid]>=v){ans=mid;r=mid-1;}else{l=mid+1;}}return ans;}
};

这个题的思路也比较难想。

思路就是用两个树状数组分别维护以小于等于v这个数结尾的最长递增子序列的长度和个数。之后，每次查询或增加时， 都利用树状数组O(logn)的时间遍历1~i的方法，去根据lowbit跳转。

在查询时，因为要返回最长长度和对应个数两个值，所以考虑用全局变量实现。在跳转过程中，如果之前的值的最长递增子序列的长度等于当前的最长长度，那么此时的长度就要加上小于等于当前i的最长递增子序列的个数。如果当前的最长递增子序列的长度比目前的最长长度更长，那么当前的数就能踩在之前的最长递增子序列上更新得更长，所以就更新当前的maxLen和maxLenCnt即可。

查询完以小于当前数结尾的最长递增子序列的长度和个数后，当前数就可以踩在上面把这个长度更新得更长，那就是maxLen再加一。这里注意，如果查出来的个数为0，说明当前数只能自己一个，所以maxLenCnt还要和1取一个最大值。之后更新时，还是按lowbit跳转更新之前的maxLen和maxLenCnt。如果之前的长度等于len时，那么就没法借助当前数冲得更长，那就只增加个数。如果小于，那么说明可以变得更长，那就更新两个树状数组即可。

注意，由于这里树状数组的下标还是代表实际数字，所以还是需要对原数组进行离散化。

4.HH的项链

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
typedef pair<int,int> pii;
typedef pair<ll,ll>pll;const int MAXN=1e6+5;//树状数组维护区间内颜色出现的最右位置 -> 0：没出现过 1：出现过
vector<int>tree(MAXN);int lowbit(int i)
{return i&(-i);
}void add(int i,int v,int n)
{while(i<=n){tree[i]+=v;i+=lowbit(i);}
}int sum(int i)
{int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;
}int query(int l,int r)
{return sum(r)-sum(l-1);
}void solve()
{int n;scanf("%d",&n);vector<int>a(n+1);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}int m;scanf("%d",&m);vector<array<int,3>>q(m);for(int i=0;i<m;i++){scanf("%d%d",&q[i][0],&q[i][1]);q[i][2]=i;}//根据查询的右边界从小到大排序sort(q.begin(),q.end(),[&](const array<int,3>&x,const array<int,3>&y){return x[1]<y[1];});//map维护每种颜色出现的最右位置map<int,int>right;//答案vector<int>ans(m);for(int i=0,cur=1,l,r,fill;i<m;i++){//右边界r=q[i][1];//每次遍历到右边界for(;cur<=r;cur++){int color=a[cur];//该颜色以前出现过if(right[color]>0){//将旧位置上的标记去掉add(right[color],-1,n);}//在新位置标记add(cur,1,n);right[color]=cur;}l=q[i][0];fill=q[i][2];ans[fill]=query(l,r);}for(int i=0;i<m;i++){printf("%d\n",ans[i]);}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;//cin>>t;while(t--){solve();    }return 0;
}

nnd这题还必须用快读快写。

这题的思路也是很逆天了……首先，考虑对要查询的区间按右边界从小到大排序。但由于这会破坏原始查询的顺序，所以还要带着次序信息排序。之后，考虑建立一个map维护每种颜色出现的最右位置，再用树状数组维护一个区间内的颜色出现的最右位置。这里，tree[i]如果是1，就表示存在一种颜色的最右位置为i。

举个例子，假如此时的tree为[1,1,1,0]，而原数组为[3,1,2,3]，当前遍历到3位置。那么当来到4位置时，此时3号颜色最右出现的位置就不是1位置，而是4位置了。那么就需要将tree更新为[0,1,1,1]，表示当前不再存在一种颜色的最右位置为1位置。

所以就是遍历所有的查询，每次在原数组中遍历到当前查询的最右边界。在遍历原数组的过程中，如果当前颜色以前出现过，那么需要先在树状数组中把之前位置的1减去，然后在新位置打上标记。最后，只需要求当前查询区间的累加和就是其中不同的颜色的种类数。

这个思路的核心就是，通过只保留最右出现的位置，来实现同种颜色不重复统计。也是因为这一点，所以可以对查询的最右边界排序，这样在遍历原数组的过程中就能统计出答案。

5.得到回文串的最少操作次数

力扣的比赛这么逆天的吗……这题感觉没个几年的功力根本不可能写得出来……

class Solution {
public:const int MAXN=2000+5;//树状数组vector<int>tree;int n;//每个字符的出现位置 -> 链式前向星vector<int>ends;//最后出现的位置vector<int>pre;//之前出现的位置//每个字符应该去的位置vector<int>pos;//归并分治辅助数组vector<int>help;void build(){tree.resize(MAXN);pos.resize(MAXN);help.resize(MAXN);for(int i=1;i<=n;i++){//树状数组每个位置标记为1add(i,1);}ends.resize(26);pre.resize(MAXN);}int minMovesToMakePalindrome(string s) {n=s.length();build();//贪心：//从左往右遍历时，每次可以先满足当前位置的字符为回文//e.g. aaaabb -> a????a -> aa??aa -> aabbaa//关键：相邻交换！左侧往左交换过去时会把中间字符串挤过来//e.g. stXtYtYtXts -> 先满足X -> XsttYtYttsX -> XYstttttsYX -> (2+2)+(3+3)=10//                    先满足Y -> YstXtttXtsY -> YXstttttsYX -> (4+4)+(2+2)=12for(int i=0,j=1;i<n;i++,j++){//和树状数组有关，下标从1开始push(s[i]-'a',j);}for(int i=0,l=1,r,fill;i<n;i++,l++){//没分配位置if(pos[l]==0){//最后出现的位置r=pop(s[i]-'a');if(l<r)//这个字符剩不止一个{//应该去的位置fill=sum(l);pos[l]=fill;pos[r]=n-fill+1;//对称位置}else//只剩一个 -> 必在中间{pos[l]=(n+1)/2;}//去掉标签add(r,-1);}}//对pos求逆序对return number(1,n);}//统计字符出现位置void push(int v,int j){pre[j]=ends[v];ends[v]=j;}//每个字符的最后下标int pop(int v){int ans=ends[v];ends[v]=pre[ends[v]];return ans;}int lowbit(int i){return i&(-i);}void add(int i,int v){while(i<=n){tree[i]+=v;i+=lowbit(i);}}int sum(int i){int ans=0;while(i>0){ans+=tree[i];i-=lowbit(i);}return ans;}//归并分治求逆序对数量int number(int l,int r){if(l>=r){return 0;}int m=(l+r)/2;return number(l,m)+number(m+1,r)+merge(l,m,r);}//归并排序+合并左右答案int merge(int l,int m,int r){//统计答案int ans=0;//i和j分别从左侧和右侧的最右位置开始for(int i=m,j=r;i>=l;i--){while(j>=m+1&&pos[i]<=pos[j]){j--;}//j右侧均为可以和a[i]构成逆序对的数ans+=j-m;}//归并排序//填的位置int i=l;//左右部分指针int a=l;int b=m+1;while(a<=m&&b<=r){help[i++]=pos[a]<=pos[b]?pos[a++]:pos[b++];}//填剩余的while(a<=m){help[i++]=pos[a++];}while(b<=r){help[i++]=pos[b++];}//重设arrfor(int i=l;i<=r;i++){pos[i]=help[i];}return ans;}
};

这题的突破点其实需要贪心一下，那就是在从左往右遍历的过程中，可以先让当前来到的位置满足回文结构。举个例子，假如原串是aaaabb，那么在从左往右遍历时，可以先构成a????a，再构成aa??aa，最后aabbaa即可。具体原理如注释里写的，就是在左侧字符向左移动时，可以把左边的字符串挤过去，这样当更右侧的字符向左移动时，就不用经过那个已经移过去的字符了。

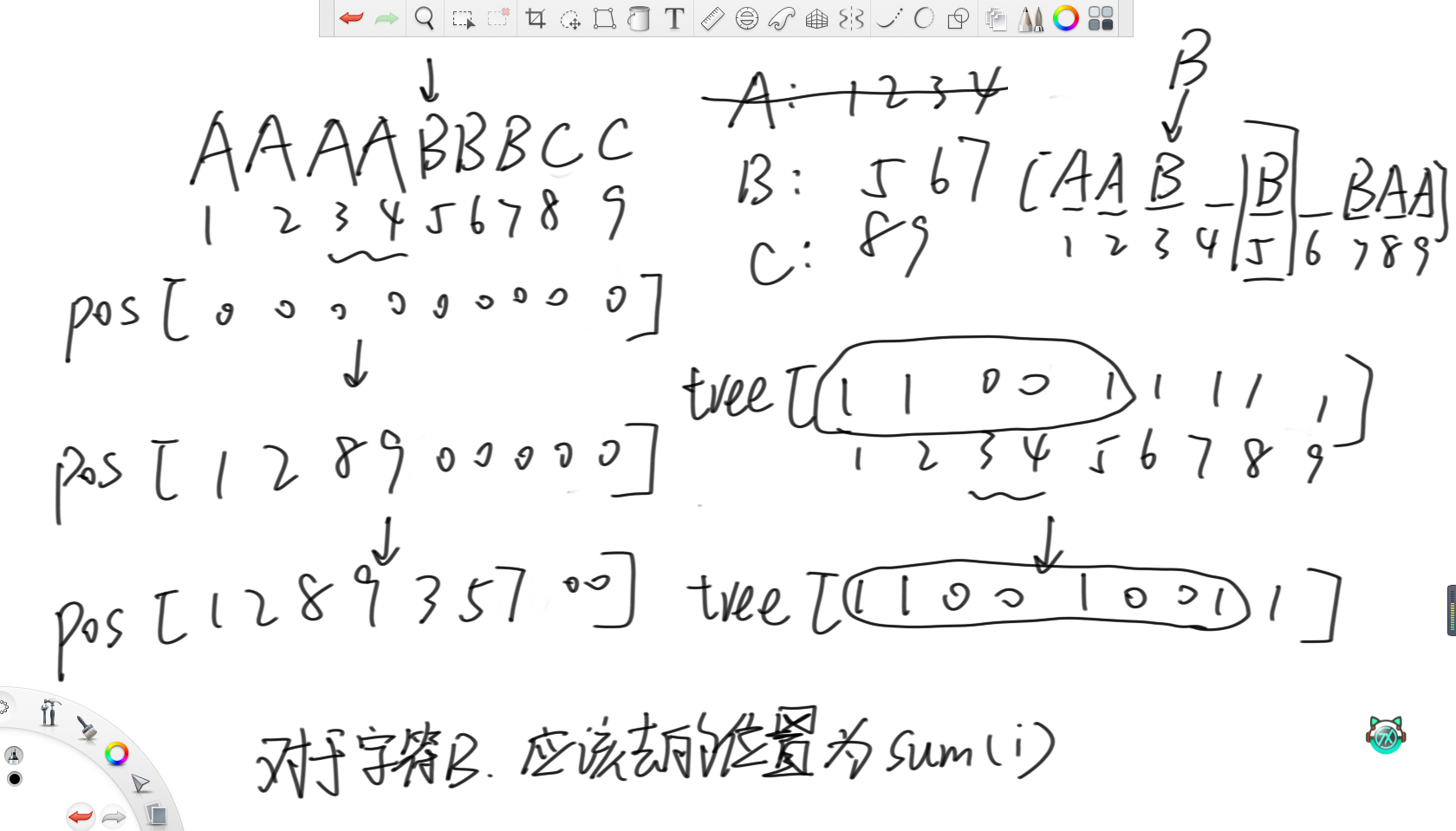
之后，考虑建立pos数组，表示每个位置的字符应该去的位置。之后，用树状数组维护哪个位置的字符被移动走了，初始每个位置都是1。那么对于每个来到的字符，其应该去的位置就是树状数组中1~i的前缀和。由于将一个字符移到了左侧，所以考虑将最右出现的这个字符移到右侧去，然后在树状数组中将这个被移走了的字符的位置改为0。

在上面例子中，当来到第一个A，应该去的位置就是树状数组中1~1上的累加和，那就是1位置。然后最右4位置的A移到9位置，然后把树状数组的4位置从1改成0。第二个A类似。当来到第一个B时，应该去的位置为树状数组1~5的累加和，那就是3位置。然后把7位置的B移到7位置，树状数组的7位置改成0。之后，由于B只剩一个，所以必然要去整个字符串的中点位置。之后C字符以此类推。

当求出pos数组后，观察可得，此时pos数组的次序对数量就是需要移动的次数。在上面例子中，从右往左看，可以写出所有的逆序对。所以移动的方法就是，先处理以9开头的逆序对，那就是将4位置的A移动到9位置。之后，让3位置的A移动到8位置。最后让7位置的B移动回7位置，再让6位置的B移动5位置即可。

虽然这个位置表第一眼看上去很像邻接表，但由于要每次取某个字符最右出现的位置，所以这里用了一种类似链式前向星的方式构建。方法就是设置ends数组和pre数组，ends数组存每个字符最右出现的位置，之后根据pre往前跳就是之前出现的位置。那么要取最右位置只需要从ends里取，然后把ends更新成跳去的pre里的值即可。

总结

感觉最近有点懈怠，刷题听课很容易走神，要赶紧调整回来！

END