传输线的瞬时阻抗
传输线的瞬时阻抗:
下面通过建立一个传输线的简单物理模型,定量分析传输线的瞬时阻抗问题。传输线模型由一排小电容器组成,其值等于传输线的1跨度的电容量,1跨度就是我们(信号)的1步长。我们把这个模型(用于工程感悟的最简易模型)称为传输线的零阶模型。如图7.9所示,这是一个物理模型。它并不是一个等效电路模型,电路模型中不包含物理长度。
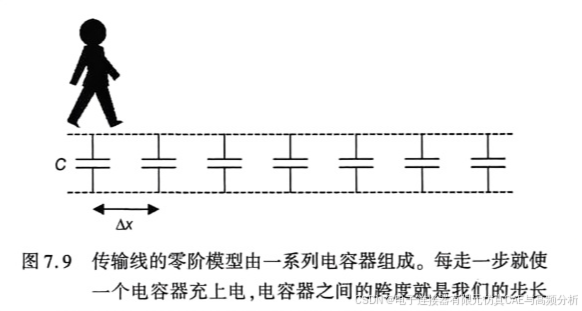
在这个模型中,步长为△x,每个小电容器的大小就是传输线单位长度电容与步长的乘积,即
=
使用这个模型可以计算从脚底流出的电流I。电流的大小就是在每步时间间隔内从我们脚底流出并注入每个电容器的电量。注入电容器的电量Q等于电容乘以其两端的电压V。每走1步,就把电量Q注入导线。
两步之间的时间间隔△t等于步长△x除以信号的速度v。当然,传输实际信号时,步长非常小,但时间间隔也非常小。每个时间间隔内需要的电量,也就是信号在导线上传播时的电流,是一个常量,即
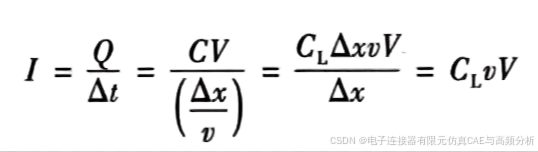
其中,I表示信号的电流,Q表示每一步的电量,C表示每一步的电容,△t表示从一个电容器跨步到另一个电容器的时间,表示传输线单位长度电容,△x表示电容器之间的跨度或步长,v表示信号的速度,V表示信号的电压。
这就是说,从我们脚底流出并注入导线上的电流仅与单位长度电容、信号的传播速度及信号的电压有关,与我们的推论完全吻合。
这就是我们所定义的传输线电流-电压(I-V)特性,它说明了传输线上任何一处的瞬时电流与电压成正比。如果施加的电压加倍,则流入传输线的电流也加倍。这与电阻的特性是完全一致的。所以,在传输线上每前进一步时,信号受到的阻抗就与一个电阻性负载的特性一样。
根据这个关系式可计算出信号沿传输线传播时受到的瞬时阻抗。瞬时阻抗等于施加的电压与流过元器件的电流的比值,即
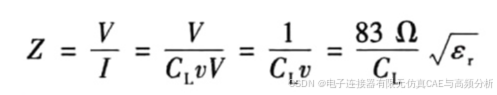
其中,Z表示传输线的瞬时阻抗(单位为Ω),表示单位长度电容量(单位为pF/in),v表示材料中的光速,
![]() 表示材料的介电常数。
表示材料的介电常数。
所以,信号受到的瞬时阻抗仅由传输线的两个固有参数决定,即由传输线的横截面和材料的特性共同决定,与传输线的长度无关。只要这两个参数保持不变,信号受到的瞬时阻抗就是一个常数。当然,与其他阻抗一样,用于度量传输线瞬时阻抗的单位仍是Ω。
由于信号的速度取决于材料特性,所以可得出传输线单位长度电容和瞬时阻抗的关系。例如,若介电常数为4,单位长度电容为3.3 pF/in,则传输线的瞬时阻抗为
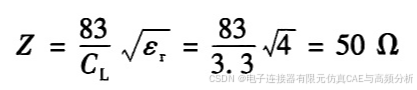
这时我们会问,传输线的电感是多少?它在这个模型中起到什么作用?答案是,这个零阶模型是物理模型而不是电气模型。在这个模型中,我们不是用电感和电容去近似传输线的,而是侧重于信号的速度是材料中的光速。
实际上,制约信号速度的部分原因就是信号路径和返回路径之间的串联回路电感。如果使用的是一阶等效电路模型,其中包含了单位长度电感,就可以导出传输线的电流和有限的传播速度,但是从数学角度讲,模型就变得更加复杂了。
关于传播速度和单位长度电感的关系,这两个模型实际上是等效的。我们将会看到,传播时延与单位长度电容及单位长度电感直接相关。在信号的速度中,已经有对导体电感的某种假设。
