机器学习——08 特征降维
1 特征降维
-
为什么要进行特征降维?特征对于训练模型很关键,但训练数据里可能有不重要的特征,导致模型泛化性能不佳;
-
比如有些特征取值接近,能提供的信息少;
-
又比如如果两个特征变化趋势高度一致,就会存在冗余信息,不能给模型带来新的有用信息;
-
-
特征降维目的:在特定条件下减少特征的数量;
-
因为特征降维涉及多种知识,目前常用的方法有低方差过滤法、PCA(主成分分析)降维法以及相关系数(包括皮尔逊相关系数和斯皮尔曼相关系数)等。
2 低方差过滤法
-
低方差过滤法
-
核心思想是删除方差低于设定阈值的特征;
-
特征方差小意味着特征值波动范围小,能提供的信息少,模型很难从中学习到有用的内容;
-
特征方差大则表示特征值波动范围大,包含的信息相对丰富,更有利于模型学习;
-
-
API
-
sklearn.feature_selection.VarianceThreshold(threshold = 0.0):这是用于实现低方差过滤的类,实例化这个对象可以用来删除所有低方差特征,这里的阈值默认是0.0; -
variance_obj.fit_transform(X):其中X是numpy array格式的数据,形状为[n_samples, n_features],这个方法会对数据进行处理; -
返回值:会删除训练集中方差低于阈值的特征。默认情况下是保留所有非零方差特征,也就是会删除所有样本中具有相同值的特征。
-
-
例:
from sklearn.feature_selection import VarianceThreshold import pandas as pddata = pd.read_csv('data/垃圾邮件分类数据.csv') print(data.shape)# 低方差过滤法 transform =VarianceThreshold(threshold=0.1) x =transform.fit_transform(data) print(x.shape)
3 主成分分析
-
PCA(Principal Component Analysis)的作用是对数据的维数进行压缩;
-
在尽可能降低原数据的维数(也就是复杂度)的同时,只损失少量信息;
-
在这个过程中,可能会舍弃原有数据,并创造新的变量;
-
下图也形象地展示了PCA的过程,将三维数据映射到二维空间,用1st PC和2nd PC来表示新的主成分
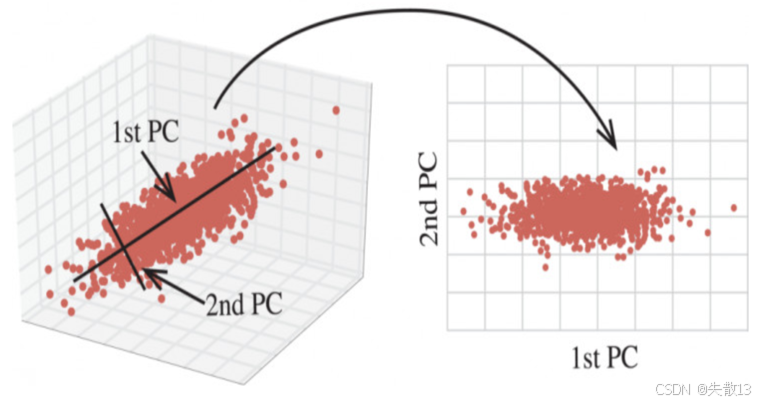
-
-
API
-
sklearn.decomposition.PCA(n_components=None):这个类用于将数据分解到较低维数的空间;- 其中
n_components参数很关键,如果是小数,表示保留百分之多少的信息;如果是整数,表示将特征减少到指定的数量;
- 其中
-
mypcaobj.fit_transform(X):这是对数据进行拟合和转换的方法; -
返回值:是转换后指定维度的数组(array)。
-
-
例:
from sklearn.decomposition import PCA # 从 sklearn 的 datasets 模块中导入 load_iris 函数,用于加载鸢尾花数据集 from sklearn.datasets import load_iris# PCA # 使用 load_iris 函数加载鸢尾花数据集,并通过 return_X_y=True 指定返回特征数据 x 和标签数据 y x,y=load_iris(return_X_y=True) print(x)# 创建一个 PCA 对象,n_components=0.95 表示希望保留 95% 的原始数据方差 pca1=PCA(n_components=0.95) # 对特征数据 x 进行 PCA 降维处理,fit_transform 方法会先拟合数据,然后进行转换 print(pca1.fit_transform(x))# 创建另一个 PCA 对象,n_components=3 表示将特征数据降到 3 维 pca1=PCA(n_components=3) print(pca1.fit_transform(x))
4 PCA相关系数法
-
相关系数基础概念
- 作用:相关系数是反映特征列之间(变量之间)密切相关程度的统计指标;
- 常见类型:常见的有皮尔逊相关系数和斯皮尔曼相关系数;
- 取值范围与性质:相关系数的值介于-1与+1之间,即−1≤r≤+1-1\leq r\leq +1−1≤r≤+1
- 当r>0r>0r>0时,表示两变量正相关;r<0r<0r<0时,两变量为负相关
- 当∣r∣=1|r| = 1∣r∣=1时,表示两变量为完全相关;当r=0r = 0r=0时,表示两变量间无相关关系
- 当0<∣r∣<10<|r|<10<∣r∣<1时,表示两变量存在一定程度的相关,且∣r∣|r|∣r∣越接近1,两变量间线性关系越密切;∣r∣|r|∣r∣越接近于0,表示两变量的线性相关越弱
- 三级划分:一般可按三级划分相关性:∣r∣<0.4|r|<0.4∣r∣<0.4为低度相关;0.4≤∣r∣<0.70.4\leq|r|<0.70.4≤∣r∣<0.7为显著性相关;0.7≤∣r∣<10.7\leq|r|<10.7≤∣r∣<1为高度线性相关
-
皮尔逊相关系数
-
公式:
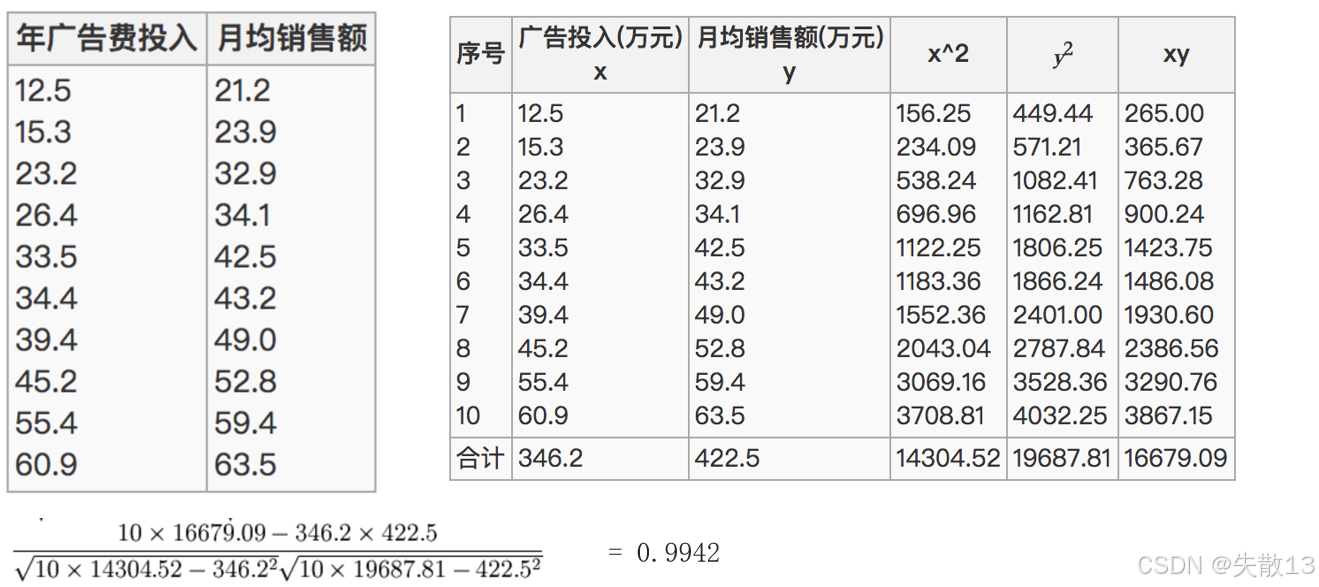
r=n∑xy−∑x∑yn∑x2−(∑x)2n∑y2−(∑y)2 r=\frac{n\sum xy-\sum x\sum y}{\sqrt{n\sum x^{2}-(\sum x)^{2}}\sqrt{n\sum y^{2}-(\sum y)^{2}}} r=n∑x2−(∑x)2n∑y2−(∑y)2n∑xy−∑x∑y -
例子:已知广告投入xxx特征与月均销售额yyy之间的关系,通过给定的数据计算,得出皮尔逊相关系数为0.9942,属于高度相关;
-
-
斯皮尔曼相关系数
-
公式:
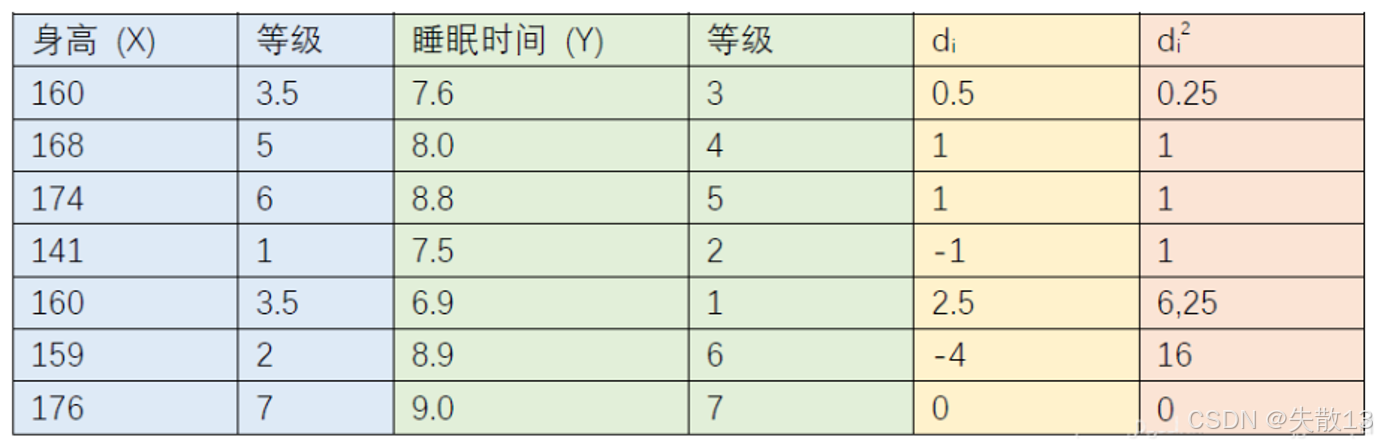
RankIC=1−6∑di2n(n2−1) RankIC = 1-\frac{6\sum d_{i}^{2}}{n(n^{2}-1)} RankIC=1−n(n2−1)6∑di2- 其中nnn为等级个数,ddd为成对变量的等级差数;
-
例子:以身高(X)(X)(X)和睡眠时间(Y)(Y)(Y)为例,通过计算成对变量的等级差数的平方和等,可利用上述公式计算斯皮尔曼相关系数;
-
-
例:
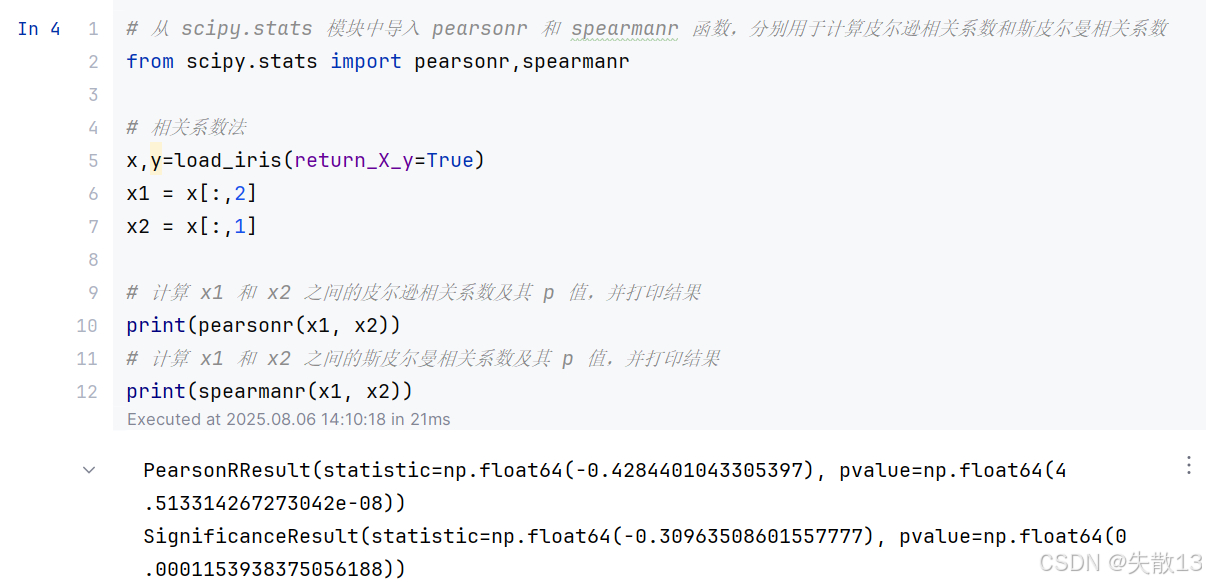
- 皮尔逊相关系数结果:
PearsonRResult(statistic=np.float64(-0.4284401043305397), pvalue=np.float64(4.513314267273042e-08))statistic是皮尔逊相关系数,值为 -0.4284,表明x1和x2之间存在中等程度的负相关pvalue是相关系数的显著性水平,值为 4.5133e-08,远小于 0.05,说明这种负相关关系是显著的
- 斯皮尔曼相关系数结果:
SignificanceResult(statistic=np.float64(-0.30963508601557777), pvalue=np.float64(0.0001153938375056188))statistic是斯皮尔曼相关系数,值为 -0.3096,表明x1和x2之间存在较弱的负相关pvalue是相关系数的显著性水平,值为 0.000115,小于 0.05,说明这种负相关关系也是显著的
- 皮尔逊相关系数结果:
