不同的子序列-二维动态规划

不同的子序列

---

Solution

有点像背包dp

#include<iostream>
#include<vector>
#include<string>
using namespace std;//递归做法
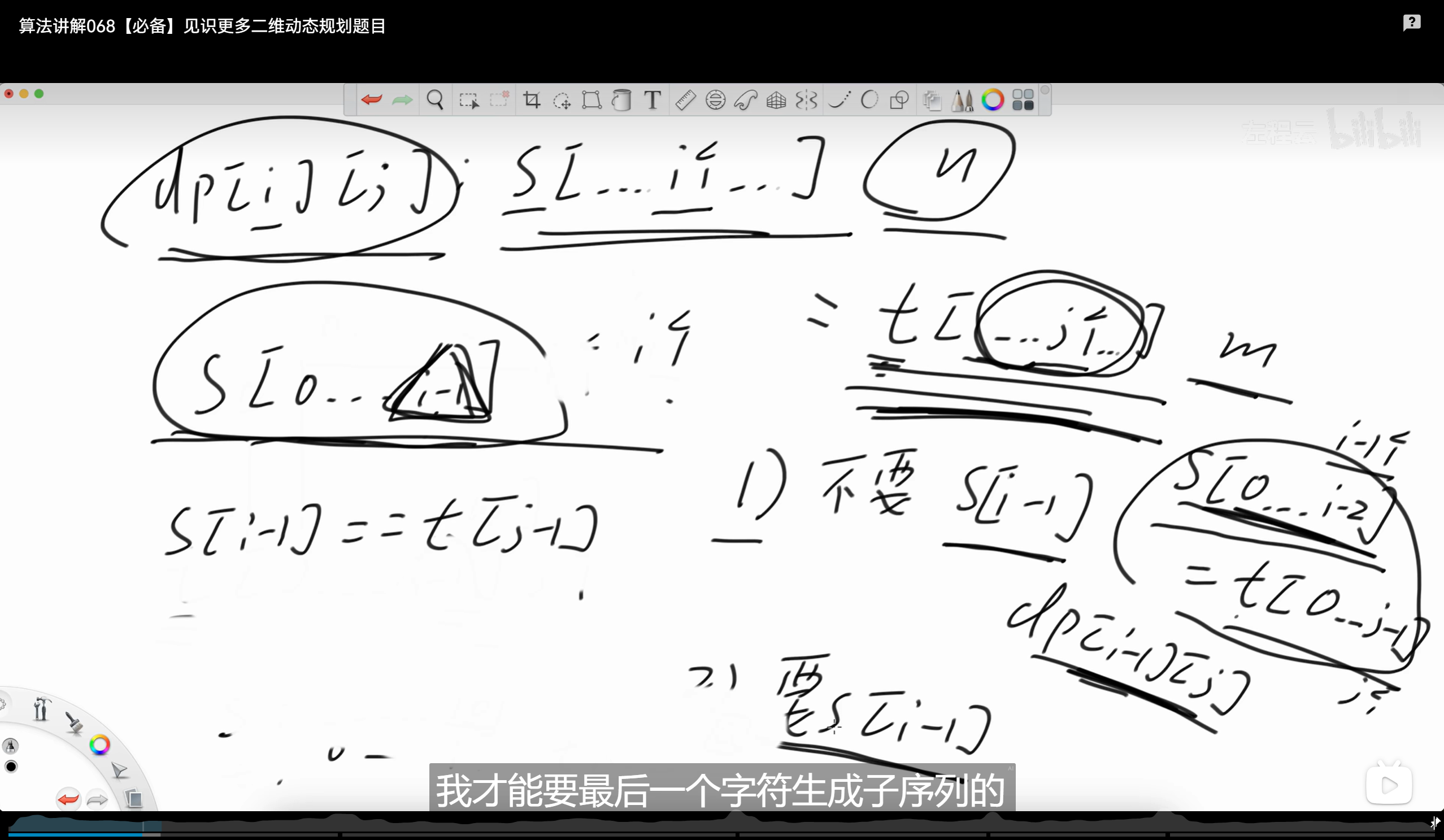
//f(i,j)表示从从字符串s的i开始到结尾，能够选出从字符串t从j到结尾的方案数
//相当于一个背包问题，s是n1件物品，每件物品选择拿和不拿，相等才可以拿，一直到把t所需要的都拿到手才表示一种方案结束
int f1(string s, string t, int i, int j) {int n1 = s.length();int n2 = t.length();if (j == n2) return 1;if (i == n1) return 0;int ans = f1(s, t, i + 1, j);if (s[i] == t[j]) ans += f1(s, t, i + 1, j + 1);return ans;
}//带缓存表的递归
int f2(string s, string t, int i, int j, vector<vector<int>>& dp) {int n1 = s.length();int n2 = t.length();if (j == n2) return 1;if (i == n1) return 0;if (dp[i][j] != -1) return dp[i][j];int ans = f2(s, t, i + 1, j, dp);if (s[i] == t[j]) ans += f2(s, t, i + 1, j + 1, dp);dp[i][j] = ans;return ans;
}//dp做法
unsigned long long f3(string s, string t) {int n1 = s.length();int n2 = t.length();vector<vector<unsigned long long>>dp(n1 + 1, vector<unsigned long long>(n2 + 1, 0));for (int i = n1; i >= 0; --i) {for (int j = 0; j <= n2; ++j) {//注意边界情况，递归的时候怎么写的，dp就怎么写if (j == n2) { dp[i][j] = 1; continue; }if (i == n1) { dp[i][j] = 0; continue; }unsigned long long ans = dp[i + 1][j];if (s[i] == t[j])ans += dp[i + 1][j + 1];dp[i][j] = ans;}}return dp[0][0];
}//dp+空间压缩
unsigned long long f4(string s, string t) {int n1 = s.length();int n2 = t.length();vector<unsigned long long>dp(n2 + 1,0);for (int i = n1; i >= 0; --i) {for (int j = 0; j <= n2; ++j) {if (j == n2) { dp[j] = 1; continue; }if (i == n1) { dp[j] = 0; continue; }unsigned long long ans = dp[j];if (s[i] == t[j]) ans += dp[j + 1];dp[j] = ans;}}return dp[0];
}
int numDistinct1(string s, string t) {return f1(s, t, 0, 0);
}int numDistinct2(string s, string t) {int n1 = s.length();int n2 = t.length();vector<vector<int>>dp(n1 + 1, vector<int>(n2 + 1, -1));return f2(s, t, 0, 0, dp);
}int numDistinct3(string s, string t) {return f3(s, t);
}int numDistinct(string s, string t) {return f4(s, t);
}
int main() {return 0;
}