树和二叉树和算法复杂度
树
节点(Node):
树由一系列的节点组成,每个节点可以包含数据和指向其他节点的链接。
节点通常包含一个数据元素和若干指向其他节点的指针
根节点(Root):
树的顶部节点称为根节点,它是树中没有父节点的唯一节点
子节点(Child):
一个节点的子节点是指由该节点直接指向的节点
叶节点(Leaf):
没有子节点的节点称为叶节点或终端节点
深度(Depth):
节点的深度是从根节点到该节点的路径上的边数。
(广)度:
最大的节点的度
二叉树
n个结点的有限集合,每个节点最多有两个子节点的树,通常称为左子节点和右子节点
特点
1,每个结点最多两个子树。
2,左子树和右子树是有顺序的,次序不能颠倒。
3,如果某个结点只有一个子树,也要区分左,右子树。
特殊的二叉树
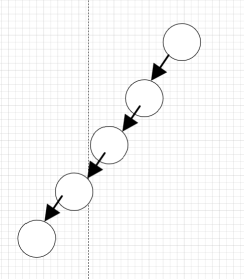
1,斜树,“所有的结点都只有左子树,左斜树,所有结点都只有右子树,右树。
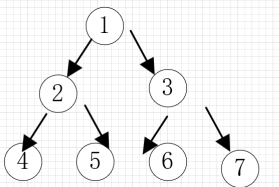
2,满二叉树,所有的分支结点都存在左右子树,并且叶子都在同一层上。
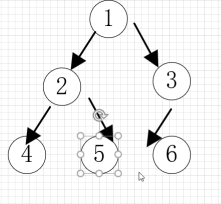
3,完全二叉树,对于一颗有n个结点的二叉树按层序编号,如果编号i(1<=i<=n)的结点于同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这可树为完全二叉树。
特性
1.在二叉树的第i层上最多有2^(i-1)个结点i>=1
2.深度为k的二叉树至多有2^k-1个结点k>=1
3.任意一个二叉树T,如果其叶子结点的个数是n0,度数为2的结点数为n2,n0=n2+1;
4.有n个结点的完全二叉树深度为(logn/log 2)+1;
满二叉树:
在不增加层数的情况下,不能再增加节点了,即为满二叉树
第K层节点个数:
2^(k-1)
K层满二叉树:
总结点数:2^K - 1
完全二叉树:
在满二叉树的基础下,删除节点,只能从右至左,从下到上,删若干个
添加节点,只能从左至右,从上到下,添加若干个。
满二叉树一定是完全二叉树
完全二叉树不一定是满二叉树
二叉树的遍历
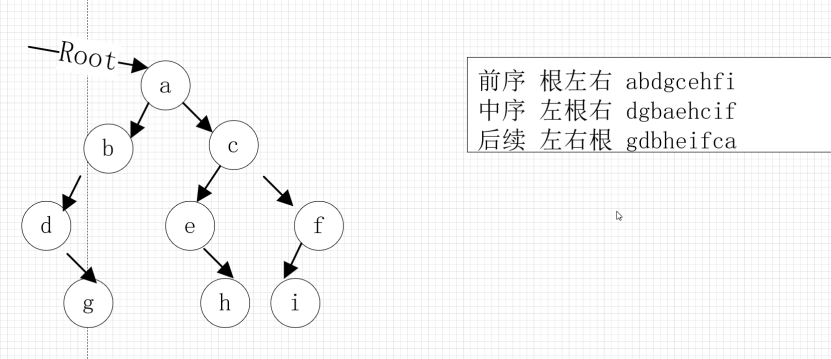
前序遍历:先遍历根,再遍历左子树然后再遍历右子树
中序遍历:先遍历左子树,再遍历根,再遍历右子树
后序遍历:先遍历左子树,再遍历右子树,最后遍历根
层序遍历:从上到下,从左至右,逐层遍历
前三种称为深度优先,层序遍历称为广度优先
已知一种排序,不能还原出唯一的二叉树
已知前序+中序 --->唯一的二叉树
已知后序+中序 --->唯一的二叉树
但是知道前序和后序不能还原

算法
算法即解决特定问题求解步骤
算法的设计
1.正确性
语法正确
合法的输入得到合理的结果
对非法的输入,给出满足要求的规格说明
对精心选择,甚至刁难的测试都能正常运行,结果正确
2.可读性
便于交流,阅读,理解 高内聚,低耦合
3.健壮性
输入非法内容,能进行相应的处理,而不是产生异常
4.高效率(时间复杂度)
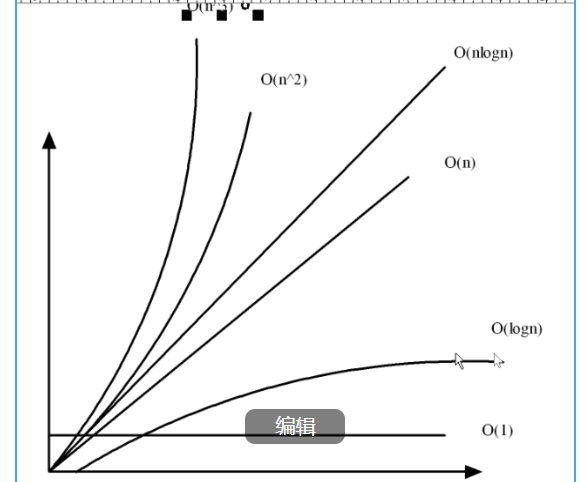
算法时间复杂度:
执行这个算法所花时间的度量
将数据量增长和时间增长用函数表示出来,这个函数就叫做时间复杂度。
一般用大0表示法:0(n)------>时间复杂度是关于数据n的一个函数
随着n的增加,时间复杂度增长较慢的算法时间复杂度低
时间复杂度的计算规则
1,用常数1 取代运行时间中的所有加法常数
2,在修改后的运行函数中,只保留最高阶项
3,如果最高阶存在且系数不是1,则去除这个项相乘的常数
5.低存储(空间复杂度)
空间复杂度越低:低存储 越高:高存储
时间复杂度越低:高效率 越高:低效率