计算机基础速通--数据结构·串的应用

如有问题大概率是我的理解比较片面，欢迎评论区或者私信指正。

友友们，我遇到了一个大问题，技术类的英文面（ai应用开发/java后端偏金融方向）该如何准备？本人英语就过了个六级，脑阔疼额。友友们有啥方法和资料推荐没，可以教教我吗？

考察以基础概念、操作实现(主要是子串的相关操作）、存储结构对比、模式匹配算法（尤其是 KMP）为核心，注重理论理解与代码实现结合，需重点掌握子串相关操作、next数组计算、KMP 优化思想及朴素算法与 KMP 的复杂度对比。

一、基础概念与术语辨析

核心定义考察 可能要求解释串的定义及相关术语

串的定义：由零个或多个字符组成的有限序列。

子串与主串：子串是串中任意连续字符组成的子序列，主串是包含子串的串。

空串与空格串的区别：空串长度为 0，空格串由空格字符组成（每个空格占 1B，如

N=' '。

字符 / 子串的 “位置” 定义：字符位置指其在串中的序号，子串位置指其第一个字符在主串中的位置（位序从 1 开始）。

问题1：“请区分空串和空格串，并举例说明”“子串在主串中的位置如何定义？”

问题2：“Java中，字符串本身可变吗？”Java中，字符串本身是不可变的

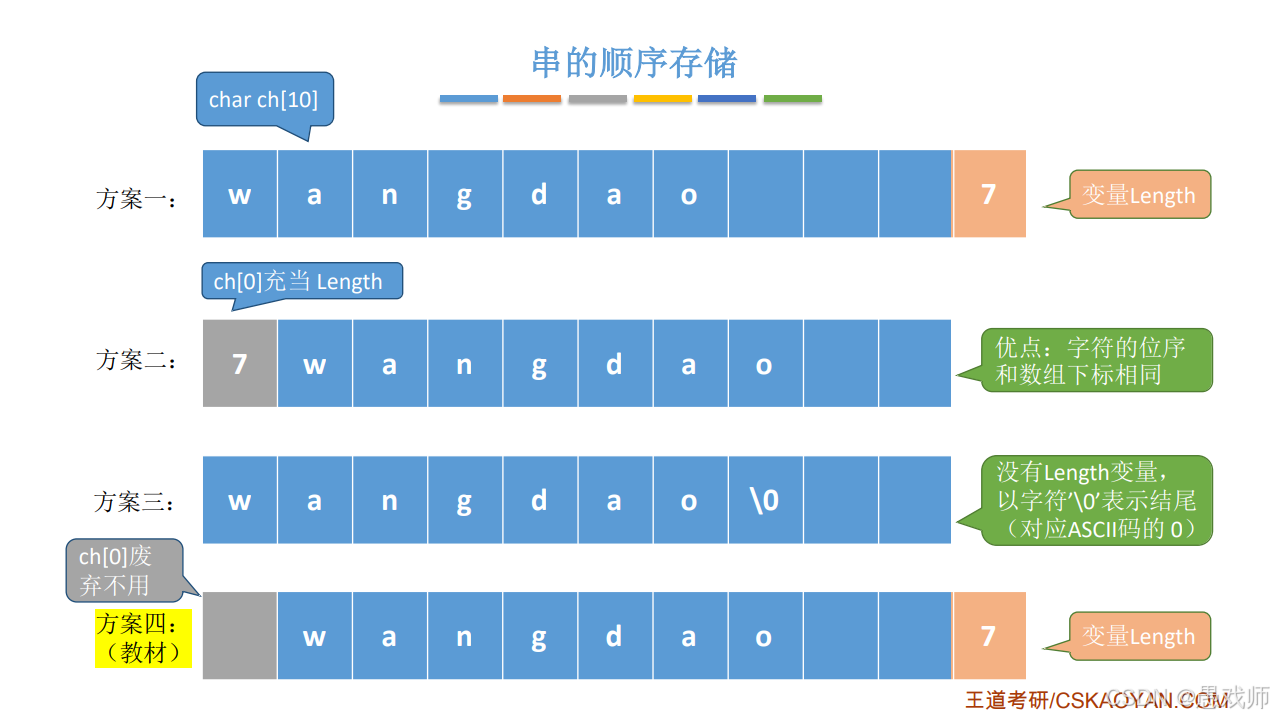
存储结构及优缺点分析

顺序存储

静态数组（定长）：用固定大小数组存储

 优点：随机访问效率高；缺点：长度固定，可能浪费空间或溢出。

动态数组（堆分配）：按实际长度分配空间（）

优点：空间灵活；缺点：需手动管理内存。

public class StringStorageDemo {public static void main(String[] args) {// ============= 静态数组实现串 =============StaticString staticStr = new StaticString(5);staticStr.assign("Hello");System.out.println("静态串内容: " + staticStr);System.out.println("长度: " + staticStr.length());System.out.println("索引2的字符: " + staticStr.charAt(2));// 尝试连接字符串（会截断）staticStr.concat(" World!");System.out.println("连接后(截断): " + staticStr);// ============= 动态数组实现串 =============DynamicString dynamicStr = new DynamicString();dynamicStr.assign("Java");System.out.println("\n动态串初始内容: " + dynamicStr);System.out.println("长度: " + dynamicStr.length());System.out.println("容量: " + dynamicStr.capacity());// 连接字符串（自动扩容）dynamicStr.concat(" is a powerful programming language!");System.out.println("连接后: " + dynamicStr);System.out.println("新长度: " + dynamicStr.length());System.out.println("新容量: " + dynamicStr.capacity());}
}// 静态数组实现的串（定长）
class StaticString {private final char[] data;  // 固定大小数组private int length;         // 实际长度public StaticString(int capacity) {data = new char[capacity];length = 0;}// 赋值操作public void assign(String str) {int copyLength = Math.min(str.length(), data.length);for (int i = 0; i < copyLength; i++) {data[i] = str.charAt(i);}length = copyLength;}// 连接操作（可能截断）public void concat(String str) {int remaining = data.length - length;if (remaining <= 0) return;int copyLength = Math.min(str.length(), remaining);for (int i = 0; i < copyLength; i++) {data[length + i] = str.charAt(i);}length += copyLength;}// 获取字符public char charAt(int index) {if (index < 0 || index >= length) throw new IndexOutOfBoundsException();return data[index];}public int length() {return length;}@Overridepublic String toString() {return new String(data, 0, length);}
}// 动态数组实现的串（堆分配）
class DynamicString {private char[] data;      // 堆分配的数组private int length;       // 实际长度private int capacity;     // 当前容量public DynamicString() {this(16);  // 默认初始容量}public DynamicString(int initialCapacity) {capacity = initialCapacity;data = new char[capacity];length = 0;}// 赋值操作public void assign(String str) {ensureCapacity(str.length());length = str.length();str.getChars(0, length, data, 0);}// 连接操作（自动扩容）public void concat(String str) {ensureCapacity(length + str.length());str.getChars(0, str.length(), data, length);length += str.length();}// 确保容量足够（核心扩容逻辑）private void ensureCapacity(int required) {if (required <= capacity) return;// 计算新容量（通常1.5-2倍增长）int newCapacity = Math.max(required, capacity * 2);char[] newData = new char[newCapacity];// 复制数据System.arraycopy(data, 0, newData, 0, length);// 更新引用和容量data = newData;capacity = newCapacity;System.out.println("扩容至: " + newCapacity);}public char charAt(int index) {if (index < 0 || index >= length) throw new IndexOutOfBoundsException();return data[index];}public int length() {return length;}public int capacity() {return capacity;}@Overridepublic String toString() {return new String(data, 0, length);}
}

实际应用中一般用String-->静态数组的实现，用StringBuilder-->动态数组实现

public class StringStorageDemo {public static void main(String[] args) {// ============= 使用String实现（类似静态数组特性） =============String staticString = "Hello";System.out.println("String实现:");System.out.println("原始内容: " + staticString);System.out.println("长度: " + staticString.length());System.out.println("索引2的字符: " + staticString.charAt(2));// 连接操作 - 创建新对象String newString = staticString.concat(" World!");System.out.println("连接后内容: " + newString);System.out.println("原始对象未变: " + staticString);System.out.println("新对象长度: " + newString.length());// 内存地址比较 - 证明是新对象System.out.println("原始对象地址: " + System.identityHashCode(staticString));System.out.println("新对象地址: " + System.identityHashCode(newString));// ============= 使用StringBuilder实现（类似动态数组特性） =============StringBuilder dynamicString = new StringBuilder("Java");System.out.println("\nStringBuilder实现:");System.out.println("原始内容: " + dynamicString);System.out.println("长度: " + dynamicString.length());System.out.println("容量: " + dynamicString.capacity());System.out.println("索引1的字符: " + dynamicString.charAt(1));// 连接操作 - 原地修改dynamicString.append(" is a powerful programming language!");System.out.println("连接后内容: " + dynamicString);System.out.println("新长度: " + dynamicString.length());System.out.println("新容量: " + dynamicString.capacity());// 内存地址比较 - 证明是同一个对象System.out.println("操作后对象地址: " + System.identityHashCode(dynamicString));// 插入操作展示dynamicString.insert(0, "Awesome ");System.out.println("\n插入后内容: " + dynamicString);System.out.println("最终长度: " + dynamicString.length());System.out.println("最终容量: " + dynamicString.capacity());}
}

链式存储（存储密度）

单字符节点，缺点：存储密度低（1B 字符 + 4B 指针）。

多字符节点：每个节点存多个字符（如 4 个），空闲位置用#补足。 优点：提高存储密度。

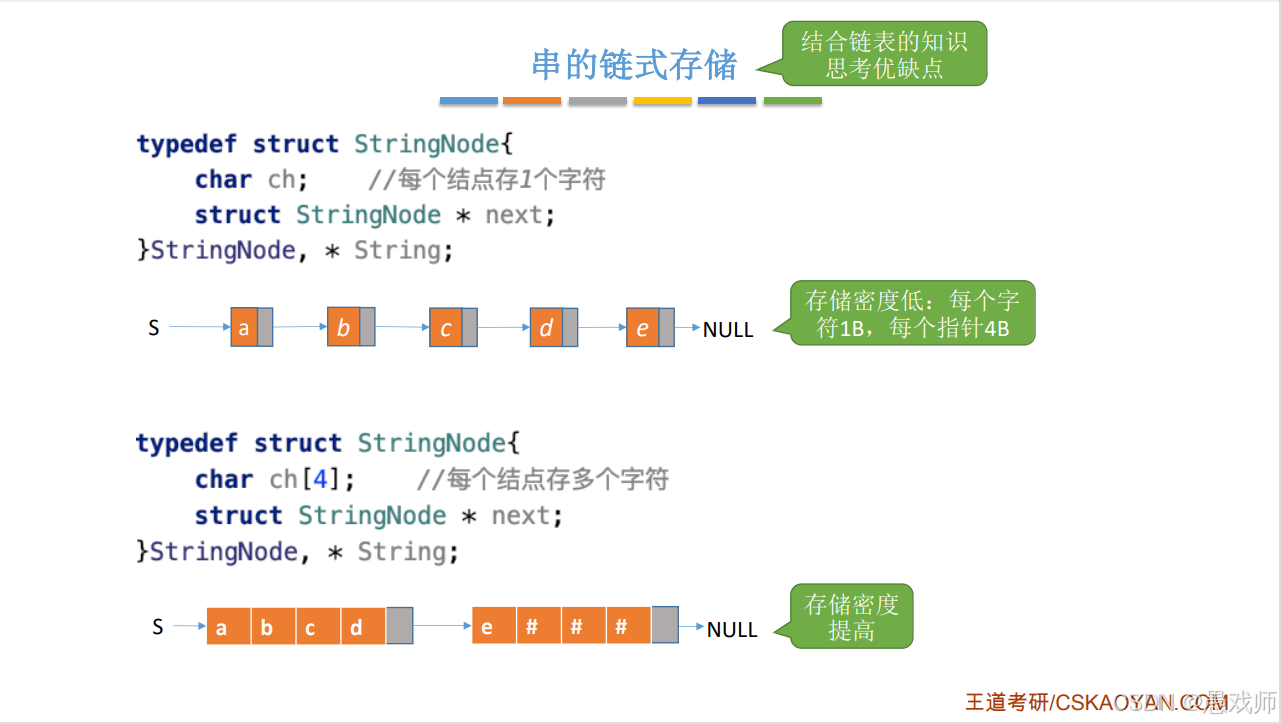
问题1：“串的顺序存储和链式存储各有什么优缺点？针对频繁拼接操作，应选择哪种存储结构？”

优先选择链式存储​​

​​核心优势​​：链式存储在拼接时仅需修改指针，​​避免数据复制​​。

​​优化策略​​：采用​​块链结构​​（如每个结点存4字符），平衡存储密度与操作效率。

单字符节点实现（块状存储）

class CharLinkedList {static class CharNode {char data;CharNode next;CharNode(char c) {this.data = c;}}private CharNode head;private int length;public void append(char c) {CharNode newNode = new CharNode(c);if (head == null) {head = newNode;} else {CharNode current = head;while (current.next != null) {current = current.next;}current.next = newNode;}length++;}public char charAt(int index) {if (index < 0 || index >= length) {throw new IndexOutOfBoundsException();}CharNode current = head;for (int i = 0; i < index; i++) {current = current.next;}return current.data;}// 其他方法：insert, delete, toString 等
}

多字符节点实现（块状存储）

class BlockLinkedList {static class BlockNode {static final int BLOCK_SIZE = 4;char[] data = new char[BLOCK_SIZE];int size = 0; // 当前块中有效字符数BlockNode next;// 添加字符到块中boolean add(char c) {if (size < BLOCK_SIZE) {data[size++] = c;return true;}return false;}// 块中是否已满boolean isFull() {return size == BLOCK_SIZE;}}private BlockNode head;private int totalLength;public void append(char c) {if (head == null) {head = new BlockNode();}BlockNode current = head;BlockNode prev = null;// 查找可以添加字符的块while (current != null && current.isFull()) {prev = current;current = current.next;}if (current == null) {// 所有块已满，创建新块current = new BlockNode();prev.next = current;}current.add(c);totalLength++;}public char charAt(int index) {if (index < 0 || index >= totalLength) {throw new IndexOutOfBoundsException();}BlockNode current = head;int blockIndex = 0;while (current != null) {if (index < blockIndex + current.size) {return current.data[index - blockIndex];}blockIndex += current.size;current = current.next;}throw new IndexOutOfBoundsException();}// 其他方法：insert, delete, toString 等
}

串与线性表的对比

可能通过对比考察对串特殊性的理解：

• 串是特殊的线性表，数据元素间呈线性关系，但数据对象限定为字符集（如中文字符、英文字符等）。

• 串的基本操作（如增删改查）通常以子串为操作对象，而线性表操作多以单个元素为对象。

  典型问题：“串与线性表的主要区别是什么？”

二、基本操作与实现

核心操作功能描述 需掌握串的基本操作定义：

StrAssign（赋值）、StrCopy（复制）、StrEmpty（判空）、StrLength（求长）（至）。

Concat（串联接）：将两个串拼接为新串。

SubString（求子串）：从指定位置提取长度为len的子串。

Index（定位）：返回模式串在主串中首次出现的位置。

StrCompare（比较）：按字符依次对比，返回正值（S>T）、0（S=T）或负值（S<T）。

public class MyString {private char[] value; // 存储字符串的字符数组// 构造函数1：空串public MyString() {this.value = new char[0];}// 构造函数2：通过字符数组创建public MyString(char[] value) {this.value = new char[value.length];System.arraycopy(value, 0, this.value, 0, value.length);}// 构造函数3：通过Java字符串创建public MyString(String str) {this.value = str.toCharArray();}// 1. StrAssign - 赋值操作public void StrAssign(MyString str) {this.value = new char[str.value.length];System.arraycopy(str.value, 0, this.value, 0, str.value.length);}// 2. StrCopy - 复制操作public MyString StrCopy() {return new MyString(this.value);}// 3. StrEmpty - 判空操作public boolean StrEmpty() {return value.length == 0;}// 4. StrLength - 求长度public int StrLength() {return value.length;}// 5. Concat - 串联接public MyString Concat(MyString str) {char[] result = new char[this.value.length + str.value.length];System.arraycopy(this.value, 0, result, 0, this.value.length);System.arraycopy(str.value, 0, result, this.value.length, str.value.length);return new MyString(result);}// 6. SubString - 求子串public MyString SubString(int pos, int len) {if (pos < 0 || pos >= value.length || len < 0 || pos + len > value.length) {throw new IndexOutOfBoundsException("Invalid substring parameters");}char[] sub = new char[len];System.arraycopy(value, pos, sub, 0, len);return new MyString(sub);}// 7. Index - 定位（朴素模式匹配）public int Index(MyString pattern) {if (pattern.StrEmpty()) return 0; // 空模式串总是匹配int n = this.StrLength();int m = pattern.StrLength();for (int i = 0; i <= n - m; i++) {int j;for (j = 0; j < m; j++) {if (value[i + j] != pattern.value[j]) {break;}}if (j == m) return i; // 匹配成功}return -1; // 未找到}// 8. StrCompare - 比较操作public int StrCompare(MyString other) {int len1 = this.StrLength();int len2 = other.StrLength();int minLen = Math.min(len1, len2);for (int i = 0; i < minLen; i++) {if (this.value[i] != other.value[i]) {return this.value[i] - other.value[i];}}// 共同部分相同，比较长度return len1 - len2;}// 辅助方法：转换为Java字符串@Overridepublic String toString() {return new String(value);}// 测试用例public static void main(String[] args) {// 创建字符串MyString s1 = new MyString("Hello");MyString s2 = new MyString("World");MyString s3 = new MyString("HelloWorld");System.out.println("===== 基本操作测试 =====");System.out.println("s1: " + s1 + ", 长度: " + s1.StrLength());System.out.println("s2: " + s2 + ", 长度: " + s2.StrLength());System.out.println("s1是否为空: " + s1.StrEmpty());// 复制操作MyString s1Copy = s1.StrCopy();System.out.println("\n===== 复制操作 =====");System.out.println("s1的副本: " + s1Copy);// 串联接操作MyString concatResult = s1.Concat(s2);System.out.println("\n===== 串联接操作 =====");System.out.println(s1 + " + " + s2 + " = " + concatResult);// 求子串操作System.out.println("\n===== 求子串操作 =====");MyString sub = s3.SubString(3, 5);System.out.println(s3 + " 的子串(从位置3开始长度5): " + sub);// 定位操作System.out.println("\n===== 定位操作 =====");MyString pattern = new MyString("loW");int index = s3.Index(pattern);System.out.println("在 " + s3 + " 中查找 " + pattern + " 的位置: " + index);// 比较操作System.out.println("\n===== 比较操作 =====");MyString s4 = new MyString("Apple");MyString s5 = new MyString("Banana");System.out.println(s1 + " 与 " + s1Copy + " 比较: " + s1.StrCompare(s1Copy));System.out.println(s1 + " 与 " + s2 + " 比较: " + s1.StrCompare(s2));System.out.println(s4 + " 与 " + s5 + " 比较: " + s4.StrCompare(s5));System.out.println(s5 + " 与 " + s4 + " 比较: " + s5.StrCompare(s4));}
}

题目一字符串反转

344. 反转字符串
考察点：字符串的遍历与元素交换，基础操作实现。

class Solution {public void reverseString(char[] s) {int head=0,tail=s.length-1;while(head<=tail){char temp=s[head];s[head]=s[tail];s[tail]=temp;head++;tail--;}}
}

题目二字符串拼接与分割

151. 反转字符串中的单词
考察点：字符串的分割（按空格）、反转后拼接，处理首尾空格等边界情况。

import java.util.*;class Solution {public String reverseWords(String s) {// 去除字符串首尾空格String trimmed = s.trim();// 如果去除空格后为空，直接返回空字符串if (trimmed.isEmpty()) {return "";}// 按一个或多个空格分割字符串String[] words = trimmed.split("\\s+");// 将数组转换为列表并反转List<String> wordList = Arrays.asList(words);Collections.reverse(wordList);// 用单个空格连接反转后的单词列表return String.join(" ", wordList);}
}

三、模式匹配算法（重点）

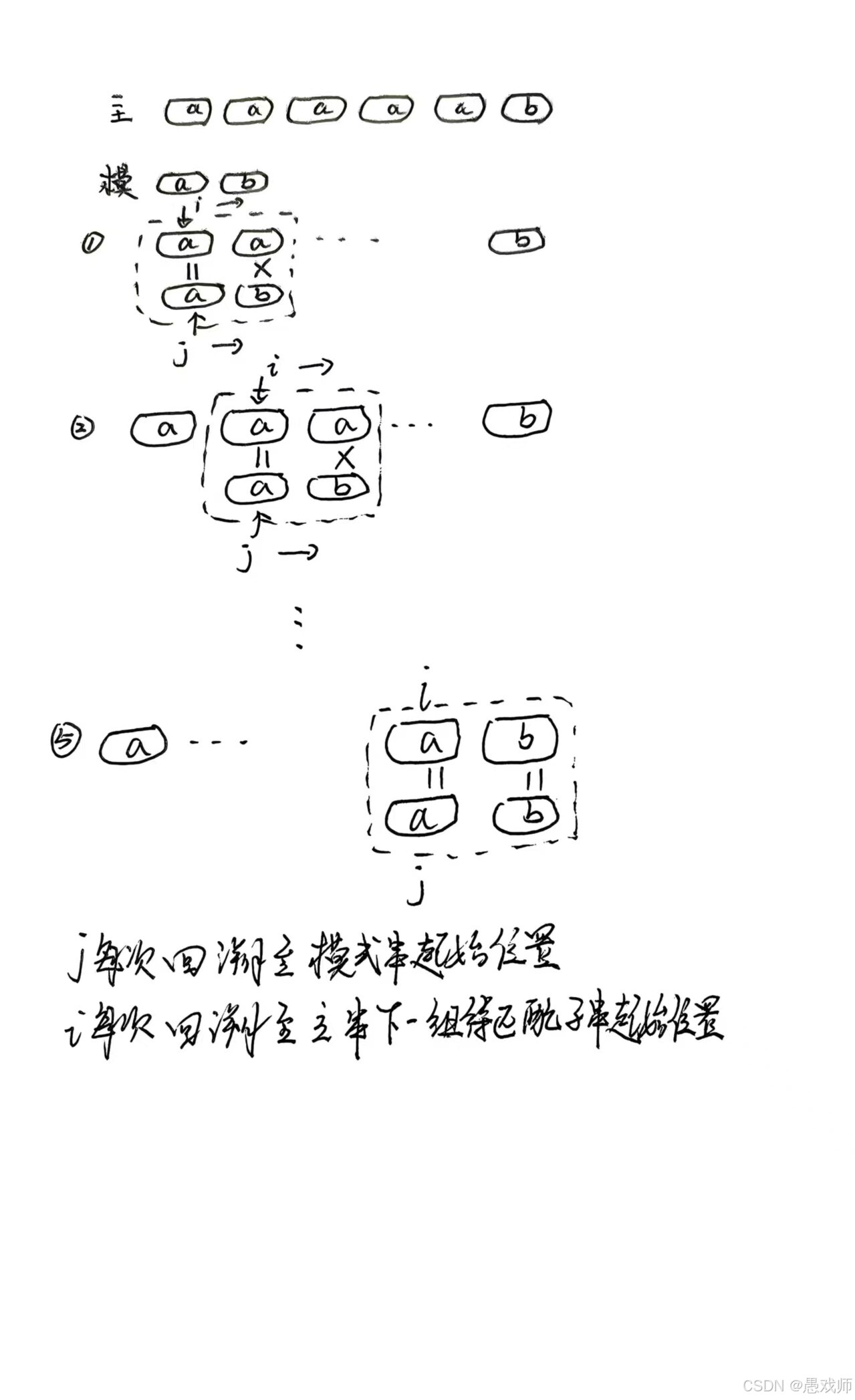
朴素模式匹配算法

思想：将主串中所有长度为模式串长度的子串依次与模式串对比。

时间复杂度：最坏情况（n为主串长度，m为模式串长度），如主串为aaaaab、模式串为ab时。

考察点：手动模拟匹配过程，分析最坏情况成因。

KMP 算法

核心目标： 更快地在主串（文本）S 中找到模式串（关键词）T 出现的位置。

1. 朴素匹配算法的痛点：低效的回溯

想象一下，你想在一本很厚的书（S）里找一个特定的单词（T），比如 "abaabc"。

• 朴素方法： 你从书的第一页第一行第一个字母开始，一个字母一个字母地对比 "abaabc"。

  • 如果第一个字母就不同（比如书上是 b，单词是 a），你立刻把书往后翻一点点（移动一格），重新从单词开头对比。

  • 如果前面几个字母都相同，但到第 5 个字母不同了（比如书上第 5 个是 x，单词第 5 个是 b），你会把书往后翻一点点（移动一格），然后完全从头开始对比单词 "abaabc"，即使你知道刚刚书上的 "abaa" 和单词开头的 "abaa" 是匹配的！这就是低效的来源——主串指针 i 经常回溯。

2. KMP 的聪明想法：利用已知信息，避免回溯主串

KMP 算法观察到一个关键点：当匹配失败时（比如在 T[j] 处失败了），模式串 T[1..j-1] 这一段是和主串 S[i-j+1..i-1] 完全匹配的！ 这个信息非常宝贵，因为这段信息将对未知主串的处理映射转化成对已知的模式串的处理上来，从而有效避免主串指针回溯问题。

KMP 的核心问题是：既然 T[1..j-1] 已经匹配成功了，那么当 T[j] 匹配失败时，我们能不能直接把模式串 T “滑动”到一个新的位置，让这个新位置之前的某个前缀，刚好对上主串 S 中刚匹配成功的那段后缀？并且保持主串指针 i 不动（不回溯）！

• 目标： 找到一个新的位置 k（k < j），使得 T[1..k] = T[j-k..j-1]。

  • T[1..k] 是模式串开头的前 k 个字符（前缀）。

  • T[j-k..j-1] 是模式串匹配失败位置 j 前面 k 个字符（后缀）。

  • 要求这两段相等。

• 为什么这样滑动有效？

  1. 因为主串 S[i-j+1..i-1] = T[1..j-1]（已匹配）。

  2. 滑动后，我们希望 T[1..k] 去对齐 S 中 [i-k..i-1] 这段。

  3. 根据要求 T[1..k] = T[j-k..j-1]，而 T[j-k..j-1] 又等于 S[i-k..i-1]（因为 T[1..j-1] = S[i-j+1..i-1]，取最后 k 个）。

  4. 所以 T[1..k] = S[i-k..i-1]，滑动后，T[1..k] 这段不用重新比较就已经知道匹配了！我们可以直接从 T[k+1] 和 S[i] 开始继续比较（主串 i 没动，模式串指针 j 更新为 k+1）。

3. next 数组：存储“滑动位置”信息

• 定义： next[j] 表示当模式串 T 的第 j 个字符 T[j] 与主串失配时，模式串指针 j 应该回退到的位置（k）加 1。或者说，next[j] 指示了下一次应该用 T 的第 next[j] 个字符去和主串当前失配字符 S[i] 进行比较。

  • 更直观的公式：j 回退到 next[j] (j = next[j])

• 核心任务： next[j] 的值等于 T[1..j-1] 这个子串的最长相等真前缀和真后缀的长度 + 1。

  • 真前缀： 去掉最后一个字符的前缀（如 "aba" 的真前缀有 "a", "ab"）。

  • 真后缀： 去掉第一个字符的后缀（如 "aba" 的真后缀有 "ba", "a"）。

  • 最长相等真前后缀： 找一个最长的字符串，它既是 T[1..j-1] 的真前缀，又是 T[1..j-1] 的真后缀。

  • next[j] = 这个最长长度 + 1

• 为什么是“最长”？ 为了保证滑动的幅度尽可能大（跳过尽可能多的无效比较），同时不会漏掉可能的匹配起点。

• 约定：

  • next[1] = 0：如果模式串第一个字符就失配，主串指针 i 后移一位 (i++)，模式串指针 j 保持为 1 (或者 j 回退到 0 后紧接着 j++ 回到 1，效果一样) 去匹配下一个子串。这对应朴素匹配中“移动一格从头开始”。

  • next[2] = 1：如果模式串第二个字符失配，说明第一个字符是匹配的。此时 T[1..1] 的真前缀和真后缀都是空集（长度 0），next[2] = 0 + 1 = 1。意思是 j 回退到 1，用 T[1] 去和当前 S[i] 比较（虽然 T[1] 之前匹配过，但主串 i 没动，当前 S[i] 是导致 T[2] 失配的那个字符，所以需要重新比较 T[1] 和它是否匹配）。

4. 手算 next 数组（核心：找最长相等真前后缀）

以模式串 T = "abaabc" 为例：

j	T[1..j]	T[1..j-1]	T[1..j-1] 的最长相等真前后缀长度 L	next[j] = L + 1	解释
1	a	-	- (约定)	0	第一个字符失配，i++, j 重置
2	ab	a	真前缀：[] 真后缀：[] L = 0	1	第二个字符失配，回退到第一个字符 T[1] 比较
3	aba	ab	真前缀：["a"] 真后缀：["b"] 不相等 L = 0	1	第三个字符失配，回退到第一个字符 T[1] 比较
4	abaa	aba	真前缀：["a", "ab"] 真后缀：["ba", "a"] 相等部分："a" (长度1) L = 1	2	第四个字符失配，回退到第二个字符 T[2] 比较
5	abaab	abaa	真前缀：["a", "ab", "aba"] 真后缀：["baa", "aa", "a"] 相等部分："a" (长度1) L = 1	2	第五个字符失配，回退到第二个字符 T[2] 比较
6	abaabc	abaab	真前缀：["a", "ab", "aba", "abaa"] 真后缀：["baab", "aab", "ab", "b"] 相等部分："ab" (长度2) L = 2	3	第六个字符失配，回退到第三个字符 T[3] 比较

最终 next 数组：next[] = [0, 1, 1, 2, 2, 3] (通常 next[0] 不用，下标从 1 开始对应 j)

5.代码实现（Java中一般用0-base)

public class KMPMatcher {// 构建next数组（部分匹配表）public static int[] getNextArray(char[] ms) {if (ms.length == 1) {return new int[]{-1};}int[] next = new int[ms.length];next[0] = -1;next[1] = 0;int i = 2;  // next数组填充位置int cn = 0; // 当前比较位置while (i < ms.length) {if (ms[i - 1] == ms[cn]) {//next[i]=cn+1;//cn++;//i++;next[i++] = ++cn;} else if (cn > 0) {cn = next[cn];} else {next[i++] = 0;}}return next;}// KMP字符串匹配算法public static int getIndexOf(String s, String m) {// 参数合法性校验if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {return -1;}char[] str1 = s.toCharArray();char[] str2 = m.toCharArray();int i1 = 0; // 主串指针int i2 = 0; // 模式串指针int[] next = getNextArray(str2); // 获取部分匹配表while (i1 < str1.length && i2 < str2.length) {if (str1[i1] == str2[i2]) {i1++;i2++;  // 字符匹配成功，双指针后移} else if (next[i2] == -1) {i1++;  // 模式串首位不匹配，主串后移} else {i2 = next[i2];  // 利用next数组跳过已匹配前缀}}// 返回匹配起始位置或-1return i2 == str2.length ? i1 - i2 : -1;}// 使用示例public static void main(String[] args) {String text = "ababaabaabc";String pattern = "abaabc";int index = getIndexOf(text, pattern);System.out.println("匹配位置: " + index);  // 输出: 5}
}

求next数组的的关键在于cn，(1、cn指的是p[1..i-1]的最长前后缀长度；2、cn指的是与i-1元素进行比较的元素的下标位置），next[0]=-1作为回退边界

kmp的关键在于next数组的回退过程，回退边界判断和返回值。我的理解可能比较片面，可以参考以下大佬的讲解，建议从1：28：00开始看。

基础提升：2 有序表、并查集等_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Ef4y1T7Qi?spm_id_from=333.788.player.switch&vd_source=4b89f462036a892baf8931104a1f36b1&p=35

• next 数组的意义： 它告诉我们在模式串 T 的 j 位置匹配失败时，应该把 j 回退到哪个位置（next[j]）去继续和主串当前的 S[i] 比较。主串指针 i 永不回溯！

• next[j] 的计算本质： 就是求 T[1..j-1] 这个子串的最长相等真前缀和真后缀的长度 + 1。这个值完全由模式串 T 自身决定。

• 效率提升： 通过 next 数组，KMP 避免了主串指针 i 的无效回溯（这是朴素算法慢的主要原因），在失配时能跳过一大段肯定不匹配的位置。预处理 next 数组的时间是 O(m)，匹配过程是 O(n)，整体 O(m+n)，远优于朴素算法的 O(m*n)（尤其在主串和模式串有很多部分匹配时）。

简单来说： KMP 利用匹配失败时已经匹配成功的那部分模式串的信息（体现在 next 数组中），聪明地“滑动”模式串，跳过一些肯定不匹配的位置，让匹配过程加速。next 数组就是这个聪明滑动的导航图。

进一步优化：

nextval数组，解决next数组的冗余跳转（如模式串aaaab的nextval为[0,0,0,0,4]），本质就是利用当前匹配信息，如当前模式串与文本串的当前字符不匹配则文本串的当前字符一定和跳转后相同的模式串字符（如有）不匹配，所以可以在next的基础上写出nextval数组。 

nextval[0] = -1;
nextval[1] = 0;
for (int j = 2; j <= T.length; j++) {if (T.ch[next[j]] == T.ch[j])nextval[j] = nextval[next[j]];elsenextval[j] = next[j];
}

问题1：“KMP 算法相比朴素算法有什么优化？next数组的含义是什么？”

问题2：字符匹配

28. 找出字符串中第一个匹配项的下标 - 力扣（LeetCode）https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/description/

class Solution {public int strStr(String haystack, String needle) {return getIndexOf(haystack,needle);}// 构建next数组（部分匹配表）public static int[] getNextArray(char[] ms) {if (ms.length == 1) {return new int[]{-1};}int[] next = new int[ms.length];next[0] = -1;next[1] = 0;int i = 2;  // next数组填充位置int cn = 0; // 当前比较位置while (i < ms.length) {if (ms[i - 1] == ms[cn]) {//next[i]=cn+1;//cn++;//i++;next[i++] = ++cn;} else if (cn > 0) {cn = next[cn];} else {next[i++] = 0;}}return next;}// KMP字符串匹配算法public static int getIndexOf(String s, String m) {// 参数合法性校验if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {return -1;}char[] str1 = s.toCharArray();char[] str2 = m.toCharArray();int i1 = 0; // 主串指针int i2 = 0; // 模式串指针int[] next = getNextArray(str2); // 获取部分匹配表while (i1 < str1.length && i2 < str2.length) {if (str1[i1] == str2[i2]) {i1++;i2++;  // 字符匹配成功，双指针后移} else if (next[i2] == -1) {i1++;  // 模式串首位不匹配，主串后移} else {i2 = next[i2];  // 利用next数组跳过已匹配前缀}}// 返回匹配起始位置或-1return i2 == str2.length ? i1 - i2 : -1;}}

问题3：“请计算模式串ababaa的next数组和nextval数组”。

class Solution {public int strStr(String haystack, String needle) {return getIndexOf(haystack, needle);}// 构建next数组public static int[] getNextArray(char[] ms) {if (ms.length == 1) {return new int[]{-1};}int[] next = new int[ms.length];next[0] = -1;next[1] = 0;int i = 2;int cn = 0;while (i < ms.length) {if (ms[i - 1] == ms[cn]) {next[i++] = ++cn;} else if (cn > 0) {cn = next[cn];} else {next[i++] = 0;}}return next;}public static int[] getNextvalArray(char[] ms, int[] next) {if (ms.length == 1) {return new int[]{-1};}int[] nextval = new int[ms.length];nextval[0] = -1;  // 固定值for (int i = 1; i < ms.length; i++) {//保证next[i]有效才优化if (next[i] > 0 && ms[i] == ms[next[i]]){nextval[i] = nextval[next[i]];  } else {nextval[i] = next[i];          }}return nextval;}// KMP匹配算法public static int getIndexOf(String s, String m) {if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {return -1;}char[] str1 = s.toCharArray();char[] str2 = m.toCharArray();int i1 = 0;int i2 = 0;int[] next = getNextArray(str2);next = getNextvalArray(str2, next); while (i1 < str1.length && i2 < str2.length) {if (str1[i1] == str2[i2]) {i1++;i2++;} else if (next[i2] == -1) {i1++;} else {i2 = next[i2];}}return i2 == str2.length ? i1 - i2 : -1;}
}

四、算法综合设计与实现

滑动窗口与串结合

3. 无重复字符的最长子串 - 力扣（LeetCode）https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/?envType=study-plan-v2&envId=top-100-liked

滑动窗口 + 哈希集合

​​核心思想​​：

使用左右指针（left和 right）表示当前子串的窗口，并用哈希集合存储窗口内的字符。右指针不断向右扩展，遇到重复字符时，左指针向右移动直至移除重复字符，同时更新最大子串长度。

​​算法步骤​​：

1. ​​初始化​​：

   • 左右指针 left = right = 0

   • 哈希集合 char_set存储窗口字符

   • 最大长度 max_len = 0

2. ​​滑动窗口​​：

   • ​​扩展右指针​​：若 s[right]不在集合中，将其加入集合并更新最大长度。

   • ​​收缩左指针​​：若 s[right]已在集合中，移除 s[left]并将左指针右移，直到重复字符被移除。

3. ​​终止条件​​：右指针到达字符串末尾。

​​时间复杂度​​：O(N)（每个字符最多被遍历两次）

​​空间复杂度​​：O(∣Σ∣)（字符集大小，如 ASCII 为 128）

import java.util.HashSet;
import java.util.Set;class Solution {public int lengthOfLongestSubstring(String s) {// 使用哈希集合存储当前窗口中的字符Set<Character> set = new HashSet<>();int maxLen = 0;    // 最大子串长度int left = 0;       // 滑动窗口左指针// 右指针遍历字符串for (int right = 0; right < s.length(); right++) {char current = s.charAt(right);// 当字符已存在集合中时，移动左指针直到移除重复字符while (set.contains(current)) {set.remove(s.charAt(left));left++;}// 添加当前字符到集合，并更新最大长度set.add(current);maxLen = Math.max(maxLen, right - left + 1);}return maxLen;}
}

438. 找到字符串中所有字母异位词 - 力扣（LeetCode）https://leetcode.cn/problems/find-all-anagrams-in-a-string/description/?envType=study-plan-v2&envId=top-100-liked

​​核心思路​​

• 使用长度为 26 的数组统计字符频次

• 在 s上滑动长度为 p_len的窗口

• 比较窗口频次与 p的频次是否完全一致

​​算法步骤​​

1. 若 len(s) < len(p): 返回空列表

2. 初始化两个数组 s_count 和 p_count（长度26）

3. 遍历前 p_len 个字符，填充两个数组

4. 检查第一个窗口：若两数组相同，记录索引0

5. 滑动窗口： - 移除窗口左端字符（s_count索引减1） - 加入窗口右端新字符（s_count索引加1） - 检查并记录新窗口是否匹配

​​复杂度分析​​

⏱️ 时间复杂度：O(26*(n-m))

n-m次窗口滑动 × 26 次数组比较

💾 空间复杂度：O(1)（固定长度26的数组）

import java.util.ArrayList;
import java.util.List;class Solution {public List<Integer> findAnagrams(String s, String p) {List<Integer> result = new ArrayList<>();int sLen = s.length(), pLen = p.length();if (sLen < pLen) return result;// 创建两个计数数组int[] sCount = new int[26];int[] pCount = new int[26];// 初始化第一个窗口和p的计数for (int i = 0; i < pLen; i++) {pCount[p.charAt(i) - 'a']++;sCount[s.charAt(i) - 'a']++;}// 检查第一个窗口if (arraysEqual(sCount, pCount)) {result.add(0);}// 滑动窗口for (int i = 0; i < sLen - pLen; i++) {// 移除窗口左侧字符sCount[s.charAt(i) - 'a']--;// 添加窗口右侧新字符sCount[s.charAt(i + pLen) - 'a']++;// 检查当前窗口if (arraysEqual(sCount, pCount)) {result.add(i + 1);}}return result;}// 辅助方法：比较两个数组是否相等private boolean arraysEqual(int[] a, int[] b) {for (int i = 0; i < 26; i++) {if (a[i] != b[i]) return false;}return true;}
}

前缀和与串

560. 和为 K 的子数组 - 力扣（LeetCode）https://leetcode.cn/problems/subarray-sum-equals-k/description/?envType=study-plan-v2&envId=top-100-liked

问题定义​​

统计数组中​​和为 k 的连续子数组的个数​​。

​​核心思想​​

1. ​​前缀和转换​​

   • 定义 pre[i]= 数组前 i项和（nums[0]到 nums[i]）

   • 子数组 [j, i]的和转化为：

     ​​pre[i] - pre[j-1] = k​​

     ⇒ ​​pre[j-1] = pre[i] - k  这一步很关键，因为把寻找求和为k的子数组转化为查询是否存在pre[j-1]，即pre[i] - k，问题转化为：​​找有多少个 j满足 pre[j] = pre[i] - k​​，其中 j < i​

2. ​​哈希表优化​​

   • 建立哈希表 map<前缀和, 出现次数>

   • 遍历时动态记录所有前缀和的出现次数

   • 对于每个 pre[i]，查找 ​​pre[i] - k​​ 在历史中出现的次数

在这我用个比喻解释前缀和转化和哈希表优化

想象你在一家商店连续几天记账：

• 每次记账，你记录的是​​从开店至今的总营业额​​

• 你想知道​​连续几天的营业额加起来正好是K元​​的日子有多少次

1. 前缀和是什么？

• 就像记账本里的​​累计营业额​​

• 示例：每日收入 [1元, 2元, 3元]

  • 第一天结束：累计1元

  • 第二天结束：累计3元 (1+2)

  • 第三天结束：累计6元 (1+2+3)

2. 如何找连续几天和为K？

• 假设你想找和为2的连续收入

• 如果你发现：

  • 第三天结束时累计6元

  • 第一天结束时累计4元

• 那么第二天到第三天：6 - 4 = 2元！

这就是核心思想：​​累计营业额差等于K时，中间时段的营业额和就是K​​

3. 如何用哈希表优化？

1. 我们拿个本子记录所有出现过的累计营业额

   • 记录形式：{累计营业额: 出现次数}

   • 初始：记下开店前0元（出现1次）

2. 边记账边检查：

   • 当前累计营业额 = 之前累计 + 今天收入

   • 看看本子上是否记过：[当前累计 - K]的数值？

   • 如果记过，说明这中间有段时间收入正好是K元！

class Solution {public int subarraySum(int[] nums, int k) {if(nums.length<1)return 0;HashMap<Integer,Integer> m=new HashMap<>();m.put(0,1);int count=0,pre_sum=0;for(int i=0;i<nums.length;i++){pre_sum+=nums[i];int target=pre_sum-k;if(m.containsKey(target)){count+=m.get(target);}m.put(pre_sum,m.getOrDefault(pre_sum,0)+1);}return count;}
}

用前缀和快速计算区间和，用哈希表记住历史值，把两重循环优化成一重遍历。

数组、队列、滑动窗口与串*

239. 滑动窗口最大值 - 力扣（LeetCode）https://leetcode.cn/problems/sliding-window-maximum/?envType=study-plan-v2&envId=top-100-liked

关键思路

1. 用一个双端队列维护当前窗口内 ​​可能成为最大值的元素下标​​。队列中的元素保持从大到小的顺序（单调递减），队首始终是当前窗口的最大值。

   操作步骤

   • ​​初始化​​：处理第一个窗口（前k个元素）

   • ​​维护队列​​（两个关键操作）：

     • ​​队尾维护​​：当新元素≥队尾元素时，弹出队尾（因为旧的较小值不再可能成为最大值）

     • ​​队首维护​​：当队首元素超出窗口范围时，弹出队首

   • ​​记录结果​​：每次窗口移动后，队首就是当前窗口的最大值

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {if(nums.length<1)return new int[]{0};int nlen=nums.length;Deque<Integer> deque=new LinkedList<>();int[] ans=new int[nlen-k+1];//初始化队列for(int i=0;i<k;i++){while(!deque.isEmpty() &&nums[i]>=nums[deque.peekLast()]){deque.pollLast();}deque.offerLast(i);}ans[0]=nums[deque.peekFirst()];//移动队列for(int i=k;i<nlen;i++){//向右移动,维持单调while(!deque.isEmpty() &&nums[i]>=nums[deque.peekLast()]){deque.pollLast();}deque.offerLast(i);//判断队首是否在窗口内while(!deque.isEmpty() && deque.peekFirst()<=i-k){deque.pollFirst();}ans[i-k+1]=nums[deque.peekFirst()];}return ans;}
}

动态规划与串*

题目：回文判断（动态规划、中心扩展）

5. 最长回文子串 - 力扣（LeetCode）https://leetcode.cn/problems/longest-palindromic-substring/description/

class Solution {public String longestPalindrome(String s) {if (s == null || s.length() < 1) return "";int start = 0, end = 0; // 记录最长回文的起止位置for (int i = 0; i < s.length(); i++) {// 奇数长度扩展 (中心点为i)int len1 = expand(s, i, i);// 偶数长度扩展 (中心点为i和i+1之间)int len2 = expand(s, i, i + 1);int len = Math.max(len1, len2); // 取两种扩展的最大值// 发现更长回文时更新起止位置if (len > end - start) {start = i - (len - 1) / 2;end = i + len / 2;}}return s.substring(start, end + 1);}// 中心扩展函数private int expand(String s, int left, int right) {while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {left--;right++;}return right - left - 1; // 计算实际回文长度}
}