Atto Round 1 (Codeforces Round 1041, Div. 1 + Div. 2) A-C

A. Mix Mex Max

题目大意

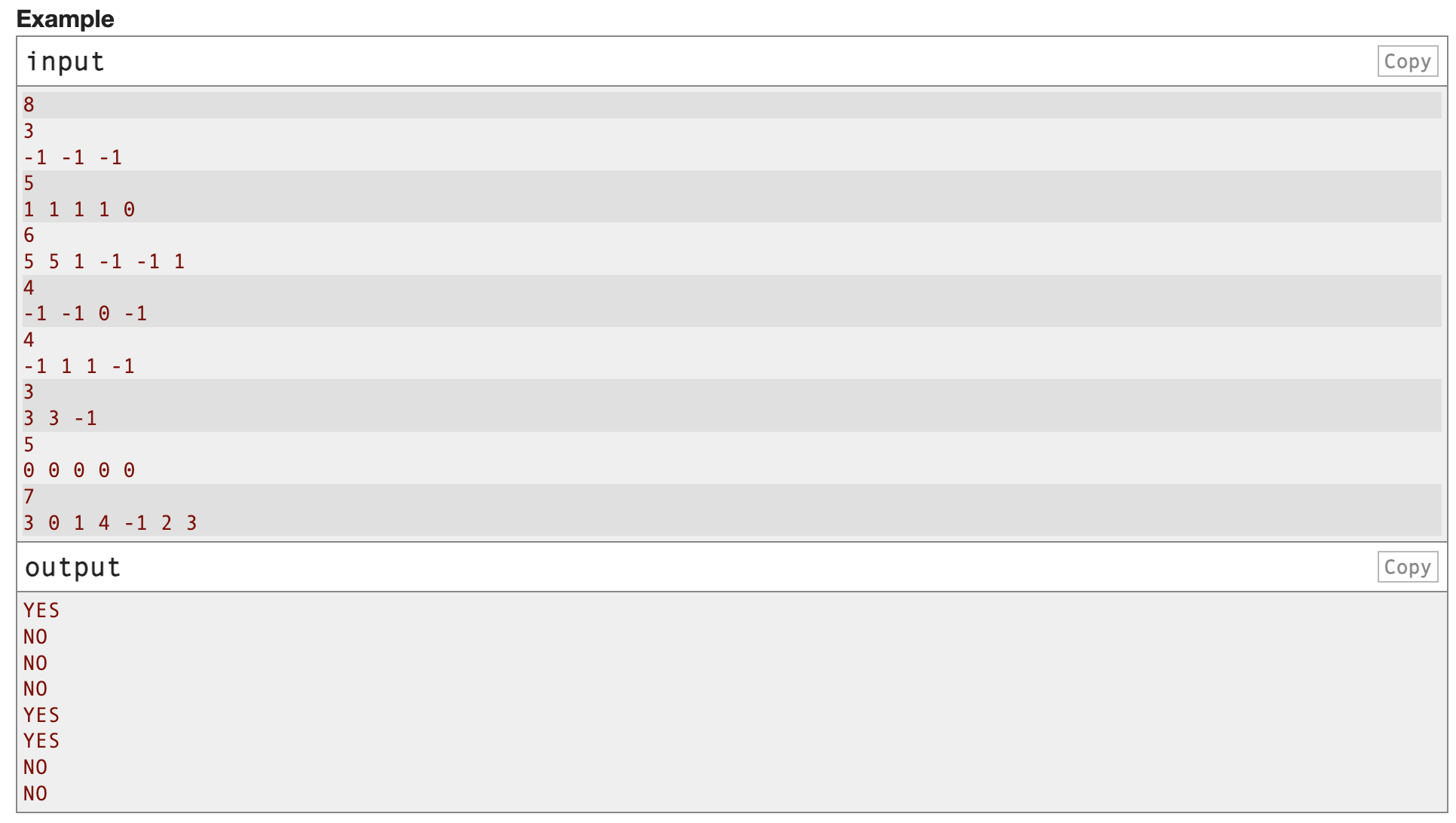
给你一个长度为n的数组，-1代表可以填充任意数字
问当-1填充后，是否存在这样的数组，使得任意三个连续的数组元素它们的max-min=mex

思路

首先数组不能出现0,如果出现0那么就变成了max=mex,这显然是不可能的
然后数组除-1以外不能出现超过一种元素，这里我们试图构造max==min,也就是三个元素都为非0的相同数，使得mex=0,max-min=0
如果有不同元素，那么max-min必然不为0，而mex不为0的条件是这三个元素中有0，和第一条又违背了
所以我们先判断数组是否有0，有0直接输出no
然后判断数组除-1以外是否最多有一种元素，有多的也输出no
其他情况输出yes

// Author: zengyz
// 2025-08-08 16:16#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;vector<int> a(n + 1);set<int> s;bool flag = false;for (int i = 1; i <= n; i++){cin >> a[i];s.insert(a[i]);if (a[i] == -1)flag = true;}for (int i = 1; i <= n; i++){if (a[i] == 0){cout << "NO" << endl;return;}}int tmp = s.size();if (flag&&s.size() == 2)tmp--;if (tmp == 1)cout << "YES" << endl;elsecout << "NO" << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

B. Hamiiid, Haaamid… Hamid?

题目大意

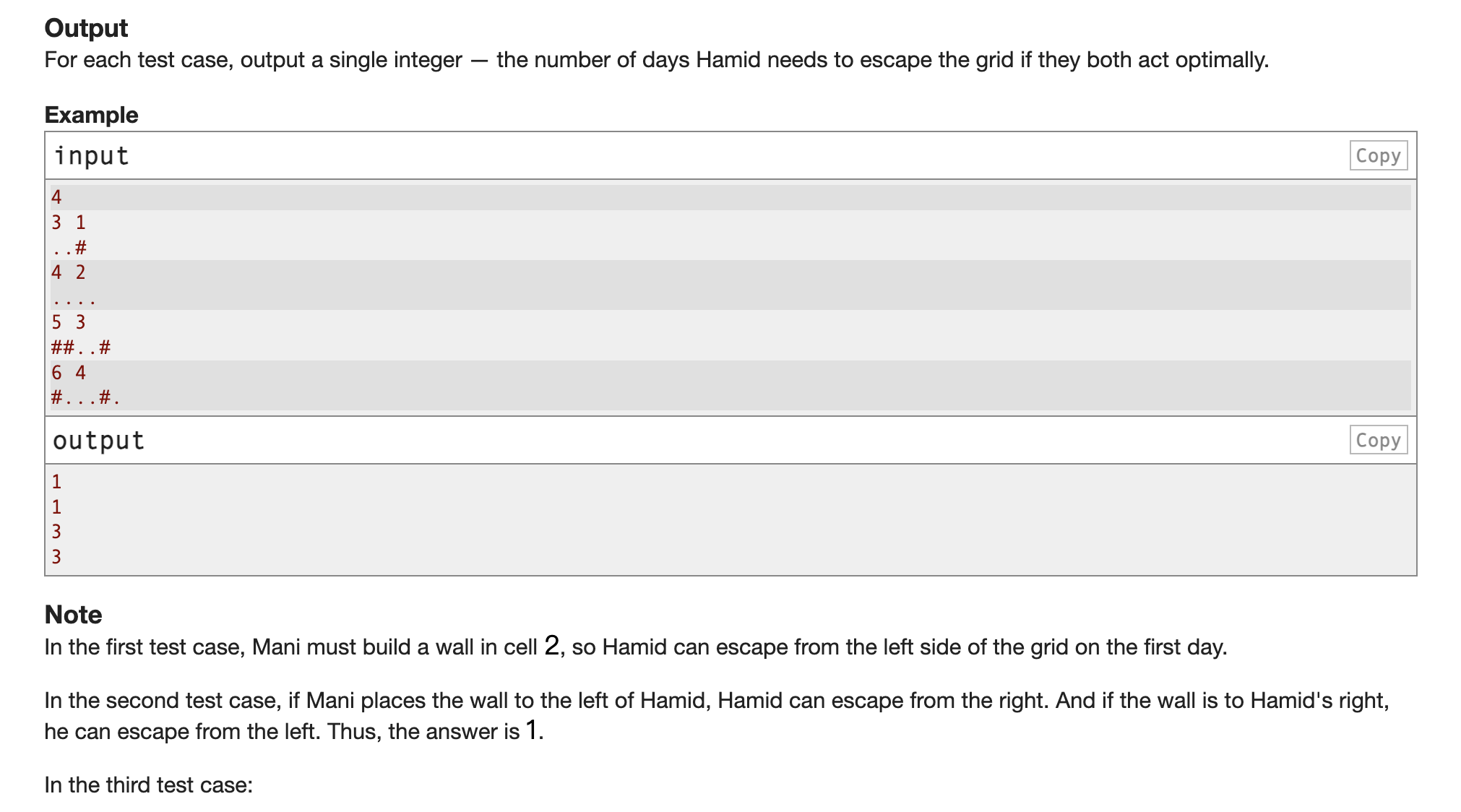
给你一个1*n的一维网格，下标1~n,有一个玩家Hamid在x位置，其中’#‘代表有一堵墙，’.'代表为空
每一天有另一个玩家Mani可以在任意空白处放一堵墙，然后Mani可以选择一个方向，移动到最近的一堵墙的位置并打破这堵墙
双方都采取最优行动，即Mani想要尽快离开这个网格，Hamid想要Mani尽可能久呆在网格内
问Hamid最少需要多少天才能离开这个网格

思路

可以想到Hamid一定是一直往一个方向走最快离开这个网格，问题就是Hamid会先选择怎么方向
定义l为最靠近x的左边的墙,l为最靠近x的右边的墙
cnt1为从1～l一共有几个格子，cnt2定义为从r~n一共有几个格子
Hamid一定会选择cnt1和cnt2中较多的一个
因为每次都是Mani先手放墙，假设cnt1<cnt2,那么Mani一定会把墙放在x-1的位置，这样Hamid想走左边就要x天，cnt1>cnt2同理需要
所以Hamid只能选择cnt1和cnt2中较多的一个，所以答案就是
$$1+max(min(x-1,cnt2),min(n-x,cnt1))$$

// Author: zengyz
// 2025-08-08 16:36#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n, x;cin >> n >> x;string s;cin >> s;s = " " + s;int cnt1 = 0;int cnt2 = 0;int l = -1;int r = n + 1;for (int i = 1; i < x; i++){if (s[i] == '#')l = max(l, i);}for (int i = x + 1; i <= n; i++){if (s[i] == '#')r = min(r, i);}cnt1 = l;cnt2 = n - r + 1;cout << 1 + max(min(x-1, cnt2), min(n - x, cnt1)) << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

C. Trip Shopping

题目大意

给你两个长度为n的数组a,b，以及数字k
有两个玩家参与一场游戏，游戏进行k轮
每一轮Ali选择两个下标i,j
Bahamin会将这两个下标对应的两个数组中的四个数位置进行任意排列（也可以不换）
Ali想要${\sum }_{i=1}^n|a_i-b_i|$尽可能小，Bahamin想要这个数尽可能大
双方都采取最优策略，问最后这个数是多少

思路

首先无论k为多少，答案都只和第一轮有关
因为Ali可以不断选择同样的下标，在第一次操作后这个数的值不会改变（因为Bahamin不可能让这个数变小，所以他不会修改排列）
然后我们考虑Ali会如何选择
其实我们可以把$a_i和b_i$抽象成一个线段[$a_i,b_i$]，那么这个下标对应的贡献就是线段的长度
那么和第j个线段[$a_j,b_j$]之间进行考虑的话（假设$a_i<a_j$)，如果这两个线段没有相交，也就是$b_i<a_j$,那么它们在Bahamin的操作下就会变成
$[a_i,a_j]$和$[b_i,b_j]$
或者
$[a_i,b_j]$和$[b_i,a_j]$
但它们的贡献都会增加$2\ast (a_j-b_i)$,也就是两个线段的距离
当然如果这两个线段已经相交了，那么贡献不会增加（当然可以把他们变成不相交，但是贡献会变小）
所以我们令$a_i$为$a_i,b_i$中的最小值,$b_i$为$a_i,b_i$中的最大值，用一个vector记录并进行递增排序（先考虑a，再考虑b)，并记录初始贡献ans
然后我们判断彼此相邻的两个“线段”之间相不相交，不相交的贡献为$2\ast (a_j-b_i)$,若有相交贡献为0
记录一个贡献最小值（最小为0），和ans相加就是答案

// Author: zengyz
// 2025-08-08 16:58#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n, k;cin >> n >> k;vector<int> a(n), b(n);for (int i = 0; i < n; i++){cin >> a[i];}for (int i = 0; i < n; i++){cin >> b[i];}ll ans = 0;vector<pair<int, int>> tmp;for (int i = 0; i < n; i++){ans += abs(a[i] - b[i]);tmp.push_back({min(a[i], b[i]), max(a[i], b[i])});}sort(tmp.begin(), tmp.end());int count=2e9;for (int i = 0; i < tmp.size() - 1; i++){count=min(count,max(0,tmp[i+1].first-tmp[i].second));}cout<<count*2+ans<<endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}