矩阵中的最长递增路径-记忆化搜索

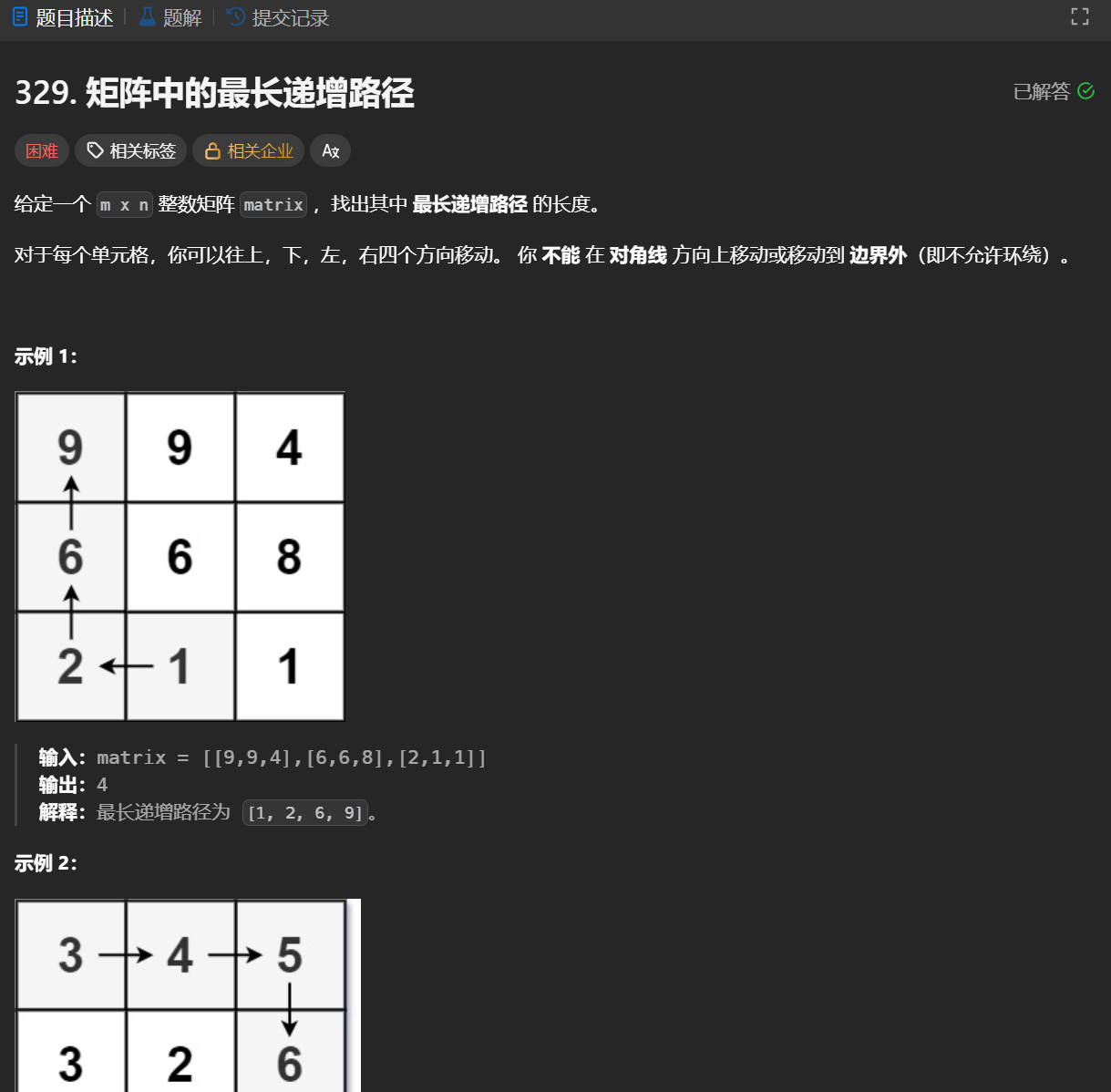
矩阵中的最长递增路径

---

Solution

一个简单的dfs搜索问题，只需要改成一个带返回值的搜索即可，再加上一个缓存表优化即可通过。

#include<iostream>
#include<vector>
using namespace std;//递归做法
//f(x,y)表示从(x,y)出发的最长递增路径长度
//由于这题的路径自带单调性，所以不需要设置标记数组
int f1(vector<vector<int>>& matrix, int x, int y) {int m = matrix.size();int n = matrix[0].size();if (x < 0 || x >= m || y < 0 || y >= n) return 0;int ans1 = 0, ans2 = 0, ans3 = 0, ans4 = 0;if (x + 1 < m && matrix[x + 1][y] > matrix[x][y]) ans1 = f1(matrix, x + 1, y);if (x - 1 >= 0 && matrix[x - 1][y] > matrix[x][y])ans2 = f1(matrix, x - 1, y);if (y + 1 < n && matrix[x][y + 1] > matrix[x][y]) ans3 = f1(matrix, x, y + 1);if (y - 1 >= 0 && matrix[x][y - 1] > matrix[x][y]) ans4 = f1(matrix, x, y - 1);return 1 + max(ans1, max(ans2, max(ans3, ans4)));
}//带缓存表的递归
int f2(vector<vector<int>>& matrix, int x, int y, vector<vector<int>>& dp) {int m = matrix.size();int n = matrix[0].size();if (x < 0 || x >= m || y < 0 || y >= n) return 0;int ans1 = 0, ans2 = 0, ans3 = 0, ans4 = 0;if (dp[x][y] != -1) return dp[x][y];if (x + 1 < m && matrix[x + 1][y] > matrix[x][y]) ans1 = f2(matrix, x + 1, y, dp);if (x - 1 >= 0 && matrix[x - 1][y] > matrix[x][y])ans2 = f2(matrix, x - 1, y, dp);if (y + 1 < n && matrix[x][y + 1] > matrix[x][y]) ans3 = f2(matrix, x, y + 1, dp);if (y - 1 >= 0 && matrix[x][y - 1] > matrix[x][y]) ans4 = f2(matrix, x, y - 1, dp);int ans = 1 + max(ans1, max(ans2, max(ans3, ans4)));dp[x][y] = ans;return ans;
}
int longestIncreasingPath1(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();int ans = 0;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {ans = max(ans, f1(matrix, i, j));}}return ans;
}
int longestIncreasingPath(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();vector<vector<int>>dp(m + 1, vector<int>(n + 1, -1));int ans = 0;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {ans = max(ans, f2(matrix, i, j, dp));}}return ans;
}int main() {return 0;
}