机器学习之支持向量机(原理)

目录

摘要

一、概述

二、SVM算法定义

1.超平⾯最⼤间隔介绍

2.硬间隔和软间隔

1.硬间隔分类

2. 软间隔分类

三、SVM算法原理

1 定义输⼊数据

2 线性可分⽀持向量机

3 SVM的计算过程与算法步骤

四、核函数

五、SVM算法api介绍

1. 核心参数说明

2. 主要方法

3. 重要属性

六、SVM支持向量机的优缺点

1、优点

2、缺点

---

摘要

支持向量机(SVM)是一种监督学习算法,用于数据的二元分类。它通过寻找最大边距超平面实现分类,适用于小样本和非线性问题。SVM能够处理线性和非线性数据,通过核函数将低维不可分数据映射到高维空间,实现线性可分。本文介绍了SVM的基本原理、硬间隔和软间隔概念、核函数以及模型评估方法。

一、概述

支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

具体来说：在线性可分时，在原空间寻找两类样本的最优分类超平面。在线性不可分时，加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。

SVM使用准则： n为特征数， m为训练样本数。

如果相较于m而言，n要大许多，即训练集数据量不够支持我们训练一个复杂的非线性模型，我们选用逻辑回归模型或者不带核函数的支持向量机。
如果 n较小，而且 m 大小中等，例如 n 在 1-1000 之间，而 m 在10-10000之间，使用高斯核函数的支持向量机。
如果 n 较小，而 m 较大，例如 n 在1-1000之间，而 m 大于50000，则使用支持向量机会非常慢，解决方案是创造、增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。

二、SVM算法定义

SVM：SVM全称是supported vector machine（⽀持向量机），即寻找到⼀个超平⾯使样本分成两类，并且间隔最 ⼤。 SVM能够执⾏线性或⾮线性分类、回归，甚⾄是异常值检测任务。它是机器学习领域最受欢迎的模型之⼀。SVM特别 适⽤于中⼩型复杂数据集的分类。

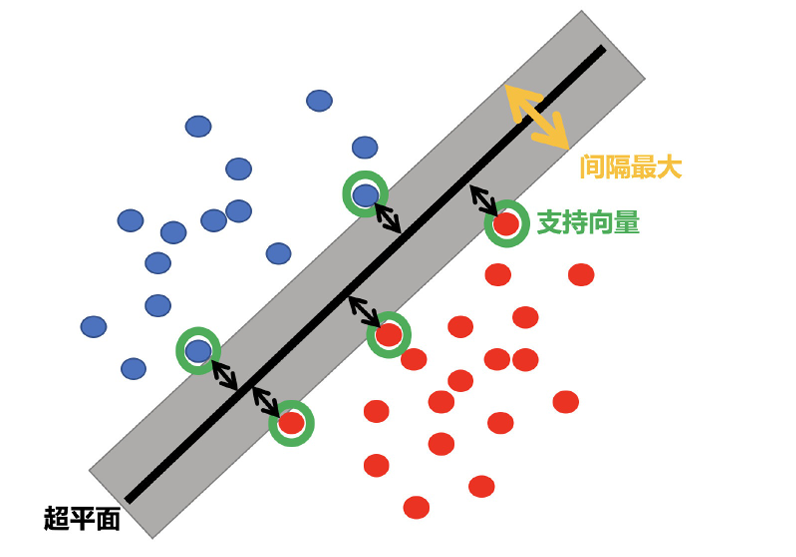
1.超平⾯最⼤间隔介绍

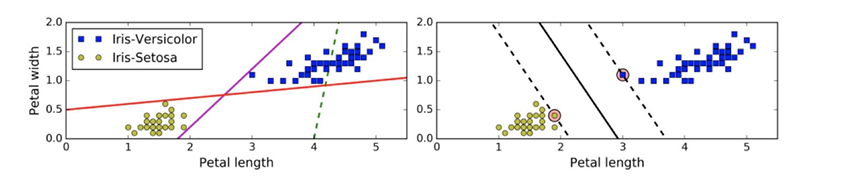上左图显示了三种可能的线性分类器的决策边界：

虚线所代表的模型表现⾮常糟糕，甚⾄都⽆法正确实现分类。其余两个模型在这个训练集上表现堪称完美，但是它们的 决策边界与实例过于接近，导致在⾯对新实例时，表现可能不会太好

右图中的实线代表SVM分类器的决策边界，不仅分离了两个类别，且尽可能远离最近的训练实例。

2.硬间隔和软间隔

1.硬间隔分类

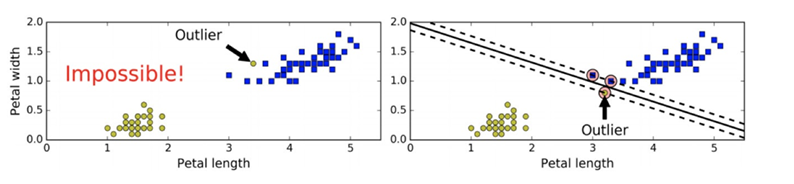
在上⾯我们使⽤超平⾯进⾏分割数据的过程中，如果我们严格地让所有实例都不在最⼤间隔之间，并且位于正确的⼀ 边，这就是硬间隔分类。 硬间隔分类有两个问题，⾸先，它只在数据是线性可分离的时候才有效；其次，它对异常值⾮常敏感。 当有⼀个额外异常值的鸢尾花数据：左图的数据根本找不出硬间隔，⽽右图最终显示的决策边界与我们之前所看到的⽆ 异常值时的决策边界也⼤不相同，可能⽆法很好地泛化

2. 软间隔分类

要避免这些问题，最好使⽤更灵活的模型。⽬标是尽可能在保持最⼤间隔宽阔和限制间隔违例（即位于最⼤间隔之上， 甚⾄在错误的⼀边的实例）之间找到良好的平衡，这就是软间隔分类。 要避免这些问题，最好使⽤更灵活的模型。⽬标是尽可能在保持间隔宽阔和限制间隔违例之间找到良好的平衡，这就是 软间隔分类

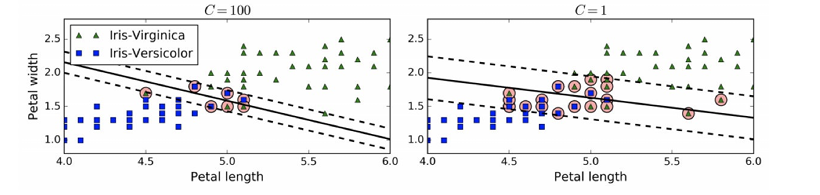
在Scikit-Learn的SVM类中，可以通过超参数C来控制这个平衡：C值越⼩，则间隔越宽，但是间隔违例也会越多。上图 显示了在⼀个⾮线性可分离数据集上，两个软间隔SVM分类器各⾃的决策边界和间隔。

左边使⽤了⾼C值，分类器的错误样本（间隔违例）较少，但是间隔也较⼩。

右边使⽤了低C值，间隔⼤了很多，但是位于间隔上的实例也更多。

看起来第⼆个分类器的泛化效果更好，因为⼤多数 间隔违例实际上都位于决策边界正确的⼀边，所以即便是在该训练集上，它做出的错误预测也会更少。

三、SVM算法原理

1 定义输⼊数据

假设给定⼀个特征空间上的训练集为：

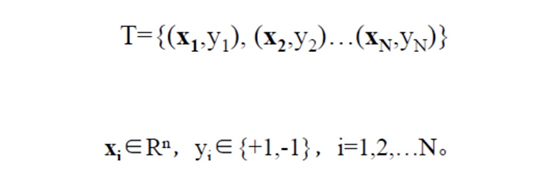
其中，(xi,yi )称为样本点。

xi 为第i个实例（样本）， yi 为xi的标记：当yi =1时，xi为正例 当yi =−1时，xi为负例 

2 线性可分⽀持向量机

给定了上⾯提出的线性可分训练数据集，通过间隔最⼤化得到分离超平⾯为 :y(x)=wT Φ(x)+b T 相应的分类决策函数为： f(x)=sign(wT Φ(x)+b) 以上决策函数就称为线性可分⽀持向量机。

这⾥解释⼀下Φ(x)这个东东。 i这是某个确定的特征空间转换函数，它的作⽤是将x映射到更⾼的维度，它有⼀个以后我们经常会⻅到的专有称号”核函 数“。

以上就是线性可分⽀持向量机的模型表达式。我们要去求出这样⼀个模型，或者说这样⼀个超平⾯y(x),它能够最优地分 离两个集合。 其实也就是我们要去求⼀组参数（w,b),使其构建的超平⾯函数能够最优地分离两个集合。 如下就是⼀个最优超平⾯:

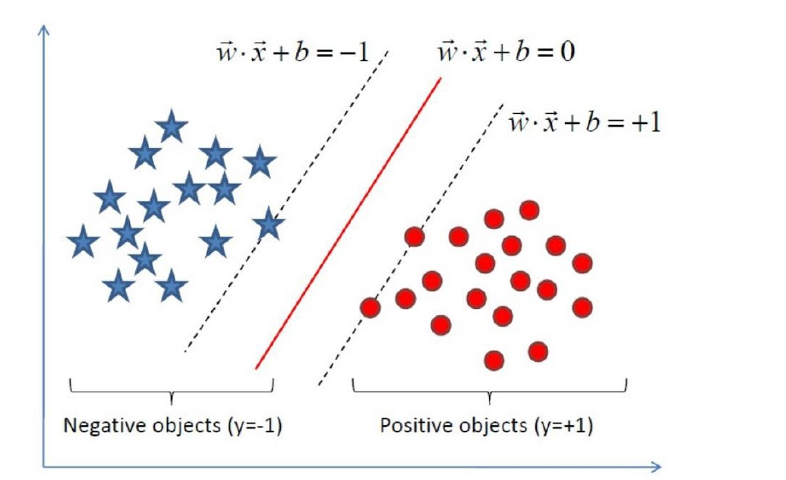
3 SVM的计算过程与算法步骤

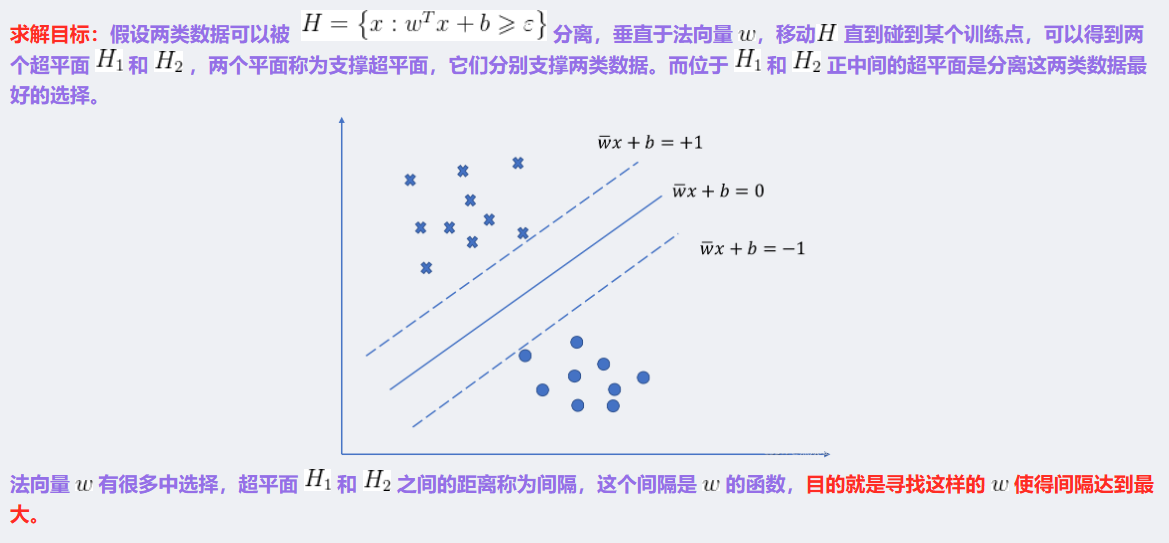
对偶问题

四、核函数

支持向量机算法分类和回归方法的中都支持线性性和非线性类型的数据类型。非线性类型通常是二维平面不可分，为了使数据可分，需要通过一个函数将原始数据映射到高维空间，从而使得数据在高维空间很容易可分，需要通过一个函数将原始数据映射到高维空间，从而使得数据在高维空间很容易区分，这样就达到数据分类或回归的目的，而实现这一目标的函数称为核函数。

工作原理：当低维空间内线性不可分时，可以通过高位空间实现线性可分。但如果在高维空间内直接进行分类或回归时，则存在确定非线性映射函数的形式和参数问题，而最大的障碍就是高维空间的运算困难且结果不理想。通过核函数的方法，可以将高维空间内的点积运算，巧妙转化为低维输入空间内核函数的运算，从而有效解决这一问题。

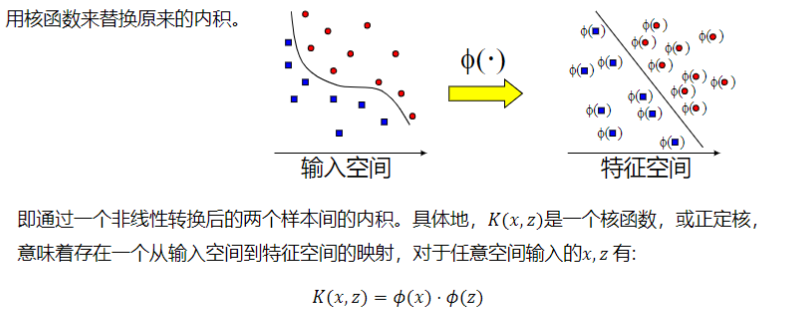
常见的核函数：

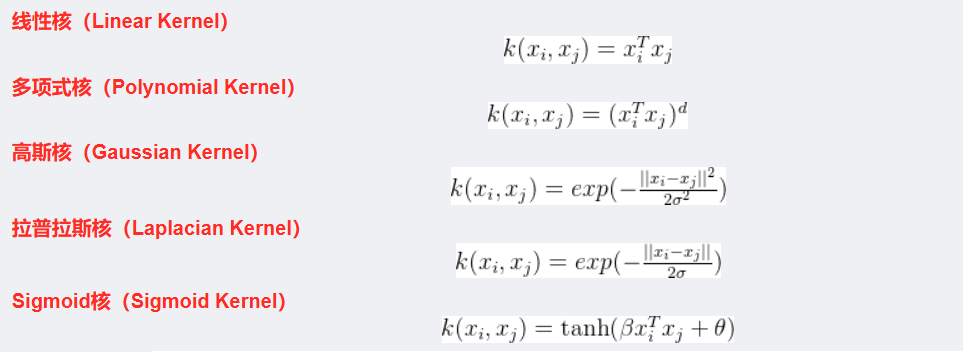
五、SVM算法api介绍

SVC(kernel='rbf', C=1.0, gamma='scale', degree=3, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)

• 1. 核心参数说明

• kernel：核函数类型，决定数据映射到高维空间的方式

  'linear'：线性核（默认用于线性可分数据）
• 'rbf'：径向基函数（默认值，适用于非线性数据，需配合gamma调整）
• 'poly'：多项式核（参数degree控制阶数）
• 'sigmoid'：Sigmoid 核

• C：正则化参数（默认 1.0）

  控制对误分类的惩罚程度，C越大，模型对训练集拟合越严格（可能过拟合）；C越小，容错性越强（可能欠拟合）。

• gamma：核系数（仅对rbf、poly、sigmoid有效）

  'scale'（默认）：1/(n_features * X.var())
• 'auto'：1/n_features
• 数值越大，核函数作用范围越小（可能过拟合）；反之则作用范围广（可能欠拟合）。

• degree：多项式核的阶数（默认 3），仅当kernel='poly'时有效。

• class_weight：类别权重（用于不平衡数据）

  None（默认）：所有类别权重相同
• 'balanced'：根据训练样本比例自动计算权重（n_samples / (n_classes * np.bincount(y))）

2. 主要方法

• fit(X, y)：训练模型

  X：特征数据（形状为[n_samples, n_features]）
• y：标签数据（形状为[n_samples]）

• predict(X)：预测新样本类别

  返回预测标签数组（形状为[n_samples]）

• predict_proba(X)：预测每个类别的概率（需设置probability=True）

  返回概率矩阵（形状为[n_samples, n_classes]）

• score(X, y)：计算模型在X和y上的准确率（accuracy）

• decision_function(X)：返回样本到决策边界的距离（用于获取支持向量等）

3. 重要属性

• support_vectors_：训练集中的支持向量
• coef_：线性核的权重系数（仅当kernel='linear'时有效）
• intercept_：线性核的偏置项
• n_support_：每个类别的支持向量数量

六、SVM支持向量机的优缺点

1、优点

1. 良好的泛化能力
   SVM 的核心思想是寻找 “最大间隔超平面”，通过最大化类别间的间隔，使模型对未知数据具有较强的泛化能力，尤其在小样本数据集上表现出色。

2. 适用于高维空间
   即使特征维度高于样本数量，SVM 仍能有效工作（例如文本分类中，特征维度常远大于样本数），因为它无需依赖数据的维度规模，而是通过核函数处理高维映射。

3. 通过核函数处理非线性问题
   借助核函数（如 RBF、多项式核等），SVM 可以将低维非线性可分的数据映射到高维空间，转化为线性可分问题，灵活处理非线性分类任务。

4. 对噪声不敏感（一定程度上）
   通过引入正则化参数C，SVM 可以控制对噪声的容忍度，平衡间隔最大化和分类错误最小化，避免过度拟合噪声数据。

5. 决策边界清晰
   最终的决策边界仅由支持向量决定，无需依赖全部样本，计算复杂度不随样本数量激增而大幅上升（尤其在核函数为线性时）。

2、缺点

1. 对大规模数据集效率较低
   SVM 的训练过程涉及求解凸二次规划问题，时间复杂度较高（通常为O(n3)，n为样本数），在百万级以上样本的数据集上训练速度较慢。

2. 对参数和核函数选择敏感
   模型性能高度依赖于核函数类型（如线性核、RBF 核）和参数（如C、核函数参数γ）的选择，需要通过交叉验证等方法调参，过程较繁琐。

3. 不适用于多类别问题（原生支持二分类）
   SVM 原生仅支持二分类任务，处理多类别问题时需通过 “一对多”（One-vs-Rest）或 “一对一”（One-vs-One）等策略转换，增加了计算复杂度。

4. 对缺失数据敏感
   SVM 假设数据是完整的，对缺失值较为敏感，需要先对数据进行预处理（如填充缺失值），否则会影响模型性能。

5. 结果解释性较差
   与决策树等模型不同，SVM 的决策边界由支持向量和核函数共同决定，难以直观解释特征对分类结果的影响，缺乏可解释性。