当前位置：首页 > news >正文

机械学习--SVM 算法

news 2025/8/9 5:50:47

一、svm的数学基础

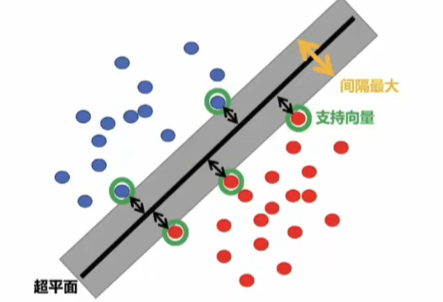
支持向量机（SVM）的硬间隔数学推导旨在找到线性可分数据的最优超平面，最大化分类间隔。以下是关键步骤的详细推导：

一、问题定义

给定线性可分的训练集 $\{(\mathbf{x}_i, y_i)\}_{i=1}^n$ ，其中 $\mathbf{x}_i \in \mathbb{R}^d$ 是特征向量， $y_i \in \{-1, 1\}$ 是类别标签。超平面方程为： $\mathbf{w}^\top \mathbf{x} + b = 0$ 其中 $\mathbf{w}$ 是法向量，b 是截距。分类决策函数为 $f(\mathbf{x}) = \text{sign}(\mathbf{w}^\top \mathbf{x} + b)$ 。

二、间隔最大化

1. 几何间隔与函数间隔

样本 $\mathbf{x}_i$ 到超平面的几何间隔为： $\gamma_i = \frac{y_i (\mathbf{w}^\top \mathbf{x}_i + b)}{\|\mathbf{w}\|}$ 函数间隔为 $y_i (\mathbf{w}^\top \mathbf{x}_i + b)$ 。为满足分类正确性，要求所有样本的函数间隔至少为 1： $y_i (\mathbf{w}^\top \mathbf{x}_i + b) \geq 1, \quad \forall i$

2. 优化目标

最大化几何间隔等价于最小化 $\frac{1}{2}\|\mathbf{w}\|^2$ （平方简化求导），约束条件为： $y_i (\mathbf{w}^\top \mathbf{x}_i + b) \geq 1, \quad \forall i$ 即原问题：

$\min_{\mathbf{w}, b} \frac{1}{2}\|\mathbf{w}\|^2 \quad \text{s.t.} \quad y_i (\mathbf{w}^\top \mathbf{x}_i + b) \geq 1, \, \forall i$

三、拉格朗日对偶问题

1. 构造拉格朗日函数

引入拉格朗日乘子 $\alpha_i \geq 0$ ，构造拉格朗日函数：

$\mathcal{L}(\mathbf{w}, b, \alpha) = \frac{1}{2}\|\mathbf{w}\|^2 - \sum_{i=1}^n \alpha_i \left( y_i (\mathbf{w}^\top \mathbf{x}_i + b) - 1 \right)$

2. 求偏导并消元

对 $\mathbf{w}$ 和 b 求偏导并令其为零：

$\frac{\partial \mathcal{L}}{\partial \mathbf{w}} = \mathbf{w} - \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i = 0 \quad \Rightarrow \quad \mathbf{w} = \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i \quad \text{(1)}$

$\frac{\partial \mathcal{L}}{\partial b} = -\sum_{i=1}^n \alpha_i y_i = 0 \quad \Rightarrow \quad \sum_{i=1}^n \alpha_i y_i = 0 \quad \text{(2)}$

3. 对偶问题转换

将式（1）和（2）代入拉格朗日函数，消去 $\mathbf{w}$ 和 b，得到仅关于 $\alpha$ 的对偶问题：

$\max_{\alpha} \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j (\mathbf{x}_i^\top \mathbf{x}_j)$

约束条件为：

$\sum_{i=1}^n \alpha_i y_i = 0, \quad \alpha_i \geq 0, \, \forall i$

四、求解对偶问题

1. KKT 条件

最优解 $\alpha^*$ 满足 KKT 条件：

原始约束： $y_i (\mathbf{w}^\top \mathbf{x}_i + b) \geq 1$
对偶约束： $\alpha_i \geq 0$
互补松弛： $\alpha_i (y_i (\mathbf{w}^\top \mathbf{x}_i + b) - 1) = 0$
梯度条件： $\mathbf{w} = \sum_{i=1}^n \alpha_i y_i \mathbf{x}_i$ 和 $\sum_{i=1}^n \alpha_i y_i = 0$

2. 支持向量确定

根据互补松弛条件，当 $\alpha_i > 0$ 时，对应样本满足 $y_i (\mathbf{w}^\top \mathbf{x}_i + b) = 1$ ，即这些样本位于间隔边界上，称为支持向量。

五、参数计算

1. 求解 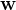$\mathbf{w}$

由式（1）得： $\mathbf{w}^* = \sum_{i=1}^n \alpha_i^* y_i \mathbf{x}_i$ 仅支持向量对应的 $\alpha_i^* > 0$ ，非支持向量的 $\alpha_i^* = 0$ ，因此 $\mathbf{w}^*$ 由支持向量线性组合而成。

2. 求解 b

对任意支持向量 $\mathbf{x}_s$ ，代入 $y_s (\mathbf{w}^* \top \mathbf{x}_s + b^*) = 1$ ： $(b^* = y_s - \mathbf{w}^{*\top} \mathbf{x}_s$ 通常取所有支持向量计算的 $b^*$ 的平均值以提高稳定性。

六、最终模型

分类决策函数为： $f(\mathbf{x}) = \text{sign}\left( \sum_{i \in S} \alpha_i^* y_i (\mathbf{x}_i^\top \mathbf{x}) + b^* \right)$ 其中 S 是支持向量的下标集合。

七、硬间隔 SVM 基础应用

给定线性可分训练集：正类样本 $\mathbf{x}_1=(3,3), y_1=1$ ； $\mathbf{x}_2=(4,3), y_2=1$ ；负类样本 $\mathbf{x}_3=(1,1), y_3=-1$ 。请使用硬间隔 SVM 求解最优超平面方程 $f(\mathbf{x})=\mathbf{w}^\top \mathbf{x} + b = 0$ ，并回答以下问题：
（1）确定支持向量；
（2）计算参数 $\mathbf{w}$ 和 b；
（3）写出分类决策函数。

解答步骤

步骤 1：理解硬间隔 SVM 的核心约束

硬间隔 SVM 要求所有样本被正确分类，且距离超平面的函数间隔至少为 1，即：

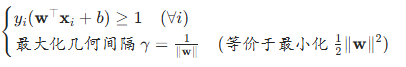
步骤 2：确定支持向量

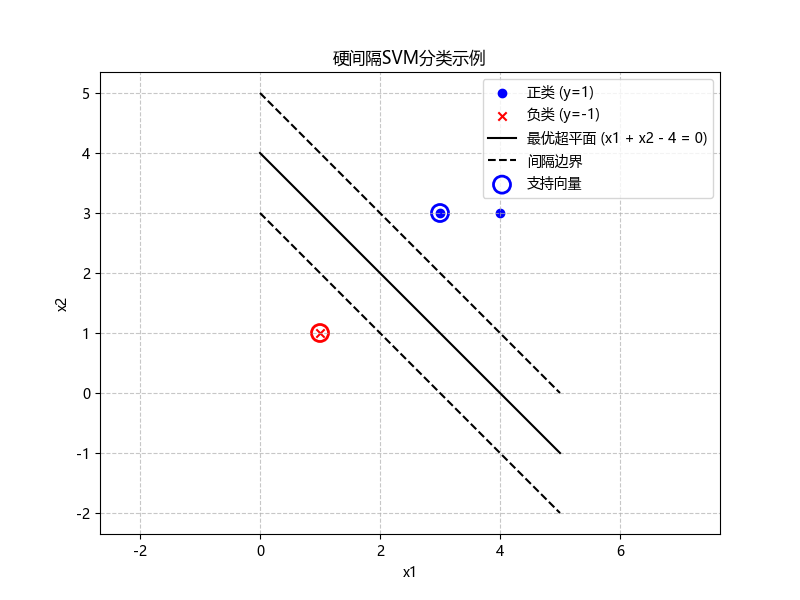
支持向量是满足 $y_i (\mathbf{w}^\top \mathbf{x}_i + b) = 1$ 的样本（位于间隔边界上）。观察数据分布：

正类样本 (3,3)、(4,3) 较近，负类样本 (1,1) 单独分布，直观上最优超平面应在两类中间，间隔边界可能由正类中离负类最近的点和负类点构成。

假设支持向量为 $\mathbf{x}_1=(3,3)$ （正类）和 $\mathbf{x}_3=(1,1)$ （负类），则它们满足：

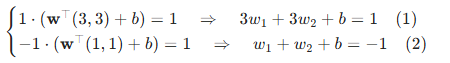
步骤 3：求解参数 $\mathbf{w}$ 和 b

（1）消去 b：用式 (1) 减式 (2)：

$(3w_1 + 3w_2 + b) - (w_1 + w_2 + b) = 1 - (-1) \quad \Rightarrow \quad 2w_1 + 2w_2 = 2 \quad \Rightarrow \quad w_1 + w_2 = 1 \quad (3)$

（2）代入 b 表达式：由式 (2) 得 $b = -1 - w_1 - w_2$ ，结合式 (3) 中 $w_1 + w_2 = 1$ ，得 $b = -1 - 1 = -2$ 。

（3）最小化 $\frac{1}{2}\|\mathbf{w}\|^2$ ：目标函数为 $\frac{1}{2}(w_1^2 + w_2^2)$ ，结合 $w_2 = 1 - w_1$ （由式 (3)），

代入得： $\frac{1}{2}(w_1^2 + (1 - w_1)^2) = \frac{1}{2}(2w_1^2 - 2w_1 + 1)$

对 $w_1$ 求导并令导数为 0： $2w_1 - 1 = 0 \Rightarrow w_1 = 0.5$ ，则 $w_2 = 1 - 0.5 = 0.5$ 。

（4）验证约束：检查非支持向量 $\mathbf{x}_2=(4,3)$ 是否满足

$y_2 (\mathbf{w}^\top \mathbf{x}_2 + b) \geq 1$

$1 \cdot (0.5 \times 4 + 0.5 \times 3 - 2) = 1 \cdot (2 + 1.5 - 2) = 1.5 \geq 1$ （满足约束）

步骤 4：结论

（1）支持向量： $\mathbf{x}_1=(3,3)$ 和 $\mathbf{x}_3=(1,1)$ （仅这两个样本满足 $y_i (\mathbf{w}^\top \mathbf{x}_i + b) = 1$ ）。

（2）参数： $\mathbf{w} = (0.5, 0.5)$ ，b = -2。

（3）分类决策函数：

$f(\mathbf{x}) = \text{sign}(0.5x_1 + 0.5x_2 - 2) = \text{sign}(x_1 + x_2 - 4)$ （两边同乘2不改变符号）

答案总结：

（1）支持向量为 (3,3) 和 (1,1)；

（2） $\mathbf{w} = (0.5, 0.5)$ ，b=−2；

（3）决策函数为 $f(\mathbf{x}) = \text{sign}(x_1 + x_2 - 4)$ 。

二、svm的代码实现

svc_default = SVC(C=1.0,                  # 正则化参数，默认1.0kernel='rbf',           # 核函数类型，默认'rbf'degree=3,               # 多项式核的阶数，默认3（仅对poly核有效）gamma='scale',          # 核系数，默认'scale'（对rbf, poly, sigmoid有效）coef0=0.0,              # 核函数常数项，默认0.0（对poly和sigmoid有效）shrinking=True,         # 是否使用收缩启发式，默认Trueprobability=False,      # 是否启用概率估计，默认Falsetol=1e-3,               # 收敛容差，默认1e-3cache_size=200,         # 缓存大小(MB)，默认200class_weight=None,      # 类别权重，默认Noneverbose=False,          # 是否输出详细信息，默认Falsemax_iter=-1,            # 最大迭代次数，默认-1（无限制）decision_function_shape='ovr',  # 多类决策函数形状，默认'ovr'break_ties=False,       # 是否打破平局，默认False（scikit-learn 0.22+新增）random_state=None       # 随机数种子，默认None
)

1. 核心参数（控制模型结构与优化目标）

C：
类型：float，默认值：1.0
意义：正则化参数，控制对误分类样本的惩罚力度。C值越小，正则化越强（允许更多误分类，模型更简单，避免过拟合）；C值越大，正则化越弱（尽可能减少误分类，可能导致过拟合）。
kernel：
类型：str，默认值：'rbf'
意义：指定核函数类型，用于将低维数据映射到高维空间以解决非线性问题。可选值：
- 'linear'：线性核函数，适用于线性可分数据，计算速度快。
- 'poly'：多项式核函数，适用于中等复杂度数据。
- 'rbf'：径向基函数（高斯核），适用于非线性数据，默认值，通用性强。
- 'sigmoid'：Sigmoid 核函数，类似神经网络的激活函数。
- 'precomputed'：预计算核矩阵（需手动输入核矩阵，形状为(n_samples, n_samples)）。
degree：
类型：int，默认值：3
意义：仅当kernel='poly'时有效，指定多项式核函数的阶数。阶数越高，模型复杂度越高，可能过拟合。
gamma：
类型：str 或 float，默认值：'scale'
意义：核系数，仅对rbf、poly、sigmoid核有效。控制核函数的 “影响范围”：
- 'scale'（默认）：随数据特征缩放自动调整。
- 'auto'：仅与特征数量相关。
- 手动指定 float 值：值越小，核函数影响范围越大（模型更简单）；值越大，影响范围越小（模型更复杂，易过拟合）。
coef0：
类型：float，默认值：0.0
意义：核函数中的常数项，仅对poly和sigmoid核有效。影响低阶项在核函数中的权重，对多项式核可理解为 “偏置”。

2. 优化与训练参数（控制训练过程）

tol：
类型：float，默认值：1e-3
意义：训练停止的容差。当迭代过程中损失函数的变化小于tol时，视为收敛并停止训练。
cache_size：
类型：float，默认值：200
意义：指定核函数缓存的大小（单位：MB）。增大缓存可加速训练（尤其数据量大时），但需更多内存。
max_iter：
类型：int，默认值：-1
意义：最大迭代次数。-1 表示无限制（直到收敛）；指定正数时，达到次数后强制停止（可能未收敛）。
shrinking：
类型：bool，默认值：True
意义：是否使用 “收缩启发式”。开启后，算法会动态忽略对决策边界无影响的样本（非支持向量），加速训练。
verbose：
类型：bool，默认值：False
意义：是否输出训练过程的详细信息（如迭代次数、损失变化等）。需注意，多线程情况下可能无法正常输出。

3. 多类分类与类别不平衡参数

decision_function_shape：
类型：str 或 None，默认值：'ovr'
意义：指定多类分类的决策函数形状。可选值：
- 'ovr'（默认）：“一对多” 策略，为每个类别训练一个二分类器（区分该类与其他所有类）。
- 'ovo'：“一对一” 策略，为每对类别训练一个二分类器，最终通过投票决定类别。
- None：返回原始决策函数（与kernel='linear'结合时常用）。
class_weight：
类型：dict、str 或 None，默认值：None
意义：指定类别权重，用于处理不平衡数据集。可选值：
- None：所有类别权重为 1（默认）。
- 'balanced'：自动根据训练样本中各类别的频率调整权重（权重与类别频率成反比）。
- dict：手动指定，如{0: 0.5, 1: 2.0}表示类别 0 的权重为 0.5，类别 1 为 2.0。

4. 其他参数

probability：
类型：bool，默认值：False
意义：是否启用概率估计。若为 True，训练结束后可通过predict_proba()输出样本属于各类别的概率（需额外进行 5 折交叉验证，会增加训练时间）。
random_state：
类型：int、RandomState 实例或 None，默认值：None
意义：控制随机性。当shrinking=True或probability=True时，算法存在随机性，指定固定值可保证结果可复现。
break_ties：
类型：bool，默认值：False（scikit-learn 0.22 + 新增）
意义：当多类分类中出现预测分数相等（平局）时，是否打破平局。若为 True，将使用decision_function的置信度进一步判断；若为 False，则返回索引较小的类别。

三、实战案例

这里用经典的鸢尾花的数据集来展示，数据集已经上传可自行下载

1. 导入所需库

import pandas as pd
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt

pandas: 用于数据读取和数据处理操作
SVC: 从 scikit-learn 库导入支持向量机分类器
numpy: 用于数值计算和数组操作
matplotlib.pyplot: 用于数据可视化和绘图

2. 设置中文显示

plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

font.sans-serif: 设置默认字体为微软雅黑，确保中文能正常显示
axes.unicode_minus: 解决负号显示异常的问题（避免负号显示为方块）

3. 数据读取与预处理

date = pd.read_csv('iris.csv')
x = date.iloc[:, 1:3]
y = date.iloc[:, -1]

读取鸢尾花数据集 (iris.csv)，这是一个经典的分类数据集
x = date.iloc[:, 1:3]: 选取数据集中第 2 列到第 3 列作为特征数据（通常是花萼长度和宽度）
y = date.iloc[:, -1]: 选取最后一列作为目标变量（花的类别标签）

4. 构建并训练 SVM 模型

svm = SVC(kernel='linear', C=1, random_state=0)
svm.fit(x, y)

创建 SVM 分类器实例：
- kernel='linear': 使用线性核函数，适用于线性可分的数据
- C=1: 正则化参数，控制惩罚项的强度，值越大对错误分类的惩罚越重
- random_state=0: 设置随机种子，保证结果可复现
svm.fit(x, y): 用特征数据 x 和标签 y 训练 SVM 模型

5. 获取模型参数

w = svm.coef_[0]
b = svm.intercept_[0]

w = svm.coef_[0]: 获取 SVM 模型的权重系数（系数向量）
b = svm.intercept_[0]: 获取 SVM 模型的偏置项（截距）
这些参数用于后续计算决策边界

6. 生成决策边界的 x 坐标范围

x1 = np.linspace(0, 7, 300)

使用np.linspace在 0 到 7 之间生成 300 个均匀分布的点
这些点将作为 x 轴坐标，用于绘制决策边界

7. 计算决策边界和支持向量边界

# 修正决策边界计算
x2 = -(w[0] * x1 + b) / w[1]# 修正支持向量边界计算公式
x3 = -(w[0] * x1 + b - 1) / w[1]
x4 = -(w[0] * x1 + b + 1) / w[1]

决策边界公式推导自 SVM 的分类超平面方程w[0]*x1 + w[1]*x2 + b = 0，求解得到 x2 关于 x1 的表达式
x3和x4是支持向量所在的边界线，分别对应w[0]*x1 + w[1]*x2 + b = 1和w[0]*x1 + w[1]*x2 + b = -1

8. 数据可视化

date1 = date.iloc[:50, :]
date2 = date.iloc[50:, :]
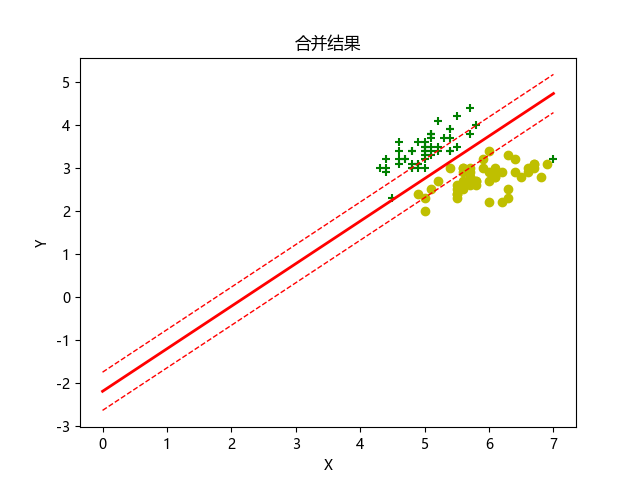
plt.scatter(date1.iloc[:, 1], date1.iloc[:, 2], marker='+', color='g')
plt.scatter(date2.iloc[:, 1], date2.iloc[:, 2], marker='o', color='y')

将数据分为两部分（前 50 条和剩余数据）
使用散点图绘制两类数据：
- 第一类用绿色 "+" 标记
- 第二类用黄色 "o" 标记
- 横轴和纵轴分别对应之前选取的两个特征

9. 绘制决策边界

plt.plot(x1, x2, linewidth=2, color='r')
plt.plot(x1, x3, linewidth=1, color='r', linestyle='--')
plt.plot(x1, x4, linewidth=1, color='r', linestyle='--')

绘制红色实线作为决策边界（x2）
绘制红色虚线作为支持向量边界（x3 和 x4）

10. 设置图表属性并显示

plt.title("合并结果")
plt.xlabel("X")
plt.ylabel("Y")# 添加显示语句，否则可能不显示图像
plt.show()

设置图表标题为 "合并结果"
设置 x 轴和 y 轴标签
plt.show(): 显示绘制的图表

11. 完整代码

import pandas as pd
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
date = pd.read_csv('iris.csv')
x = date.iloc[:, 1:3]
y = date.iloc[:, -1]
svm = SVC(kernel='linear', C=1, random_state=0)
svm.fit(x, y)
w = svm.coef_[0]
b = svm.intercept_[0]
x1 = np.linspace(0, 7, 300)
# 修正决策边界计算
x2 = -(w[0] * x1 + b) / w[1]
# 修正支持向量边界计算公式
x3 = -(w[0] * x1 + b - 1) / w[1]
x4 = -(w[0] * x1 + b + 1) / w[1]
date1 = date.iloc[:50, :]
date2 = date.iloc[50:, :]
plt.scatter(date1.iloc[:, 1], date1.iloc[:, 2], marker='+', color='g')
plt.scatter(date2.iloc[:, 1], date2.iloc[:, 2], marker='o', color='y')
plt.plot(x1, x2, linewidth=2, color='r')
plt.plot(x1, x3, linewidth=1, color='r', linestyle='--')
plt.plot(x1, x4, linewidth=1, color='r', linestyle='--')
plt.title("合并结果")
plt.xlabel("X")
plt.ylabel("Y")
# 添加显示语句，否则可能不显示图像
plt.show()

运行结果