LeetCode有效三角形的个数

有效三角形个数

• 有效三角形的个数

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

本题首先需要发现一个规律，就是当你的三条边(a,b,c)长度按升序排列的时候，只需要验证a+b>c即可验证能否构成三角形，因为a+b>c则a+c>b，且b+c>a，那么这个时候可以暴力解法，直接先确定一条边开始选择另外两个边，时间复杂度O(n^3)。

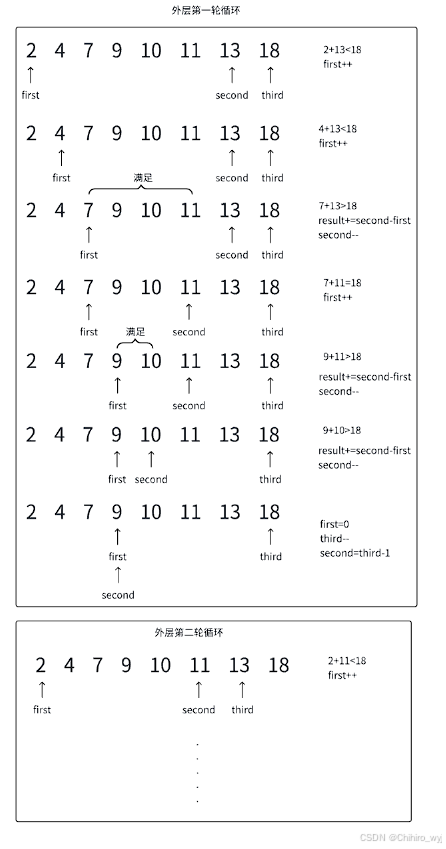
本题巧妙的解法可以利用排序后的单调性使用双指针，初始first=0，third=nums.size()-1，second=third-1，固定third这条边，去找另外两条边，当nums[first]+nums[second]>nums[third]之后，则first和second之间的所有元素都可以满足条件，因为中间的元素一定都比nums[first]大，一定满足不等式，当nums[first]+nums[second]<nums[third]的时候，只需要将first++，直到nums[first]+nums[second]>nums[third]，每次找到满足条件的first之后，second，result+=second-first，直到second<first，first不用变，因为当second--之后当前second所指向的值一定是比之前小或者相等的，那么如果first减小的情况下，则nums[first]减小，nums[second]减小，而一轮循环后first又是刚好满足nums[first]+nums[second]>nums[third]的最小值，那么就不可能满足条件。当second<first之后third--，first=0，second=third-1，进行最外层新一轮循环。

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int n=nums.size();int first=0;int third=n-1;int second=third-1;int result=0;if(n<3){return result;}while(third>=2){while(first<second){if(nums[first]+nums[second]>nums[third]){result+=second-first;second--;}else{first++;}}third--;first=0;second=third-1;}return result;}
};