Linux学习-数据结构（二叉树）

1.概念

• 线性结构：描述数据一对一（表）的关系
• 非线性结构：描述数据一对多（树），多对多（图）的关系

2.树形结构

• 节点：树形结构中组成树形结构的一个小的单元称为节点
• 前驱（祖先）：由哪个节点可以访问到该节点
• 后继（子孙）：该节点可以后续访问到哪些节点
• 层：根节点层数为1，后续每引申出来一个节点，层数+1
• 树的层数：由层数最高的节点对应的层数表示树的层数
• 高度：节点高度是由该节点到最远的叶子节点的距离表示该节点高度
• 深度：节点深度由该节点到根节点的距离表示节点深度
• 树的高度 == 树的深度 == 树的层数
• 度：后继节点的个数

节点：

• 根节点：只有后继没有前驱
• 分支节点：既有前驱也有后继
• 叶子节点：只有前驱没有后继

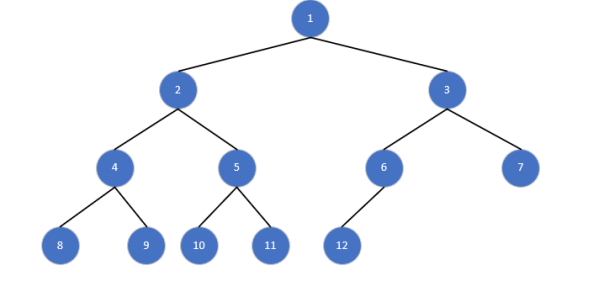
3.二叉树

1.概念

树型结构中的所有节点度数最大为2，称为二叉树

2.二叉树节点状态

• 叶子节点：度数为0
• 只有左孩子
• 只有右孩子
• 左右孩子都有

3.满二叉树

所以的叶子节点均在同一层，且每层节点个数均为最大值

---

特性：

• 满二叉树第k层节点有
• 满二叉树前k层节点有

4.完全二叉树

二叉树的编号（如果节点编号为n，左孩子编号为2n，右孩子编号为2n+1）展开是连续的，称为完全二叉树

---

二叉树的遍历形式

• 深度优先遍历（DFS）
• 广度优先遍历（BFS）

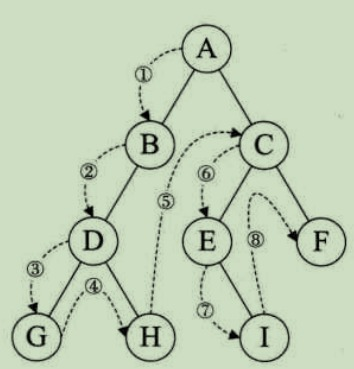
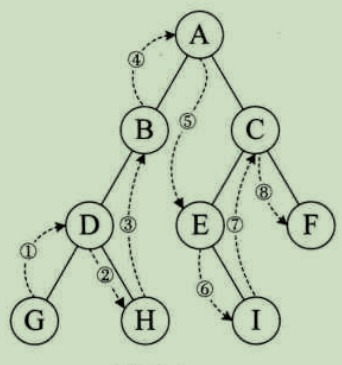
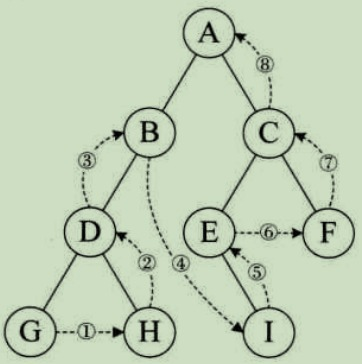
深度优先遍历（DFS）

• 前序遍历：根左右

• 中序遍历：左根右

• 后序遍历：左右根

广度优先遍历（层序遍历）

4.完全二叉树的操作

1.定义

typedef struct node{int no;struct node *pleftchild;struct node *prightchild;
}treenode;

2.使用形式（递归）

treenode *creat_treechild(int startno, int endno)
{treenode *ptmpnode = NULL;ptmpnode = malloc(sizeof(treenode));if(ptmpnode == NULL){perror("fail to malloc");return NULL;} ptmpnode->no = startno;ptmpnode->pleftchild = ptmpnode->prightchild = NULL;if(2*startno <= endno){ptmpnode->pleftchild = creat_treechild(2*startno, endno);}if(2*startno+1 <= endno){ptmpnode->prightchild = creat_treechild(2*startno+1, endno);}    return ptmpnode;
}/*前序遍历*/
int preorder_treechild(treenode *proot)
{printf("%d ",proot->no);if(proot->pleftchild != NULL){preorder_treechild(proot->pleftchild);}if(proot->prightchild != NULL){preorder_treechild(proot->prightchild);}return 0;
}/*中序遍历*/
int midorder_treechild(treenode *proot)
{if(proot->pleftchild != NULL){preorder_treechild(proot->pleftchild);}printf("%d ",proot->no);if(proot->prightchild != NULL){preorder_treechild(proot->prightchild);}return 0;
}/*后续遍历*/
int posorder_treechild(treenode *proot)
{if(proot->pleftchild != NULL){preorder_treechild(proot->pleftchild);}if(proot->prightchild != NULL){preorder_treechild(proot->prightchild);}printf("%d ",proot->no);return 0;
}int destroy_treechild(treenode *proot)
{if(proot->pleftchild){destroy_treechild(proot->pleftchild);}if(proot->prightchild){destroy_treechild(proot->prightchild);}free(proot);proot = NULL;return 0;
}

层序遍历

int layoutorder_treechild(treenode *proot)
{linkqueue *ptmpqueue = NULL;treenode *ptmpnode = NULL;ptmpqueue = creat_empty_linkqueue();enter_data_linkqueue(ptmpqueue, proot);while(!is_empty_linkqueue(ptmpqueue)){ptmpnode = out_data_linkqueue(ptmpqueue);printf("%d ", ptmpnode->no);if(ptmpnode->pleftchild != NULL){enter_data_linkqueue(ptmpqueue,ptmpnode->pleftchild);}if(ptmpnode->prightchild != NULL){enter_data_linkqueue(ptmpqueue, ptmpnode->prightchild);}}destroy_linkqueue(&ptmpqueue);return 0;
}