【第9话:感知算法基础1】深度学习神经网络模型基础知识概念入门简介
深度学习基础知识概念入门
深度学习是机器学习的一个分支,专注于使用多层神经网络来自动学习数据的特征表示。它通过模拟人脑的神经元结构,处理大规模数据,在图像识别、自然语言处理等领域有广泛应用。下面我将从基础概念开始,逐步解释深度学习的核心要素,确保内容结构清晰、易于理解。
1. 什么是深度学习?
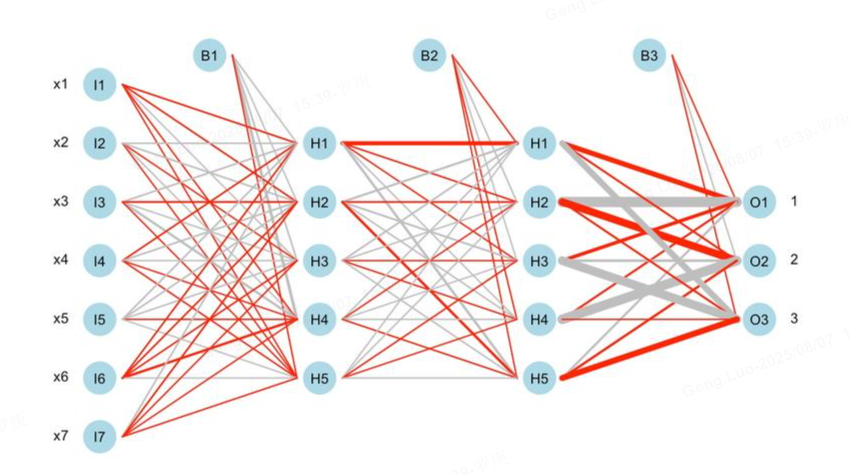
- 深度学习是一种基于人工神经网络的算法,能够从数据中自动提取高层次特征。与传统机器学习不同,它不需要手动设计特征,而是通过多层网络结构(称为“深度”)学习数据的复杂模式。
- 核心特点:使用多个隐藏层(hidden layers),每个层由多个神经元(neurons)组成,通过非线性变换逐步抽象数据。
2. 神经网络基础
神经网络是深度学习的核心架构,由多个相互连接的神经元组成。一个神经元模拟生物神经元,接收输入信号,计算加权和,再通过激活函数输出。
-
神经元模型:
- 输入:x=[x1,x2,…,xn]x = [x_1, x_2, \ldots, x_n]x=[x1,x2,…,xn](特征向量)。
- 权重:w=[w1,w2,…,wn]w = [w_1, w_2, \ldots, w_n]w=[w1,w2,…,wn](每个输入的重要性)。
- 偏置:bbb(调整输出偏移)。
- 加权和:z=w⋅x+b=∑i=1nwixi+bz = w \cdot x + b = \sum_{i=1}^{n} w_i x_i + bz=w⋅x+b=∑i=1nwixi+b。
- 激活函数:a=f(z)a = f(z)a=f(z),其中 fff 是非线性函数,引入模型的表达能力。
- 输出:aaa(激活值)。
-
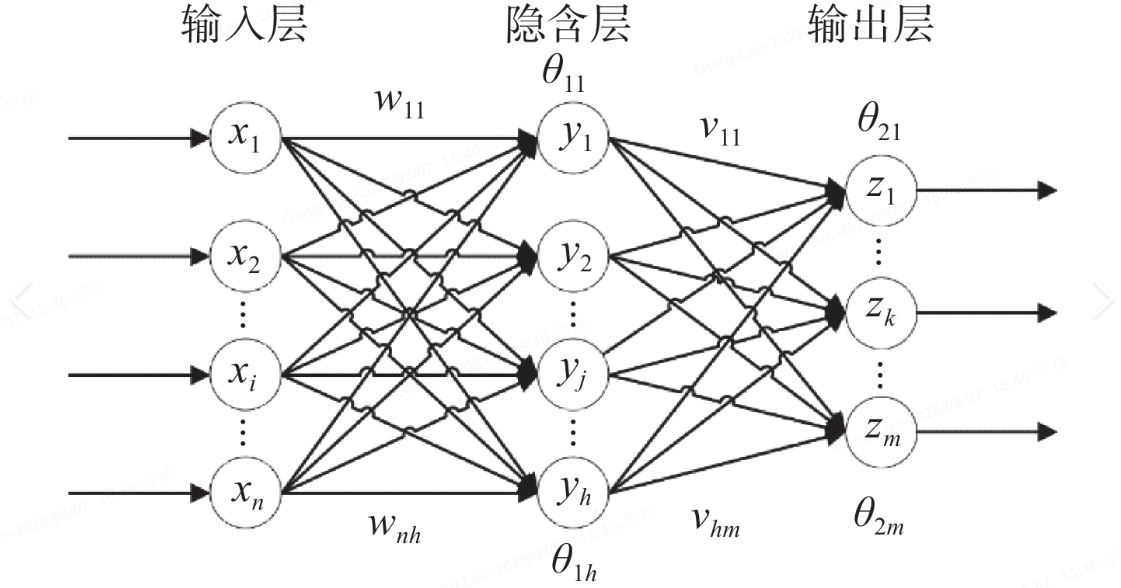
网络结构:
- 输入层:接收原始数据(如图像像素)。
- 隐藏层:多个中间层,每层有多个神经元,进行特征提取。
- 输出层:生成最终预测(如分类概率)。
- 例如,一个简单网络:输入层 → 隐藏层(ReLU激活) → 输出层(Sigmoid激活)。
3. 激活函数
激活函数引入非线性,使网络能拟合复杂关系。常见类型:
- Sigmoid:f(z)=11+e−zf(z) = \frac{1}{1 + e^{-z}}f(z)=1+e−z1,输出在0到1之间,适合二分类问题。
- ReLU(Rectified Linear Unit):f(z)=max(0,z)f(z) = \max(0, z)f(z)=max(0,z),计算高效,能缓解梯度消失问题。
- Tanh:f(z)=tanh(z)f(z) = \tanh(z)f(z)=tanh(z),输出在-1到1之间,类似Sigmoid但中心对称。
- 选择原则:ReLU常用于隐藏层,Sigmoid或Softmax用于输出层。
4. 前向传播(Forward Propagation)
前向传播是计算网络输出的过程:数据从输入层逐层传递到输出层。
- 步骤:
- 输入数据 xxx。
- 每层计算加权和 z(l)=W(l)a(l−1)+b(l)z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)}z(l)=W(l)a(l−1)+b(l),其中 W(l)W^{(l)}W(l) 是权重矩阵,a(l−1)a^{(l-1)}a(l−1) 是上一层输出。
- 应用激活函数 a(l)=f(z(l))a^{(l)} = f(z^{(l)})a(l)=f(z(l))。
- 最终输出 a(L)a^{(L)}a(L)(输出层结果)。
- 示例:对于一个单隐藏层网络:
a(1)=f(W(1)x+b(1)),y^=f(W(2)a(1)+b(2)) a^{(1)} = f(W^{(1)} x + b^{(1)}), \quad \hat{y} = f(W^{(2)} a^{(1)} + b^{(2)}) a(1)=f(W(1)x+b(1)),y^=f(W(2)a(1)+b(2))
其中 y^\hat{y}y^ 是预测值。
5. 损失函数(Loss Function)
损失函数衡量预测值 y^\hat{y}y^ 与真实值 yyy 的差距,指导网络优化。
- 常见类型:
- 均方误差(MSE):适合回归问题,L=1m∑i=1m(yi−y^i)2L = \frac{1}{m} \sum_{i=1}^{m} (y_i - \hat{y}_i)^2L=m1∑i=1m(yi−y^i)2,其中 mmm 是样本数。
- 交叉熵(Cross-Entropy):适合分类问题,L=−1m∑i=1m[yilog(y^i)+(1−yi)log(1−y^i)]L = -\frac{1}{m} \sum_{i=1}^{m} [y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)]L=−m1∑i=1m[yilog(y^i)+(1−yi)log(1−y^i)]。
- 目标:最小化损失函数 LLL,使预测更准确。
6. 反向传播(Backpropagation)和优化
反向传播通过计算梯度来更新网络权重,是训练的核心。
- 反向传播原理:
- 使用链式法则计算损失函数对每个权重的梯度 ∂L∂w\frac{\partial L}{\partial w}∂w∂L。
- 从输出层反向逐层传递误差。
- 梯度下降(Gradient Descent):
- 优化算法,通过迭代更新权重减小损失。
- 更新规则:wnew=wold−η∂L∂w w_{new} = w_{old} - \eta \frac{\partial L}{\partial w} wnew=wold−η∂w∂L,其中 η\etaη 是学习率(learning rate),控制步长。
- 变体:随机梯度下降(SGD)、Adam等,提高效率。
- 训练过程:
- 初始化权重(如随机小值)。
- 前向传播计算输出。
- 计算损失。
- 反向传播计算梯度。
- 更新权重。
- 重复直到收敛。
7. 常见网络类型
- 卷积神经网络(CNN):专为图像处理设计,使用卷积层提取局部特征(如边缘),池化层(pooling)降低维度。例如,用于图像分类。
- 循环神经网络(RNN):处理序列数据(如文本),通过隐藏状态记忆历史信息。变体包括LSTM(Long Short-Term Memory),解决长序列梯度消失问题。
- 其他:Transformer(用于自然语言处理)、自编码器(Autoencoder)用于降维。
8. 应用和总结
- 典型应用:图像识别(如人脸检测)、语音识别、机器翻译、推荐系统等。
- 关键优势:能自动学习特征,处理高维数据;但需大量数据和计算资源。
- 入门建议:从简单网络(如多层感知机)开始,使用框架如TensorFlow或PyTorch实践。深度学习是AI的核心技术,掌握这些基础概念后,可进一步探索高级主题如生成对抗网络(GAN)或强化学习。
通过以上步骤,您已了解深度学习的基本框架。实践中,建议通过小项目(如手写数字识别)加深理解。如果有具体问题,欢迎继续提问!
