深度学习-卷积神经网络CNN-1×1卷积层

1x1卷积核，又称为网中网（Network in Network）：NIN

卷积的本质是有效提取相邻像素间的相关特征，而1×1的卷积显然没有此作用。它失去了卷积层的特有能力——在高度和宽度维度上，识别相邻元素间相互作用的能力。

但是，它的唯一计算发生在通道上，具有融合不同通道的信息的能力。

• 例如：

  • 减少通道数（降维）：将输入特征图的通道数减少，从而降低计算复杂度。

  • 增加通道数（升维）：将输入特征图的通道数增加，从而提供更多的特征表示能力。

没有空间信息，相当于 ==> 把输入的二维信息拉成了一个一维向量信息。

其实这就更像是逐像素的共享权重，类似于全连接层。

相当于一个全连接层。

通常用于调整网络层的通道数量和控制模型复杂性。

多尺度特征融合：

• 在一些网络架构中，1×1卷积可以用来融合不同尺度的特征图。

• 例如，可以将不同大小的特征图转换为相同的通道数，然后进行融合，以便更好地利用多尺度信息。

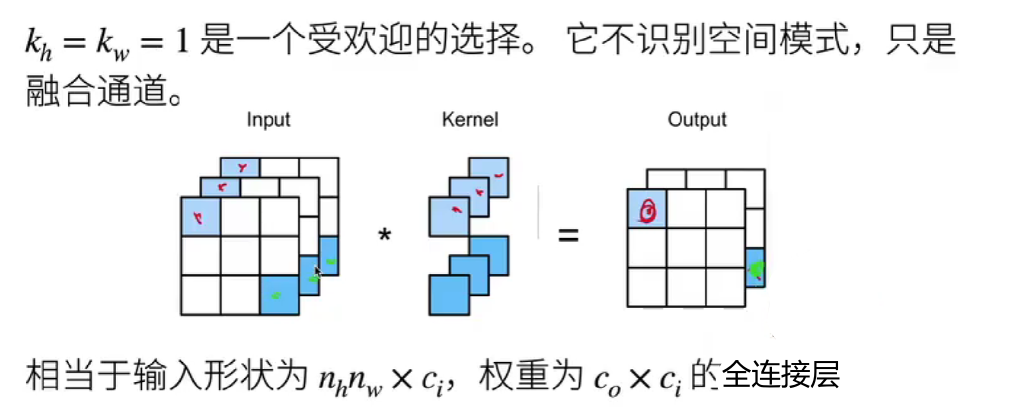
经典应用：

• 降维：在应用3×3或5×5卷积之前，使用1×1卷积减少输入通道数，从而降低计算量。

• 升维：将不同大小卷积核的输出转换为相同的通道数，以便进行特征融合。

• 增加非线性：1*1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep。

def corr2d_multi_in_out_1x1(X, K):c_i, h, w = X.shapec_o = K.shape[0]X = X.reshape((c_i, h * w))K = K.reshape((c_o, c_i))# 全连接层中的矩阵乘法Y = torch.matmul(K, X)return Y.reshape((c_o, h, w))X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6