论文Review BALM2 | 港大MARS出品!机器人顶刊TRO | 经典激光BA续作!BALM升级版 | TODO待精读
基本信息
题目:Efficient and Consistent Bundle Adjustment on Lidar Point Clouds
来源:IEEE TRANSACTIONS ON ROBOTICS 2023
学校:HKU-MARS
是否开源:https://github.com/hku-mars/BALM
摘要:激光BA,激光SLAM
同时确定传感器位姿和场景几何是机器人视觉的一个基本问题,通常通过光束平差( Bundle Adjustment,BA )来实现。本文提出了一种用于激光雷达的高效且一致的光束法平差方法。该方法使用边缘和平面特征来表示场景的几何特征,并直接最小化每个原始点到各自几何特征的自然欧氏距离。该公式的一个很好的特点是几何特征可以解析求解,极大地降低了数值优化的维度。为了更有效地表示和求解由此产生的优化问题,本文采用并形式化了point cluster的概念,即通过一组紧凑的参数——point cluster coordinates——对与同一特征相关的所有原始点进行编码。我们推导了基于点群坐标的BA优化的二阶闭式导数,并展示了它们的零空间和稀疏性等理论性质。基于这些理论结果,本文开发了一个高效的二阶BA求解器。除了估计激光雷达位姿外,该解算器还利用二阶信息来估计由测量噪声引起的位姿不确定性,从而得到激光雷达位姿的一致估计。此外,得益于点簇的使用,所开发的求解器从根本上避免了优化的所有步骤中每个原始点的枚举:成本cost,导数评估和不确定性评估。
Introduction
激光雷达已成为机器人实现高度自主的必不可少的传感技术。通过直接、密集、主动和精确( DDAA )的深度测量,激光雷达传感器具有构建稠密和准确的环境三维地图的能力。在实时和相对较低的计算成本。这些独特的优势使得激光雷达传感器对于各种需要实时、密集和精确的环境三维测绘的应用至关重要,例如自动驾驶,无人机导航和实时移动测绘。随着最近激光雷达技术的发展,这种趋势变得更加明显,这使得轻量级和高性能固态激光雷达的商业化和批量生产能够以显著更低的成本。(怎么说。。一些关于行业发展的非常好的废话)
许多基于激光雷达的技术,如基于激光雷达的里程计、同时定位与地图构建( SLAM )和多激光雷达校准,其中心任务是将激光雷达在不同姿态下测量的多个点云配准到一致的全局点云地图中。然而,主流的点云配准方法,如迭代最近点( ICP ) 及其变体( e.g. , generalized-ICP ),正态分布变换( NDT ) 和surfel配准[ 17 ],只允许两个点云的配准。这样的成对配准导致了里程计系统的增量扫描配准过程(例如. ,[ 17 ],[ loam ],[ fastlio2 ],LiTAMIN2 ),这将迅速积累漂移,或用于三维建图或多雷达标定的重复成对配准过程,这将带来巨大的计算成本。所有这些都需要一种高效的并发多扫描注册技术。
[17] J. Behley and C. Stachniss, “Efficient surfel-based SLAM using 3D laser range data in urban environments,” in Proc. Robot.: Sci. Syst., 2018.
同时进行多激光雷达扫描配准需要同时确定所有激光雷达姿态和场景几何形状,这一过程在计算机视觉中被称为光束平差( BA )。相比于视觉BA,它在摄影测量中已经很成熟,并在各种重要应用中发挥了基础作用,包括视觉里程计( VO ) ,视觉惯性里程计( VIO ) ,三维视觉重建和多相机标定,激光雷达BA具有类似的基础作用,但由于两大挑战,其成熟度较低。首先,激光雷达测量范围大,但扫描线间分辨率低。被测点云是稀疏的(有时甚至不重复)分布在一个大的三维空间中,使得在空间中扫描相同的点特征跨越不同的扫描变得困难(几乎不可能)。这从根本上阻止了使用直接的视觉光束法平差公式,这在很大程度上是基于点特征的,这得益于高分辨率图像准确地捕获了单个点特征。第二个挑战在于激光雷达传感器采集了大量的原始点(从数万点到百万点)。在激光雷达BA中处理所有这些点是非常计算密集型的。
在这项工作中,我们提出了一种专门针对激光雷达点云设计的高效且一致的BA框架。该框架沿用了我们之前的工作光束法激光雷达建图( BALM ),该框架基于激光雷达扫描中丰富的边缘和平面特征来描述激光雷达建图问题。BA公式自然地最小化扫描中每个点到相应边缘或平面的直接欧氏距离,而决策变量包括激光雷达姿态和特征(边缘与平面)参数。此外,还证明了几何参数(即,边缘和平面)可以解析求解,从而导致仅依赖于激光雷达姿态的优化。由于几何特征的数量往往较多,从优化中剔除这些几何特征会大幅降低优化维度。
我们提出的BA框架采用并形式化的一个关键概念是point cluster[ Eigen-factors ],[ 34 ],[ 35 ],它通过一组紧凑的参数,点簇坐标来总结与一个特征相关的激光雷达扫描的所有点。基于点簇,我们推导出BA优化及其决策变量(即,激光雷达姿态)的闭式导数(直到二阶)。我们证明了所提出的BA优化和闭式导数都可以用point cluster完全表示,而不需要枚举激光雷达扫描中的大量个体点。消除对个别原始点的依赖极大地加快了对成本函数和导数的评估,这进一步使我们能够开发一个高效和一致的二阶求解器BALM2.0。
[34] L. Zhou, D. Koppel, H. Ju, F. Steinbruecker, and M. Kaess, “An efficient planar bundle adjustment algorithm,” in Proc. IEEE Int. Symp. Mixed Augmented Reality, 2020, pp. 136–145.
[35] H. Huang et al., “On bundle adjustment for multiview point cloud registration,” IEEE Robot. Autom. Lett., vol. 6, no. 4, pp. 8269–8276, Oct. 2021.
Related Works
A. Multiview Registration
光束法平差问题类似于之前研究过的多视图配准问题。这些方法都采用了两层框架:第一层使用成对配准方法( 例如, ICP )来估计一组选定的扫描对的相对位姿。第二层从相对位姿出发,构建并求解位姿图,得到所有激光雷达姿态的最大后验估计。这样的两层框架将原始点配准与全局位姿估计解耦,使得每个原始点配准只涉及两次扫描(而不是所有扫描共享重叠)中包含的少量局部点,位姿图优化只涉及相对位姿(而不是原始点)中产生的少量约束。net 效应大大节省了时间,因此被大量用于在线激光雷达SLAM系统[ LIO-SAM ]。然而,在计算效率上的优势伴随着精度上的根本限制:成对扫描配准每次只考虑两个扫描之间的重叠,而重叠实际上是所有扫描共享的,应该同时进行配准。此外,位姿图优化只考虑相对位姿的约束,而原始点表示的映射一致性完全被忽略。因此,通常很难产生(甚至意识到)全局一致的地图,这对于高精度的定位和制图任务是必要的。
计算机视觉和计算机图形学的一些早期工作已经提出了多视图配准方法,直接从多幅图像中优化映射一致性,以实现三维物体的一致表面建模。早期的工作是ICP方法的直接推广,它最小化了一次扫描中一个已知的控制点到其余扫描中所有匹配的控制点之间的欧氏距离。在这个框架下,有的工作在优化中使用了四元数表示,还有工作将控制点之间的距离扩展到各自控制点周围的曲面之间的距离。最近的工作提出了一种两步配准方法:第一步使用K - means聚类从所有扫描中聚类点,第二步通过最小化簇中每个点到质心的欧氏距离来估计扫描位姿。由于这些方法依赖于扫描中的点特征,因此它们需要一个稠密的点云(例如,通过深度相机)来提取这些显著点特征。虽然这对于设计这些方法的小目标重建来说不是一个问题,但对于场景重建来说并非如此,正如上文所述,激光雷达测量值非常稀疏(有时甚至不重复)。
B. Bundle or Plane Adjustment
近年来,机器人学领域的研究人员对更正式地解决(激光雷达)点云的光束法平差问题表现出越来越大的兴趣。早期工作利用了光束法平差中的平面特征,并最小化扫描中测量的平面与由优化变量:扫描姿态和平面参数预测的平面之间的差异。这个公式后来被集成到一个基于关键帧的在线SLAM系统中[ 49 ]。由于该方法最小化了平面到平面的距离,因此需要对每次扫描进行分割,并预先估计包含的局部平面。这种平面分割和估计通常需要由RGB - D相机测量的密集点云,并在密集点云上展示工作。
[49] M. Hsiao, E. Westman, G. Zhang, and M. Kaess, “Keyframe-based dense planar slam,” in Proc. IEEE Int. Conf. Robot. Autom., 2017, pp. 5110–5117.
后来在[ 34 ]中提出了一种更正式的激光雷达点云光束平差方法,称为平面(光束)平差,它最小化扫描中每个点到由扫描姿态和平面参数(优化变量)预测的平面之间的自然欧氏距离。与过去工作中的平面到平面的距离相比,点到平面的度量更快,更准确,更适用于激光雷达传感器,因为稀疏的点云导致局部平面分割或估计的可靠性较低。此外,在点到平面度量中直接使用原始点也可以通过考虑原始点中的测量噪声来获得更加一致的优化变量估计。然后,采用Levenberg–Marquardt( LM )算法求解所建立的非线性最小二乘问题。为了减少与同一平面特征相关的大量点测量所带来的计算负担,[ 34 ]提出了一种reduction技术来消除残差和雅可比估计中个别点的枚举。此外,由于视觉光束法平差的结构非常相似,所提出的光束法平差还兼容Schur补技巧,在LM算法的每次迭代中消除了平面参数。这种平面调整方法在随后[ π-LSAM ],[ 52 ]或之前[ 53 ],[ 54 ]开发的许多在线激光雷达SLAM系统中大量使用。
[34] L. Zhou, D. Koppel, H. Ju, F. Steinbruecker, and M. Kaess, “An efficient planar bundle adjustment algorithm,” in Proc. IEEE Int. Symp. Mixed Augmented Reality, 2020, pp. 136–145.
[52] L. Zhou, D. Koppel, and M. Kaess, “LiDAR SLAM with plane adjustment for indoor environment,” IEEE Robot. Autom. Lett., vol. 6, no. 4, pp. 7073–7080, Oct. 2021.
[53] P. Geneva, K. Eckenhoff, Y. Yang, and G. Huang, “LIPS: LiDAR-inertial 3D plane SLAM,” in Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst., 2018, pp. 123–130.
[54] A. J. Trevor, J. G. Rogers, and H. I. Christensen, “Planar surface SLAM with 3D and 2D sensors,” in Proc. IEEE Int. Conf. Robot. Autom., 2012, pp. 3041–3048.
另一方面,Ferrer [ Eigen-factors ]利用类似于[ 34 ]的平面特征,最小化每个原始点对平面方程的任何偏差。由此得到的优化成本降低到协方差矩阵的最小特征值,因此称为Eigen-factors( EF )。作者进一步推导了cost function对lidar位姿和平面参数的闭式梯度,并采用基于梯度的方法迭代求解优化问题。由于特征值(如中所证实,见下文)的二阶性质,梯度法收敛非常缓慢(需要几百次迭代) [ Eigen-factors ],[ 52 ] .
我们的前期工作BALM又向更高效的光束法平差迈进了一步。类似于[ 34 ],BALM最小化扫描中每个点到平面(即,点到平面的度量)的自然欧氏距离。基于这个代价度量,BALM证明了所有的平面参数都可以预先用闭式解进行解析求解,从而可以将大量的平面参数从优化结果中完全移除。这种对平面参数的消去一般类似于研究较多的可分离最小二乘问题,但专门针对LiDAR BA问题而设计。特征消除的一个突出优点是优化维度的显著降低,这与之前所有的平面调整方法[ 34 ],[ 51 ],[ 52 ],[ 53 ]和视觉BA优化有着根本的区别。特征消除还去除了优化中平面表示带来的各种问题,如Hesse normal 表示( n , d) [ 34 ]中的法向约束问题,closest-point( CP )表示nd [ π-LSAM ],[ 52 ],[ 53 ]中的奇异性问题和四元数表示中的过参数化问题。通过特征消除,BALM进一步证明了点到平面(或边缘)的距离本质上是[ Eigen-factors ]中使用的协方差矩阵的特征值,从而统一了。这两个度量见[ Eigen-factors ]和[ 34 ] .虽然BALM和[ Eigen-factors ]都从BA优化中消除了特征,但[ Eigen-factors ]使用梯度方法来解决这个优化,这导致了如上所述的非常慢的收敛。相比之下,BALM推导了代价函数的二阶导数,并开发了类似于LM的二阶求解器。所开发的求解器需要明显较少的迭代次数才能收敛,当集成到激光雷达里程计和制图( LOAM )时可实现实时滑动窗口优化。与之前的方法[ Eigen-factors ]、[ 34 ]、[ 53 ]相比,BALM的另一个优势是整个框架除了平面特征外,还可以自然地扩展到边缘特征。
BALM的一个主要缺点是计算二阶导数包括Jacobian和Hessian需要枚举每个单独的激光雷达点,导致计算复杂度为,其中N是点的个数。因此,该方法很难应用于激光雷达点数量巨大的大规模问题中。这个问题在[ 35 ]中得到了部分解决,即在一个扫描局部帧中聚集与同一平面特征相关的所有点。然而,为了保证收敛,文献[ 35 ]通过增加一个额外的启发式惩罚项来修改代价函数,这并不是地图一致性的真实表示。此外,[ 35 ]中的代价函数仍然涉及类似于[ Eigen-factors ],[ 34 ],[ π-LSAM ],[ 52 ]和[ 53 ]的平面特征.为了减少优化大量特征参数所带来的计算量,该方法在优化过程中进一步修正了特征参数,从而降低了优化速度。
[35] H. Huang et al., “On bundle adjustment for multiview point cloud registration,” IEEE Robot. Autom. Lett., vol. 6, no. 4, pp. 8269–8276, Oct. 2021.
本文的BA公式基于BALM,因此继承了[ 34 ],[ π-LSAM],[ 52 ]和[ 53 ]的基本特征消除优势,以及相较于[ Eigen-factors ]的快速收敛优势。为了解决BALM中的计算复杂性,我们采用并形式化了point cluster的概念,这从根本上消除了代价函数、雅克比矩阵和Hessian矩阵计算中每个个体点的枚举。因此,计算复杂度与特征维数(类似于BALM )和点数(类似于和)均无关。我们的方法中的点簇类似于[ 35 ] (并且在和中也有应用)中使用的点聚合,但整体的BA公式根本不同:1 )它最小化真实地图一致性(点到平面的距离),而不需要与任何其他启发式惩罚进行权衡;2 )它执行精确的特征消除,具有严格的证明,而不是经验性的固定。
III. BUNDLE ADJUSTMENT FORMULATION AND OPTIMIZATION
A. BA Formulation
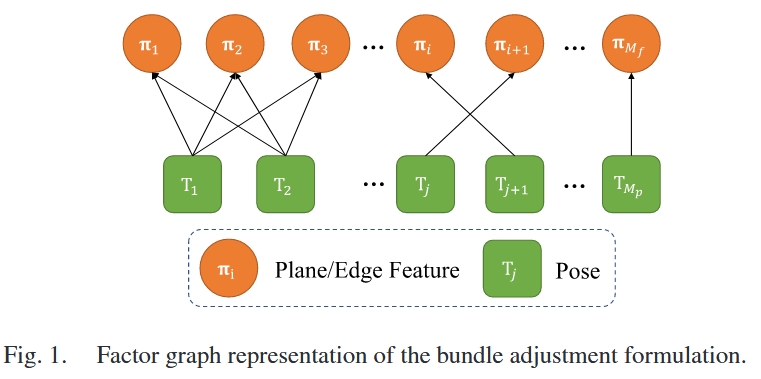


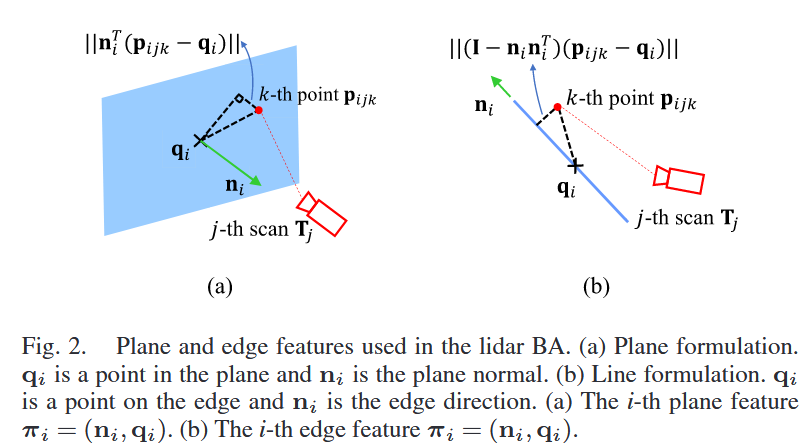
(这里主要介绍了激光BA的构成,包含面特征和线特征)
B. Elimination of Feature Parameters


C. Point Cluster
优化(9)中,计算 Ai 需要枚举所有点,计算昂贵。引入点簇避免枚举:点簇是有限点集的紧凑表示,支持刚体变换和合并操作。
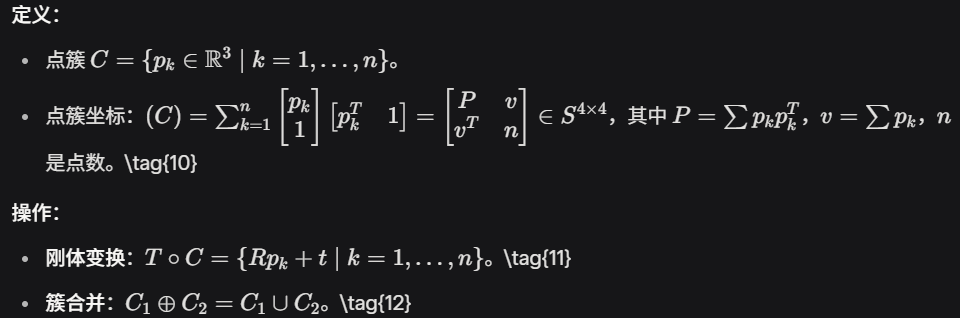

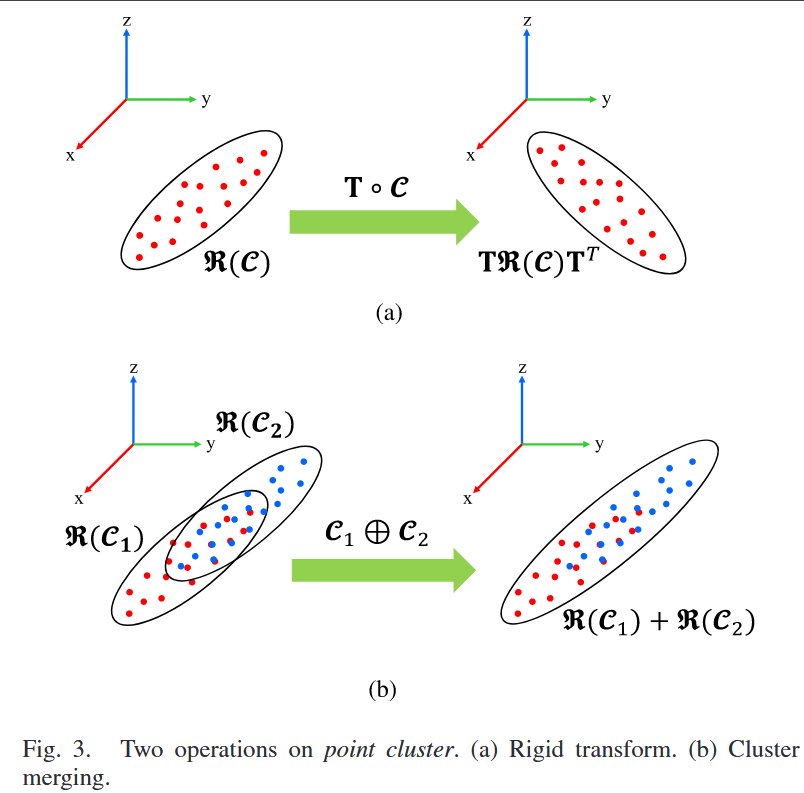


D. First- and Second-Order Derivatives


E. Second-Order Solver

F. Covariance Estimation

(看懵逼了,这不是短时间能看完的,这篇论文的公式推导没有一周的时间能消化完吗)
TODO,开个坑之后有时间再精读吧……
实验
硬件平台
数据集
Benchmark
初体验
TODO
