当前位置：首页 > news >正文

代数——第6章——对称性(Michael Artin)

news 2025/8/7 7:18:37

第6章对称性(Symmetry)

6.1 平面图形的对称性(Symmetry of plane figures)

6.2 等距性(Isometries)

6.3 平面的等距(Isometries of the plane)

6.4 平面上正交算子之有限群(Finite groups of orthogonal operators on the plane)

6.5 离散等距群(Discrete groups of isometries)

6.6 平面晶体群(Plane crystallographic groups)

6.7 抽象对称性：群运算(Abstract symmetry:group operations)

6.8 陪集上的运算(The operation on cosets)

6.9 计数公式(The Counting formula)

6.10 基于子集的运算(Operations on subsets)

6.11 置换表示(Permutation presentations)

6.12 旋转群之有限子群(Finite subgroups of the rotation groups)

L'afgébre n'est qu'une géométrie écrite; la géométrie n'est qu'une algébre figurée.

(Algebra is but written geometry and geometry is but figured algebra)

(代数只不过是符号化的几何；而几何也不过是图形化的代数。)

---------------------------------------------------Sophie Germain

对称性提供了群的一些最具吸引力的应用。群的发明是为了分析某些代数结构——域扩展(第16章)——的对称性。由于对称性是一种常见现象，它是群论应用的两种主要方式之一。另一种是通过群表示，这将在第10章讨论。我们在第一节中学习的平面图形的对称性，将为第6.7节介绍的群运算的一般概念提供丰富的示例和背景。

我们允许自由运用几何推理。如何将论证带回到几何公理，留待下次再讨论。

6.1 平面图形的对称性(Symmetry of plane figures)

(6.1.1) 双侧对称性(Bilateral Symmetry)

(6.1.2) 旋转对称性(Rotational Symmetry)

(译注：旋转对称图形是指绕平面内某定点旋转特定角度后与原图形重合的平面图形，该定点称为旋转中心，最小重合角度称为旋转角。)

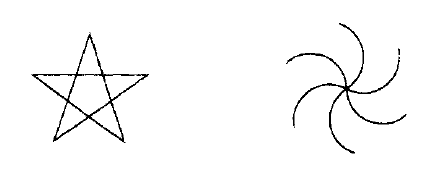
(6.1.3) 平移对称性(Translational Symmetry)

像这样的图形应该在两个方向上无限延伸。此外，还有第四种对称性，尽管它的名字——滑移对称——可能不太为人熟知：

(6.1.4) 滑移对称性(Slide Symmetry)

如下图所示的墙纸图案，可能具有两个独立的平移对称性，

(6.1.5)

还可能出现其他对称性复合。星形既有双侧对称性，也有旋转对称性。下图中，平移对称性和旋转对称性结合在一起：

(6.1.6)

另外一个例子

(6.1.7)

平面的刚体运动(a rigid motion)称为等距运动(isometry)(译注：或称为全等，或全等变换，因为这种运算保持平面上物体中点之间的距离不变)，如果一个等距运动将平面的一个子集 F 移到其自身，则称其为 F 的一个对称。F 的所有对称性集合构成了平面所有等距运动群的一个子群：如果 m 和 $m^{'}$ 将 F 带至 F，那么复合映射 $mm^{'}$ 也同样如此，等等。这就是 F 的对称群。

图 6.1.3 具有无限循环对称群，它们由平移 t 生成，平移 t 将图形向左移动一个单位。即

$G = \{..., t^{-2} ,t^{-1} ,1 , t , t^{2} , ... \}$ 。

图 6.1.7 还具有平移对称性以外的其它对称性。

6.2 等距性(Isometries)

(译注：isometry 在以下表述中视语境译可能译为“等距，等距性，等距同构，等距映射，等距变换”，在本质上都是等价的。)

$\mathbb{R}^{n}$ 的点之间的距离是向量 u – v 的长度 |u – v | 。n 维空间 $\mathbb{R}^{n}$ 的一个等距映射是一个从 $\mathbb{R}^{n}$ 到其自身的保距映射 f ，即是这样一个映射：对于 $\mathbb{R}^{n}$ 中的所有 u 和 v ，其使得：

(6.2.1) $| f (u) - f (v) | = | u - v |$ 。

一个等距映射会将一个图形映射到一个全等图形。

例子 6.2.2:

(a) 正交线性算子是一个等距映射。

因为一个正交算子 φ 是线性的，即 φ (u) – φ (v) = φ (u – v) ，因此 | φ (u ) – φ (v) | = |φ ( u – v ) | , 且因为 φ 是正交的，其保留点积从而保留长度。因此 |φ ( u – v )| = | u – v | 。

(b) (将一个向量)平移一个向量 a 的平移 $t_{a}$ 是一个等距映射，即由 $t_{a}(x)=x+a$ 定义的映射。

平移不是线性算子，因为它不会将 0 映射到 0 ，当然除开 0 向量的平移，因为它是恒等映射。

定理 6.2.3 下面基于映射 $\varphi : \mathbb{R}^{n} \longrightarrow \mathbb{R}^{n}$ 的条件是等价的：

(a) φ 是一个固定了原点的等距映射： φ(0) = 0 ，

(b) φ 保留点积：(φ(v)• φ(w)) = (v• w) (对于所有的 v 和 w )，

我们已经知道 (c) 蕴涵 (a)。我们接下来要展示的蕴涵 (b) ⟹ (c) 的简洁证明，是由 Sharon Hollander 几年前在麻省理工学院(MIT)代数课上发现的。

引理 6.2.4 令 x 和 y 为 $\mathbb{R}^{n}$ 中的点，若这三个点积 (x • x), (x • y) , 和 (y • y) 是相等的，则 x = y 。

证明：

假设 (x • x) = (x • y) = (y • y) 。则

( (x - y) • (x - y) ) = (x • x) - 2(x • y) + (y • y) = 0 。

(x - y) 的长度是零，从而 x = y 。

定理 6.2.3 之证明：(b) ⟹ (c)：

令 φ 为一个保留点积的映射。则只要其是一个线性算子 (5.1.12)，那么其将是正交的。为了证明 φ 是一个线性算子，我们必证明对于所有的 u 和 v ，以及所有的标量 c ，有 φ (u + v) = φ (u) + φ (v) 以及 φ (cv) = cφ (v) 。

已知 $\mathbb{R}^{n}$ 中的 x ，我们将用符号 $x^{'}$ 来表示 φ (x) 。此外，我们引入符号 w 来表示和，表示为 w = u + v 。则将证明的关系 φ (u + v) = φ (u) + φ (v) 成了 $w^{'}=u^{'}+v^{'}$ 。

我们将 $x=w^{'}$ 和 $y=u^{'}+v^{'}$ 代入引理 6.2.4 。为了证明 $w^{'}=u^{'}+v^{'}$ ，只需证明这3个点积

$(w^{'} \cdot w^{'})$ ， $(w^{' }\cdot (u^{'} + v^{'}))$ ，和 $((u^{'} + v^{'}) \cdot (u^{'} + v^{'}))$

相等即可。我们将第二个和第三个点积展开。只需证明

$(w^{'} {\cdot} w^{'}) = (w^{'} {\cdot} u^{'}) + (w^{'} {\cdot} v^{'}) = (u^{'} {\cdot} v^{'}) + 2(u^{'} {\cdot} v^{'}) + (v^{'} {\cdot}v^{'})$

即可。根据假设，φ 保留了点积。因此，我们可以删去素数： $(w^{'} {\cdot} w^{'}) = (w {\cdot} w)$ ，等等。则只需证明

(6.2.5) $(w{\cdot}w) = (w {\cdot} u) + (w {\cdot} v) = (u {\cdot} u) + 2(u {\cdot} v) + (v {\cdot} v)$

即可。

然而，现在需要证明 $w^{'} = u^{'} + v^{'}$ ，根据定义 w = u + v 是成立的。因此，现在我们可以用 u + v 替代 w 。则 (6.2.5) 成立。

为了证明 φ(cv) = cφ(v) ，我们记 u = cv ，且必须证明 $u^{' }= cv^{'}$ 。这个证明与我们刚才已经给出的证明类似。

定理 6.2.3 之证明：(a) ⟹ (b)：

令 φ 为一个固定了原点的等距映射。按照素数记法，φ 的保距属性解读为：对于 $\mathbb{R}^{n}$ 中的所有 u 和 v ，有

(6.2.6) $((u^{'} + v^{'}){\cdot}(u^{'} + v^{'})) = ((u - v) {\cdot} ( u - v))$ 。

我们代入 v = 0 。由于 $0^{'} = 0$ ，所以 $(u^{'} {\cdot} u^{'}) = (u {\cdot} u)$ 。类似地，有 $(v^{'} {\cdot} v^{'}) = (v {\cdot} v)$ 现在，当我们展开 (6.2.6) 从等式的两端抵消掉 (u • u) 和 (v • v) 即可导出 (b) 。

推论 6.2.7 $\mathbb{R}^{n}$ 的每一个等距映射 f 都是一个正交线性算子和一个平移的复合。更确切地说，若 f 是一个等距映射且若 f (0) = a ,则 $f = t_{a}(\varphi) ,$ 其中， $t_{a}$ 是一个平移，而 φ 是一个正交线性算子。则 f 的这个表达是唯一的。

证明：

令 f 为一个等距映射，令 a = f (0) ，并令 $\varphi = t_{-a}f$ 。则 $t_{-a}\varphi = f$ 。此推论相当于断言 φ 是一个正交线性算子。由于 φ 是等距变换 $t_{-a}$ 和 f 的复合，因此它是一个等距变换。此外， $\varphi (0) = t_{-a} f (0) = t_{-a} f (a) = 0$ , 则 $\varphi = t_{-a}f$ 。

为了使用等距的表达式 $t_{-a}\varphi$ ，我们必须确定两个这样的表达式之积(复合)。我们知道，正交算子的复合 φψ 也是一个正交线性算子。其它的法则有：

(6.2.8) $t_{a} t_{b} = t_{a+b}$ 和 ${\varphi}t_{a} = t_{a^{'}}{\varphi} ( a^{'} = {\varphi}(a))$ 。

我们验证最后一个关系：

${\varphi}t_{a} (x) = {\varphi}(x + a) = {\varphi}(x) + {\varphi}(a) = {\varphi}(x) + a^{'} = t_(a^{'} ){\varphi}(x)$ 。

推论 6.2.9 $\mathbb{R}^{n}$ 的所有等距之集合构成一个群，我们用 $M_{n}$ 表示该群，并以函数复合作为复合定律。

证明：

等距的复合也是一个等距，而一个等距之逆也是一个等距映射，因为正交算子和平移是可逆的，且若 $t_{a}\varphi$ ，则 ${\varphi}^{-1} t_{a}^{-1} = {\varphi}^{-1} t_{-a}$ 。这是等距的一个复合。

注意：不难(直接根据定义)验证等距的可逆性。

同态(homomorphism) $M_{n} \longrightarrow O_{n}$

存在一个重要的映射 $\pi:M_{n} \longrightarrow O_{n}$ ，其通过删除掉一个等距 f 的平移部分而定义。我们(唯一地)记 f 为形式 $f = t_{a}\varphi$ ，且定义 π ( f ) = φ 。

命题 6.2.10 映射 π 是一个满射同态。其核是一个平移集合 $T=\{t_{v}\}$ , 这是 $M_{n}$ 的一个正规子群。

证明：

很明显 π 是满射的，一旦我们证明了 π 是一个同态，则很显然 T 是其核，因此，T 是一个正规子群。我们必须证明，若 f 和 g 是等距，则 π ( fg ) = π ( f ) π ( g ) 。不妨设 $f = t_{a}\varphi$ 和 $g = t_{b}\psi$ ，使得 π ( f ) = φ 和 π ( g ) = ψ 。则 ${\varphi}t_{b} = t_{b^{'}}{\varphi}$ ，其中， $b^{' }= \varphi( b )$ 和 $fg = t_{a}{\varphi}t_{b}{\psi} = t_{a+b^{'}}{\varphi}{\psi}$ 。因此，π ( fg ) = φψ = π ( f ) π ( g ) 。

坐标变换(Change of Coordinates)

令 P 为一个 n 维空间。等距变换的公式 $t_{a}\varphi$ 取决于我们选择的坐标系，因此，我们来算一下，当坐标系改变时公式会如何变化。我们允许通过正交矩阵进行变换，也允许通过平移原点进行变换。换言之，我们可以通过任何等距变换来改变坐标系。

为了分析坐标变换对等距的影响，我们首先在不考虑坐标的情况下考虑一个等距 f ，P 的一个点 p , 及其像 q = f (p)。当我们引入坐标系统的时候，空间 P 就与 $\mathbb{R}^{n}$ 关联起来了，点 p 和 q 具有坐标，不妨设 $x = (x_{1},...,x_{n})^{t}$ ， $y= (y_{1},...,y_{n})^{t}$ 。此外，等距 f 将有一个根据坐标的公式 $t_{a}\varphi$ ；我们称这个公式为m 。公式 q = f (p) 转化为 $y=m(x)(=t_{a}\varphi(x))$ 。我们想确定，当坐标变换时，坐标向量和公式会发生什么变化。线性算子中基变换的类似计算给出了线索：m 会通过共轭变换而改变。

我们的坐标变换将由一些等距给出，我们用 η (eta)表示。并令 p 和q的新坐标向量分别为 $x^{'}$ 和 $y^{'}$ 。f 的新坐标公式 $m^{'}$ 使得 $m^{'}(x^{'}) = y^{' }$ 。此外，我们还有公式 $\eta(x^{'}) = x$ , 其类似于基变换公式 $PX^{'} = X$ (3.5.11) 。

我们将 $\eta(x^{'}) = x$ 和 $\eta(y^{'}) = y$ 代入公式 m (x) = y , 得到 $m{\eta}(x^{'}) = {\eta}(y^{'})$ , 或 ${\eta}^{-1} m{\eta}(x^{'}) = y^{'}$ 。新公式是共轭的，如预期：

(6.2.11) $m^{' }= {\eta } ^{-1}m{\eta }$ 。

推论 6.2.12 同态 $\pi:M_{n} \longrightarrow O_{n}$ (6.2.10) 当原点通过平移而变换时其保持不变。

当原点通过平移 $t_{v} = \eta$ 而变化时，(6.2.11) 解读为 $m^{'} = t_{-v} mt_{v}$ 。由于平移位于 π 的核中且由于 π 是一个同态，因此 $\pi(m^{'}) = \pi(m)$ 。

定向(Orientation)

$\mathbb{R}^{n}$ 上的一个一个正交算子的行列式是 ±1 。若其行列式为 1 ，则称此正交算子为保向算子(orientation-preserving),若其行列式是 -1 ，则称此正交算子是逆向算子(orientation-reversing)。类似地，对于一个等距映射 f ，当其记为形式 $f=t_{a}\varphi$ 时，称其为保向等距(或逆向等距)。

如果平面的等距映射(或变换)将平面的正面和反面互换，则为逆向等距映射；如果平面的等距映射将正面映射到正面，则为保向等距映射。

映射

(6.2.13) $\sigma : M_{n} \longrightarrow \{ \pm{1}\}$

是一个如同态，其将一个保向等距映到 1 ，将一逆向等距映射到 –1 。

6.3 平面的等距(Isometries of the plane)

在本节中，我们从代数和几何两个角度来描述平面的等距性。

我们将平面的等距同构群表示为 M。为了计算该群，我们选择一些特殊的等距同构作为生成元，并求得它们之间的关系。这些关系与定义对称群 $S_{3}$ 的关系有些类似，但由于 M 是无限的，因此它们的数量更多。

我们选择一个坐标系统，并用它将平面 P 和空间 $\mathbb{R}^{2}$ 关联起来。然后我们选择平移、围线原点的旋转、以及围绕 $e_{1}$ 轴的反射作为生成元(译注：通过反射形成的像，即镜像，就像镜子通过反射形成的虚像，像在对称线的另一侧，故称其为反射)。我们用 $\rho_{\theta}$ 来表示扫过角度 θ的旋转，用 r 来表示围绕 $e_{1}$ 轴的反射，这二者都是线性算子，其矩阵 R 和 $S_{0}$ 如前所示(见(5.1.17)和(5.1.16))。

(6.3.1)

(1) 平移一个向量 a 的平移 $t_{a}$ : $t_{a}(x)=x+a=\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix} + \begin{bmatrix} a_{1}\\a_{2} \end{bmatrix}$ 。

(2) 围绕原点扫过角度 θ 的旋转 $\rho_{\theta}$ ： $\rho_{\theta}(x)=\begin{bmatrix} \cos{\theta}&-\sin{\theta}\\ \sin{\theta}&\cos{\theta} \end{bmatrix}\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}$ 。

(3) 围绕 $e_{1}$ 轴的反射： $r(x)=\begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix}\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix}$ 。

我们没有列出所有的等距。围绕原点以外的点的旋转不包括在内，围绕其他线或滑移的反射也不在内。然而，M 的每一个元素都是这些等距之积，因此它们生成了群。

定理 6.3.2 令 m 为平面的一个等距，则对于一个唯一地确定的向量 v 和一个角度和 θ ，有 $m = t_{v} \rho_{\theta}$ 或 $m = t_{v}{\rho}_{\theta}r$ 。

证明：

推论 6.2.7 断言，任意一个等距都可以唯一地记为形式 $m = t_{v}{\varphi}$ (其中 φ 是一个正交算子)。 $\mathbb{R}^{2}$ 上的正交线性算子是围绕原点的旋转 $\rho_{\theta}$ ，且是围绕直线的通过原点的反射。反射具有形式 $\rho_{\theta}r$ (见 5.1.17 )。

一个形如 $t_{v} \rho_{\theta}$ 的等距当 $t_{v}{\rho}_{\theta}r$ 逆转方向时其保持方向。可以使用公式 (6.3.1)(另见(6.2.8)) 验证这个法则。

(6.3.3)

$\rho_{\theta} t_{v}= t_{v^{'}} \rho_{\theta}$ ( 其中， $v^{'} = {\rho}_{\theta}(v)$ ) ，

$rt_{v} = t_{v^{'}} r$ ( 其中， $v^{' }= r(v)$ ) ，

$r{\rho}_{\theta} = {\rho}_{-\theta}r$ 。

$t_{v} t_{w} = t_{v+w}$ , ${\rho}_{\theta} {\rho}_{\eta} = {\rho}_{{\theta}+{\eta}}$ 且 rr = 1 。

下面的定理从几何上描述了平面的等距。

定理 6.3.4 平面的每一个等距都具有下列之一的形式：

(a) 保向等距：

(i) 平移：一个发送 p ⇝ p + v 的映射 $t_{v}$ 。

(ii) 旋转：平面围绕某个点扫过一个非零角度 θ 的旋转。

(b) 逆向等距：

(i) 反射：围绕(或围绕)一条直线 𝓁 呈双侧对称性。

(ii) 滑动反射(glide reflection)(简称滑射(glide))：围绕(或围绕)一条直线 𝓁 的反射，根据按平行于一条直线 𝓁 平移一个非零向量而推导。

这个著名定理的证明如下。其推论之一是，围绕两个不同点的旋转的复合(或复合)，相当于围绕第三个点的旋转，除非它是平移。这并不显而易见，但从定理可知，因为复合是保向的。

某些复合更容易可视化。绕同一点扫过角度α 和β 旋转之复合，就是绕该点扫过角度 α + β 的旋转。按向量 a 和 b 的平移之复合就是按其和 a + b 的平移。

围绕非平行直线 ${\ell}_{1}$ , ${\ell}_{2}$ 的反射之复合就是一个围绕交叉点 $p={\ell}_{1}\cap{\ell}_{2}$ 的旋转。这一点也可以根据定理推导，因为复合是保向的，其固定了点 p 。围绕平行线的反射之复合是一个按与直线正交的向量之平移。

定理 6.3.4之证明：

首先我们考虑保向等距。令 f 为一个非平移保向等距。我们必须证明 f 是一个围绕同一点的旋转。我们选择一个坐标系，将 f 的公式按(6.3.3)中的公式那样记为 $m=t_{a}\rho_{\theta}$ 。

由于m 非平衡，所以 θ ≠ 0 。

引理 6.3.5 形如 $m=t_{a}\rho_{\theta}$ (θ ≠ 0) 的一个等距映射 f 是一个绕平面上的一个点扫过角度 θ 的旋转。

证明：

为了简化记法，我们用 ρ 表示 $\rho_{\theta}$ 。为了证明 f 是一个围绕同一个点 p 扫过角 θ 的旋转，我们通过平移 $t_{p}$ 作坐标变换。我们希望通过选择一点 p 使得等距映射 f 的新

公式为 $m^{'} = \rho$ 若如此，则 f 将是一个围绕点 p 且扫过角度 θ 的旋转。

这个坐标变换的法则是 $t_{p}(x^{'}) = x$ , 从而， f 的新公式为 $m^{'} = t_p^{-1} mt_{p} = t_{-p} t_{a} {\rho}t_{p}$ (6.2.11) 。我们利用法则(6.3.3): ${\rho}t_{p} = t_{p^{'}} {\rho} \; ( {\rho}^{'} = {\rho}(p) )$ 。则若 $b = -p + a + p^{'} = a + \rho(p) - p$ ，我们将有 $m^{'} = t_{b}\rho$ 。我们希望选择一个 p 使得 b = 0 。

令 I 表示恒等算子，并令 c = cos(θ) 且 s = sin(θ)。则线性算子 I – ρ 的矩阵为

(6.3.6) $\begin{bmatrix} 1-c&s \\ -s&1-c \end{bmatrix}$ 。

其行列式是 2 – 2c = 2 – 2cos(θ) 。除非 cos(θ) = 1 ,否则行列式不等于0 ，仅当 θ = 0 时才会发生这种情况。由于 sin(θ) ≠ 0 ，故 p 的方程 (1 - ρ) p = a 具有唯一解。当需要时，可以显式地求解这个方程。

点 p 是等距 $t_{a}\rho_{\theta}$ 的定点，可以按几何方法求得，如下图所示。经过原点的直线 𝓁 垂直于向量 a 。夹角为 θ 的扇形如此放置是为了便于用 𝓁 进行平分，定点 p 通过将向量 a插入扇形而确定，如下图所示。

(6.3.7)

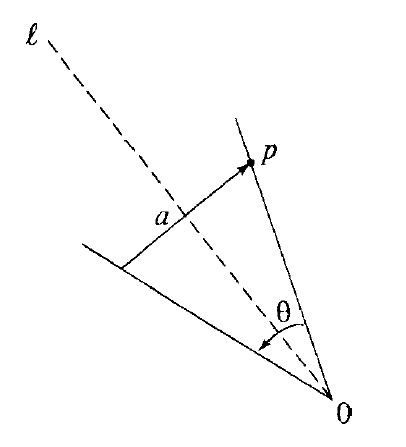
----------------------------------------等距 $t_{a}\rho_{\theta}$ 的定点--------------------------------

为了完成定理 6.3.4 的证明，我们证明一个逆向等距 $m=t_{a}\rho_{\theta}r$ 是一个滑动或一个反射。为此，我们变更坐标。等距 $\rho_{\theta}r$ 是一个围绕一条经过原点的直线 $\ell_{0}$ 的反射。我们也可以旋转坐标使得 $\ell_{0}$ 成为水平轴。在新坐标系统中，反射成了我们的标准反射 r ，而平移 $t_{a}$ 仍旧是一个平移，尽管向量 a 的坐标已经改变。我们任用符号 a来表示这个新的向量。在新坐标系统中，等距成了 $t_{a}r$ 。其表现为

$m\begin{bmatrix} x_{1}\\x_{2} \end{bmatrix} =t_{a}\begin{bmatrix} x_{1}\\-x_{2} \end{bmatrix} = \begin{bmatrix} x_{1}+a_{1}\\-x_{2}+a_{2} \end{bmatrix}$ 。

这个等距是通过围绕直线 $\ell :\{ x_{2} = \frac{1}{2} a_{2} \}$ 的反射而获得的滑射，可通过按向量 $a_{1}e_{1}$ 的平移而推导。若 $a_{1}=0$ ，则 m 是一个反射。

这样就完成了证理 6.3.4 的证明。

推论 6.3.8 等距 $t_{a}\rho_{\theta}r$ 的滑射直线平行于反射 $\rho_{\theta}r$ 的直线。

固定原点的等距是正交线性算子，因此，当坐标选定后，正交群 $O_{2}$ 就成了等距群 M 的一个子群。我们也可以考虑固定平面上原点以外的点的等距群 M 的子群。该群与正交群的关系将在下一个命题中给出。

命题 6.3.9 假设平面中的坐标已选定，使得正交群 $O_{2}$ 成了固定了原点的等距群 M 之一个子群。则平面的定点 p 的等距之群是共轭子群 $t_{p} O_{2} t_{p}^{-1}$ 。

证明：

若一个等距 m 固定了点 p ，则 $t_{p}^{-1} mt_{p}$ 固定了原点。 $t_{p}^{-1} mt_{p}o = t_{p}^{-1} m p = t_{p}^{-1}p = o$ 。反之，若 m 固定 o ，则 $t_{p}mt_{p}^{-1}$ 固定 p 。

我们可以按这种方式可视化围绕一个点 p 的旋转：首先，按 $t_{-p}$ 将 p 点移至原点，然后围绕原点旋转，完成后再平移 p 回点。

现在回到 (6.2.10) 中定义的同态 $\pi: M \longrightarrow O_{n}$ 。上述的讨论表明：

命题 6.3.10：令 p 为平面中的一点，并令 ${\rho}_{\theta,p}$ 表示围绕 p 点扫过 θ 角的旋转。则 ${\pi}({\rho}_{\theta,p})=\rho_{\theta}$ 。类似地，若 $r_{\ell}$ 是一个围绕一条直线 𝓁 的旋转或一个围绕平行于 x 轴的滑射直线 𝓁 的滑射，则 ${\pi}(r_{\ell})=r$ 。

点和向量(Points and Vectors)

在本书的大部分内容中，都没有令人信服的理由来区分平面 $P=\mathbb{R}^{2}$ 上的某一点 p 和从原点 0 到某一点 p 的向量(在微积分书籍中通常记为 $\overrightarrow{op}$ )。然而，在处理等距时，最好保持这种区别。因此，我们引入平面的另一个副本，我们称之为 V，并将其元素视为

平移向量。按V 中的一个向量v 的平移作用于 P 上的某一点 p ，记为 $t_{v}(p)=p+v$ 它将平面上的每一个点平移 v 。V 和 P 均为平面。仅当我们作做标变换的时候，它们的差异才变得明显。假设我们通过平移 $\eta=t_{w}$ 来移动坐标。变换坐标的法则为 $\eta(p^{'}) = p$ 或 $p^{'} + w = p$ 。同时，一个等距变化为 $m^{'} = {\eta}^{-1}m{\eta} = t_{-w}mt_{w}$ (6.2.11) 。如果我们带着 $m=t_{v}$ 应用这个法则，则 $m^{'} = t_{-w} t_{v} t_{w} = t_{v}$ 。P 的点获得了新的坐标，但平移向量不变。

在另一方面，若我们通过正交算子 φ 改变坐标，则 $\varphi(p^{'}) = p$ , 且若 $m = t_{v}$ ，则 $m^{'} = {\varphi }^{-1} t_{v}\varphi$ ，其中 $v^{'} = {\varphi}^{-1} v$ 。因此， ${\varphi}v^{'} = v$ 。通过正交算子执行的坐标变换的影响在P 上与在 V 上是一样的。

基于P 和V的坐标变换的唯一区别在于，在 P 中原点不必固定，而在 P 中，以零向量作为原点。

正交算子作用于 P ，但其不作用于 V ，除非其选定了原点。

6.4 平面上正交算子之有限群(Finite groups of orthogonal operators on the plane)

定理 6.4.1 令 G 为正交群 $O_{2}$ 的一个有限子群。则存在一个整数 n ，使其成为下列群之一：

(a) $C_{n}$ : 由旋转 $\rho_{\theta}$ (θ = 2π/n ) 生成的 n 阶循环群(cyclic group)。

(b) $D_{n}$ : 由后述两个元素生成的 2n 阶二面体群(dihedral group)，即，旋转 $\rho_{\theta}$ (θ = 2π/n) 和围绕一条经过原点的直线 𝓁 的反射 $r^{'}$ 。

在证明此定理之前，我们将简要介绍一下二面体群 $D_{n}$ 。此群依赖于反射线，但若我们选择一个坐标系统使得 𝓁 成为水平轴，则此群将包含我们的标准反射 r , 标准反射的矩阵为

(6.4.2) $\begin{bmatrix} 1&\\ &-1 \end{bmatrix}$ 。

则若我们同样记 $\rho_{\theta}$ 为 ρ ，则此群的 2n 个元素将是 ρ 的 n 个幂 $\rho^{i}$ 和 n 个积 $\rho^{i}r$ 。交换 ρ 和 r 的法则为

$r\rho=\begin{bmatrix} 1&\\ &-1 \end{bmatrix}\begin{bmatrix} c&-s\\ s&c \end{bmatrix}=\begin{bmatrix} c&s\\-s&c \end{bmatrix}\begin{bmatrix} 1&\\ &-1 \end{bmatrix}=\rho^{-1}r$ 。

其中，c = cos(θ), s = sin(θ) (θ = 2π/n) 。

为了符合更习惯的群符号，我们用 x 表示旋转 $\rho_{2\pi/n}$ ，用 y 表示反射 r 。

命题 6.4.3 二面体群 $D_{n}$ 阶为 2n 。它由两个元素 x 和 y 生成，且此二元素满足关系

$x^{n} = 1$ , $y^{2}=1$ , $yx = x^{-1}y$ 。

$D_{n}$ 的元素是

$1 \; , x \; , x^{2} \; , ... \; , x^{n-1} ; y \; , xy \; , x^{2y} \; , ... \; , x^{n-1}y$ 。

利用 (6.4.3) 的前两个关系式，第三个关系式可以按各种方式重写。相当于

(6.4.4) xyxy = 1 ，也相当于 $yx = x^{n-1}y$ 。

当 n = 3 时，这个关系式与对称群 $S_{3}$ (2.2.6) 的关系式一样。

推论 6.4.5 二面体群 $D_{2}$ 与对称群 $S_{3}$ 是同构的。

对于 n > 3 ，二面体群和对称群不是同构的，因为 $D_{n}$ 阶数为 2n ，而 $S_{n}$ 阶数为 n ! 。

当 n ≥ 3 时，二面体群 $D_{n}$ 的元素是正交算子，它们将一个正 n 边形 Δ 变换到其自身——即 Δ 的对称群。这不难看出，并且由定理可知：一个正 n 边形可以通过绕其中心旋转角度 2π/n 回到到自身，也可以通过一些反射回到自身。定理 6.4.1 将所有对称群粘合为 $D_{n}$ 。

二面体群 $D_{1}$ ， $D_{2}$ 太小，不能作为常规意义上的 n 边形对称群。 $D_{1}$ 是两个元素群 {1 ,r } 。因为它是一个循环群，如同 $C_{2}$ 。但 $D_{1}$ 的元素 r 是一个反射，而与 $C_{2}$ 中的幺元不同的元素是其角度为 π 的旋转。群 $D_{2}$ 包含4 个元素 { 1，ρ，r, ρr }，其中 ρ 是角度为 π 的旋转，而 ρr 是绕垂直轴的反射。该群与Klein四群同构。

若我们乐意，我们可以将 $D_{1}$ 和 $D_{2}$ 分别视为1 边和 2 边对称群：

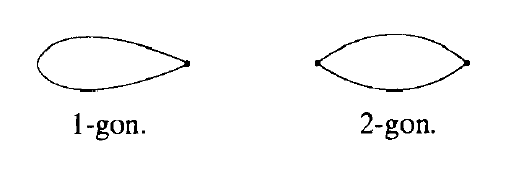
(译注：后缀“-gon” 本意是指角，但因边数和角数是相等的，因此我们称其为“边”。)

现在我们着手证明定理 6.4.1 。对于实数的可加群 $\mathbb{R}^{+}$ 的一个子群 Γ ，若存在一个(小的)正实数ε ，使得 Γ 的每一个非零元素 c 都有绝对值 ≥ ε ，则称其为一个离散群(discrete)。

引理 6.4.6 令 Γ 为可加群 $\mathbb{R}^{+}$ 的一个离散子群。则或者 Γ = 0 ，或者 Γ 是一个正实数 a 的整数集之集合 ℤa 。

证明：

此定理非常类似于定理 2.3.3 的证明， $\mathbb{Z}^{+}$ 的非零子群的形式为 ℤn 。

若 a 和 b 是 Γ 的不同元素，则由于 Γ 是一个群，则 a – b 在 Γ 中。且 | a – b |≥ ε 。Γ 的不同元素通过至少为 ε 的距离分隔。由于只有有限个以 ε 分隔的元素才能放入任何有界区间，因此有界区间包含Γ的有限个元素。

假设 Γ ≠ {0} 。则 Γ 包含一个非零元素 b ，且由于其是一个群，则 Γ 也包含 -b 。因此，其包含一个正元素，不妨设为 $a^{'}$ 。我们选择 Γ 中最小的正元素 a 。这是可行的，因为我们仅需在区间 $0 \leq x \leq a^{'}$ 中选择 Γ 的有限子区间的最小元素即可。

我们证明 Γ = ℤa 。由于 a 在 Γ 中且 Γ 是一个群，则 ℤa ⊂ Γ 。令 b 为 Γ 的一个元素。则对于某个实数，有 b = ra 。我们分出 r 的整数部分，记为 $r = m + r_{0}$ ，且 m 为一个整数，而 $0 \leq r_{0} < 1$ 。同样，由于 Γ 是一个群， $b^{' }= b -ma$ 位于 Γ 中且， $b^{'} = r_{0}a$ 。则 $0 \leq b^{'} < a$ 。由于 a 是 Γ 中的一个最小的正整数，则 $b^{'}$ 一定为零。因此，b = ma ，其位于 ℤa 中。从而 Γ = ℤa 。

定理 6.4.1 之证明：

令 G 为 $O_{2}$ 的一个有限子群。我们希望证明 G 是 $C_{n}$ 或 $D_{n}$ 。我们记得， $O_{2}$ 的元素是旋转 $\rho_{\theta}$ 和反射 $\rho_{\theta}r$ 。

第 1 种情况：G 的所有元素都是旋转。

我们必须证明 G 是一个循环。令 Γ 为一个实数 α 的使得 $\rho_{\alpha}$ 位于 G 中的集合。则 Γ 为加法群 $\mathbb{R}^{+}$ 的一个子群，其包含 2π 。由于 G 是有限的，则 Γ 是离散的。因此，Γ具有 ℤa 的形式。则 G 由扫过角度为 α 的整数倍的旋转构成。由于 2π 在 Γ 中，因此其为 α 的整数倍。从而对于某个整数 n ，有 α = 2π/n ，且 $G=C_{n}$ 。

第 2 种情况：G 包含一个反射。

我们调整我们的坐标，使处标准反射r位于 G 中。令 H 表示来自 G 的元素的旋转构成的子群。我们应用我们在情况1 中已证明的结论推导出 H 是由 $\rho_{\theta}$ 生成的循环群(对于某个角 θ = 2π/n )。则 2n 个幂 $\rho_{\theta}^{k}$ 和乘积 $\rho_{\theta}^{k}r$ 位于G 中(0 ≤ k < n - 1)，因此，G 包含二面体群 $D_{n}$ 。我们断言 $G=D_{n}$ ，为了证明此断言，我们取 G 的任意元素 g 。则 g 为一个旋转或一个反射。若 g 是一个旋转，则根据 H 的定义，g 在 H 中。H 的元素也位于 $D_{n}$ 中，因此 g 在 $D_{n}$ 中。若 g 是一个反射，则对于某一个旋转 $\rho_{\alpha}$ ，我们将其记为 $\rho_{\alpha}r$ 。由于 r 在 G 中，因此乘积 $gr=\rho_{\alpha}$ 也在 G 中。从而 $\rho_{\alpha}$ 是 $\rho_{\theta}$ 的幂，同样，g 在 $D_{n}$ 中。

定理 6.4.7 (定点定理(Fixed Point Theorem)) 令 G 为平面之等距的一个有限群。则平面中存在一个由 G 中的每一个元素所固定的点，即一个点定点 p，其使得对于 G 中的所有 g，有 g(p) = p 。

证明：

这是一个巧妙的几何论证。令 s 为平面上的任意一点，并令 S 为 s 在 G 中各种等距下的像构成的点之集合。因此，S 中的每一个元素 $s^{'}$ 都具有形式 $s^{'}=gs$ ，其中 g 是 G 中的某一个元素。这个集合称为 s 在 G 作用下的轨道(orbit)。元素 s 位于轨道中，因为单位元 1 在 G 中，且 s = l(s)。下图描绘了 G 作为正五边形对称群的典型轨道，以及该作用的定点 p 。

G 的任意元素都会置换 S 的轨道。换言之，若 $s^{'}$ 在 S 中且 s 在 G 中，则 $h(s^{'})$ 在 S 中：比如 $s^{'}=g(s)$ ，而 g 在 G 中。由于 G 是一个群，因此 hg 位于 G 中。则 hg(s) 位于 S 中且等于 $h(s^{'})$ 。

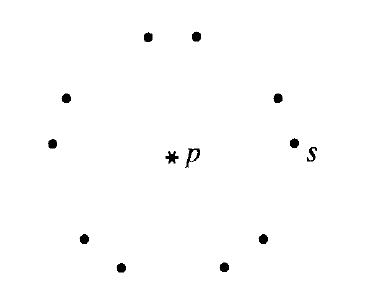
我们任意列出 S 的元素，记为 $S = \{ s_{1} ,..., s_{n} \}$ 。则我们寻求的定点是形心(或质心)(centroid)(译注：几何中心或图形中心) 或重心(center of gravity)，定义为

(6.4.8) $p = \frac{1}{n}( s_{1} + ...+ s_{n} )$ ，

其中，公式的右侧按向量加计算，在平面中使用任意坐标系统。

引理 6.4.9 等距将形心(图形之中心)带到形心。令 $S = \{ s_{1} ,..., s_{n} \}$ 为平面的一个有限点集，并令 p 为其形心，如 (6.4.8) 所定义。令 m 为一个等距。令 $m(p)=p^{'}$ 和 $m(s_{i}) = s_{i}^{'}$ 。则 $p^{'}$ 是集合 $S^{'} = \{ s_1^{'} ,..., s_n^{'} \}$ 的形心。

集合 S 的形心是一个定点可推导。G 中的一个元素 g 置换了轨道 S 。它将 S 映射到 S，从而将 p 映射到 p 。

引理 6.4.9 之证明：

这可以通过物理推理推导出来，也可以用代数方法证明。为此，只需分别考察 $m=t_{a}$ 和 m = φ 的情况即可，其中 φ 是一个正交算子。任何等距都可以通过复合这样的等距而获得。

第1种情况： $m=t_{a}$ 是一个平移。

则 $s_{i}^{'} = s_{i} + a$ ， $p^{'} = p + a$ 。则有

$p^{'} = p + a = \frac{1}{n} \left ( ( s_{1} + a )+... + ( s_{n} + a ) \right ) = \frac{1}{n} ( s_1^{'} + ... + s_n^{'} )$ 。

第2 种情况：m = φ 是一个线性算子。

$\begin{array}{rlc} p^{'} = {\varphi}(p) \! &= {\varphi}(\frac{1}{n}( s_{1} + ... + s_{n} )) = \frac{1}{n}( {\varphi}(s_{1}) + ... + {\varphi}(s_{}) ) \\ \\ &= \frac{1}{n} ( s_{1}^{'} + ... + s_{n}^{'} ) \end{array}$ 。

结合定理 6.4.1 和 6.4.7，我们可以得到平面有界图形的对称群的描述。

推论 6.4.10 令 G 为平面之等距的群 M 的一个有限子群。若选择合适的坐标，则 G 就会成为定理 6.4.1 所描述的群 $C_{n}$ 或 $D_{n}$ 之一。

6.5 离散等距群(Discrete groups of isometries)

在本节中，我们将讨论无界图形的对称群，例如图 6.1.5 所示的图形。我称之为万花筒原理(kaleidoscope principle)，可以用来构造具有已知对称群的图形。你可能已经看过万花筒了。人们在管子的末端看到一个扇形，其侧面由两面镜子界定，这两面镜子沿着管子的长度延伸，并按 θ 的角度放置，例如 θ = π/6 。人们还会在每个镜子中看到扇形的反射，然后看到反射的反射，依此类推。扇形中通常有一些彩色玻璃碎片，它们的反射形成一种图案(pattern)。

这涉及到一个群。在万花筒末端的平面上，令 $\ell_{1}$ 和 $\ell_{2}$ 为界定由镜子组成的扇形的直线。这个群是二面体群，由围绕 $\ell_{i}$ 的反射 $r_{i}$ 生成。这两个反射之积 $r_{1} r_{2}$ 保向且固定了两条直线的交点，因此其为一个旋转。其旋转角是 ±2θ 。

同样的原理可以应用到 M 的任何子群 G 。我们不会给出证明的确切推理，但这种方法可以做到精确。我们从平面上的一个随机图形 R 开始。我们的群 G 的每一个元素 g 都将 R 移动到一个新的位置，我们称其为 gR 。图形 F 是所有图形 gR 的并集。群中的元素 h 将 gR 映射作为F 的一部分的 hgR ，因此它将 F 映射到自身。如果 R 足够随机，G 将是 F 的对称群。正如我们从万花筒中所知，图形 F 通常非常具有吸引力。当 G 是正五边形的对称群时，应用此方法的结果如下所示。

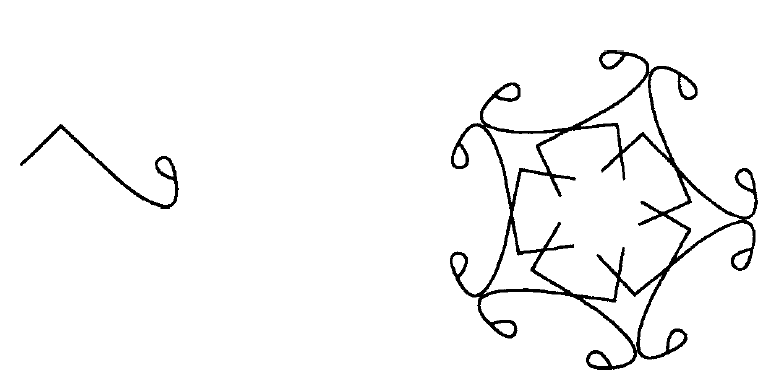
当然，许多不同的图形都有相同的对称群。但描述这些群既有趣又有益。我们将提出一个粗略的分类，并在习题中进行完善。

M 中的一些子群过于复杂(wild)，无法形成合理的几何结构。例如，如果万花筒中镜子的摆放角度 θ 不是 2π 的比率数(rational)倍数，那么该扇形将有无穷多个不同的反射。我们需要排除这种可能性。

定义 6.5.1 如果平面 P 的等距变换群 G 不包含任意小的平移或旋转，则该群是离散的。更确切地说，如果存在一个正实数 ε 满足以下条件，则 G 是离散的：

(a) 若 G 的一个元素是按一个非零向量 a 的平移，则 a 的长度至少是 ε ：|a| ≥ ε ，和

(b) 若 G 的一个元素是一个围绕某个点扫过角度 θ 的旋转，则 θ 的绝对值至少是 ε ：|θ| ≥ ε 。

注意：由于平移向量和旋转角度构成不同的集合，因此，为它们分别设置下界似乎更为合适。然而，在这个定义中，我们并不关心向量和角度的最佳界限，因此我们选择足够小的 ε，以便同时兼顾两者。

平移和旋转都是保向等距变换(6.3.4)，这些条件适用于所有保向等距变换。我们不对方向反转等距变换施加条件。如果 m 是具有非零滑移向量 v 的滑射，则 $m^{2}$ 是平移 $t_{2v}$ 。因此，基于平移向量的下限也决定了滑移向量的界限。

分析一个离散群 G 有三种方法：

• 平移群 L ——平移向量的群 V 的一个子群。

• 点群 $\overline{G}$ ——正交群 $O_{2}$ 的一个子群。

• $\overline{G}$ 在 L 上的一个运算。

平移群：

G 的一个平移群 L 是一个向量 v 的使得平移 $t_{v}$ 位于G 中的集合。即

(6.5.3) $L = \{ v \in V | t_{v} \in G \}$ 。

由于 $t_{v} t_{w} = t_{v+w}$ 和 $t_{v}^{-1} = t_{-v}$ ，L 是所有平移向量的可加群 $V^{+}$ 的一个子群。G 中基于平移的边界 ε 界定了 L 中向量的长度：

(6.5.4) L 中每一个非零向量 v 都具有长度 | v | ≥ ε 。

• 对于任意 ε > 0 ，满足条件 (6.5.4) 的可加群 $V^{+}$ 或 $\mathbb{R}^{+}$ 之一的一个子群 L 称为一个离散子群。(这是之前对 $\mathbb{R}^{+}$ 的定义。)

当且仅当 L 的不同向量 a 和 b 之间的距离至少为 ε 时，子群 L 是离散的。这是成立的，因为这个距离是 b–a 的长度，而 b–a 位于 L 中，因为 L 是一个子群。若 (6.5.4) 成立，则 | b–a |≥ ε 。

定理 6.5.5 $V^{+}$ 或 $\mathbb{R}^{+}$ 的每一个子群都是下列群之一：

(a) 零群 L = {0} 。

(b) 一个非零向量 a 的整数位之集合：

L = ℤa = { ma | m∈ℤ } ，或

L = ℤa + ℤb = { ma + nb | m, n∈ℤ } 。

上述所列的第三种类型的群称为晶格(lattices)，而生成集 (a , b) 称为晶格基(lattice basis)。

(6.5.6) 一个日格图：

引理 6.5.7 令 L 为 $V^{+}$ 或 $\mathbb{R}^{+}$ 的一个离散子群。

(a) 一个平面的有界区域仅包含有限多个 L 的点。

(b) 若 L 不是平凡群，则其包含最小长度的非零向量。

证明：

(a) 由于 L 中的元素之间至少相距 ε ，因此一个小正方形最多只能包含 L 中的一个点。如果平面上的一个区域被某个大矩形所包含，则该区域有界。我们可以用有限多个小正方形覆盖任意矩形，每一个小正方形最多包含 L 中的一个点。

(b) 如果 L 中不包含更短的非零向量，则我们称向量 v 为 L 中最小长度的非零向量。为了证明这样的向量存在，我们假设 L 不是平凡群。L 中存在非零向量 a 。那么，关于原点半径为 |a| 的圆盘是一个有界区域，包含 a 和 L 中有限多个其他非零点。其中一些点的长度将最小。

已知 $\mathbb{R}^{2}$ 的一个基 B = (u , w) ，我们令 π(B) 表示具有顶点 0，u ,w ,u + w 的平行四边形。它由线性组合 ru + sw( 0 ≤ r ≤ 1 , 0 ≤ s ≤ 1 ) 构成。此外，我们用 $\pi^{'}(\mathbf{B})$ 表示通过从 π(B) 删除掉两条边 [ u ,u + w ] 和 [ w ,u + w ] 而获得的区域。它由线性组合 ru + sw( 0 ≤ r < 1 , 0 ≤ s < 1 ) 构成。

引理 6.5.8 令 B = (u , w) 为 $\mathbb{R}^{2}$ 的一个基，并令 L 为 B 的整数组合的晶格。 $\mathbb{R}^{2}$ 中的每一个向量 v 都可以唯一地记为 $v = x + v_{0}$ 的形式，且 x 在 L 中且 $v_{0}$ 在 $\pi^{'}(\mathbf{B})$ 中。

证明：

由于 B 是一个基，每一个向量都是一个线性组合 ru + sw ，且系数 r 和 s 为实数。我们分出其整数部分，分别记为 $r = m + r_{0}$ 和 $s = n + s_{0}$ ，其中m ，n 为整数且 $0 \leq r_{0} ,s_{0} < 1$ 。则 $v = x + v_{0}$ ，其中，x = mu + nv 位于 L 中，且 $v_{0} = r_{0}u + s_{0}w$ 位于 $\pi^{'}(\mathbf{B})$ 。对此，只有一种实现方法。

定理 6.5.5 之证明：

只需考虑 $\mathbb{R}^{2}$ 的一个离散子群 L 即可。L是零群的情况包含于列表中。若 L ≠ {0}，则存在两种可能性：

第1种情况： L 中的所有向量都位于经过原点的一条直线 𝓁 上。

则 L 是 $\ell^{+}$ 的可加群的一个子群，其与 $\mathbb{R}^{+}$ 同构。根据引理 6.4.6 ，L 具有 ℤa 的形式。

第2种情况：L的元素不位于一条直线上。

在这种情况下，L包含线性无关向量 $a^{'}$ 和 $b^{'}$ ，则 $B^{' }= (a^{'} , b^{'} )$ 是 $\mathbb{R}^{2}$ 的一个基。我们必须证明存在 L 的一个晶格基。

我们首先考虑由 $a^{'}$ 张成的直线 𝓁 。 $\ell^{+}$ 的子群 L∩𝓁 是离散的，且 $a^{'}$ 不为零。因此，根据情况 1 中已证明的结论，L 的形式为 ℤa，其中 a 为向量。我们调整坐标并重新缩放，使 a 变为向量 $(0,1)^{t}$ 。

现在，若有必要，我们用 $-b^{'}$ 替换 $b^{'}=(b_{1}^{'},b_{2}^{'})^{t}$ ，因此 $b_{2}^{'}$ 成为正数。我们寻求 L 中的一个向量 $b=(b_{1},b_{2})^{t}$ 且 $b_{2}$ 为正数且尽可能小。先验地，我们有无穷多个元素需要检查。然而，由于 $b^{'}$ 在 L 中，我们只需要检查满足 $0 < b_{2} \leq b_2^{'}$ 的元素 b 。此外，我们可以将 a 的倍数添加到 b 中，因此我们也可以假设 $0 < b_{1} < 1$ 。这样做之后，b 将位于一个有界区域内，该区域包含 L 中有限多个元素。我们遍历这个有限集以求得所需的元素 b ，并证明 B = (a, b) 是 L 的晶格基。

令 $\widetilde{L} = \mathbb{Z}a + \mathbb{Z}b$ 。则 $\tilde{L} \subset L$ 。我们必须证明 L 的每一个元素都位于 $\tilde{L}$ 中。将引理 6.5.8 应用于 $\tilde{L}$ ，则只需证明 L 在区域 $\pi^{'}(\mathbf{B})$ 中的唯一元素是零向量即可。令 $c = (c_{1},c_{2})^{t}$ 为 L 的位于那个区域中的一个点。因此， $0 \leq c_{1} < 1$ 且 $0 \leq c_{2} < b_{2}$ ，由于 $b_{2}$ 选择得足够小，则 $c_{2}=0$ ，且 c 位于直线 𝓁 上。则 c 是 a 的一个整数倍，且由于 $0 \leq c_{1} < 1$ ，从而 $c_{1}=0$ 。

点群：

现在我们转向分析离散等距群的第二个工具。我们选择坐标系，并回到同态 $\pi :{M} \longrightarrow O_{2}$ ，其核是平移群T (6.3.10)。当我们将此同态限定为离散子群G 时，我们得到一个同态

(6.5.9) ${\pi}|_{G}: \longrightarrow O_{2}$ 。

点群 $\overline{G}$ 是 G 在正交群 $O_{2}$ 中的像。明确区分群 G 的元素和其点群 $\overline{G}$ 的元素非常重要。因此，为了避免混淆，当符号表示 $\overline{G}$ 中的元素时，我们会在它们上面加上横线。对于 G 中的 g ， $\overline{g}$ 将是一个正交算子。

根据定义，若 G 包含一个形如 $t_{a}\rho_{\theta}$ 的元素，则一个旋转 $\overline{\rho}_{\theta}$ 位于 $\overline{G}$ 中。这是一个围绕平面的同一个点扫过同一个角 θ 的旋转(6.3.5) 。 $\overline{G}$ 的一个元素 $\overline{\rho}_{\theta}$ 在 G 中的一个逆向由 G 的关于平面的各个点扫过角度 θ 的旋转构成。

类似地，令 𝓁 表示 $\rho_{\theta}r$ 的反射直线。正如我们前面所注意到的那样，基关于 $e_{1}$ 轴的角度是 $\frac{1}{2}\theta$ (5.1.17) 。若在 G 中存在一个元素 $t_{a}\rho_{\theta}r$ ，则点群 $\overline{G}$ 包含 $\overline{\rho_{\theta}r}$ ，且 $t_{a}\rho_{\theta}r$ 是一个沿一条与 𝓁 平行的直线的反射或滑射(6.3.8)。 $\overline{\rho_{\theta}r}$ 的逆像由 G 的沿与 𝓁 平行的直线的反射或滑射的所有元素构成。总结就是：

• 点群 $\overline{G}$ 记录了 G 的元素的反射线和滑射线的旋转角和斜率。

命题 6.5.10 $O_{2}$ 的离散子群 $\overline{G}$ 是有限的，从而此子群要么是循环的要么是二面体的。

证明：

由于 $\overline{G}$ 不包含小的旋转，使得 $\rho_{\theta}$ 位于 $\overline{G}$ 中的实数 θ 之集合 Γ 是可加群 $\mathbb{R}^{+}$ 的包含 2π 的一个离散子群。根据引理 6.4.6 ， Γ 具有 ℤθ 形式，其中，θ = 2π/n (对于某一个整数 n )。至此，定理 6.4.1 的证明完成。

晶体约束 (The Crystallographic Restriction)

若一个离散等距群 G 的平移群是平凡群，则 π 对 G 的约束将是单射。在这种情况下，G 将同构于其点群 $\overline{G}$ ，并且将是循环的或二面体的。下一个命题是我们分析无限离散群的第三个工具。它将点群与平移群联系了起来。

除非选择一个原点，否则正交群 $O_{2}$ 不会基于平面 P 操作。但确实会基于平移向量的空间 V 操作。

命题 6.5.11 令 G 为 M 的一个离散子群。令 a 为其平移群 L 的一个元素，并令 $\overline{g}$ 为点群 $\overline{G}$ 的一个元素。则 $\overline{g}(a)$ 位于 L 中。

我们可以重述这个命题，称 $\overline{G}$ 的元素将 L 映射到其自身。则当 L 视为平面 V 中的一个图形时， $\overline{G}$ 含于 L 的对称群中。

命题 6.5.11 之证明：

令 a 和 g 分别为 L 和 G 的一个元素，令 $\overline{g}$ 为 $\overline{G}$ 中 g 的像，并令 $a^{'}=\overline{g}(a)$ 。我们将证明 $t_{a^{'}}$ 是共轭 $gt_{a} g^{-1}$ 。这将证明 $t_{a^{'}}$ 位于 G 中，从而 $a^{'}$ 在 L 中。我们记 $g = t_{b}\varphi$ 。则 φ 位于 $O_{2}$ 中且 $\overline{g}=\overline{\varphi}$ 。因此 $a^{'}=\overline{\varphi}(a)$ 。利用公式 (6.2.8),求得：

$gt_{a} g^{-1} = (t_{b}{\varphi}) {\varphi}(g^{-1} t_{-b}) = t_{b} t_{a^{'}}{\varphi}{\varphi}^{-1} t_{-b} = t_{a^{'}}$ 。

注意：重要的是要理解群 G 不作用于它的平移群 L 。事实上，问 G 是否作用于 L 是没有意义的，因为 G 的元素是平面 P 的等距，而 L 是 V 的子集。除非原点固定，否则 P 不等于 V。如果我们固定 P 中的原点，我们就可以将 P 等同于 V 。那么这个问题就有意义了。我们可以问：P 中是否存在一个点，使得以该点为原点，G 的元素将 L 带向自身？有时是，有时不是。这取决于群。

下一个定理描述了当平移群 L 不是平凡时可能出现的点群。

定理 6.5.12 (晶体约束) 令 L 为 $V^{+}$ 或 $\mathbb{R}^{+}$ 的一个离散子群，并令 $H\subset O_{2}$ 为 L 的对称群的一个子群。假设 L 不是平凡群，则：

(a) H 中的每一个旋转都具有阶 1，2，3，4 或 6，和

(b) H 是群 $C_{n}$ 和 $D_{n}$ 之一，且 n = 1，2，3，4 或 6 。

特别是，5阶旋转被排除。不存在具有五重旋转对称性的壁纸图案(具有五重对称性的“准周期”图案确实存在。例如，参见[Senechal]。)

定理 6.5.12 (晶体约束) 之证明：

我们证明 (a)。(b) 部分由 (a) 和定理 6.4.1 得出。设 ρ 为 H 中扫过角度为 θ 的旋转，a 是 L 中长度最小的非零向量。由于 H 作用于 L，则ρ(a) 也位于 L 中。且由于 a 具有最小长度，则 b = ρ(a) - a 也位于 L 中，且 | b |≥| a |。观察下图，可知当 θ < 2π/6 时，| b | < | a | 。因此，我们一定有 θ ≥ 2π/6 。由此可知，群 H 是离散的，因此是有限的，且 ρ 的阶为 6 。

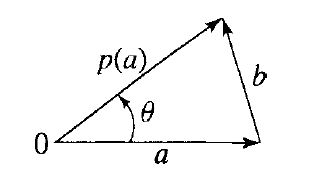
θ = 2π/5 的情况也可以排除，因为对于那个角，元素 $b^{'} = {\rho}^{2}(a) + a$ 比 a 更小。

6.6 平面晶体群(Plane crystallographic groups)

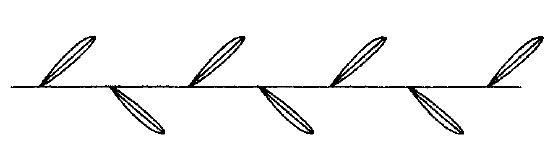
我们回到我们的等距离散群 G ⊂ M 。我们已经看到，当 L 为平凡群时，G 是循环群或二面体群。使得 L 为无限循环群 (6.5.5)(b) 的离散群 G是饰带图案(frieze patterns)的对称群，例如 (6.1.3)，(6.1.4) 中所示的那些群。我们将这些群的分类留作习题。

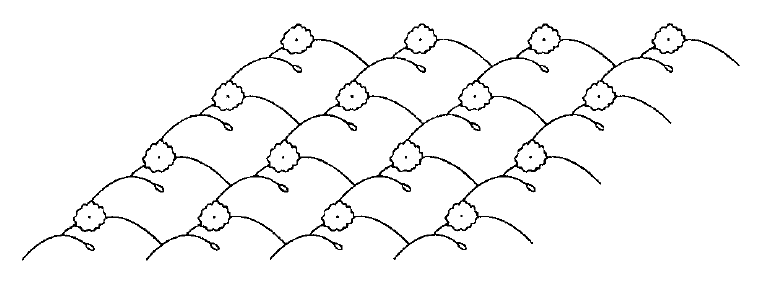
当L为晶格时，G称为二维晶体群。这些晶体群是二维晶体(two-dimensional crystallographic group)(例如石墨)的对称群。我们假设晶体无限大。分子规则排列的事实意味着它们形成具有两个独立平移对称性的阵列。墙纸图案也会在两个不同的方向上重复出现——一次沿着纸条，因为图案是用滚筒印制的；另一次是因为纸条是并排粘在墙上的。晶体的约束限制了可能性，并使得人们可以将晶体群分为17种类型。图(6.6.2)展示了各种对称类型的代表性图案。

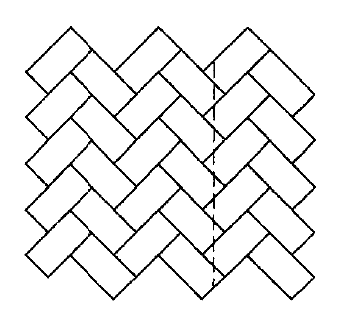
点群 $\overline{G}$ 和平移群 L 不能完全确定 G ，因为 $\overline{G}$ 中的反射不一定是 G 中反射的像，这使得事情变得复杂。它可能在G中仅通过滑动来表示，就像下面所示的砖块图案一样。这个图案(我最喜欢的)相对微妙，因为它的对称群不包含反射。它具有以角度为π 绕每一个砖块的中心旋转的旋转对称性。所有的这些旋转都表示点群 $\overline{G}$ 的同一个元素 $\overline{\rho}_{\pi}$ 。不存在旋转角为0和π之外的其他角度的非平凡旋转对称性。该图案还具有沿图中虚线滑动的对称性，因此， $\overline{D}=D_{2}=\{1\; ,\overline{ {\rho}{\pi}} \; , \overline{r}\;,\overline{\rho_{\pi}r} \}$ 。

只需两步，就能相当轻松地确定一个图案的点群：首先寻找旋转对称。旋转对称性通常比较容易找到。在点群 $\overline{G}$ 中的一个旋转 $\overline{\rho}_{\theta}$ 由一个图案的对称群 G 中具有同样角度的旋转表示。当求得了这个旋转对称，我们就会知道使得这个点群是 $C_{n}$ 或 $D_{n}$ 的整数 n 。然后通过观察图案是否具有反射或滑动对称性，将 $C_{n}$ 和 $D_{n}$ 区分出来。若存在，则 $\overline{G}=D_{n}$ ，否则 $\overline{G}=C_{n}$ 。

点群中具有四重旋转的平面晶体群(Plane Crystallographic Groups with a Fourfold Rotation in the Point Group)

作为对等距散群进行分类的方法的一个例子，我们分析点群为 $C_{4}$ 或 $D_{4}$ 的群。

令 G 为这样的一个群，令 $\overline{\rho}$ 表示 $\overline{G}$ 中角度为 π/2 的旋转，并令 L 为G的晶格，即使用得 $t_{v}$ 位于 G 中的向量 v 的集合。

引理 6.6.2 晶体 L 是方的。

证明： 我们选择一个 L 中的具有最小长度的非零向量 a 。这个点群作用于 L 上，因此 $\overline{\rho}(a)=b$ 位于 L 中且与 a 正交。我们断言，( a , b ) 是 L 的晶格基。

假设不是这样。则根据引理 6.5.8 ，在由点 $r_{1}a + r_{2}b$ ( $0 \leq r_{i} < 1$ ) 组成的区域 ${\pi}^{'}$ 中将存在 L 的一个点，这样的一个点 w 与正方形四个顶点 0，a，b，a + b 之一的距离小于 |a|。该顶点记为 v 。则 v - w 也在 L 中，且 |v - w| < |a|。这与 a 的选择相矛盾。

我们选择一个坐标系并重新缩放，以便 a 和 b 成为标准基向量 $e_{1}$ 和 $e_{2}$ 。则 L 成为具有整数坐标的向量晶格，则 ${\pi}^{'}$ 成为向量集 $(s,t)^{t}$ ( 0 ≤ s < 1 且 0 ≤ t < 1 )。

这确定了平面 P 中关于平移的坐标。

(6.6.2) 17 个平面晶体群的样本图案。

基于 V 的将 L 映射到其自射的正交算子构成了二面体群 $D_{4}$ ，其由扫过角度 π/2 的旋转 $\overline{\rho}$ 和标准反射 $\overline{\rho}$ 生成。我们假设 $\overline{\rho}$ 位于 $\overline{G}$ 中。若 $\overline{r}$ 也在 $\overline{G}$ 中，则 $\overline{G}$ 是二面体群 $D_{4}$ 。否则， $\overline{G}$ 是循环群 $C_{4}$ 。当 $\overline{G}$ 是循环群 $C_{4}$ 的时候，我们先描述群 G 。令 g 为 G 的一个元素，其在 $\overline{G}$ 中的像是旋转 $\overline{\rho}$ 。则 g 是平面中一个绕平面中某一点 p 的扫过角度 π/2 的旋转。我们平移平面中 P 的坐标使得 p 点成为原点。在这个坐标系统中，G 包含绕原点的旋转 $\rho = \rho_{\pi/2}$ 。

命题 6.6.3 令 G 为一个其点群 $\overline{G}$ 是循环群 $C_{4}$ 通过坐标选择使得 L 是具有整数坐标的点之晶格，并使得 $\rho = \rho_{\pi/2}$ 是 G 的一个元素，群 G 由积 $t_{v}\rho_{i}$ 构成，且 v 位于 L 中而 0 ≤ i < 4 ：

$G = \{ t_{v} {\rho}^{i} | v{\in} L \}$ 。

证明：

令 $G^{'}$ 表示形如 $t_{v}{\rho}^{i}$ ( v∈L )的元素集。我们必须证明 $G^{'} = G$ 。根据 L 的定义， $t_{v}$ 位于 G 中，此外，ρ 位于 G 中。因此 $t_{v}{\rho}^{i}$ 位于 G 中，从而 $G^{'}$ 是 G 的子集。

为了证明相反的结论，令 g 为 G 的任意元素。由于点群 $\overline{G}$ 是 $C_{4}$ , 故 G 的每一个元素都是保向的。因此，对于平移向量 u 和某个角度 α ，g 具有 $g = t_{u}\rho_{\alpha}$ 的形式。这个元素在点群中的像是 $\overline{\rho}_{\alpha}$ , 因此，α 是 π/2 的倍数。且对于某个 i , 有 $\overline{\rho}_{\alpha}=\rho^{i}$ 。由于 ρ 在 G 中，则 $g{\rho}^{-i} = t_{u}$ 位于 G 中，而 u 在 L 中。从而 g 位于 $G^{'}$ 中。

现在我们考虑点群 $\overline{G}$ 是 $D_{4}$ 的情况。

命题 6.6.4 令 G 为一个平面晶体群，其点群 $\overline{G}$ 是二面体群 $D_{4}$ 。设所选择的坐标使得 L 是具有整数坐标的点之晶格，且使得 $\rho = \rho_{\pi/2}$ 为 G 的一个元素。此外，令 c 表示向量 $(\frac{1}{2},\frac{1}{2})^{t}$ 。则存在两种可能：

(a) G 的元素是乘积 $t_{v}{\varphi}$ (共中 v 在 L 中而 φ 在 $D_{4}$ 中)，即

$G = \{t_{v} {\rho}^{i} | v\in L \} \cup \{t_{v} {\rho}^{i}r | v\in L \}$ ，或

(b) G的元素是乘积 $t_{x}{\varphi}$ (共中 φ 在 $D_{4}$ 中)。则 φ 是一个旋转，则 x 在L 中，而若 φ 是一个反射，则 x 在陪集(coset) c + L 中:

$G = \{t_{v} {\rho}^{i} | v\in L \} \cup \{t_{u} {\rho}^{i}r | u\in c+L \}$ 。

证明：

设 H 是 G 中保向等距的子集。它是 G 的一个子群，其平移格为 L，且包含 p 。因此，它的点群为 $C_{4}$ 。根据 6.6.3 ，由 H 由 $t_{v} {\rho}^{i}$ ( v 在 L 中) 组成。

点群也包含 $\overline{r}$ 。我们选择 G 中的一个元素g ，使得 $\overline{g}=\overline{r}$ 。对于某个向量 u ，其将具有 $g=t_{u}r$ 的形式，但我们不知道 u 是否在 L 中。

我们可以将左边的 g 乘以 G 中的平移 $t_{v}$ (即，v 位于 L 中)，将 u 移入 0 ≤ p, q < 1 的点的区域 $\pi^{'}$ 。我们假设这一步已完成。

根据 $g = t_{u}r$ 并利用公式(6.3.3)计算得到：

$g^{2} = t_{u}rt_{u}r = t_{u+ru}$ 和 $(g\rho)^{2} = (t_{u}r\rho)^{2} = t_{u+r{\rho}u}$ 。

这些是 G 的元素，因此 $u + ru = (2p,0)^{t}$ ，以及 $u + r{\rho}u = (p-q,p-q)^{t}$ 位于晶格 L 中。它们是具有整数坐标的向量。由于 0 ≤ p, q < 1 且 2p 是一个整数，则 p 为 0 或 $\frac{1}{2}$ 。由于 p – q 也是一个整数，若p = 0 则 q = 0 ，而若 $p=\frac{1}{2}$ 则 $q=\frac{1}{2}$ 。因此，对于 u 仅有两种可能性： $u=(0,0)^{t}$ 或 $u=c=(\frac{1}{2},\frac{1}{2})^{t}$ 。在第一种情况下，g = r , 因此，G 包含一个反射。这是命题中的情况 (a) 。第二种可能性是情况 (b)。

6.7 抽象对称性：群运算(Abstract symmetry:group operations)

群的概念可以应用到几何图形之外的事物。例如，复共轭 (a + bi) ⇝ (a - bi) 可以视为复数的一个对称。由于复共轭与加法和乘法兼容，它称为域 ℂ 的一个自同构(automorphism)。从几何学上讲，它是复平面关于实轴的双侧对称性，但它是自同构的说法是指它的代数结构。域 $F = \mathbb{Q}[\sqrt{2}]$ 也有一个同构，其元素是形如 $a+b\sqrt{2}$ ( a和b 是比率数(rational )), 此同构映射 $(a + b\sqrt{2}) \rightsquigarrow (a - b\sqrt{2})$ 。这不是一个几何对称性。

另一个抽象“双侧”对称的例子是3阶循环群H 。它有一个可以互换不同于幺元的两个元素的自同构。一个代数结构 X (例如一个群或一个域)的自同构集构成一个群，其合成律为映射合成。每一个自同构都应该视为 X 的一个对称，即它是 X 的一个与其代数结构兼容的元素的一个置换。但在这种情况下，其结构是代数的，而不是几何的。

因此，“自同构(automorphism)”和“对称性(symmetry)”这两个词在一定意义上是同义词，只是“自同构”用于描述保留代数结构的集合的一个置换，而“对称性”通常(但并非总是)指保留几何结构的置换。

自同构和对称性都是更一般的群运算概念的特例。群 G 在集合 S 上的运算是一个法则，这个法则将G 中的一个元素 g 与 S 中的一个元素 s 组合得到 S 中另一个元素。换言之，它是一个映射 G × S ⟶ S 。我们暂且将此法则应用于元素 g 和 s 后产生的结果记为为 g * s 。运算需要满足以下公理：

例子 6.7.1：

(a) 对于 S 中的所有 s，有 1* s = s (1 在此指 G 的幺元，而不是仅指数字1) 。

(b) 结合律：对于 G 中的所有 g 和 $g^{'}$ 以及 S 中的 s ，有 $(gg^{'})*s = g(g^{'}s)$ 。

群作用于集合的例子随处可见(manywhere)(注：数学家永田正义(Masayoshi Nagata)在写书时，认定英语需要这个词；后来他真的在一本字典里找到了它)，而且通常情况下，运算的公理显然成立。平面等距群 M 作用于平面上的点集。它也作用于平面上的线集和三角形集。对称群 $S_{n}$ 作用于索引集 { l, 2 , ..., n }。

这样的定律称为运算的原因在于：若我们固定 G 的一个元素 g ，但令 S 中的 s 变动，则左乘 g (或g的运算) 定义了一个从 S 到其自身的映射。这个映射描述了元素 g 运算的方法，我们用 $m_{g}$ 来表示这个映射：

(6.7.2) $m_{g}:S \longrightarrow S$

是一个由 $m_g(s)=gs$ 定义的映射。它是 S 的一个置换，是一个双射，因为它有一个逆函数 $m_{g^{-1}}$ : 用 $g^{-1}$ 相乘的乘法运算。

• 已知一个群 G 基于一个集合 S 的一个运算，通过群运算，S 的一个元素s 将映射到各种其它元素。我们在这些元素收集在一起，就获得了一个子集，称其为 s 的轨道，记为 $O_{s}$ :

(6.7.3) $O_{s} = \{ s^{'}\in S | s^{'} = gs ($ 对于 G 中的某个 g $) \}$ 。

当平面的等距群 M 基于平面上的一个三角形之集合 S 运算时，已知三角形 $\triangle$ 的轨道 $O_{\triangle}$ 与三角形 $\triangle$ 全等。当我们证明了平面上的一个有限群 (6.4.7)的运算的定义存在时，又会引入另一个轨道。

群行为的轨道是等价关系

(6.7.4) $s \sim s^{'}$ ( 若 $s^{'} = gs$ 和 G 中的某个 g )

的等价类。因此，若 $s \sim s^{'}$ ，即若对于 G 中的某个 g 有 $s^{'}=gs$ ，则 s 和 $s^{'}$ 的轨道是相同的。由于它们是等价类，则有

(6.7.5) 轨道分割集合 S 。

该群在每个轨道上独立运算。例如，平面上的三角形集合划分为全等类，并且等距分别对每一个全等类进行置换。

如果S 仅由一条轨道组成，则G的运算称为可传递的。这意味着S中的每一个元素都被群中的某一个元素传递到其他每一个元素。对称群 $S_{n}$ 在索引集{ l , … , n } 上可传递地运算。平面等距群M在平面点集上可传递地运算，并且在直线集上可传递地运算。但它在三角形集上不传递运算。

• S 的一个元素 s 的稳定器(stabilizer)是使 s 固定的群元素的集合。其是G的一个子群，我们通常用 $G_{s}$ 表示：

(6.7.6) $G_{s}= \{ g \in G | gs = s \}$ 。

例如，在基于平面点集的群 M 的运算中，原点的稳定器与正交算子群 $O_{2}$ 同构。对称群 $S_{n}$ 的运算的索引 n 的稳定器与 {1 , … , n – 1 } 的排列的子群 $S_{n-1}$ 同构。或者，若 S 是平面中的三角形集，则一个特殊等边三角形 $\triangle$ 是其一个对称群，即 M 的一个同构于二面体群 M 的子群。

注意：务必明确以下区别：当我们说一个等距m使三角形 $\triangle$ 稳定时，我们并非指m 固定了 △ 的点。唯一能固定三角形每一个点的等距是恒等映射。我们指的是，在对三角形集合进行排列(或置换)时，m 将A带向自身。

正如一个群同态 $\varphi :G \longrightarrow G^{'}$ 的核 K 告诉我们何时 G 的两个元素 x 和 y 具有相同的像(即 $x^{-1}y$ 位于 K 中)那样，S 的一个元素 s 的稳定器告诉我们何时G 的两个元素 x 和 y 按相同的方式作用于 s 。

命题 6.7.7 令 S 为一个群 G 在其上运算的集合，令 s 为 S 的一个元素，并令 H 为 s的一个稳定器。则

(a) 若 a 和 b 是 G 的元素，则当且仅当 $a^{-1}b$ 位于 H 中时，有as = bs ，且当且仅当 b 位于陪集 aH 中时其也立。

(b) 假设 $as = s^{' }$ 。则 $s^{' }$ 的稳定器 $H^{'}$ 是一个其轭子群：

$H^{'} = aHa^{-1} = \{ g\in G | g = aha^{-1}$ (对于 H 中的某个 h $)\}$ 。

证明：

(a) 当且仅当 $s = a^{-1}b s$ 时 as = bs 。

(b) 若 g 在 $aHa^{-1}$ 中，比如 g 在 $aha^{-1}$ ( h 在 H 中) ，则 $(aha^{-1})( as) = ahs = as = s^{'}$ ，因此 g 稳定 $s^{'}$ 。这证明了 $aHa^{-1} \subset H^{'}$ 。由于 $s = a^{-1} s^{'}$ ，我们可以将 s 和 $s^{'}$ 的角色对换，以推导出 $a^{-1}H^{'}a \subset H$ ，这意味着 $H^{'} \subset aHa^{-1}$ 。从而 $H^{'} = aHa^{-1}$ 。

注意：命题的 (b)部分解释了我们在前面数次见到的这种情况：当 $as=s^{'}$ 时，当且仅当 $aga^{-1}$ 固定 $s^{'}$ 时，一个群的元素 g 才固定 s 。

6.8 陪集上的运算(The operation on cosets)

设 H 是群一个群 G 的一个子群。我们知道，左陪集 aH 分割 G 。我们常常将 H 在 G 中的左陪集表示为 G/H ，此符号取自子群为正规群时商群的符号 (2.12.1)；当将陪集 C 视为集合 G/H 的一个元素时，我们使用括号符号 [C] 来表示它。

陪集G/H 之集合不是一个群，除非 H 是一个正规子群。然而，

• 群 G 以一种自然的方式作用于 G/H 。

这个运算相当明显：若 g 是群的一个元素，且 C 是一个陪集，则 g[C] 作用于 [gC] ，其中 gC = { gc | c∈C } 。因此，若 [C ] = [aH] ，则 g[C] = [gaH] 。下一个命题是基础。

命题 6.8.1 令 H 为一个群 G 的子群。

(a) G 在陪集 G/H 上的操作是可传递的。

(b) 陪集 G/H 的稳定器是子群 H 。

再次注意区分：与 H 的元素 h 相乘不会对陪集 H 的元素产生平凡的作用，而是将陪集[H] 映射给自身。

请仔细思考下一个例子。令 G 为具有其常规形式的对称群 $S_{3}$ ，并令 H 为循环子群 {l , y }。其左陪集为

(6.8.2) $C_{1} = H = \{1,y\}$ ， $C_{2} = xH = \{ x,xy \}$ ， $C_{3} = x^{2}H = \{x^{2}, x^{2}y\}$ (见(2.8.4)) ，且 G 作用于陪集 $G/H = \{ [C_{1}] , [C_{2}] , [C_{3}] \}$ 。元素 x 和 y 以相同的方式作用于索引集 {1,2,3} :

(6.8.3) $m_{x} \longleftrightarrow (123)$ 和 $m_{y} \longleftrightarrow (23)$ 。

例如， $yC_{2} = \{ yx , yxy \} = \{ x^{2}y , x^{2} \} = C_{3}$ 。

下一个命题，有时称为轨道稳定器定理，展示了如何用陪集上的运算来描述任意群运算。

命题 6.8.4 令 S 为一个群G 在其上作用的集合，并令 s 为 S 的一个元素。令 H 和 $O_{s}$ 分别表示 s 的稳定器和轨道。则存在一个由 [aH ] ⇝ as 定义的双射 $\epsilon: G/H \rightarrow O_{s}$ 。且对于 每一个陪集 C 和 G 的每一个元素 g，这个映射与群运算 ε(g[C]) = gε([C]) 兼容。

例如，二面体群 $D_{5}$ 作用于一个正五边形的顶点。令 𝒱 表示顶点集，并令 H 表示一个具体顶点的稳定器。则存在一个双射 $D_{5}/H \rightarrow \mathcal{V}$ 。在平面 P的等距 M 的运算中，一个点的轨道是 P 的所有点的集合。原点的稳定器是正交算子的群 $O_{2}$ ，且存在一个双射 $M / O_{2} \rightarrow P$ 。类似地，若 H 表示一条直线的稳定器，而 ℒ 表示平面上的所有直线，则存在一个双向 M / H ⟶ ℒ 。

命题 (6.8.4)之证明：

显然，如果该群存在，则命题表述中定义的映射 ε 将与该群的运算兼容。从符号上讲，ε 只是用符号 s 替换了 H 。不太明确的是，规则 [gH ] ⇝ gs 是否定义了一个映射。由于很多符号 gH 都表示相同的陪集，因此我们必须证明，若 a 和 b 是群元素，且若陪集 aH 和 bH 相等，则 as 和 bs 也相等。假设 aH = bH 。则 $a^{-1}b$ 在 H 中 (2.8.5)。由于H 是 s 的稳定器，因此 $a^{-1} bs = s$ , 从而 as = bs 。因此，我们的定义是合理的，反过来读一下这个推理，我们还会发现，ε 是一个双射。由于 ε 将 [gH ] 带到 gs ，且gs 可以为 $O_{s}$ 的一个任意元素，因此 ε 是满射且单射的。

注意：我们定义映射 ε 时所做的推理经常出现。假设集合 $\overline{S}$ 表示集合 S 上某个等价关系的等价类集合，并令 $\pi :S \rightarrow \overline{S}$ 为将一个元素 s 映射到其等价类 $\overline{S}$ 的一个映射。定义从 $\overline{S}$ 到另一个集合 T 的一个映射 ε 的一种常规方式为：已知 $\overline{S}$ 中的 x ，我们可以选择S 中的一个元素 s ，使得 $x=\overline{s}$ ，并根据 s 来定义 ε(x) 。则我们必须证明(与我们在上所做的一样)，这个定义不依赖于其等价类是x 的 s 的选择，而是仅依赖于 x 。这个过程归结为证明映射是良定义的(well defined)。

6.9 计数公式(The Counting formula)

令 H 为一个有限群 G 的一个子群。我们知道，H 在 G 中的所有陪集都具有相同数量的元素，并且符号 G/H 表示陪集的集合。| G/H | 的阶称为 H 在 G 中的索引[ G:H ] 。则计数公式 (2.8.8) 就成为

(6.9.1) | G| = |H| |G/H| 。

任意群运算的轨道都存在一个类似的公式。

命题 6.9.2 (计数公式) 令 S 为一个群G 在其上作用的有限集，并令 $G_{s}$ 和 $O_{s}$ 分别为 S 的一个元素 s 的稳定器和轨道。则有

$|G| = |G_{s} ||O_{s}|$ 或

(G 的阶) = (稳定器的阶).(轨道的阶)。

可根据(6.9.1)和命题 (6.8.4) 推导。

因此，轨道的阶等于稳定器的索引，即

(6.9.3) $|O_{s}| = |G: G_{s}|$ ，

且轨道的阶分割群的阶。S 的每一个元素 s 都有这样一个公式。

另一个公式使用集合 S 分成的轨道的分割来计算它的元素。我们将按任意分割构成的的 S 的轨道标号为 $O_{1} ,... ,O_{k}$ 。则有

(6.9.4) $| S | = |O_{1}| + ... + |O_{k}|$ 。

公式 (6.9.2) 和 (6.9.4) 都有很多的应用。

例子 6.9.5

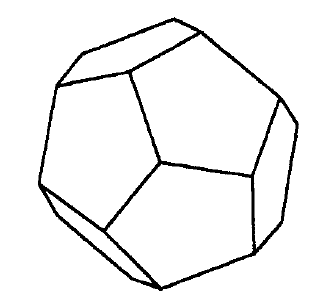
(a) 规则的十二面体(dodecahedron)旋转对称群G 可传递地作用在其面集合 F上。一个特定的面f 的稳定器 $G_{f}$ 是一个绕 f 的中心扫过角度 2π/5的倍数的旋转；其阶为 5 。一个十二面体具有十二个面，因此公式6.9.2 解读为60 = 5.12，因此G的阶数为60。或者，G 传递式地作用于顶点的集合 V 上。一个顶点v 的稳定器 $G_{v}$ 是一个绕这个顶点扫过角度2π/3的倍数的3阶旋转群。一个十二面体具有20个顶点，因此 60 = 3.20，这是可验证的。对于边，也有类似的计算：G 可传递地作用于边的集合，一条边e的稳定器包含幺元和和围绕e的中心扫过角度 π 的旋转。因此 $|G_{e}|=2$ 。由于 60 = 2.30 ，因此一个十二面体有 30 条边。

(b) 我们也可以把群一个群 G 的一个运算限定到一个子群 H 中。通过限定，G 基于集合 S 的一个运算定义了 H 基于 S 的一个运算，并且该运算会导出更多的数值关系。一个元素 s 的 H 轨道将包含在 s 的 G 轨道中，因此单个 G 轨道将分割为多个 H 轨道。

例如，设 F 是十二面体的 12 个面的集合，设 H 是特定面 j 的稳定器，该面是 5 阶循环群。任何 H 轨道的阶数是 1或 5。因此，当我们将 12 个面的集合 F 划分为 H 轨道时，必须找到两个 1 阶轨道。我们这样做：H 固定 j，它固定与 j 相对的面。其余面构成两个 5 阶轨道。公式 6.9.4 表示群 H 在面集上的运算为 12 = 1 + 1 + 5 + 5。或者，令 K 表示顶点的稳定器，该面是 3 阶循环群。我们也可以将集合 F 分割为 K 轨道。在这种情况下，公式 6.9.4 为 12 = 3 + 3 + 3 + 3。

6.10 基于子集的运算(Operations on subsets)

假设一个群 G 作用于一个集合 S 。若 U 是 S 的一个 r 阶子集，则

(6.10.1) gU = { gu | u∈U }

是 S 的另一个 r 阶子集。不难验证一个运算的公理。

例如，令 O 为一个立方体的 24 次旋转的八面体(octahedral)群，并令F 为立方体的六个面的集合。则 O 也同样作用于 F 的2阶子集，即无序的面对(pairs)。一共有 15 个面对，它们构成两条轨道：F = {相对的面对} ∪ {相邻的面对}。这些轨道的阶数分别为 3 阶和 12 阶。

子集 U 的稳定器是群元素 g 的满足[gU] = [U]集合，即，gU = U。一对相对面的稳定器阶为 8 。

再次注意这一点：U 的稳定器由满足 gU = U 的群元素组成。这意味着 g 对 U 内的元素进行置换，即每当 u 在 U 中时， gu 也在 U 中。

6.11 置换表示(Permutation presentations)

在本节中，我们分析一个群 G 可以用于作用于一个集合 S 的各种方式。

• 一个群 G 的置换表示(permutation representations)是一个从群到对称群的同态：

(6.11.1) $\varphi: G \rightarrow S_{n}$ 。

命题 6.11.2 令 G 为一个群。则在 G 的基于 S = {1，…，n} 的运算和置换表示 $G \rightarrow S_{n}$ 之间存在一个双射对应关系：

[G 在 S 上的运算] ⟷ [置换表示] 。

证明：

这很简单，尽管初次看到可能会让人感到困惑。假设给定 G 在 S 上的一个运算，我们定义一个置换表示 φ ，即设 $\varphi_{g}=m_{g}$ (与g 相乘)(6.7.2)。结合律 g(hi) = (gh)i 表明

$m_{g}(m_{h}i) = g(hi) = (gh)i = m_{g}h i$ 。

因此，φ 是一个同态。反之，若 φ 是一个置换表示，则同一公式就定义了G 基于S 的一个运算。

例如，基于一个正 n 边形的顶点 $( v_{1} ,...,v_{n})$ 的二面体群 $D_{n}$ 的运算定义了一个同态 $\varphi:D_{n }\rightarrow S_{n}$ 。

命题 6.11.2 与其适用的索引集没有关系，若 Perm(S) 是任意集合 S 的置换群，此外我们称 φ ：G ⟶ Perm(S) 为 S 的一个置换表示。

推论 6.11.3 令 Perm(S) 表示一个集合 S 的置换群，并令 G 为一个群。则在 G 的基于 S 的运算与 S 的一个置换表示之间存在一个双射对应关系 φ ：G ⟶ Perm(S)：

[G 在 S 上的运算] ⟷ [同态 G ⟶ Perm(S) ] 。

一个置换表示 G ⟶ Perm(S) 不必是单射。若其恰好是单射，则称相应的运算是p忠实的(faithful)。要忠实，运算就必须具有属性： $m_{g}$ (与 g 相乘）不是恒等映射(除非 g = 1 ) ：

(6.11.4) 若一个运算符合后述性质，则称其是忠实的：

对于S 中的每一个 s ，G的满足 gs = s 的唯一元素是幺元。

等距变换群 M 在平面等边三角形集合 S 上的运算是忠实的，因为唯一能将每一个等边三角形都归于自身的等距变换就是恒等变换。

置换表示 G ⟶ Perm(S) 很少是满射的，因为 Perm(S) 的阶趋近于无穷大。但下述例子给出了一种情况。

例子 6.1.5 具有模 2 系数的可逆矩阵的群 $GL_{2}(\mathbb{F}_{2})$ 与对称群 $S_{3}$ 同构。

我们用 F 表示域 $\mathbb{F}_{2}$ ，并且 G 表示群 $GL_{2}(\mathbb{F}_{2})$ 。列向量空间由四个向量组成：

$0=\begin{bmatrix}0\\0 \end{bmatrix}$ , $e_{1}=\begin{bmatrix}1\\0 \end{bmatrix}$ , $e_{2}=\begin{bmatrix}0\\1 \end{bmatrix}$ , $e_{1}+e_{2}=\begin{bmatrix}1\\1 \end{bmatrix}$ 。

群 G 作用于三个非零向量集 $S = \{ e_{1} , e_{2} , e_{1} + e_{2}\}$ ，这给了我们一个置换表示 $\varphi :G \rightarrow S_{3}$ 。幺元是固定 $e_{1}$ 和 $e_{2}$ 的唯一矩阵，因此，基于 S 的G 的运算是忠实的，且 φ 是单射的。一个可逆矩阵的列一定是S 的不同元素的有序对。存在6个这样的对，因此，| G | = 6 。由于 $S_{3}$ 也具有阶 6 ，因此 φ 是一个同构。

6.12 旋转群之有限子群(Finite subgroups of the rotation groups)

在本节中，我们计数公式来分类 $SO_{3}$ 的有限子群 ( $\mathbb{R}^{3}$ 的旋转群)。与平面的等距的有限群一样的情况一样，它们都是我们所熟悉的图形的对称群。

定理 6.12.1 $SO_{3}$ 的一个有限子群是下列群之一：

$C_{k}$ : 围绕一条直线扫过角度 2π/k 倍数的旋转之循环群(k取任意值)；

$D_{k}$ : 一个正 k 边形的对称之二面体群(k 取任意值)；

T : 四面体的 12 个旋转对称四面体群；

O : 立方体或八面体的24个旋转对称的八面体群；

I : 十二面体或二十面体的60个旋转对称的二十面体群。

注意：二面体群通常表示为平面上正多边形的对称群，其中反射的方向相反。然而，平面的反射可以通过在三维空间中旋转角度π来实现，这样，正多边形的对称性就可以实现为 $\mathbb{R}^{3}$ 的旋转。二面体群 $D_{n}$ 可以通过上胆围绕 $e_{1}$ 轴扫过角度 2π/n 的旋转 x 和一个围绕 $e_{2}$ 轴扫过角度 π 的旋转 y 生成。表示这两个旋转的矩阵是(其中，c = cos(2π/n) 而 s = sin(2π/n) )

(6.12.2) $x=\begin{bmatrix} 1&& \\ &c&-s\\ &s&c \end{bmatrix}$ 和 $y=\begin{bmatrix} -1&& \\ &1&\\ &&-1 \end{bmatrix}$ 。

令 G 为 $SO_{3}$ 的一个阶数 N > 1 的有限子群。我们称 G 的一个元素 g ≠ 1 的一个极点(pole)为群的一个极点。 $\mathbb{R}^{3}$ 的除了恒等的任意旋转都有两个极点——旋转由与单位球 $\mathbb{R}^{2}$ 的交集。因此，G 的极点是由不同于 1 的群元素 g 固定的2维球(2-sphere)面上的一个点。

例子 6.12.3 四面体(tetrahedron) Δ 的旋转对称群T 的阶为12。它的极点是位于面心、顶点和边心上方的 $\mathbb{S}^{2}$ 的点。由于Δ 有四个面、四个顶点和六条边，因此有14个极点。

|极点| = 14 = |页数| + |顶点数| + |边数| 。

T 的 11 个元素 g ≠ 1 中的每一个都有两个自旋——两对 (g, p)，其中 p 是 g 的一个极点。因此总共有 22 个自旋。面的稳定器阶数为 3 。它的两个元素 ≠ 1 共用一个位于面中心上方的极点。类似地，有两个元素的极点位于顶点上方，还有一个元素的极点位于边心上方。

|自旋数| = 22 = 2|面数| + 2|顶点数| + |边数| 。

设 𝒫 表示有一个限子群 G 的所有极点的集合。我们可以通过计算这些极点来获取关于该群的信息。如上例所示，计数可能会令人困惑。

引理 6.12.4 G 的所有极点的集合 𝒫 是G 的 轨道的一个并集。因此G基于 𝒫 运算。

证明：

令 p 为一个极点，比如为G中一个元素 g ≠ 1 ，令 h 为 G 的另一个元素，并令 q = hp 。我们必须证明 q 是一个极点，指的是 q 是由 G 的不同于幺元的元素 $g^{'}$ 所固定。则所求的元素是 $hgh^{-1}$ 。这个元素不等于 1 ，因此 g ≠ 1 ，以及 $hgh^{-1}q = hgp = hp = q$ 。

一个极点 p 的稳定器 $G_{p}$ 是 G 中所有围绕 p 的旋转的群。它是一个循环群，由最小正角 θ 的旋转生成。我们用 $r_{p}$ 表示其阶。则 $\theta= 2{\pi}/r_{p}$ 。

由于是一个极点，稳定器 $G_{p}$ 包含一个 1 以外的元素，因此 $r_{p}>1$ 。极点为的 p 的G的元素集是稳定器 $G_{p}$ ，并且忽略幺元。因此，存在 $r_{p}-1$ 个以 p 为极点的群元素。每一个不为 1 的群元素 g 都有两个极点。由于 |G| = |N| ，因此存在 2N – 2 个自旋。这就给出了关系式

(6.12.5) $\sum_{p\in \mathcal{P}}( r_{p-1}) = 2(N - 1)$ 。

我们将某些项聚集在一起以简化公式的左侧：我们令 $n_{p}$ 表示 p 的轨道 $O_{p}$ 的阶。根据计数公式(6.9.2)，我们有

(6.12.6) $r_{p}n_{p} = N$ 。

若两个极点 p 和 $p^{'}$ 位于同一轨道，则它们的轨道是相同的，因此 $n_{p} = n_{p^{'}}$ ，从而 $r_{p} =r_{p^{'}}$ 。我们任意标识各咱轨道，比如标为 $O_{1} , O_{2} ,... , O_{k}$ ，并令 $n_{i}=n_{p}$ 和 $r_{p} = n_{p^{'}}$ ( 对于 $O_{i}$ 中的 p ) , 因此 $n_{i} r_{i} = N$ 。由于轨道 $O_{i}$ 包含 $n_{i}$ 个元素，因此在 (6.12.5)的左边存在 $n_{i}$ 个等于 $r_{i}-1$ 的项。我们把那些项聚集在一起。这样就得出了公式

$\sum_{i=1}^{k}n_{i} (r_{i}-1) = 2N - 2$ 。

我们两边除以 N 就得到了一个著名的公式：

(6.12.7) $\sum_{i}(1-\frac{1}{r_{i}})=2-\frac{2}{N}$ 。

这看起来可能不太像一个许诺的工具，但事实上它释放了很多信息。公式右侧介于1到2之间，而左边的每一项至少是 $\frac{1}{2}$ 。可以推导出，至少存在三个轨道。

余下的分类是通过列举可能情况来完成的：

一个轨道： $1-\frac{1}{r_{1}}=2-\frac{2}{N}$ 。这是不可能的，因此 $1-\frac{1}{r_{1}}<1$ 而 $2-\frac{2}{N} \geq 1$ 。

两个轨道： $\left (1-\frac{1}{r_{1}} \right ) + \left (1-\frac{1}{r_{2}} \right ) =2-\frac{2}{N}$ , 即 $\frac{1}{r_{1}}+\frac{1}{r_{2}}=\frac{2}{N}$ 。

因为 $r_{i}$ 除以 N ，这个公式仅在当 $r_{1} = r_{2} = N$ 的情况下成立，然后有 $n_{1} = n_{2} = 1$ 。

存在两个极点 $p_{1}$ 和 $p_{2}$ ，由群的每一个元素固定。因此，G 是其旋转轴由通过点 $p_{1}$ 和 $p_{2}$ 的直线 𝓁 的旋转的循环群 $C_{N}$ 。

三个轨道： $\left (1-\frac{1}{r_{1}} \right ) + \left (1-\frac{1}{r_{2}} \right ) + \left (1-\frac{1}{r_{3}} \right ) =2-\frac{2}{N}$ 。

这是最有趣的情况，因为 $\frac{2}{N}$ 是正的，此公式表明

(6.12.8) $\frac{1}{r_{1}}+\frac{1}{r_{2}}+\frac{1}{r_{3}}=\frac{2}{N}$ 。

我们按递增的次序重排 $r_{i}$ 。则 $r_{1}=2$ ：若所有 $r_{i}$ 至少为 3，就上式左边就会 ≤ 1 。

第1种情况： $r_{1} = r_{2} = 2$ 。第三阶 $r_{3} = k$ 可以是任意的，且 N = 2k : $r_{i} = 2 , 2 , k ; n_i = k , k , 2; N = 2k$ 。

存在一个构成轨道 $O_{3}$ 的极点对 $\{ p , p^{' }\}$ 。G的一半元素固定p ，另一半元素交换 p 和 $p^{'}$ 。因此 G 的元素是围绕经过 p 和 $p^{'}$ 的直线 𝓁 的旋转，或是围绕垂直于 𝓁 的直线扫过角度 π的旋转。因此，群 G 是固定了一个正 k 边形 Δ 的旋转群，即二面体群 $D_{k}$ 。多面体 Δ 位于垂直于 𝓁 的平面中，且 Δ 的顶点和面心对应于余下的极点。Δ 在 $\mathbb{R}^{2}$ 中的双面对称性已知成为 $\mathbb{R}^{3}$ 中绕过角度 π 的旋转。

第2种情况： $r_{1} = 2$ 和 $2 < r_{2} \leq 3$ 。等式 1/2 + 1/4 + 1/4 = 1 排除了 $r_{2} \geq 4$ 的可能性。因此 $r_{2}=3$ 。然后，等式 1/2 + 1/3 + 1/6 = 1 排除了 $r_{3} \geq 6$ 的可能性。只剩下三种可能性：

(i) $r_{i} = 2, 3, 3 ; n_{i} = 6, 4, 4 ; N = 12$ 。

轨道 $O_{3}$ 中的极点是正四面体的顶点，G 是其 12 个旋转对称的四面体群 T 。

(ii) $r_{i} = 2, 3, 4 ; n_{i} = 12, 6, 6 ; N = 24$ 。

轨道 $O_{3}$ 中的极点是正八面体的顶点，G 是其 24 个旋转对称的八面体群 O 。

(iii) $r_{i} = 2, 3, 5 ; n_{i} = 30, 20, 12 ; N = 60$ 。

轨道 $O_{3}$ 中的极点是正二十面体的顶点，G 是其 60 个旋转对称的二十面体群 I 。

在每一种情况下，整数 $n_{i}$ 分别是边数、面数和顶点数。

直观地讲，轨道上的极点应该是正多面体的顶点，因为它们在球面上必须等距分布。然而，这并不完全正确，因为，例如，立方体的边心虽然构成轨道，但它们并不跨越正多面体。它们所跨越的图形称为截角多面体(a truncated polyhedron)。

我们将验证断言 (iii) 。令 V 为 12阶的轨道 $O_{3}$ 。我们希望证明这个轨道中的极点是一个正二十面体(a regular icosahedron)的顶点。令 p 为 V 中的极点之一。将 p 视为单位球的北极点就给到了我们一个赤道(equator)和一个南极点。令 H 为 p 的稳定器，由于 $r_{3}=5$ ，则此稳定器是一个循环群，由绕 p 扫过角度 2π/5 的旋转生成。当我们将 V分解成 H 轨道的时候，我们至少会获得两个1阶H轨道。它们分别是北极和南极。组成 V 的另外10个轨道构成了两个五阶 H 轨道。我们将其分别记为 $\{ q_{0} ,..., q_{4} \}$ 和 $\{ q_{0}^{'} ,... , q_{4}^{'} \}$ ，其中 $q_{i} = x_{i} q_{0}$ 以及 $q_{i}^{'} = x_{i} q_{0}^{'}$ 。根据南北极的对称性，这些H轨道一个位于北半球(hemisphere)，一个位于南半球，或者两个轨道都位于赤道。我们假设轨道 $\{q_{i}\}$ 位于北半球或赤道。

令 |x , y | 表示单位球上点 x 和 y 之间的球面距离。我们注意到， $d = |p, q_{i}|$ 与 i = 0,…,4 无关。当为，当固定 p 的时候，存在 H 的一个元素，其搬运 $q_{0} \rightsquigarrow q_{i}$ 。类似地， $d^{'} = |p, q_{i}^{'} |$ 与 i 无关。因此，由于 $p^{'}$ 覆盖轨道 V ，距离 $| p,p^{'}|$ 仅在4个值 0 ，d , $d^{'}$ 和 π 上取值。值 d 和 $d^{'}$ 的值各取五次，0 和 π 取一次。由于 G 对 V 具有传递性，因此当 p 被 V 中的任何其他极点替换时，我们都会得到相同的四个值。

我们注意到，当 $d^{'} \geq \pi/2$ 时，d ≤ π/2 。因为在轨道 $\{q_{i}\}$ 中存在 5 个极点，球面距离 $|q_{i} , q_{i+1}|$ 小于 π/2 ，因此其等于 d ，且小于 π/2 。从而轨道不在赤道上，这三个极点 p , $q_{i}$ , $q_{i+1}$ 构成了一个等边三角形。有5个相交于p点的全等等边三角形。因此，在每一个极点处有五个全等三角形相交。它们构成了二十面体的面。

注意：正多面体只有五种。这可以通过计算将全等的正多边形在顶点处拼接在一起，从而以构建正多面体的方法数量来开始证明。我们可以拼凑三个、四个或五个等边三角形，三个正方形，或三个正五边形。(六个三角形、四个正方形或三个六边形可以粘合成平面。)所以只有五种可能性。但这种分析忽略了一个有趣的问题：二十面体存在吗？当然，我们可以用纸板做一个。但即使我们这样做，三角形也永远无法精确地拼接在一起，我们就轻易地认为这是因为我们不够精确。如果我们对音乐中的五度圈得出类似的结论，那就错了：五度圈几乎闭合，但并不完全闭合。确定二十面体存在的最佳方法可能是写下它的顶点坐标并检查距离。见习题 12.7。

我们对平面等距的讨论与三维空间等距群类似。我们可以定义晶体群的概念，它是一个离散子群，其平移群是三维晶格。晶体群类似于二维晶格群，而晶体是具有对称性等群的三维构形的例子。可以证明，晶体群有230种类型，类似于17个晶格群(6.6.2)。这个列表太长，不实用，因此晶体被更粗略地分为七个晶系。有关更多信息，以及对32个晶体点群的讨论，请参阅晶体学(crystallography)方面的书籍，例如[Schwarzenbach]。

Un bon héritage vaut mieux que Ie plus joli problème de géométrie, parce qu'il tient lieu de méthode générale, et sert à resoudre bien des problèmes.

(好的继承比最漂亮的几何问题更有价值，因为它是一种通用方法，可以用来解决很多问题。)

--------------------------------------------Gottfried Wilhelm Leibnitz

(注：我从V.l. Arnold. 那里学到了这句话。l’Hôspital曾写信给Leibnitz，为长时间的沉默道歉，并说他一直在乡下处理一笔遗产。Leibnitz在回信中告诉他不用担心，并继续引用了那句话。)

内容来源：

<<Algebra>> Michael Artin, 2th

查看全文

http://www.dtcms.com/a/317667.html