机器学习——贝叶斯
一·贝叶斯算法 - 定理相关
贝叶斯算法
贝叶斯定理:
条件概率
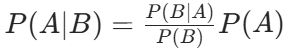
解决问题:逆概问题
二·贝叶斯算法 - 概率类型示例
贝叶斯算法 正向概率: 假设袋子里有 10 个白球,90 个黑球,然后从袋子里面拿出一个球,拿出的球是白球的概率是多少?
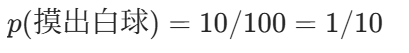
逆向概率:
如果我们事先并不知道袋子里白球、黑球的比例,然后通过多次试验,根据拿出来球的颜色推测袋子里白球、黑球的比例。
三·贝叶斯算法 - 推导及实例(学校学生场景)
贝叶斯算法
推导贝叶斯:
在一个学校里面,男生占 60%,女生占 40%;
男生:100% 穿长裤,女生:50% 穿长裤,50% 穿裙子;
此时迎面走来一个穿长裤的学生,刚好你是高度近视,那么要判断一下这个穿长裤的学生是女生的概率该怎么计算?
实质:
穿长裤的是女生的概率 = 女生中穿长裤的人数 / 穿长裤的总人数
贝叶斯算法
假设:
全校人数(U):1000 人。
男生中穿长裤的人数:
![]()
女生中穿长裤的人数:
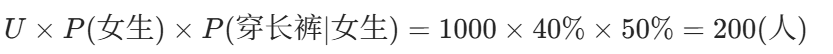
四·穿长裤且是女生的概率:
(200 / (200 + 600) = 25%
实质:
穿长裤的是女生的概率 = 女生中穿长裤的人数 / 穿长裤的总人数
定义:
A— 男生 B— 女生 C— 穿长裤
贝叶斯算法
Eg1:
已知在所有男子中有 5% 患色盲,在所有女子中有 0.25% 患色盲,随机抽一个人是色盲,其为男子的概率是多大?(假设男子与女子人数相等)
A: 抽到男子 B: 抽到女子 C: 抽到色盲
五、朴素贝叶斯分类器应用(数据集分类预测)
| 步骤 | 内容 |
|---|---|
| 数据集情况 | 含 3 个特征(A、B、C )和 1 个类别标签(D )的数据集,示例数据如下: 特征 A:1、0、0、1、1、0 特征 B:0、1、1、0、0、1 特征 C:1、1、0、0、0、1 类别 D:0、1、0、1、0、1 |
| 目标 | 用朴素贝叶斯分类器预测新样本(如特征 A=1,特征 B=1,特征 C=0 )的类别 |
| 核心逻辑 | 把输入当条件,算结果为 0 和 1 的概率,选概率大的类别 |
| 计算步骤 1:先验概率 | \(P(D=0) = 3/6 = 0.5\);\(P(D=1) = 3/6 = 0.5\)(类别 0、1 在数据集中出现频率 ) |
| 计算步骤 2:特征条件概率(部分示例 ) | \(P(A=1|D=0) = 2/3 ≈ 0.667\);\(P(B=1|D=0) = 1/3 ≈ 0.333\);\(P(C=0|D=0) = 2/3 ≈ 0.667\) \(P(A=1|D=1) = 1/3 ≈ 0.333\);\(P(B=1|D=1) = 2/3 ≈ 0.667\);\(P(C=0|D=1) = 1/3 ≈ 0.333\)(特征在各类别下出现的条件概率 ) |
| 计算步骤 3:后验概率(以新样本 A=1,B=1,C=0 为例 ) | \(P(D=0|A=1,B=1,C=0) = P(D=0)×P(A=1|D=0)×P(B=1|D=0)×P(C=0|D=0) ≈ 0.5×0.667×0.333×0.667 ≈ 0.083\) \(P(D=1|A=1,B=1,C=0) = P(D=1)×P(A=1|D=1)×P(B=1|D=1)×P(C=0|D=1) ≈ 0.5×0.333×0.667×0.333 ≈ 0.037\)(新样本属于各类别的概率 ) |
| 预测结果 | 选后验概率大的类别,即 \(D = 0\) |
六、代码工具及参数(sklearn.naive_bayes.MultinomialNB )
| 标题 | 内容 |
|---|---|
| 代码类 | sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None) |
参数 1:MultinomialNB | 多项式分布的朴素贝叶斯 |
参数 2:alpha | 控制模型拟合时的平滑度,是添加剂(拉普拉斯 / Lidstone)平滑参数,控制概率估计平滑程度;平滑用于防止过拟合,尤其处理稀疏数据集或训练集未出现特征时。\(\alpha = 0\) 时不平滑,\(\alpha = 1\) 时为拉普拉斯平滑,\(0<\alpha<1\) 时为 Lidstone 平滑 |
七·代码
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score, classification_reportdigits = load_digits()
X = digits.data
y = digits.targetX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42
)model = GaussianNB()model.fit(X_train, y_train)y_pred = model.predict(X_test)accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.4f}")
print("\n分类报告:")
print(classification_report(y_test, y_pred))