向量范数与矩阵范数

  在实数空间R中，可以很方便比较两个数的大小关系。而针对两个n维向量  

，

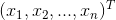
，如果需要比较大小关系，需要定义一个准则，如到原点距离（即欧氏距离）。而范数即为不同的准则，如 

 等，其公式为：

。

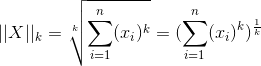
    当k=2时，即为常见的欧式距离；当k=1时，为向量中各元素绝对值之和；当k=0时，表示向量中非零元素个数；当 

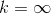
 时，表示向量中绝对值最大元素绝对值。

   针对 

 时，可以使用极限求解，有 

。

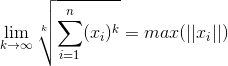
   将矩阵作用于向量（矩阵左乘向量），表示矩阵对向量进行线性变换。如果矩阵为单位矩阵，则变换后向量于变换前保持一致。如果矩阵非单位向量，变换后向量与变换前则存在差异，不同矩阵对向量的变换的差异不一致，这里使用矩阵范数表示这种变换的最大差异。显然，要度量变换前后向量差异，需要选择合适的度量准则，即以上所述的向量范数。

   在选择了合适的向量范数后，对应的矩阵范数表示该度量规则下矩阵变换前后的最大差异，则有：

   1）使用矩阵每列绝对值之和的最大值表示矩阵A的 

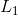
 范数；

   2）使用矩阵每行绝对值之和的最大值表示矩阵A的 

 范数；

   3）使用 

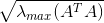
 （矩阵 

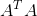
 最大特征值开平方）表示矩阵A的 

 范数。