调试|谷歌浏览器调试长连接|调试SSE和websocket
长连接需求不常有,控制台调试的细节容易忘,在这截图备忘。本文会记录SSE、websocket连接、普通接口 在谷歌浏览器控制台的对比
文章目录
- SSE(Server-Sent Events)
- 观察对象:百度翻译
- 观察请求头和响应头
- 观察EventStream
- 观察response
- Websocket
- 观察对象:随便找一个在线websocket测试网站
- 观察请求头响应体
- 观察Messages
- 非长连接接口
SSE(Server-Sent Events)
观察对象:百度翻译
通过百度翻译接口观察sse响应,控制台会出现EventStream模块。由于接口名是translate,所以可以通过translate关键字筛选出特定接口。且,sse接口能在Fetch/XHR分类下找到
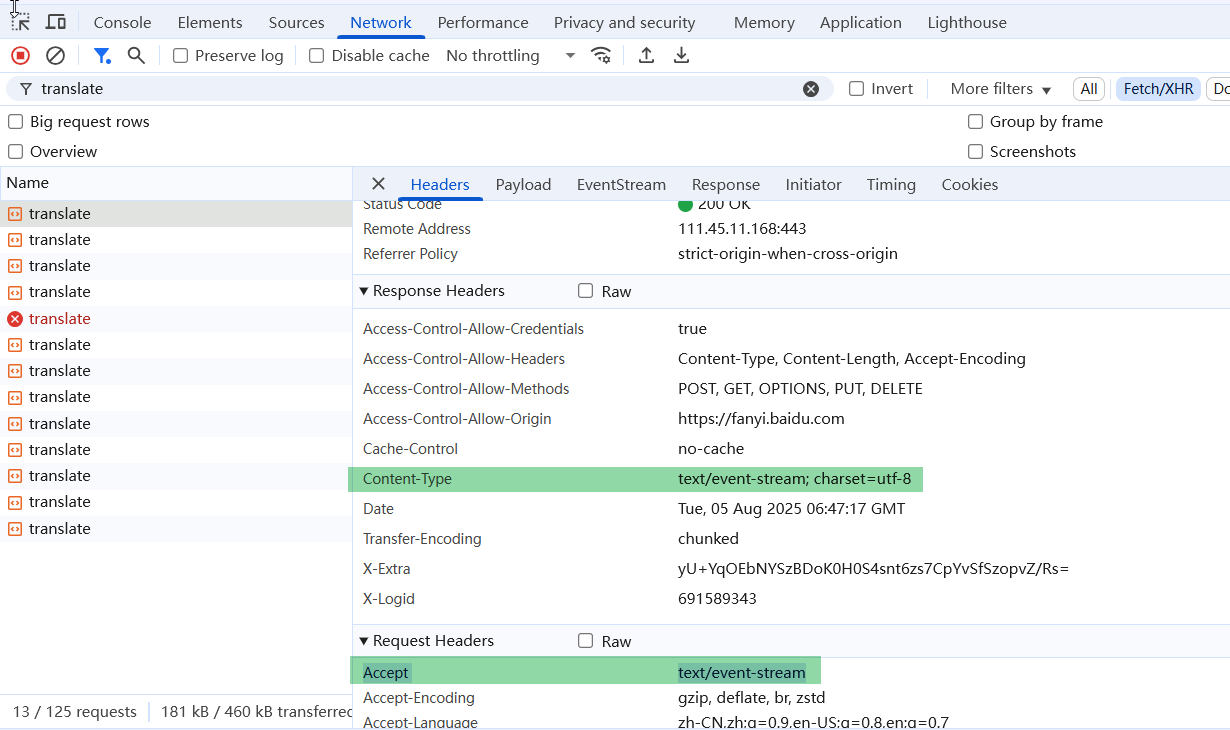
观察请求头和响应头
请求头和响应头重都带上text/event-stream,通常表示客户端和服务器之间正在协商使用 Server-Sent Events (SSE) 协议进行通信。通常流式传输的响应头也会带上Transfer-Encoding: chunked,这是 HTTP 协议中的一种传输编码方式,它允许服务器在不知道内容总长度的情况下,逐步发送数据给客户端
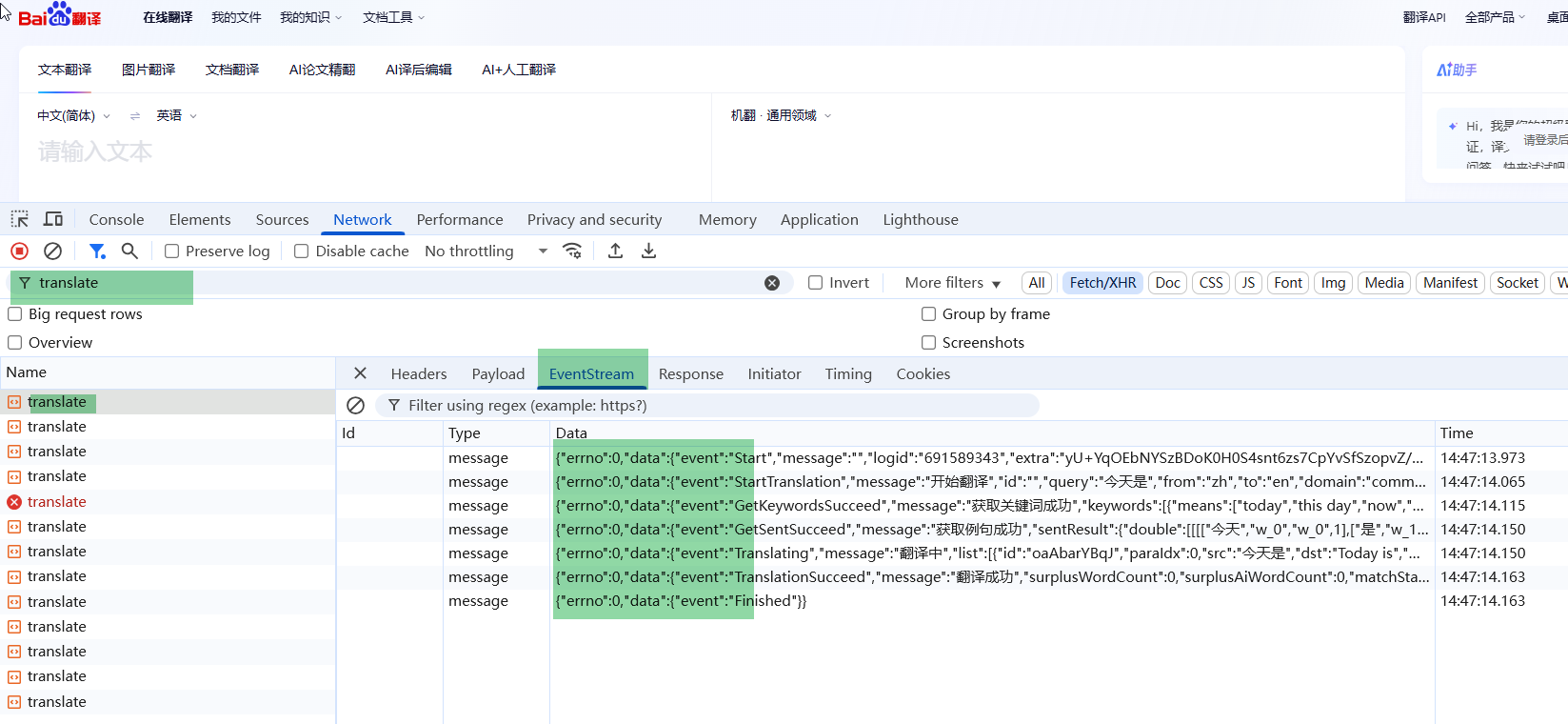
观察EventStream
数据格式:每条消息以 data: 开头,用两个换行符 \n\n 分隔
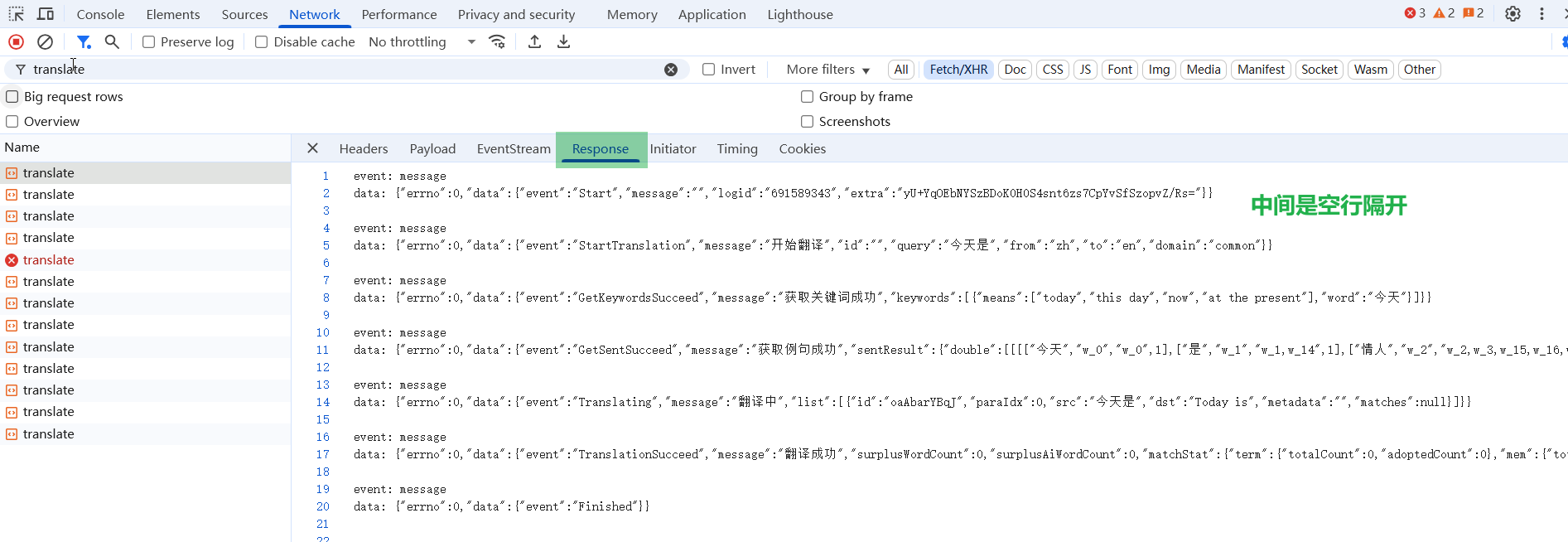
观察response
可以看到数据格式:每条消息以 data: 开头,用两个换行符 \n\n 分隔
Websocket
观察对象:随便找一个在线websocket测试网站
此处观察网站用的是:http://tool.chacuo.net/websocket
截图中,websocket接口在Socket模块下,不在Fetch/XHR
观察请求头响应体
注意观察特有字段
请求头
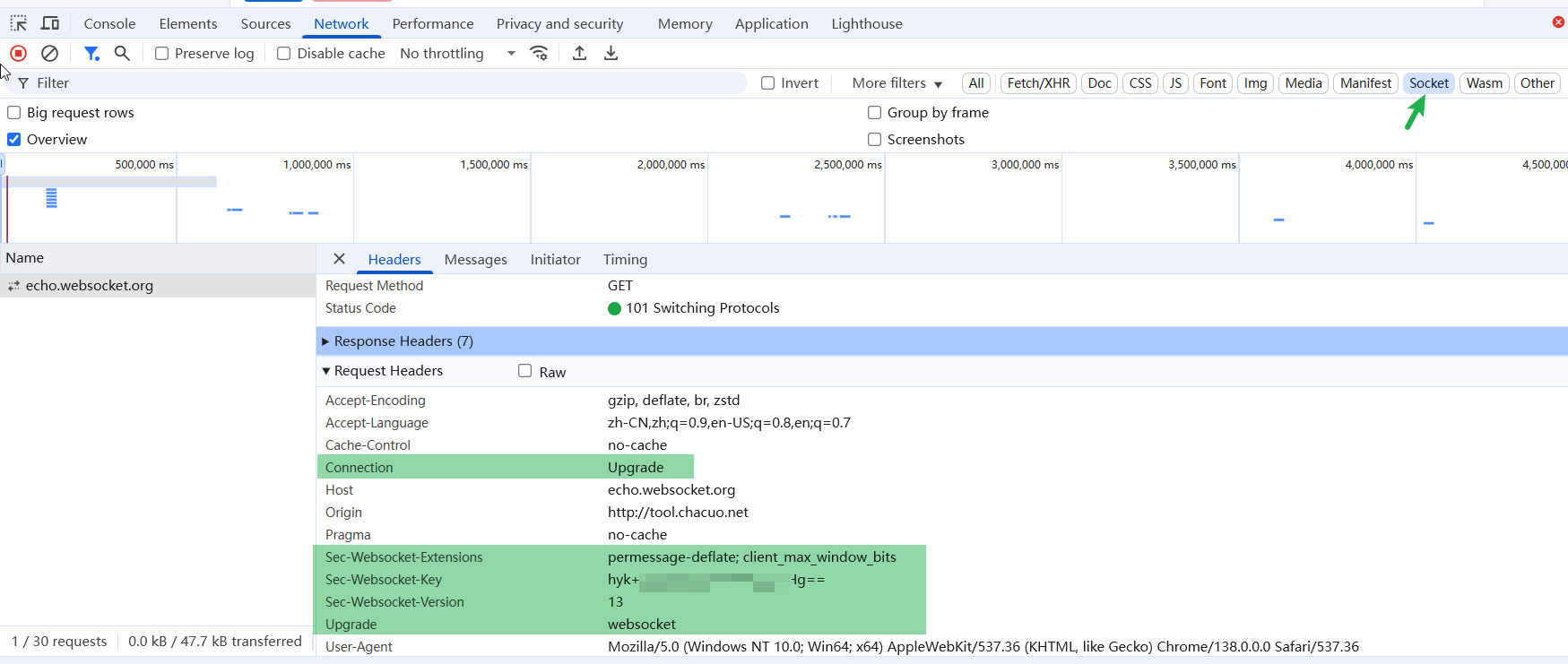 响应头
响应头
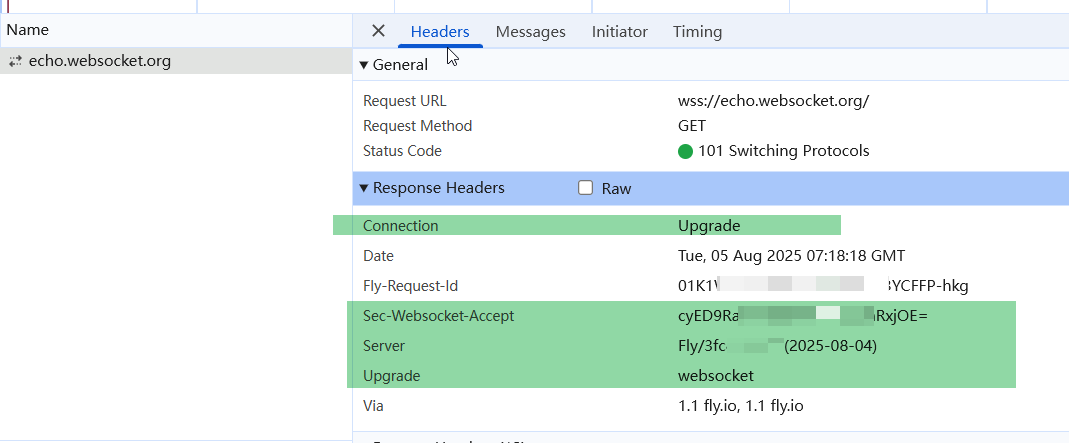
字段说明
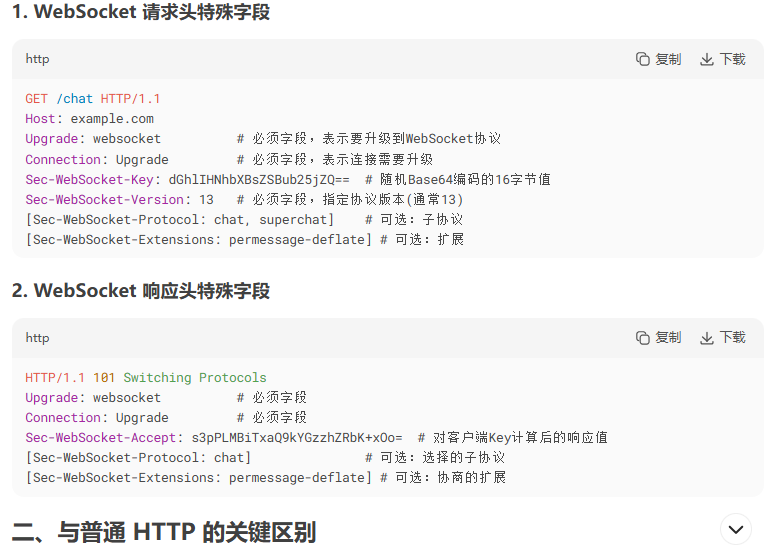
观察Messages
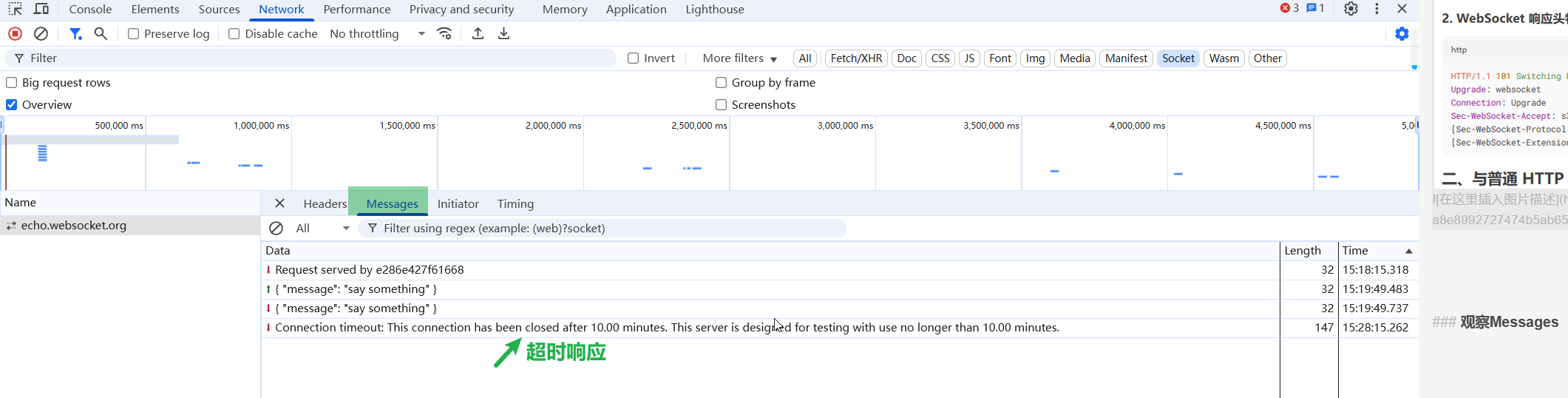 控制台支持筛选发送方或响应方消息
控制台支持筛选发送方或响应方消息

非长连接接口
对于一个非长连接接口(或者说一个普通的接口),控制台通常只显示以下信息,不会出现EventStream或者Messages