当前位置：首页 > news >正文

数据结构与算法：哈希函数的应用及一些工程算法

news 2025/8/5 9:37:18

前言

这篇里的东西可以说了解了解就行了。

一、哈希函数均匀性展示

原本让deepseek转了一下老师的java代码，但发现复刻起来太麻烦了。又因为这个理解就好，竞赛不会有，所以就直接贴老师的java代码了……

import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;
import java.security.Security;
import java.nio.charset.StandardCharsets;
import java.math.BigInteger;
import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;public class hash {// 哈希函数实例public static class Hash {private MessageDigest md;// 打印支持哪些哈希算法public static void showAlgorithms() {for (String algorithm : Security.getAlgorithms("MessageDigest")) {System.out.println(algorithm);}}// 用具体算法名字构造实例public Hash(String algorithm) {try {md = MessageDigest.getInstance(algorithm);} catch (NoSuchAlgorithmException e) {e.printStackTrace();}}// 输入字符串返回哈希值public String hashValue(String input) {byte[] hashInBytes = md.digest(input.getBytes(StandardCharsets.UTF_8));BigInteger bigInt = new BigInteger(1, hashInBytes);String hashText = bigInt.toString(16);return hashText;}}public static List<String> generateStrings(char[] arr, int n) {char[] path = new char[n];List<String> ans = new ArrayList<>();f(arr, 0, n, path, ans);return ans;}public static void f(char[] arr, int i, int n, char[] path, List<String> ans) {if (i == n) {ans.add(String.valueOf(path));} else {for (char cha : arr) {path[i] = cha;f(arr, i + 1, n, path, ans);}}}public static void main(String[] args) {System.out.println("支持的哈希算法 : ");Hash.showAlgorithms();System.out.println();String algorithm = "MD5";Hash hash = new Hash(algorithm);String str1 = "zuochengyunzuochengyunzuochengyun1";String str2 = "zuochengyunzuochengyunzuochengyun2";String str3 = "zuochengyunzuochengyunzuochengyun3";String str4 = "zuochengyunzuochengyunZuochengyun1";String str5 = "zuochengyunzuoChengyunzuochengyun2";String str6 = "zuochengyunzuochengyunzuochengyUn3";String str7 = "zuochengyunzuochengyunzuochengyun1";System.out.println("7个字符串得到的哈希值 : ");System.out.println(hash.hashValue(str1));System.out.println(hash.hashValue(str2));System.out.println(hash.hashValue(str3));System.out.println(hash.hashValue(str4));System.out.println(hash.hashValue(str5));System.out.println(hash.hashValue(str6));System.out.println(hash.hashValue(str7));System.out.println();char[] arr = { 'a', 'b' };int n = 20;System.out.println("生成长度为n，字符来自arr，所有可能的字符串");List<String> strs = generateStrings(arr, n);
//		for (String str : strs) {
//			System.out.println(str);
//		}System.out.println("不同字符串的数量 : " + strs.size());HashSet<String> set = new HashSet<>();for (String str : strs) {set.add(hash.hashValue(str));}
//		for (String str : set) {
//			System.out.println(str);
//		}System.out.println("不同哈希值的数量 : " + strs.size());System.out.println();int m = 13;int[] cnts = new int[m];System.out.println("现在看看这些哈希值，% " + m + " 之后的余数分布情况");BigInteger mod = new BigInteger(String.valueOf(m));for (String hashCode : set) {BigInteger bigInt = new BigInteger(hashCode, 16);int ans = bigInt.mod(mod).intValue();cnts[ans]++;}for (int i = 0; i < m; i++) {System.out.println("余数 " + i + " 出现了 " + cnts[i] + " 次");}}}

直接cv的，咱也不研究写法，直接看结果吧。

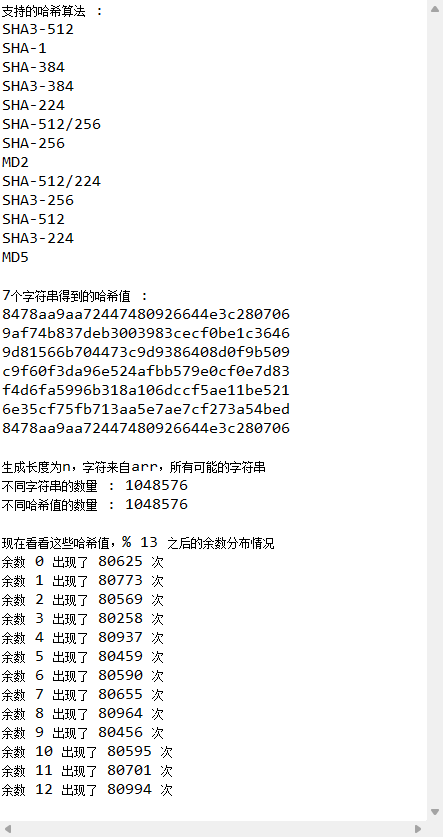
可以发现，虽然那几个字符串相似度很高，但映射出来的哈希值差别非常大，这就完美体现了哈希函数的均匀性。同时，第一个字符串和最后一个字符串完全一样，所以第一个和最后一个的哈希值也完全一样。

接着，生成大量相似的字符串后，将其存到set里，可以发现数量能对得上，说明没有发生哈希碰撞。之后再将所有的哈希值模13分组，可以发现每个结果的出现次数非常相近，这也能体现哈希函数的均匀性。

二、利用均匀性解决问题

问题描述：

一台机器上硬盘空间很大，但内存空间很少，只有4G。给定100亿个字符串的文件，每行是一个长100字节的字符串，统计哪个字符串出现次数最多。

问题解决：

这个第一眼就是用个map存个数，但再分析可以想到，如果字符串相同的话，进map其实只会增加对应的值，这是不太占用内存的。但如果最差情况下，即所有字符串都不同，那么map就需要开100亿个键去存，这就会占用大量的空间了，估算一下是1T。

反推一下，假设4G的内存都用来存，那么map最多可以存3700万个键，再保守一下当成1000万个。之后先用100亿除以这1000万得到1000，那就可以在读取每条字符串时先用哈希函数计算其哈希值。接着再把这个哈希值模上1000分组，然后把这条字符串分到其余数对应的文件里。因为哈希函数的特性，相同的字符串不可能分到两个文件里。此时，虽然从个数上说，1000个文件里的数量不一定相同，但种类一定是均匀的。那么最后只需要关于每个文件用map统计最大词频的字符串，再统计这1000个文件的最大词频即可。

其实，很多工程上的问题都是利用哈希函数把大量的数据均匀分散到多个组里分别解决的。

三、哈希表原理

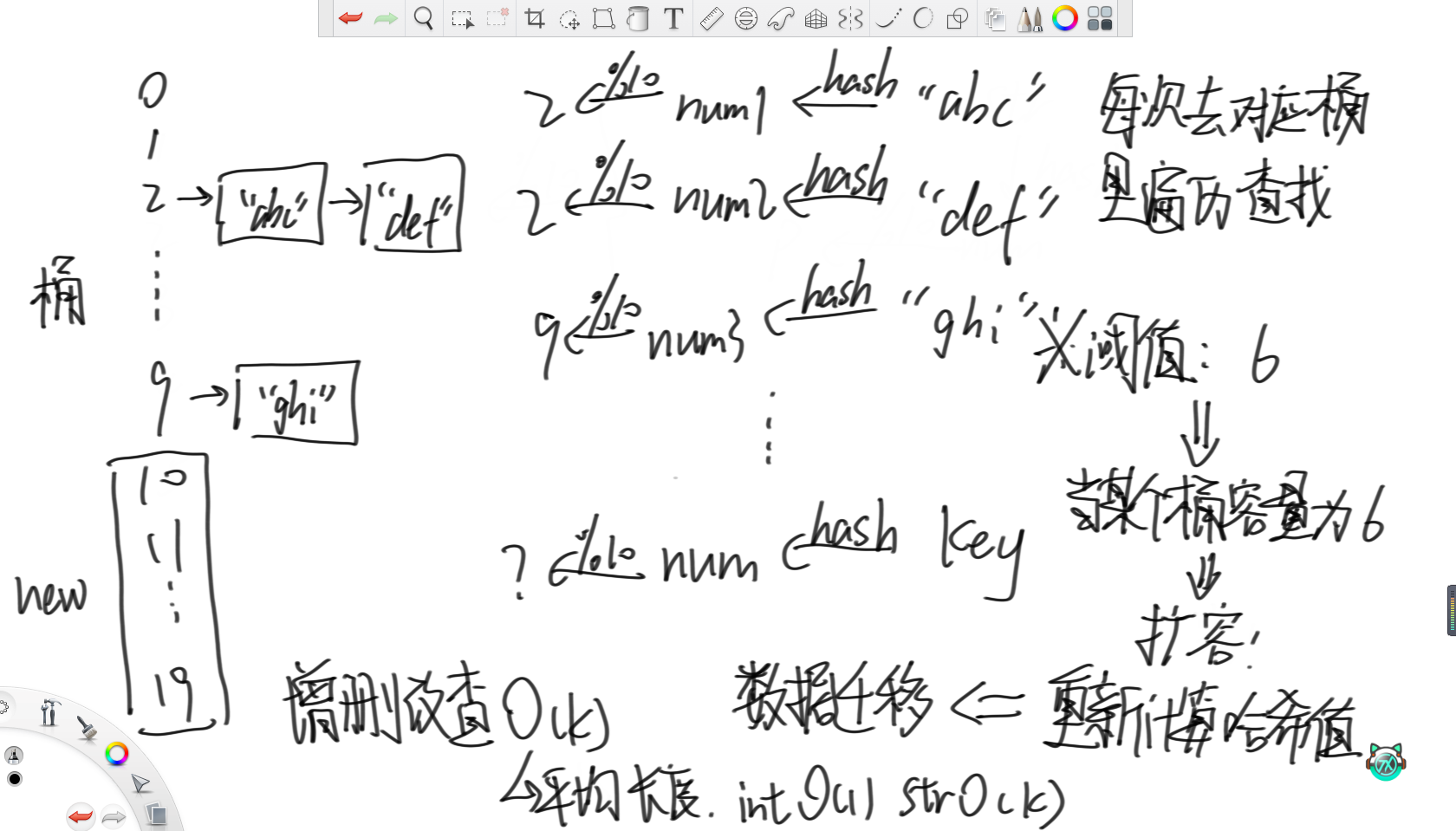
哈希表利用的就是上面写的哈希函数的均匀性。首先，哈希表会初始准备若干个桶，这里假设10个。之后对于每一个要存入的字符串，都先用哈希函数计算出一个数值，然后模上桶的个数对其进行分组，再根据分好的组将其放入对应的桶里。那么如果要查某一个字符串的话，就可以先计算出其哈希值并取模，然后去对应的桶里遍历查找即可。

因为哈希函数的均匀性，所以各个桶里的字符串数量应该是差不多的。所以当某个桶里字符串的个数达到了某个阈值，那么就可以认为所有桶里的个数都接近了这个阈值。此时就认为每次遍历查找的代价过高，所以就考虑增加桶的数量，这里选择将桶的个数翻倍。然后重新计算之前所有入桶的字符串的哈希值并重新分组，这称为“数据迁移”。

所以，哈希表增删改查的时间复杂度为O(k)，若存储的是数字，那么时间复杂度就是O(1)，若是字符串，那么时间复杂度就是O(k)，其中k为字符串的平均长度。

不难看出，可以通过设置哈希表的初始桶数、阈值、扩容因子、哈希函数和桶的结构来提高哈希表的性能。其中，扩容因子就是一次增加的桶的个数，桶的结构可以用数组实现、链表实现或者更高级的红黑树实现。

四、布隆过滤器

布隆过滤器可以理解为一个黑名单系统。其特点是可以保证在这个黑名单系统里的对象会被完全排除掉，但缺点是有可能排除不在黑名单里的对象。

首先，布隆过滤器需要准备一个位图。位图虽然本质上就是一个整型变量，但其十进制数字不代表任何含义，是用其32个二进制位来表示对应位的数字存在或不存在。之后，对于每个要进入这个布隆过滤器的id，用k个哈希函数将其转化成数字，再将这几个数字模上位图的长度m，然后在位图上将这几个数字对应的位置全部涂黑即可。每当有一个id到来时，就用同样的方法计算出其在位图上的对应位置，若全是黑的就说明需要被排除掉。

所以根据哈希函数必然存在哈希碰撞的原理，布隆过滤器一定存在误报的情况。那么就能得出，位图长度越大，失误率就越低。而随着哈希函数的个数k的增大，失误率会先下降，达到最低后会上升，因为会快速占满整个位图。

五、一致性哈希

1.经典存储结构

在讲述一致性哈希前，先讲一下经典的存储结构。

假设有三个机器用来存储，对于每一个要存储的key，都通过哈希函数转化成一个数值，然后对其模3分组，存到对应的机器里。但很明显，这种存储结构存在两个问题。

首先就是当传来的key的数量不是很多，且对其查询的频率存在高低差异时，会导致机器的负载不均衡。举个例子，对于所有国家名称的词条，肯定“中国”和“美国”的搜索频率远高于其他国家，甚至可能高于其他国家的总和。这时，假如这俩词条被分到同一个机器里，那么这个机器的负载必然远大于其他两个机器。

第二个问题就是，假如到了节假日，搜索的频率大大增加时，此时肯定需要通过增加机器来维持运营。那么就需要把里面存在的所有词条都拿出来重新计算哈希值分组，这样数据迁移的代价就非常大了。

2、一致性哈希

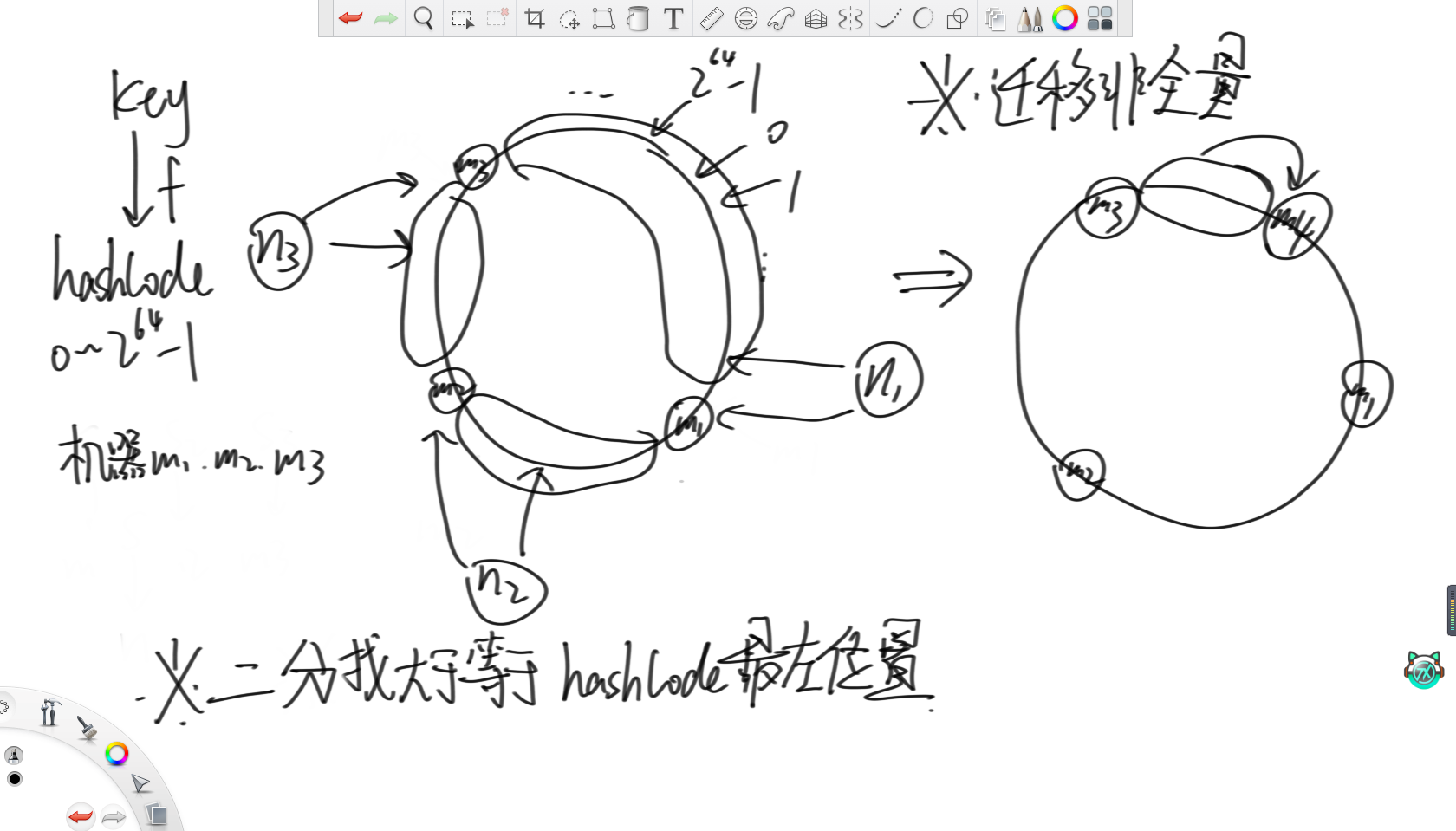
一致性哈希就是将哈希值的范围0~2的64次方-1看成一个环，然后先用哈希值将三台机器的id转化出一个哈希值，然后打到这个环上的三个点。之后，对于每个到来的key，在计算出其哈希值后，让它们也打到环上。然后根据这三个机器在环上的位置将环分为三组，每个机器负责打在自己组里的key，那么体现到代码上就是每次在所有机器的哈希值里二分找大于等于key的哈希值的最左位置即可。这样，当要增加机器时，只需要对部分数据进行迁移即可，此时数据迁移的代价就不是全量的了。

3.一致性哈希的缺陷

观察这个过程不难发现，一致性哈希也存在一个缺陷，那就是依然无法解决负载不均的问题。当这几个机器id的哈希值打在环上的位置无法把环等分，那么依然会存在一台机器负责大多数key的情况。

4.改进方法——虚拟节点技术

基于这个问题，就出现了虚拟节点技术。虚拟节点技术说的是，既然原本因为机器数较少，不能很好地体现哈希函数的均匀性，从而导致负载不均，那么现在考虑对每个机器都增设虚拟节点。在上图例子中，就对分别三台机器增加了1000个虚拟节点，然后让这3000个虚拟节点去抢环，这样3000个点就比3个点更能体现哈希函数的均匀性，就能实现三台机器负载均衡。之后，再按照上述分配key的方法分配到对应的虚拟节点上，再由虚拟节点映射到机器上即可。

当需要增加或减少节点数，就可以再来1000个虚拟节点，那么迁移的代价依然不是全量的。而对于性能有差异的机器，可以让性能好的机器负载更多的key，那么就可以通过设置每台机器虚拟节点数，让高性能的机器多分节点，从而实现合理管理机器的负载。

六、一些有趣的工程算法

1.蓄水池采样

假设有一个不停吐出球的机器，每次吐出1号球、2号球、3号球……有一个袋子只能装下10个球，每次机器吐出的球，要么放入袋子，要么永远扔掉。如何做到机器吐出每一个球后，所有吐出的球都等概率地被放进袋子。

这个题的思路就很巧妙了。

对于前m个球，那没啥好说的，直接放入袋子。之后，每次对于第i号球，都以m/i的概率决定要还是不要。如果要的话，那么就需要等概率地淘汰袋子中的某个球。

在上述例子中，假设m等于10，那么当第11号球来到时，那么要的概率就是10/11。对于第12号球，要的概率就是10/12。

所以，对于第3号球，当吐出第11号球时，这颗球被淘汰的概率就是11号球要，且选中3号球淘汰的概率，那么就是1/10乘以10/11，等于1/11，所以3号球留下的概率就是10/11。同理，当吐出12号球时，3号球留下的概率为11/12。所以3号球最终留下的概率就是所有留下的概率相乘，那么约分完就等于10/n。由此可得所有球留下的概率均相等。

拓展问题：如何设计一个抽奖系统，让一天内所有首次登录的用户都有均等的抽奖机会，中奖人数一共100人。

这个问题就和蓄水池采样很类似了，就是让前一百个人直接选中，之后每来一个人都按100/i的概率决定要还是不要即可。

2.内存限制类问题

32位无符号整数的范围是0~4,294,967,295，现在有一个正好包含40亿个无符号整数的文件。可以使用最多1G的内存，如何找到出现次数最多的数。

这个跟前面利用哈希函数均匀性的题一样，重点是在这个情境下延伸出的其他问题。

（1）内存只有1G，如何找到所有没出现过的数字。

内存只有1G，那么肯定不可能开个数组记录出没出现过，又因为只需要判断出没出现过，所以就考虑使用位图表示一个数是否出现过即可。

（2）内存只有1G，如何找到所有出现了两次的数

因为要找到所有出现两次的数，既然同样不能直接开个数组，那么同样考虑使用位图，但现在不用一位表示出没出现过，而是用两位表示一个数表示这个数出现几次。那么00就是没出现过，01就是出现一次，10就是出现两次，11出现三次，大于三的情况直接不改了即可。最后只需要统计有几个10状态即可。

（3）内存只有3KB，如何只找到一个没出现过的数

首先，3KB大约相当于3000位，大约就是750个int，而最接近750的2的幂是512。所以考虑将一个无符号int能表示的范围分为512组，所以一组里就有2的32次方除以512，即8388608个数。然后用512个int变量，表示范围内数字的出现次数。在上面例子中，a变量就负责统计0~8388607范围上的数字的词频。那么对于缺失的数字，词频必然不够8388608个，那么就再将这个范围分为512组继续统计词频即可。

（4）内存只有几个变量的空间，如何只找到一个没出现过的数

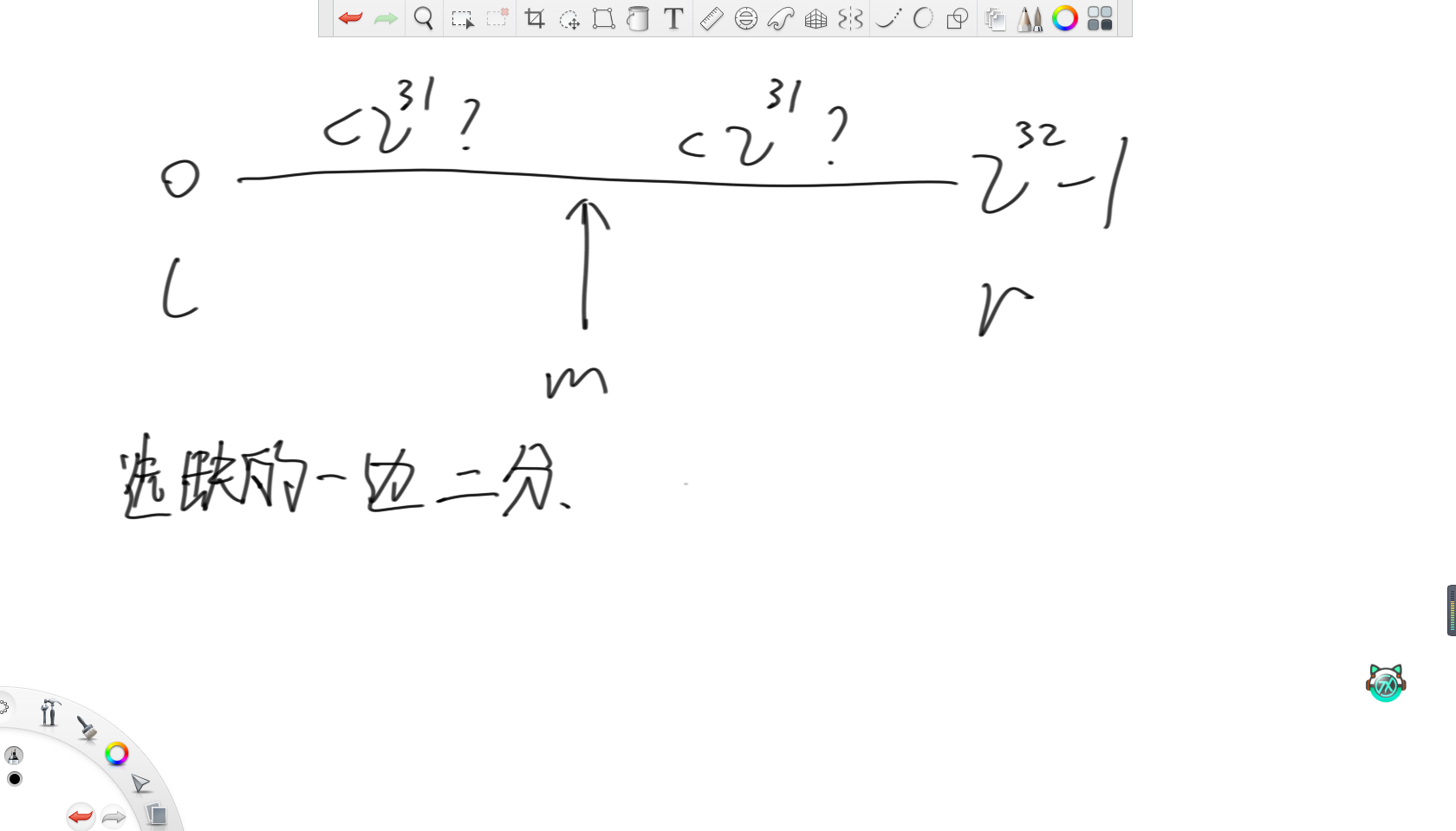
因为只需要找到一个没出现过的数，那么直接将整型的范围分别两半，用两个变量分别记录每一边的词频，然后每次选词频不满的去二分即可。

（5）内存只有3KB，如何找到这40亿个数字的中位数

如果是偶数长度，这里中位数认为是两个数中较小的那个。

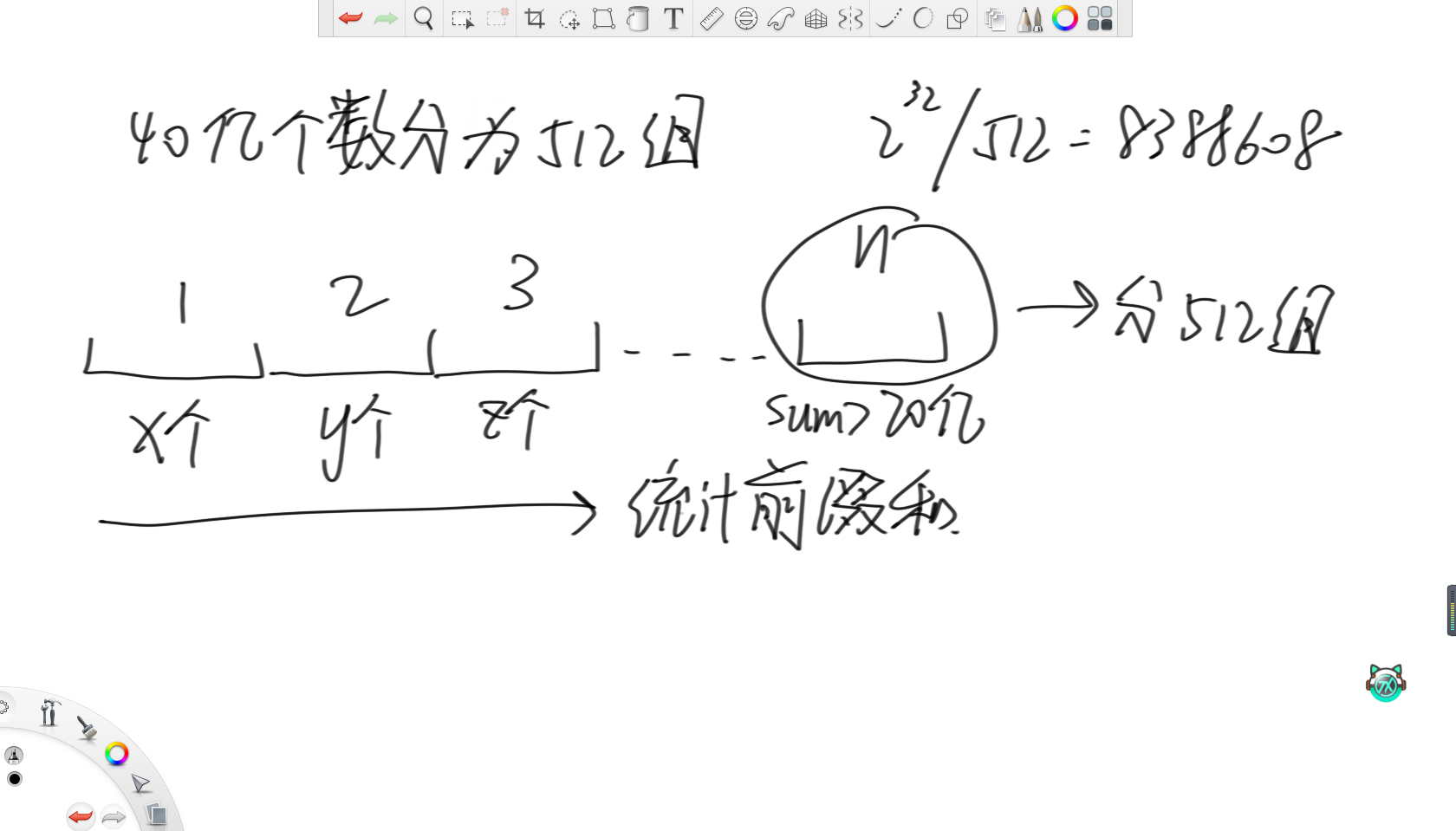
和问题（3）类似，还是将这40亿个数分为512组，每一组负责8388608个数。因为有40亿个数，那么要求的中位数就是第20亿个数，所以在统计完这512个变量的词频后，统计其前缀和。当前缀和大于20亿了，那么就说明第20亿个数来自这8388608个数范围内，那么就直接把这8388608个数分成512组，再统计词频即可。

3.文件排序问题

32位无符号整数的范围是0~4,294,967,295。有一个10G大小的文件，每一行都装着这种类型的数字，整个文件无序。给你5G的内存，请输出一个为10G大小的为原文件排序后的文件。

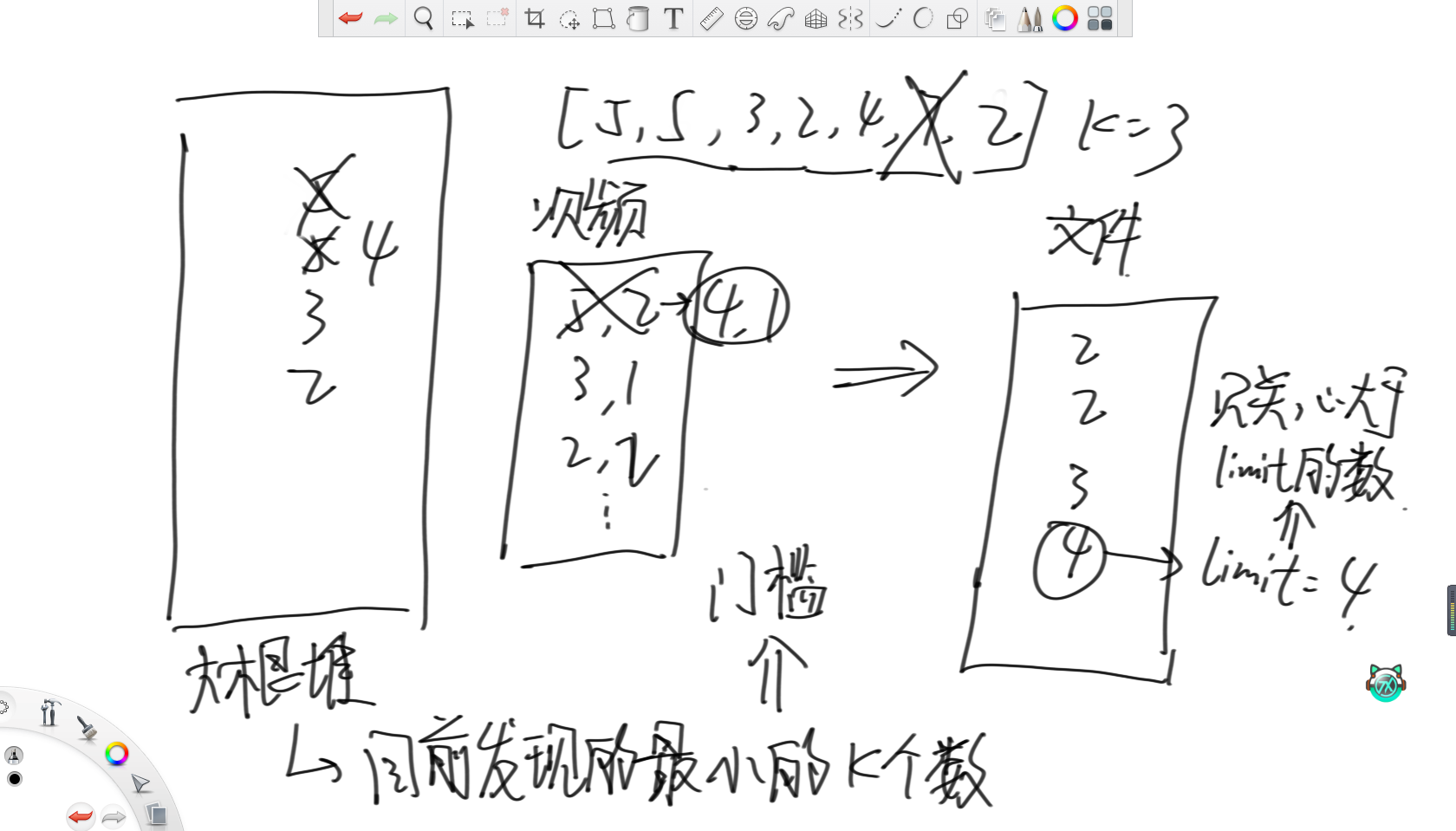
这个问题的思路是，设置一个大根堆，维护目前为止最小的k个数。其次，再设置一个map统计堆内数字的词频，这样大根堆里就不会放重复的数字。之后的操作就是遍历一遍文件，更新大根堆和这个map，然后往新文件里输出按照词频全部输出，接着用一个变量limit记录此时的最大值。那么之后再遍历文件时，就只关注大于limit的数，然后重复上述过程即可。

4.热词问题

某搜索公司一天的用户搜索词汇是100亿规模的数据量，每个搜索词汇不超过64字节。请设计一种每天从凌晨12点开始重新统计，当天任何时刻都能快速显示Top100高频词的方法。

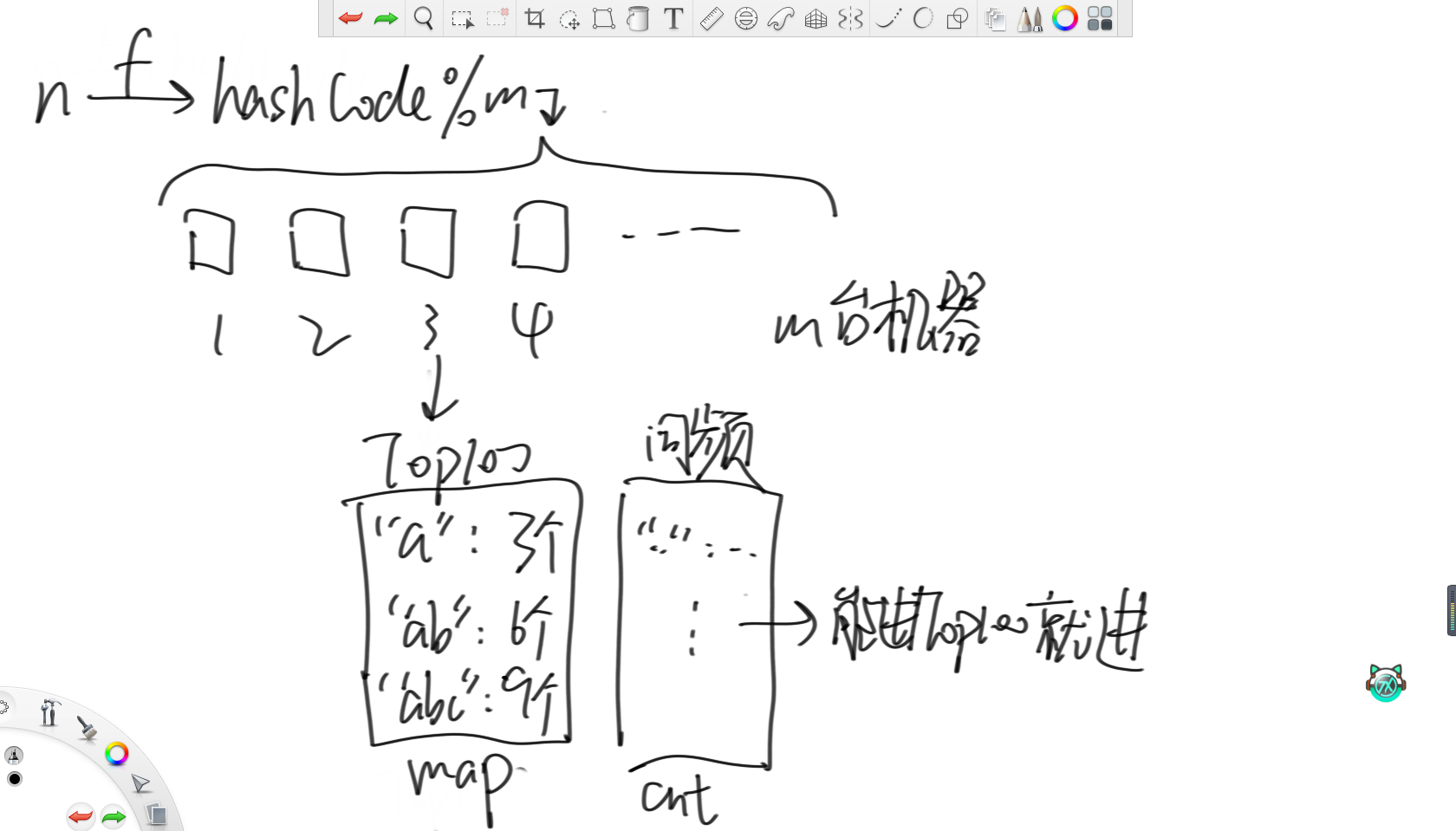
首先，对于搜索的词n，先用哈希函数转化成哈希值。之后，因为有m台机器，那么就将这个哈希值模上m分到相应的机器里。其中，每台机器里都设置一个大根堆维护词频最大的100个单词和对应的词频，每当有一个能进前100单词的词就更新。

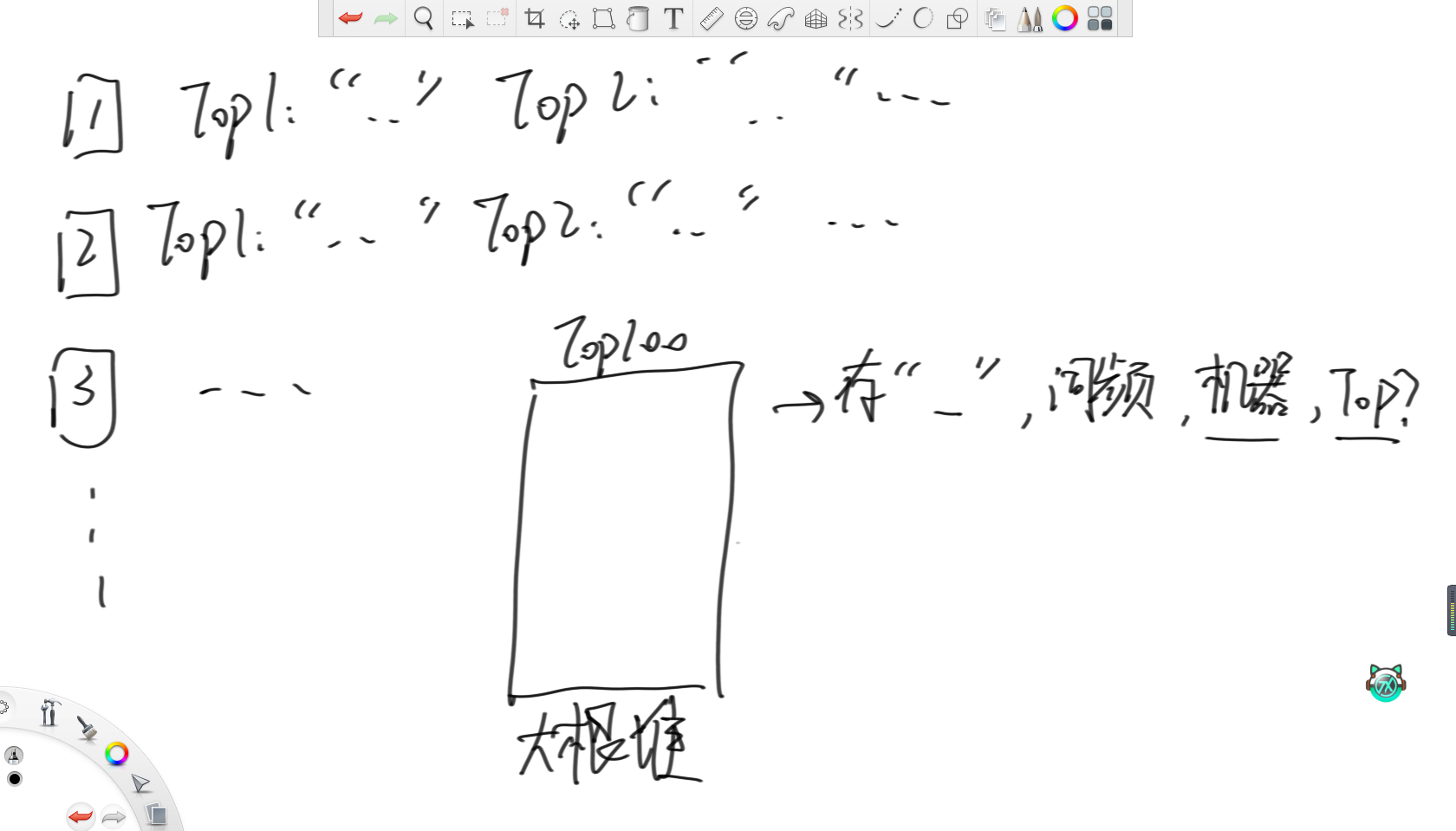
这样，每台机器都存在自己的Top100热词。之后，设置一个大根堆维护词频，同时记录单词，词频，来自的机器和在自己机器里的排名。然后，每次弹出堆顶元素作为整体Top100的单词，然后去弹出的这条记录的机器里，把下一名的单词加入大根堆，直到收集完整体的Top100单词。

5.多线程任务分配问题

给定一个存着字符串的list，每个字符串长度在1~1000之间，字符串数量20亿。每个字符串类似“hello,world,hello,cpp”，由两个hello一个world一个cpp组成。请设计一种多线程的处理方案，统计list中每个字符串切分出的单词数量，并且汇总。最终返回一个map表示每个字符串在list中的出现次数。机器资源允许最多开100个线程，使得速度尽可能快。

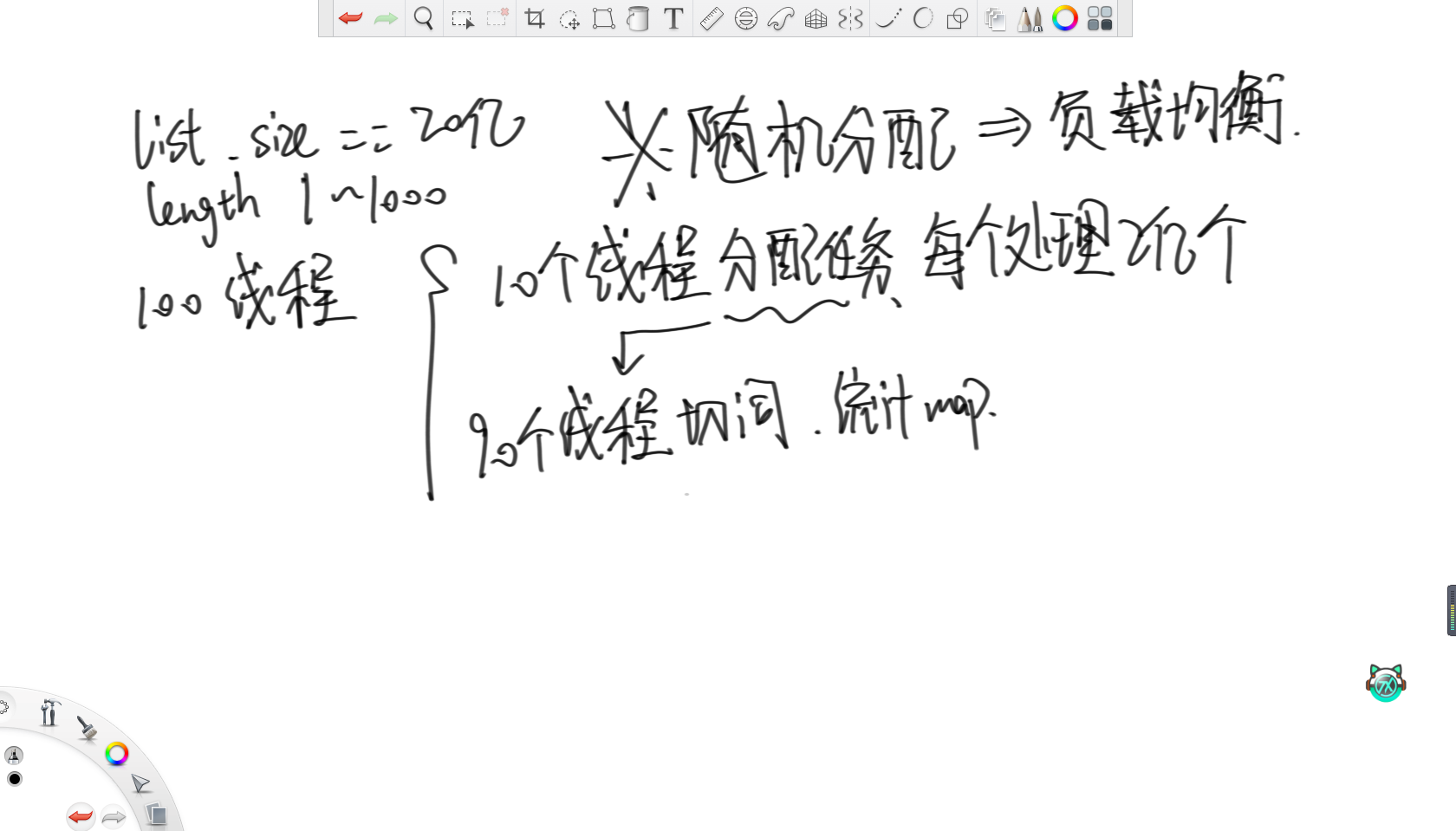
这个题的思路就比较巧妙了。

思路是就让10个线程分配任务，所以每个线程只负责读取自己范围内2亿个字符串。接着让剩余90个线程负责切词，并统计词频map。之后就是重点了，不管负载如何，纯随机给90个线程分配任务，这样不管字符串是长是短，都会随机地分配给这90个线程，所以就可以认为这90个线程的负载是均衡的。

6.设计全球的uuid系统

请设计一个只生成uuid的系统，要求理论上绝不出现相同的id，需要每秒数百万亿级别的并发，请问如何设计。

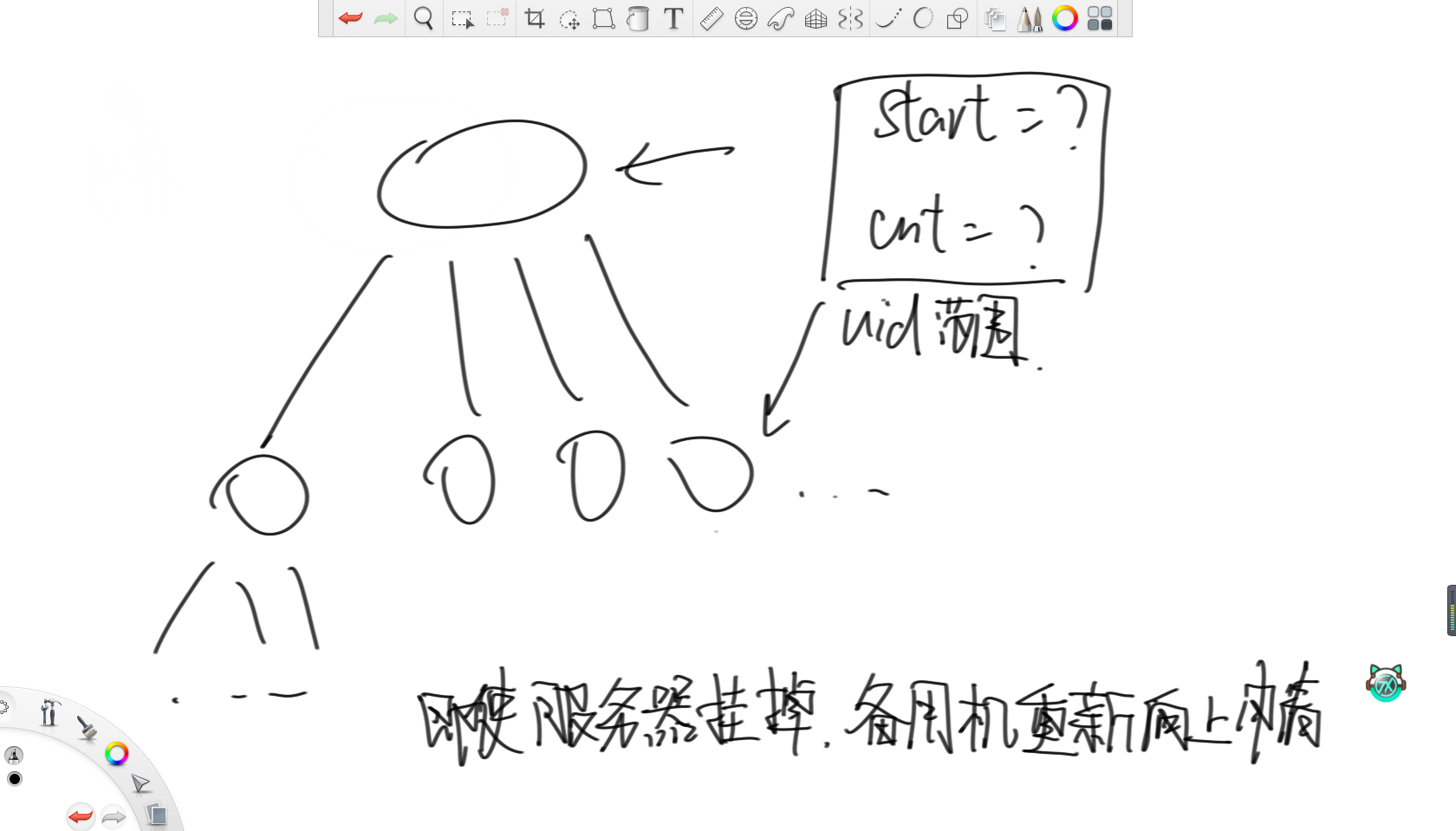
首先，顶端是世界服务器，下面有若干大洲服务器，接下来是国家服务器。对于世界服务器，设置一个start变量和cnt变量，分别记录uuid的开始值和数量，每次分配完start往后跳cnt个。之后，每次向下分配时，都传start和cnt这两个变量，通过这两个变量确认uuid的范围。同理，大洲服务器也这样向国家服务器分配，只要不够了就向上级申请。

这样设计的好处是，假如有一台服务器突然出问题了，那么当备用服务器顶上时，根本不需要进行同步，直接向上申请新的一批uuid即可。

7.囚徒生存问题

有100个犯人被关在监狱，犯人编号0~99，监狱长准备了100个盒子，盒子编号0~99。这100个盒子排成一排，放在一个房间里面，盒子编号从左往右有序排列最开始时，每个犯人的编号放在每个盒子里，两种编号一一对应，监狱长构思了一个处决犯人的计划。

监狱长打开了很多盒子，并交换了盒子里犯人的编号。交换行为完全随机，但依然保持每个盒子都有一个犯人编号。监狱长规定，每个犯人单独进入房间，可以打开50个盒子，寻找自己的编号。该犯人全程无法和其他犯人进行任何交流，并且不能交换盒子中的编号，只能打开查看。寻找过程结束后把所有盒子关上，走出房间，然后下一个犯人再进入房间，重复上述过程。监狱长规定，每个犯人在尝试50次的过程中，都需要找到自己的编号。如果有任何一个犯人没有做到这一点，100个犯人全部处决。所有犯人在一起交谈的时机只能发生在游戏开始之前，游戏一旦开始直到最后一个人结束都无法交流。请尽量制定一个让所有犯人存活概率最大的策略。