数据结构（概念及链表）

1.数据结构的概念

        程序由数据结构和算法构成，它是描述数据存储和操作的结构，是操作数据对象的方法。

        1.1.衡量代码的质量和效率

                1）时间复杂度:数据量的增长与程序运行时间的增长所呈现的比例函数关系，称为时间复杂度。以下是常见的时间复杂度：

O(1) - 常数时间复杂度：

def constant_time(n):return n * n  # 无论n多大，操作次数固定

O(n) - 线性时间复杂度：

def linear_time(n):total = 0for i in range(n):  # 循环次数与n成正比total += ireturn total

O(log n) - 对数时间复杂度：

def logarithmic_time(n):i = 1while i < n:i *= 2  # 每次循环i翻倍return i

O(n log n) - 线性对数时间复杂度

def linearithmic_time(n):result = 0for i in range(n):  # 外层循环O(n)j = 1while j < n:    # 内层循环O(log n)j *= 2result += 1return result

O(n²) - 平方时间复杂度

def quadratic_time(n):count = 0for i in range(n):      # 外层循环O(n)for j in range(n):  # 内层循环O(n)count += 1return count

O(n³) - 立方时间复杂度

def cubic_time(n):count = 0for i in range(n):          # 三层嵌套循环for j in range(n):for k in range(n):count += 1return count

O(2ⁿ) - 指数时间复杂度

def exponential_time(n):if n <= 1:return nreturn exponential_time(n-1) + exponential_time(n-2)  # 斐波那契数列的递归实现

O(n!) - 阶乘时间复杂度

def factorial_time(n):if n == 0:return 1count = 0for i in range(n):  # 每次递归调用n次count += factorial_time(n-1)return count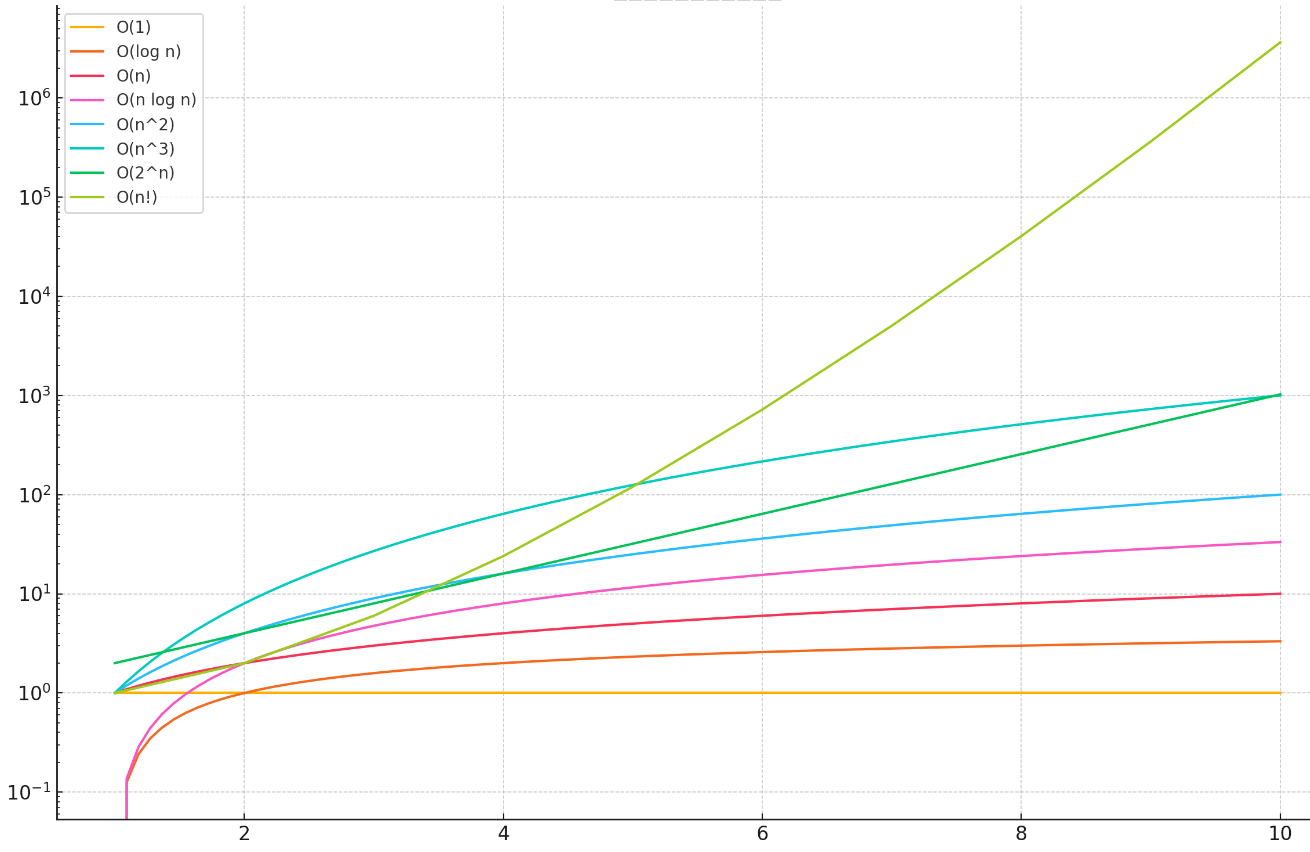

                                              （各个复杂度的运行时间与数据量的变换）

        2）空间复杂度:数据的增长与程序占据空间的增长所呈现的比例函数关系，称为空间复杂度。

1.2.数据结构

        1.2.1逻辑结构

                包括：线性结构（表，一对一），非线性结构（树，一对多），（图，多对多）

        1.2.2存储结构

                包括：顺序存储，链式存储，散列存储，索引存储

        1.2.3数据结构

                包括：顺序表，链式表，顺序栈，链式栈，顺序队列，链式队列，二叉树，邻接表，邻接矩阵

2.链表

        2.1链表的概念

                顺序表（数组）特点：存储空间连续，访问元素方便，无法利用小的空间，必须连续的大空间，顺序表元素必须为有限的（不存在无限连续的空间） 插入和删除效率低。

               链表特点：存储空间不需要连续，可以利用一些小的存储空间，但访问元素不方便，链表元素可以没有上限，插入和删除效率高。

        2.2链表的分类

                单向链表：只能通过链表节点找到后一个节点，访问链表元素的方向是单向的

                               

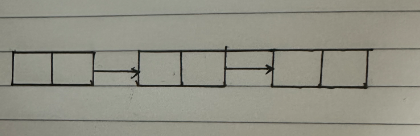
                双向链表：能够通过链表节点找到前一个节点和后一个节点

                                

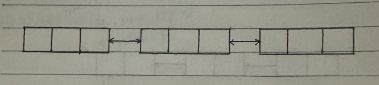
                循环链表：能够通过第一节点快速找到最后一个节点，能够通过最后一个节点快速找到第一个节点

                ​​​​​​​        ​​​​​​​        

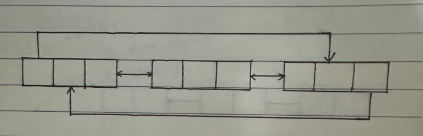
                内核链表：Linux内核所采用的一种通用的链表结构

3.单向链表

        无头链表：频繁传递二级指针，容易出错。

        有头链表：只需传递一级指针即可完成各种操作。

        3.1定义链表节点类型

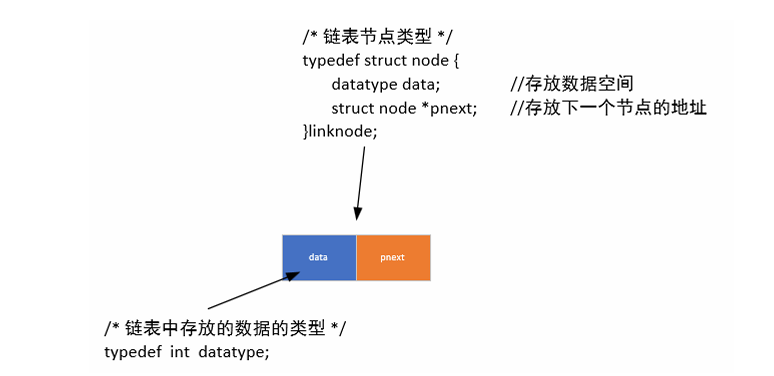
//链表存放数据的类型：
typedef int datatype;
//链表节点的类型：
typedef struct node{datatype data;struct node *pnext;
}linknode;

        3.2创立空白节点（头节点）

                创建一个空的链表节点，data不需要赋值（最好赋值)，空白节点不存放数据，主要为了保证链表操作的便利性,pnext必须赋值为NULL，表示该节点为最后一个节点,将节点地址返回。

#include"linklist.h"
#include<stdio.h>
#include<stdlib.h>
//创建一个空链表
linknode *create_empty_linklist(void)
{linknode *ptmpnode = NULL;ptmpnode = malloc(sizeof(linknode));if(NULL == ptmpnode){perror("file to malloc");return NULL;}ptmpnode->pnext = NULL;return ptmpnode;
}

        3.3链表的头插法

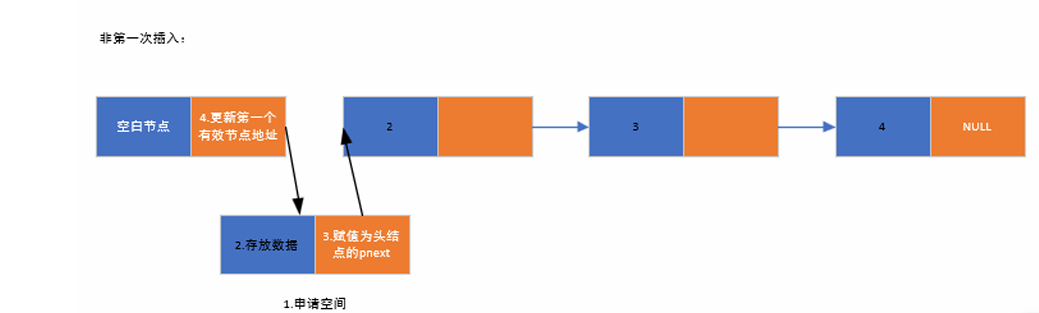
                申请新的节点空间 ，将存放的数据放入新申请的数据空间中，将新申请节点的pnext赋值为空白节点的pnext，将空白节点pnext赋值为新申请节点

//插入一个节点
int insert_head_linklist(linknode*phead,datatype tmpdata)
{linknode*ptmpnode = NULL;ptmpnode = malloc(sizeof(linknode));if (NULL == ptmpnode){perror("fail to malloc");return -1;}//存放数据ptmpnode->data = tmpdata;//存放下一个节点的地址ptmpnode->pnext = phead->pnext;//更新空白节点的下一个地址phead->pnext = ptmpnode;return 0;
}

        3.4链表的遍历

                方法一：适用于遍历所有链表节点

void show_linklist(linknode *phead){linknode *ptmpnode = NULL;ptmpnode = phead->pnext;while (ptmpnode != NULL)//判断下一个节点是不是空{printf("%d ", ptmpnode->data);ptmpnode = ptmpnode->pnext;}printf("\n");return;}

                方法二：适用于寻找最后一个链表节点

linknode* find_last_node(linknode *phead) 
{if (phead == NULL)  // 如果链表为空，直接返回NULLreturn NULL;linknode *ptmpnode = phead;  // 从头节点开始（如果phead是哨兵节点，则用 phead->pnext）while (ptmpnode->pnext != NULL)  // 如果下一个节点不是NULL，就继续向后移动{ptmpnode = ptmpnode->pnext;}return ptmpnode;  // 此时 ptmpnode 就是最后一个节点
}

        3.5从链表中删除所有某元素

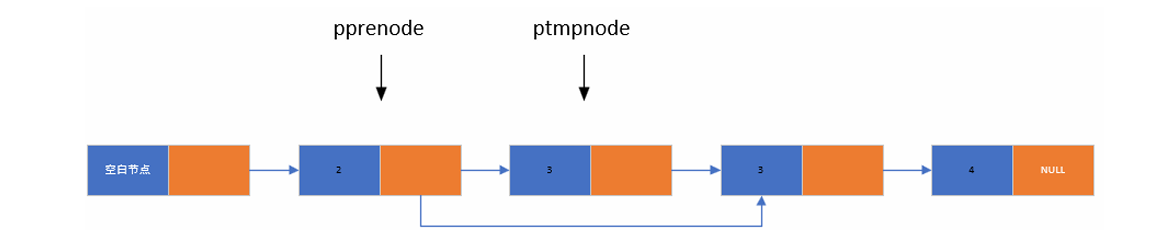
                定义两个指针ptmpnode用来遍历链表查找要删除的节点元素，pprenode永远只想 ptmpnode的前一个节点，当ptmpnode找到要删除的节点元素，让pprenode->pnext赋值为ptmpnode->pnext 并且把将要删除的节点元素释放，让ptmpnode判断下一个节点元素是否要删除，直到该指针指向NULL为止

//删除链表中所有的某一指定元素
int delete_linklist(linknode *phead, datatype tmpdata)
{linknode *pprenode = NULL;linknode *ptmpnode = NULL;pprenode = phead;ptmpnode = phead->pnext;while (ptmpnode != NULL){if (ptmpnode->data == tmpdata){pprenode->pnext = ptmpnode->pnext;free(ptmpnode);ptmpnode = pprenode->pnext;}else {ptmpnode = ptmpnode->pnext;pprenode = pprenode->pnext;}}return 0;
}

        3.6返回链表中第一个指定元素节点的地址

//数返回链表中第一个指定元素节点的地址void find_linklist(linknode *phead, datatype tmpdata){linknode *ptmpnode = NULL;linknode *pprenode = NULL;pprenode = phead;ptmpnode = pprenode->pnext;while (ptmpnode != NULL){if (ptmpnode->data == tmpdata){printf("%p\n",&pprenode->pnext);break;}else{ptmpnode = ptmpnode->pnext;pprenode = pprenode->pnext;}}return;}

        

        3.7将链表中指定元素的值更新为新值

//将链表中指定元素的值更新为新值void update_linklist(linknode *phead, datatype olddata, datatype newdata){linknode *ptmpnode = NULL;ptmpnode = phead;while (ptmpnode != NULL){if (ptmpnode->data == olddata){ptmpnode->data = newdata;}ptmpnode = ptmpnode->pnext;}return;}

        

        3.8链表的尾插法

 //尾插（顺序）void insert_tail_linklist(linknode *phead, datatype tmpdata){linknode *ptmpnode = NULL;linknode *tail = phead;//从第一个节点寻找，不能从第一个节点的下一个节点找，因为可能为空。ptmpnode = malloc(sizeof(linknode));ptmpnode->data = tmpdata;ptmpnode->pnext = NULL;while(tail ->pnext != NULL){tail = tail->pnext;}tail->pnext = ptmpnode;//将尾节点的pnext指向新建立的节点ptmpnodereturn;}

        3.9链表的销毁

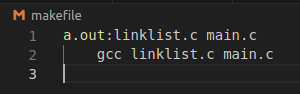
4.Makefile

        3.1 Makefile

                工程管理工具，主要用来管理代码的编译，Makefile可以根据文件中的规则来选择符合条件的代码完成编译，其能够根据依赖关系和文件修改的时间戳来决定哪些代码需要编译，哪些代码不需要重新编译。

        3.2 Makefile使用规则

                1）在工程目录下，新建一个Makefile或者makefile的文件

                 2） 在Makefile中编写对应的文件编译规则

                3） 在工程目录下使用make来调用Makefile中的规则完成代码编译

        3. 3Makefile语法规则

要生成的文件:依赖的所有文件生成命令方式

        ​​​​​​​        ​​​​​​​        ​​​​​​​