（FD Conv）Frequency Dynamic Convolution for Dense Image Prediction论文精读（逐段解析）

（FD Conv）Frequency Dynamic Convolution for Dense Image Prediction论文精读（逐段解析）

面向密集图像预测的频率动态卷积

论文地址：
https://arxiv.org/abs/2503.18783

1 北京理工大学 2 理化学研究所 3 东京大学 4 中国科学院 5 杭州电子科技大学 6 清华大学

CVPR 2025

【论文总结】：FD Conv通过三个关键模块解决了传统动态卷积中频率响应同质化和参数开销过大的问题：

1. 傅里叶不相交权重（FDW）：将参数学习从空间域转移到傅里叶域，通过将固定参数预算按频率分组并分配不相交的傅里叶索引，实现了在不增加参数成本的情况下生成具有不同频率响应的多个权重（n>10），而传统方法通常只能生成少量权重（n<10）。

2. 核空间调制（KSM）：采用双分支架构（局部通道分支+全局通道分支）生成密集调制矩阵，实现元素级的精细权重调整，相比传统方法只能进行权重级别的粗粒度调制。

3. 频率带调制（FBM）：将卷积核在频域分解为多个频率带，并为每个频率带在不同空间位置生成独立的调制系数，实现了空间变化的频率自适应处理，打破了传统卷积的空间不变性限制。

技术优势： 相比传统动态卷积方法（如CondConv、DY-Conv等）需要大幅增加参数预算（+90M、+76.5M等），FD Conv仅增加+3.6M参数就能实现更优性能，在目标检测、分割等任务上显著超越现有方法，同时具备良好的跨架构兼容性。

Abstract

While Dynamic Convolution (DY-Conv) has shown promising performance by enabling adaptive weight selection through multiple parallel weights combined with an at- tention mechanism, the frequency response of these weights tends to exhibit high similarity, resulting in high parameter costs but limited adaptability. In this work, we introduce Frequency Dynamic Convolution (FDConv), a novel approach that mitigates these limitations by learning a fixed parameter budget in the Fourier domain. FDConv di- vides this budget into frequency-based groups with disjoint Fourier indices, enabling the construction of frequencydiverse weights without increasing the parameter cost. To further enhance adaptability, we propose Kernel Spatial Modulation (KSM) and Frequency Band Modulation (FBM). KSM dynamically adjusts the frequency response of each filter at the spatial level, while FBM decomposes weights into distinct frequency bands in the frequency domain and modulates them dynamically based on local content. Extensive experiments on object detection, segmentation, and classification validate the effectiveness of FDConv. We demonstrate that when applied to ResNet-50, FDConv achieves superior performance with a modest increase of $+3.6M$ parameters, outperforming previous methods that require substantial increases in parameter bud- gets (e.g., CondConv $+9OM,$ , $KW+76.5M,$ ). Moreover, FDConv seamlessly integrates into a variety of architectures, including ConvNeXt, Swin-Transformer, offering a flexible and efficient solution for modern vision tasks. The code is made publicly available at https://github.com/LinweiChen/FDConv .

【翻译】虽然动态卷积（DY-Conv）通过多个并行权重结合注意力机制实现自适应权重选择，展现了良好的性能，但这些权重的频率响应往往表现出高度相似性，导致参数成本高但适应性有限。在这项工作中，我们引入了频率动态卷积（FDConv），这是一种通过在傅里叶域中学习固定参数预算来缓解这些限制的新方法。FDConv将这个预算划分为基于频率的组，每组具有不相交的傅里叶索引，从而能够在不增加参数成本的情况下构建频率多样化的权重。为了进一步增强适应性，我们提出了核空间调制（KSM）和频带调制（FBM）。KSM在空间层面动态调整每个滤波器的频率响应，而FBM将权重在频域中分解为不同的频带，并基于局部内容对其进行动态调制。在目标检测、分割和分类任务上的大量实验验证了FDConv的有效性。我们证明，当应用于ResNet-50时，FDConv仅增加$+3.6M$参数就实现了优越的性能，超越了需要大幅增加参数预算的先前方法（例如，CondConv $+90M$，KW $+76.5M$）。此外，FDConv可以无缝集成到各种架构中，包括ConvNeXt、Swin-Transformer，为现代视觉任务提供了灵活高效的解决方案。代码已在 https://github.com/LinweiChen/FDConv 公开发布。

【解析】动态卷积虽然使用多个并行权重和注意力机制来实现自适应选择，但存在频率响应同质化的缺陷。这种同质化现象说明多个权重虽然在数量上增加了，但在频率特性上却缺乏足够的差异性，FDConv的核心创新在于将参数学习从传统的空间域转移到傅里叶域。通过在傅里叶域中建立固定的参数预算，并将其划分为具有不相交傅里叶索引的频率组，这种设计确保了每个权重组在频率特性上的独特性。这种方法的数学基础是傅里叶变换的正交性，不相交的频率索引保证了不同权重在频率响应上的互补性而非重复性。KSM和FBM作为两个重要的增强模块，分别在空间域和频域提供了精细化的调制能力。KSM通过在卷积核的空间层面进行元素级调制，实现了对每个滤波器频率响应的精确控制。这种空间层面的调制允许模型根据输入特征的空间分布来调整频率响应特性。FBM则在频域中实现权重的频带分解和动态调制，这种设计使得模型能够根据局部内容特征来选择性地强化或抑制特定频带，从而实现空间变化的频率处理能力。

1. Introduction

Convolution, the core operation in ConvNets, has driven decades of advancement in computer vision [ 1 , 3 – 6 , 14 , 18 , 23 , 29 , 35 , 38 , 44 , 47 , 61 , 77 , 80 ]. Essential for capturing local patterns and building hierarchical representations, it remains fundamental in modern architectures [ 11 , 47 , 62 , 71 ].

【翻译】卷积作为卷积神经网络的核心操作，推动了计算机视觉数十年的发展[ 1 , 3 – 6 , 14 , 18 , 23 , 29 , 35 , 38 , 44 , 47 , 61 , 77 , 80 ]。它对于捕获局部模式和构建层次化表示至关重要，在现代架构中仍然是基础性的[ 11 , 47 , 62 , 71 ]。

【解析】卷积运算通过局部感受野，能有效提取图像中的空间局部特征，这种局部性处理机制与人类视觉系统的感知方式高度一致。层次化表示的构建是通过多层卷积的级联实现的，每一层都能在前一层特征的基础上提取更加抽象和复杂的特征。从数学角度来看，卷积运算具有平移不变性，无论目标物体在图像中的位置如何变化，卷积核都能够检测到相同的特征模式。

Building upon the success of standard convolution, Dynamic Convolution (DY-Conv) [ 63 , 73 ] offers a more adaptive and efficient approach. Unlike standard convolution with fixed weights, DY-Conv uses multiple parallel weights combined by an attention module, allowing sample-specific weight adaptation with minimal extra computation.

【翻译】基于标准卷积的成功，动态卷积（DY-Conv）[ 63 , 73 ]提供了一种更加自适应和高效的方法。与使用固定权重的标准卷积不同，DY-Conv使用多个并行权重通过注意力模块进行组合，允许针对样本的权重自适应，同时只需最小的额外计算。

【解析】动态卷积打破了传统卷积权重固定的限制。在标准卷积中，每个卷积核的权重在训练完成后就固定不变，这说明模型对所有输入都使用相同的特征提取模式。动态卷积通过引入多个并行的卷积权重矩阵，并设计注意力机制来动态选择和组合这些权重，实现了输入依赖的特征提取。具体而言，注意力模块会根据当前输入特征计算出权重系数，这些系数用于对多个并行权重进行加权融合，从而产生针对当前输入最适合的卷积核。其数学优势在于增加了模型的表达能力，使得同一个卷积层能够根据输入内容的不同而展现出不同的特征提取行为，而计算开销的增加主要来自于注意力模块的轻量级计算，相比于特征提取能力的提升，这种计算开销是可以接受的。

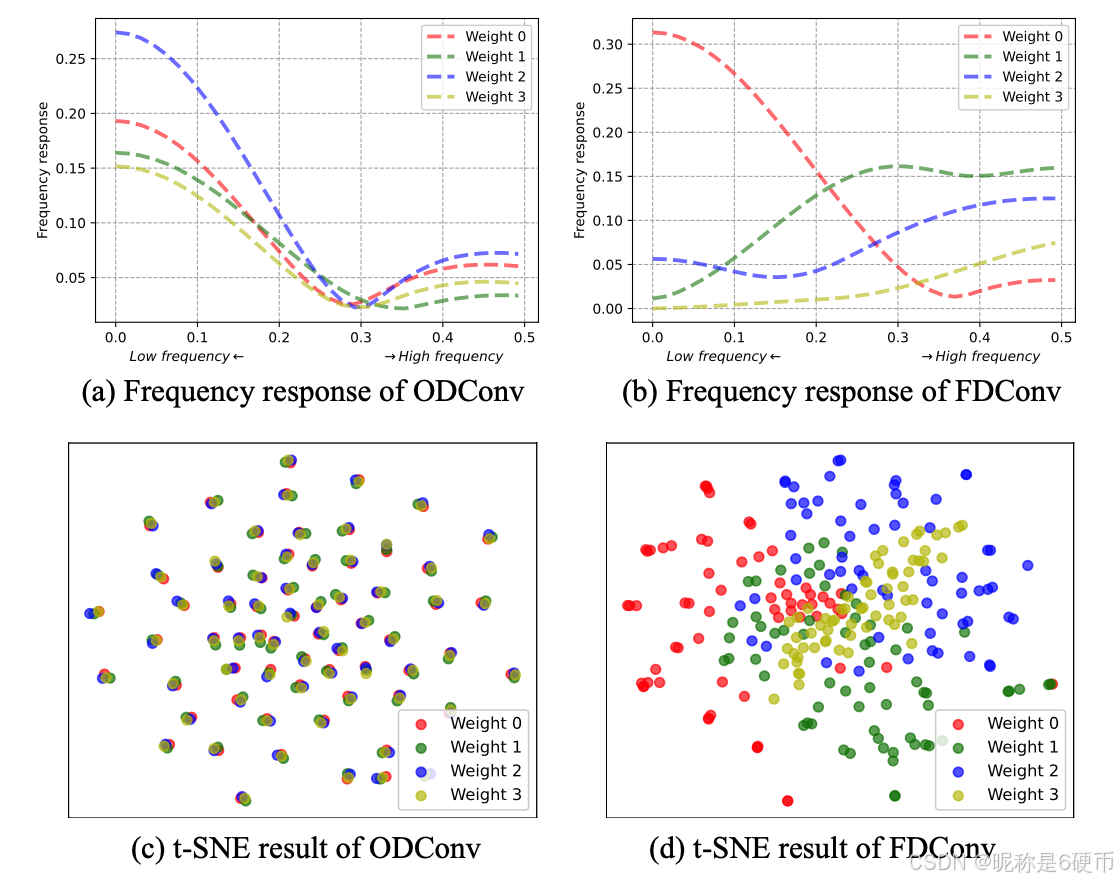
However, our analysis in Figure 1 reveals that traditional dynamic convolution [ 31 , 32 , 63 , 73 ] lack of fre- quency responses diversity in their parallel weights. As shown in Figure 1(a) , these weights exhibit highly similar frequency responses, while the t-SNE visualization in Figure 1© indicates that filters within ODConv [ 32 ] are clustered closely. Despite a significant increase in parameters ( e.g ., $4\times$ in [ 31 , 32 , 63 , 73 ]), this limited frequency diversity reduces the model’s ability to adaptively capture frequency information. For example, extracting low-frequency components helps suppress noise [ 3 ], while high-frequency components capture details and boundaries [ 2 , 36 , 51 , 78 ], which are vital for foreground-background differentiation.

【翻译】然而，我们在图1中的分析表明，传统的动态卷积[ 31 , 32 , 63 , 73 ]在其并行权重中缺乏频率响应的多样性。如图1(a)所示，这些权重表现出高度相似的频率响应，而图1©中的t-SNE可视化显示ODConv[ 32 ]中的滤波器聚集得很紧密。尽管参数显著增加（例如，在[ 31 , 32 , 63 , 73 ]中增加了$4\times$），这种有限的频率多样性降低了模型自适应捕获频率信息的能力。例如，提取低频分量有助于抑制噪声[ 3 ]，而高频分量捕获细节和边界[ 2 , 36 , 51 , 78 ]，这对前景-背景区分至关重要。

【解析】频率响应分析揭示了传统动态卷积的缺陷。当多个并行权重在频域中表现出高度相似的特性时，说明虽然权重在空间域可能看起来不同，但它们在频率域的行为却趋于一致。这种现象的数学本质可以通过傅里叶变换来理解：每个卷积核都可以通过傅里叶变换转换到频域，其频率响应曲线描述了该核对不同频率成分的敏感程度。当多个权重的频率响应曲线高度重叠时，说明它们在处理不同频率信息时的表现几乎相同，这就造成了参数冗余。t-SNE可视化进一步证实了这一点，紧密聚集的滤波器分布说明学习到的特征表示缺乏多样性。频率信息的重要性在于不同频率成分承载着不同类型的视觉信息：低频成分主要包含图像的整体结构和光照变化，对噪声具有天然的抑制作用；高频成分则包含边缘、纹理等细节信息，这些信息对于目标检测和分割任务中的精确边界定位至关重要。因此，缺乏频率多样性的动态卷积无法有效利用这些不同频率成分的互补信息，限制了模型的表达能力。

To address these limitations, we propose Frequency Dynamic Convolution (FDConv), as shown in Figure 2 . It is designed to enhance frequency adaptability without incurring excessive parameter overhead. Our approach is based on three core modules: Fourier Disjoint Weight, Kernel Spatial Modulation, and Frequency Band Modulation.

【翻译】为了解决这些限制，我们提出了频率动态卷积（FDConv），如图2所示。它旨在增强频率适应性而不会产生过多的参数开销。我们的方法基于三个核心模块：傅里叶不相交权重、核空间调制和频带调制。

【解析】FDConv的设计理念是在保持参数效率的前提下实现频率域的自适应性。三个核心模块各自功能：傅里叶不相交权重模块负责在频域中构建具有不同频率特性的权重；核空间调制模块在空间层面提供精细化的权重调整；频带调制模块则在频域中实现空间变化的频率处理。

Unlike traditional methods [ 32 , 63 , 73 ], which learn weights in the spatial domain, the Fourier Disjoint Weight (FDW) constructs kernel weights by learning spectral coefficients in the Fourier domain. These coefficients are divided into frequency-based groups, each with a disjoint set of Fourier indices. An inverse Discrete Fourier Transform (iDFT) is then applied to these groups, converting them into spatial weights. This disjoint grouping enables each weight to exhibit distinct frequency responses (as shown in Figure 1(b) ), ensuring high diversity among the learned weights (also shown in Figure 1(d) ).

【翻译】与在空间域中学习权重的传统方法[ 32 , 63 , 73 ]不同，傅里叶不相交权重（FDW）通过在傅里叶域中学习谱系数来构建核权重。这些系数被划分为基于频率的组，每组具有不相交的傅里叶索引集合。然后对这些组应用离散傅里叶逆变换（iDFT），将它们转换为空间权重。这种不相交分组使得每个权重能够表现出不同的频率响应（如图1(b)所示），确保了学习权重之间的高度多样性（如图1(d)所示）。

【解析】传统动态卷积直接在空间域中学习多个并行权重矩阵，这种方法虽然直观但容易导致权重在频率特性上的同质化。FDW通过在傅里叶域中学习谱系数，利用了傅里叶变换的数学特性来确保权重的频率多样性。具体而言，每个权重组被分配一组不相交的傅里叶索引，这种分配策略基于傅里叶基函数的正交性原理。由于不同的傅里叶索引对应于不同的频率成分，因此分配给不同组的索引集合在数学上保证了它们在频率域中的不重叠性。通过iDFT将这些频域系数转换回空间域时，每个权重组自然地继承了其对应频率成分的特性，从而在空间域中表现出不同的频率响应模式。这种方法的数学优势在于它能够在固定的参数预算下生成具有明确频率差异化的权重，避免了传统方法中权重学习过程的随机性可能导致的频率响应收敛问题。

Figure 1. Weight frequency responses and t-SNE analyses. We set the number of weights to 4 to align with ODConv [ 32 ]. (a) The frequency responses of the four parallel weights in ODConv are highly similar, indicating limited diversity. (b) In contrast, FDConv shows distinct frequency responses for each weight, spanning different parts of the frequency spectrum. © The t-SNE plot for ODConv reveals that the filters in the four weights are closely clustered, suggesting a lack of diversity. (d) The t-SNE plot for FDConv shows that the filters in the four weights have different distributions, indicating greater diversity.

【翻译】图1. 权重频率响应和t-SNE分析。我们将权重数量设置为4以与ODConv[ 32 ]保持一致。(a) ODConv中四个并行权重的频率响应高度相似，表明多样性有限。(b) 相比之下，FDConv显示每个权重具有不同的频率响应，跨越频谱的不同部分。© ODConv的t-SNE图显示四个权重中的滤波器紧密聚集，表明缺乏多样性。(d) FDConv的t-SNE图显示四个权重中的滤波器具有不同的分布，表明更大的多样性。

【解析】图1提供了FDConv相对于传统动态卷积方法在频率多样性方面优势的直观表示。频率响应分析通过将每个卷积核的权重进行傅里叶变换来计算其对不同频率成分的敏感度，这种分析方法能够揭示权重在频域中的行为特征。ODConv的频率响应曲线几乎重叠，说明尽管有四个不同的权重，但它们在频率处理上的能力高度相似，这种相似性削弱了多权重设计的初衷。FDConv的频率响应曲线则呈现出明显的差异化，每个权重在不同的频率区间内显示出峰值响应，这种差异化确保了每个权重能够专门处理特定的频率信息。t-SNE可视化从另一个角度验证了这一点，通过将高维的滤波器特征映射到二维空间，可以观察到ODConv的滤波器在特征空间中形成紧密的聚类，而FDConv的滤波器则分布在更广阔的特征空间中，这种分散的分布模式直接反映了权重学习到的特征表示的多样性和丰富性。

Kernel Spatial Modulation (KSM) enhances flexibility by precisely adjusting the frequency response of each filter at the spatial level within the kernel. By combining local and global channel information, KSM generates a dense matrix of modulation values that finely tunes each individual weight element. This fine-grained control enables FDConv to dynamically adapt each filter element, allowing for frequency response adjustment across the entire kernel.

【翻译】核空间调制（KSM）通过在核内的空间层面精确调整每个滤波器的频率响应来增强灵活性。通过结合局部和全局通道信息，KSM生成一个密集的调制值矩阵，精细调整每个单独的权重元素。这种细粒度控制使FDConv能够动态适应每个滤波器元素，允许在整个核中进行频率响应调整。

【解析】KSM的设计思想是在卷积核的最小粒度级别实现频率调制。传统的动态卷积通常在权重级别进行调制，也就是对整个权重矩阵应用一个标量系数。而KSM则深入到权重矩阵的每一个元素，为每个元素生成独立的调制系数。这种元素级的调制能力源于对局部和全局通道信息的综合利用：局部信息捕获当前空间位置的特征特性，全局信息提供整体的上下文约束。通过将这两类信息融合，KSM能够生成一个与权重矩阵同样大小的调制矩阵，其中每个位置的调制值都是针对对应权重元素的频率特性进行的精确调整。这种精细化调制的数学意义在于它能够在不改变权重矩阵基本结构的前提下，通过元素级的乘法运算来实现频率响应的空间变化控制，从而使得同一个卷积核在处理不同区域的特征时能够展现出不同的频率敏感性。

Frequency Band Modulation (FBM) decomposes weights into distinct frequency bands in the frequency domain, enabling spatially variant frequency modulation. It allows each frequency band of the weight to be adjusted independently across spatial locations. Unlike traditional dynamic convolutions, which apply fixed frequency responses across spatial dimensions, FBM decomposes weights into distinct frequency bands and dynamically modulates them based on local content. This design enables the model to selectively emphasize or suppress frequency bands across different regions, adaptively capturing diverse frequency information in a spatially variant manner.

【翻译】频带调制（FBM）在频域中将权重分解为不同的频带，实现空间变化的频率调制。它允许权重的每个频带在不同空间位置独立调整。与在空间维度上应用固定频率响应的传统动态卷积不同，FBM将权重分解为不同的频带，并基于局部内容对其进行动态调制。这种设计使模型能够在不同区域选择性地强调或抑制频带，以空间变化的方式自适应地捕获多样化的频率信息。

【解析】FBM解决了传统动态卷积在空间频率处理上的局限性。传统动态卷积虽然能够实现权重的动态选择，但这种选择在空间上是一致的，说明无论输入特征图的哪个空间位置，都会应用相同的频率处理策略。FBM通过在频域中对权重进行频带分解，将一个完整的卷积核分解为多个频带分量，每个分量专门处理特定频率范围的信息。这种分解基于傅里叶变换的频率分析能力，通过频域滤波技术将权重的不同频率成分分离出来。更重要的是，FBM为每个频带分量设计了空间变化的调制机制，这种机制能够根据输入特征图中每个空间位置的局部内容特性来动态调整对应频带的权重。具体而言，对于图像中的边缘区域，模型可能会增强高频分量的权重以更好地捕获边缘信息；而对于平滑区域，模型可能会增强低频分量的权重以更好地处理纹理信息。这种空间自适应的频率调制机制使得FDConv能够在单一卷积操作中实现多种频率处理策略的空间分布，从而显著提升了模型对复杂视觉场景的适应能力。

Moreover, unlike previous works [ 32 , 63 , 73 ], which increase parameter costs by a factor of $n$ (where $n$ is the number of weights, typically $n<10$ [ 32 , 63 , 73 ]), our FDConv maintains a fixed parameter budget while generating a large number of frequency-diverse weight kernels $(n>10)$ ) by dividing parameters in the Fourier domain into disjoint frequency-based groups. This design allows the model to efficiently learn weights with distinct frequency responses without burdening parameter cost.

【翻译】此外，与之前的工作[ 32 , 63 , 73 ]不同，那些方法将参数成本增加$n$倍（其中$n$是权重的数量，通常$n<10$[ 32 , 63 , 73 ]），我们的FDConv在保持固定参数预算的同时，通过在傅里叶域中将参数划分为不相交的基于频率的组来生成大量频率多样化的权重核$(n>10)$。这种设计允许模型在不增加参数成本负担的情况下高效地学习具有不同频率响应的权重。

【解析】FDConv实现了参数效率的突破。传统动态卷积方法为了获得多个并行权重，必须为每个权重分配独立的参数空间，这导致参数量与权重数量成正比增长。当需要$n$个权重时，总参数量就会增加$n$倍，这种线性增长很快就会变得不可承受，因此传统方法通常限制权重数量在10个以内。FDConv通过傅里叶域的不相交分组策略彻底改变了这种参数分配模式。在傅里叶域中，一个完整的频谱可以被分解为多个不重叠的频率区间，每个区间对应不同的频率成分。通过将学习参数按照这些频率区间进行分组，每组参数只负责特定频率范围的权重构建。由于这些分组在频域中是不相交的，它们在数学上保证了生成权重的频率多样性。更重要的是，通过逆傅里叶变换，可以从这些相对较少的频域参数中重构出具有明确频率特性的空间域权重。这种方法的数学优势在于利用了傅里叶变换的信息压缩特性：频域中的少量参数能够有效地表示空间域中复杂的权重模式。因此，FDConv能够在相同的参数预算下生成比传统方法更多数量的权重，同时保证这些权重在频率特性上的根本性差异。

Extensive experiments on object detection, instance segmentation, semantic segmentation, and image classification validate the effectiveness of FDConv. For example, when applied to ResNet-50, FDConv achieves superior performance with a modest increase of +3.6M parameters, outperforming previous methods that require substantial increases in parameter budgets ( e.g ., CondConv +90M , DY-Conv +75.3M, ODConv +65.1M , KW +76.5M) [ 31 , 32 , 63 , 73 ]. FDConv can be seamlessly integrated into various architectures, including ConvNeXt and Swin Transformer, where it replaces the linear layer (as a $1\times 1$ convolution), offering a versatile and efficient solution.

【翻译】在目标检测、实例分割、语义分割和图像分类上的大量实验验证了FDConv的有效性。例如，当应用于ResNet-50时，FDConv仅增加+3.6M参数就实现了优越的性能，超越了需要大幅增加参数预算的之前方法（例如，CondConv +90M，DY-Conv +75.3M，ODConv +65.1M，KW +76.5M）[ 31 , 32 , 63 , 73 ]。FDConv可以无缝集成到各种架构中，包括ConvNeXt和Swin Transformer，其中它替换线性层（作为$1\times 1$卷积），提供了一个多功能且高效的解决方案。

• We conduct a comprehensive exploration of dynamic convolution using frequency analysis. Our findings reveal that the parameters of traditional dynamic convolution methods exhibit high homogeneity in frequency response across learned parallel weights, resulting in high parameter redundancy and limited adaptability.

【翻译】我们使用频率分析对动态卷积进行了全面探索。我们的发现表明，传统动态卷积方法的参数在学习的并行权重间表现出频率响应的高度同质性，导致高参数冗余和有限的适应性。

【解析】作者采用频域分析方法来审视动态卷积的内在机制，传统的动态卷积评估主要关注空间域的性能表现，而频域分析能够揭示权重参数在频率特性上的根本问题。通过傅里叶变换将空间域的卷积核转换到频域进行分析，研究者发现了一个关键问题：尽管动态卷积设计了多个并行的权重分支，但这些权重在频域中表现出惊人的相似性。具体来说，不同权重分支的频率响应曲线几乎重叠，说明它们对各个频率成分的敏感度基本一致。这种频率响应的同质性从数学角度解释了为什么动态卷积虽然增加了大量参数，但性能提升却有限的根本原因。频率响应的高度相似性说明多个权重实际上在做重复的工作，它们都倾向于处理相同的频率信息，而不是分工合作处理不同的频率成分。这种现象导致了严重的参数冗余，因为增加的参数并没有带来功能上的多样性，同时也限制了模型的适应性，因为模型无法灵活地针对不同类型的频率信息进行专门化处理。

• We introduce the Fourier Disjoint Weight (FDW), Kernel Spatial Modulation (KSM), and Frequency Band Modulation (FBM) strategies. FDW constructs multiple weights with diversified frequency responses without increasing the parameter cost, KSM enhances the representation power by adjusting weights element-wise, and FBM improves convolution by precisely extracting frequency bands in a spatially variant manner.

【翻译】我们引入了傅里叶不相交权重（FDW）、核空间调制（KSM）和频带调制（FBM）策略。FDW在不增加参数成本的情况下构建具有多样化频率响应的多个权重，KSM通过逐元素调整权重来增强表示能力，FBM通过以空间变化的方式精确提取频带来改进卷积。

【解析】FDW通过在傅里叶域中进行不相交的参数分组来确保生成的权重具有本质上不同的频率特性，利用了傅里叶基函数的正交性：通过将参数按照不同的傅里叶索引进行分组，每组参数天然地对应于不同的频率成分，从而在逆变换回空间域时自动保证了权重的频率多样性。KSM在FDW的基础上提供了更精细的控制机制，它不再满足于权重级别的调制，而是深入到权重矩阵的每个元素级别。通过生成与权重矩阵同维度的调制矩阵，KSM能够为每个权重元素提供个性化的调制系数，这种元素级的精确控制使得模型能够在保持权重基本频率特性的同时，根据具体的输入内容进行微调。FBM则从另一个维度扩展了频率控制能力，它将权重在频域中分解为多个频带，并为每个频带设计空间自适应的调制机制。这种设计使得模型能够根据输入特征图中不同空间位置的内容特性，动态调整对各个频带的处理强度，实现了真正的空间-频率联合自适应处理。

• We demonstrate that our approach can be easily integrated into existing ConvNets and vision transformers. Comprehensive experiments on segmentation tasks show that it surpasses previous state-of-the-art dynamic convolution methods, requiring only a minor increase in parameters, consistently demonstrating its effectiveness.

【翻译】我们证明了我们的方法可以轻松集成到现有的ConvNets和视觉变换器中。在分割任务上的综合实验表明，它超越了以前最先进的动态卷积方法，仅需要轻微的参数增加，一致地证明了其有效性。

2. Related Work

Feature Recalibration. Feature recalibration through attention mechanisms has proven highly effective in deep learning models. Methods such as RAN [ 64 ], SE [ 26 ], CBAM [ 69 ], GE [ 25 ], SRM [ 30 ], ECA [ 67 ], and SimAtt [ 74 ] focus on adaptively emphasizing informative features or suppressing irrelevant ones across channels and spatial dimensions of the feature map, i.e ., channel and spatial attention. In contrast, our approach introduces frequency-specific recalibration for convolution weights.

【翻译】特征重标定。通过注意力机制进行特征重标定在深度学习模型中已被证明是高度有效的。诸如RAN [ 64 ]、SE [ 26 ]、CBAM [ 69 ]、GE [ 25 ]、SRM [ 30 ]、ECA [ 67 ]和SimAtt [ 74 ]等方法专注于在特征图的通道和空间维度上自适应地强调信息性特征或抑制无关特征，即通道和空间注意力。相比之下，我们的方法为卷积权重引入了频率特定的重标定。

【解析】特征重标定是深度学习中的一个重要概念，其核心思想是通过动态调整特征的重要性来提升模型的表达能力。传统的特征重标定方法主要在空间域进行操作，通过分析特征图在通道维度和空间位置维度上的重要性分布来生成注意力权重。这些方法的数学基础通常基于全局平均池化或全局最大池化来聚合空间信息，然后通过多层感知机或卷积操作来学习重标定权重。然而，这些传统方法存在一个根本性的局限：它们仅考虑了特征在空间域中的分布特性，而忽略了特征在频域中的重要信息。不同频率成分对于不同的视觉任务具有不同的重要性，例如低频信息主要包含形状和轮廓信息，而高频信息则包含纹理和边缘细节。FDConv的创新之处在于将重标定机制扩展到频域，通过分析和调整卷积权重在不同频率成分上的响应强度，实现了更精细和更有针对性的特征重标定策略。

Dynamic Weight Networks. Recently, dynamic networks have shown to be effective in various computer vision tasks. Dynamic Filter Networks [ 28 ] and Kernel Prediction Net- works [ 53 ] generate sample-adaptive filters conditioned on the input. In contrast, Hypernetworks [ 20 ] generate weights for a larger recurrent network instead of ConvNets. Building upon similar idea, CARAFE [ 66 ] and Involution [ 33 ] have developed efficient modules that predict spatially variant convolution weights.

【翻译】动态权重网络。最近，动态网络在各种计算机视觉任务中已被证明是有效的。动态滤波器网络[ 28 ]和核预测网络[ 53 ]根据输入生成样本自适应的滤波器。相比之下，超网络[ 20 ]为更大的循环网络而不是ConvNets生成权重。基于类似的思想，CARAFE [ 66 ]和Involution [ 33 ]已经开发出能够预测空间变化卷积权重的高效模块。

【解析】动态权重网络代表了深度学习架构设计的一个重要发展方向，其根本目标是打破传统神经网络中权重参数固定不变的限制。传统的卷积神经网络在训练完成后，其权重参数就被固定下来，无论输入内容如何变化，网络都使用相同的权重进行处理。动态权重网络通过引入权重生成机制，使网络能够根据当前输入的特性动态调整其权重参数。这种自适应性体现在多个层面：样本自适应性允许网络为不同的输入样本生成不同的权重，空间自适应性使网络能够为特征图的不同空间位置使用不同的权重。动态滤波器网络和核预测网络通过额外的子网络来预测主网络的权重，这种预测通常基于输入特征的全局或局部统计信息。超网络则采用了更加通用的框架，通过一个较小的网络来生成另一个较大网络的所有权重，这种方法在循环神经网络中特别有效。CARAFE和Involution进一步扩展了这一思想，通过预测空间变化的权重来实现更精细的特征处理，但这些方法都存在参数开销大和计算复杂度高的问题。

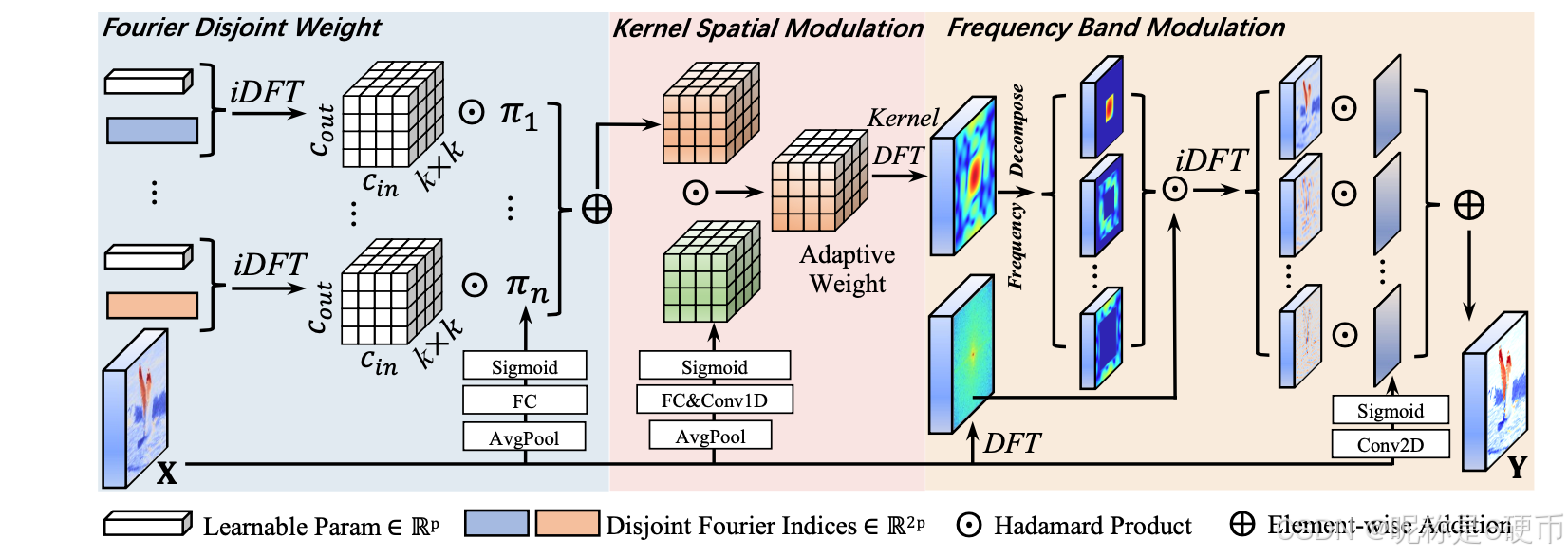
Figure 2. Illustration of the proposed Frequency Dynamic Convolution, which consists of the Fourier Disjoint Weight (FDW), Kernel Spatial Modulation (KSM), and Frequency Band Modulation (FBM) modules. FC indicates fully connected layer.

【翻译】图2. 所提出的频率动态卷积示意图，包括傅里叶不相交权重（FDW）、核空间调制（KSM）和频带调制（FBM）模块。FC表示全连接层。

【解析】图2展示了FDConv的整体架构设计，通过三个核心模块的协同工作来实现频率域的动态卷积。从系统架构的角度来看，这三个模块形成了一个完整的处理流水线：FDW模块负责在保持参数效率的前提下生成具有不同频率特性的多个权重，这是整个系统的基础；KSM模块在FDW生成的权重基础上进行元素级的精细调制，提供空间维度上的自适应性；FBM模块则从频域角度对权重进行分解和调制，实现频率维度上的自适应性。这种三层次的处理策略确保了FDConv能够同时在参数效率、空间适应性和频率适应性三个维度上达到最优平衡。全连接层在这个架构中主要承担特征聚合和权重生成的功能，它将输入特征的全局信息转换为各个模块所需的调制参数。整个架构的设计体现了从粗粒度到细粒度的渐进式优化思想：先通过FDW确保权重的基本频率多样性，再通过KSM和FBM进行精细化调整，最终实现既高效又灵活的动态卷积操作。

Dynamic convolution methods [ 63 , 73 ] learn multiple parallel weights and adaptively mix them linearly using attention modules. CondConv [ 73 ] uses a sigmoid function for weight fusion, while DY-Conv improves upon this by using a softmax function [ 63 ]. Inspired by SE [ 26 ], WeightNet [ 50 ], CGC [ 43 ], and WE [ 56 ], these methods design various attention modules to adjust convolutional weights in ConvNets. ODConv [ 32 ] further enhances the attention module by predicting channel-wise, filter-wise, and spatialwise attention values to adjust the weights.

【翻译】动态卷积方法[ 63 , 73 ]学习多个并行权重，并使用注意力模块自适应地线性混合它们。CondConv [ 73 ]使用sigmoid函数进行权重融合，而DY-Conv通过使用softmax函数对此进行改进[ 63 ]。受SE [ 26 ]、WeightNet [ 50 ]、CGC [ 43 ]和WE [ 56 ]启发，这些方法设计了各种注意力模块来调整ConvNets中的卷积权重。ODConv [ 32 ]通过预测通道级、滤波器级和空间级注意力值来调整权重，进一步增强了注意力模块。

【解析】动态卷积是通过学习多个并行的权重分支来提升模型的表达能力和适应性。传统的卷积操作使用固定的权重参数，而动态卷积通过引入多个权重候选并根据输入内容自适应地选择和组合这些权重。这种线性混合策略的数学基础是加权平均，其中注意力模块负责生成归一化的权重系数。CondConv作为早期的代表性工作，采用sigmoid激活函数来生成权重系数，但sigmoid函数的输出不具备归一化特性，这可能导致权重组合时的不稳定性。DY-Conv的改进在于使用softmax函数，它能够确保所有权重系数的和为1，从而提供了更稳定的权重组合机制。注意力模块的设计灵感来源于通道注意力机制，如SE模块通过全局平均池化来聚合空间信息，然后通过两个全连接层来学习通道间的相互依赖关系。WeightNet、CGC和WE等方法在此基础上进一步扩展了注意力机制的设计空间，探索了不同的特征聚合和权重生成策略。ODConv将注意力机制从简单的全局权重扩展到多维度的精细化控制：通道级注意力允许模型为不同的特征通道分配不同的重要性，滤波器级注意力使模型能够选择性地激活不同的卷积核，而空间级注意力则提供了位置相关的权重调节能力。这种多维度的注意力设计大大提升了动态卷积的灵活性和表达能力。

To mitigate the increased parameter overhead of mul- tiple weights, methods like DCD [ 37 ] and PEDConv [ 24 ] use matrix decomposition techniques to construct low-rank weight matrices, reducing computational complexity. More recently, KW [ 31 ] introduced a decomposition approach where kernel weights are divided into smaller, shareable units across different stages and layers, enabling dynamic kernel reconstruction with fewer parameters.

【翻译】为了减轻多个权重增加的参数开销，诸如DCD [ 37 ]和PEDConv [ 24 ]等方法使用矩阵分解技术来构建低秩权重矩阵，降低计算复杂度。最近，KW [ 31 ]引入了一种分解方法，将核权重分解为更小的、可在不同阶段和层间共享的单元，使得能够用更少的参数进行动态核重构。

【解析】参数开销问题是动态卷积面临的主要挑战之一，因为维护多个并行权重分支必然导致参数量的倍数增长。矩阵分解技术为解决这一问题提供了数学理论基础，其核心思想是利用权重矩阵的低秩特性来实现参数压缩。在线性代数中，任何矩阵都可以通过奇异值分解（SVD）表示为几个低秩矩阵的乘积，而卷积权重矩阵通常具有一定的冗余性，这说明它们可以用更紧凑的低秩表示来近似。DCD和PEDConv方法将原始的高维权重矩阵分解为多个较小维度矩阵的乘积形式，例如将一个$k\times k\times C_{in}\times C_{out}$的卷积核分解为几个更小的矩阵，通过控制分解后矩阵的秩来实现参数数量的显著减少。这种分解不仅减少了存储需求，还降低了计算复杂度，因为矩阵乘法的计算量与矩阵维度的乘积成正比。KW方法进一步扩展了这一思路，它不仅在单个层内进行权重分解，还在不同网络层和不同处理阶段之间共享分解得到的基础权重单元。这种跨层共享策略基于一个重要观察：不同层的卷积权重往往具有相似的基础模式，因此可以通过共享这些基础单元并通过不同的组合方式来构造各层的特定权重。动态核重构机制允许模型根据当前输入和任务需求，灵活地组合这些共享的基础单元来生成所需的卷积核，从而在保持表达能力的同时大幅降低参数开销。

In contrast, our FDConv addresses the heavy parameter cost and limited diversity of weights from the frequency aspect, offering a new solution.

【翻译】相比之下，我们的FDConv从频率角度解决了沉重的参数成本和权重多样性有限的问题，提供了一个新的解决方案。

Frequency Domain Learning. Frequency-domain analysis has long been a cornerstone of signal processing [ 15 , 54 ]. Recently, these techniques have been leveraged in deep learning, influencing model optimization strategies [ 75 ], robustness [ 49 ], and generalization abilities [ 65 ] in Deep Neural Networks (DNNs). Moreover, the integration of frequency-domain methods into DNNs has proven effective for learning global features [ 9 , 19 , 27 , 39 , 58 ] and enhancing domain-generalizable representations [ 40 ]. FcaNet [ 55 ] demonstrates that frequency information benefits feature recalibration, while FreqFusion [ 2 ] shows its advantages in feature fusion. Some studies [ 6 , 16 , 17 ] have improved downsampling operations by addressing high-frequency components that lead to aliasing. FADC [ 7 ] enhances dilated convolution by adjusting dilation based on the frequency characteristics of the features. Our method incorporates a frequency-based perspective into dynamic convolution, improving its ability to learn diversified weights for capturing a wider range of frequency information.

【翻译】频域学习。频域分析长期以来一直是信号处理的基石[ 15 , 54 ]。最近，这些技术已被用于深度学习，影响深度神经网络（DNNs）中的模型优化策略[ 75 ]、鲁棒性[ 49 ]和泛化能力[ 65 ]。此外，将频域方法集成到DNNs中已被证明对学习全局特征[ 9 , 19 , 27 , 39 , 58 ]和增强域泛化表示[ 40 ]是有效的。FcaNet [ 55 ]证明了频率信息有利于特征重标定，而FreqFusion [ 2 ]显示了其在特征融合中的优势。一些研究[ 6 , 16 , 17 ]通过解决导致混叠的高频成分来改进下采样操作。FADC [ 7 ]通过根据特征的频率特性调整膨胀来增强膨胀卷积。我们的方法将基于频率的视角纳入动态卷积，提高其学习多样化权重以捕获更广泛频率信息的能力。

【解析】在传统信号处理中，频域分析通过傅里叶变换将时域或空域信号转换到频域，从而揭示信号在不同频率成分上的分布特性，这种分析方式在滤波、去噪、压缩等任务中具有天然的优势。近年来，研究者们逐渐认识到深度神经网络的学习过程本质上也可以从频域角度进行理解和优化。模型优化策略的频域视角主要体现在梯度更新和权重演化的频率特性分析上，通过控制不同频率成分的学习速度可以改善收敛性能；鲁棒性方面的改进则源于频域中对抗样本往往集中在特定频段，通过频域滤波可以有效提升模型的抗攻击能力；泛化能力的提升则基于不同频率成分对泛化的贡献差异，低频信息通常包含更多的泛化相关特征。全局特征学习是频域方法的另一个重要优势，因为傅里叶变换具有全局感受野的特性，能够捕获长距离的空间依赖关系。FcaNet通过在通道注意力机制中引入频率分析，发现不同频率成分对特征重标定的贡献存在显著差异；FreqFusion则利用频域的线性叠加性质来实现更有效的特征融合。下采样中的混叠问题是频域分析的经典应用场景，高频成分在采样不足时会折叠到低频区域造成混叠，通过适当的频域预处理可以有效缓解这一问题。FADC方法展示了频域分析在卷积结构设计中的应用潜力，通过分析特征的频率分布来自适应调整膨胀率，实现了更智能的感受野控制。FDConv将这一频域设计思想引入动态卷积，通过直接在频域中设计和控制权重的频率特性，实现了权重多样性和参数效率的统一优化。

3. Method

An overview of the proposed Frequency Dynamic Convolution (FDConv) framework is shown in Figure 2 . This section first introduces the concept of Fourier Disjoint Weights, followed by a detailed exploration of two key strategies: Kernel Spatial Modulation and Frequency Band Modulation, which are designed to fully leverage the frequency adaptability of FDConv in the kernel spatial and frequency domains, respectively.

【翻译】所提出的频率动态卷积（FDConv）框架概述如图2所示。本节首先介绍傅里叶不相交权重的概念，然后详细探讨两个关键策略：核空间调制和频带调制，它们分别设计用于充分利用FDConv在核空间和频率域中的频率适应性。

3.1. 傅里叶不相交权重

Dynamic Convolution. For a standard convolutional layer, it can be formulated as $\mathbf{Y}=\mathbf{W}\ast \mathbf{X}$, where $\mathbf{X}\in {\mathbb{R}}^{h\times w\times C_{\text{in}}}$ and $\mathbf{Y}\in {\mathbb{R}}^{h\times w\times C_{\text{out}}}$ and are $C_{\text{in}}$ and $C_{\text{out}}$ represent the number of input and output features, $h\times w$ denotes the spatial convolutional filters, each with a spatial size of $k\times k$. The weight $\mathbf{W}\in {\mathbb{R}}^{k\times k\times C_{\text{in}}\times C_{\text{out}}}$.

【翻译】动态卷积。对于标准卷积层，可以公式化为$\mathbf{Y}=\mathbf{W}\ast \mathbf{X}$，其中$\mathbf{X}\in {\mathbb{R}}^{h\times w\times C_{\text{in}}}$和$\mathbf{Y}\in {\mathbb{R}}^{h\times w\times C_{\text{out}}}$，$C_{\text{in}}$和$C_{\text{out}}$分别表示输入和输出特征的数量，$h\times w$表示空间卷积滤波器，每个滤波器的空间大小为$k\times k$。权重$\mathbf{W}\in {\mathbb{R}}^{k\times k\times C_{\text{in}}\times C_{\text{out}}}$。

【解析】标准卷积的数学表达式$\mathbf{Y}=\mathbf{W}\ast \mathbf{X}$中，星号表示卷积运算。输入张量$\mathbf{X}$的维度定义：$h\times w$是特征图的空间尺寸，$C_{\text{in}}$是输入通道数。同样，输出张量$\mathbf{Y}$保持相同的空间尺寸但通道数变为$C_{\text{out}}$。权重张量$\mathbf{W}$的维度$k\times k\times C_{\text{in}}\times C_{\text{out}}$反映了卷积核的完整结构：前两个维度$k\times k$定义了卷积核的空间感受野大小，第三个维度$C_{\text{in}}$确保卷积核能够处理所有输入通道，第四个维度$C_{\text{out}}$表示该层包含多少个不同的卷积核，每个核产生一个输出通道。这种标准卷积的权重在训练完成后是固定的，不会根据输入内容的变化而调整，这限制了模型的适应性和表达能力。

Dynamic convolution [63, 73] enhances the adaptability of convolutional layers by replacing the static weight $\mathbf{W}$ in standard convolution with a combination of $n$ kernels. The contribution of each kernel is modulated by a distinct set of weights {W1,…,Wn}\{\mathbf{W}_1, \dots, \mathbf{W}_n\}{W1​,…,Wn​}, each of the same dimension, dynamically generated. Typically, these coefficients are derived as a set of attention-based coefficients {π1,…,πn}\{\pi_1, \dots, \pi_n\}{π1​,…,πn​}, which are obtained by applying global average pooling on the input, followed by a fully connected (FC) layer. This dynamic convolution operation can be expressed as

【翻译】动态卷积[63, 73]通过用$n$个核的组合替换标准卷积中的静态权重$\mathbf{W}$来增强卷积层的适应性。每个核的贡献由一组不同的权重{W1,…,Wn}\{\mathbf{W}_1, \dots, \mathbf{W}_n\}{W1​,…,Wn​}调制，每个权重具有相同的维度，动态生成。通常，这些系数被推导为一组基于注意力的系数{π1,…,πn}\{\pi_1, \dots, \pi_n\}{π1​,…,πn​}，通过对输入应用全局平均池化，然后应用全连接（FC）层获得。这种动态卷积操作可以表示为

【解析】动态卷积的创新在于摆脱了传统卷积中权重固定不变的限制。传统卷积使用单一的权重矩阵$\mathbf{W}$，而动态卷积维护了$n$个并行的权重矩阵{W1,…,Wn}\{\mathbf{W}_1, \dots, \mathbf{W}_n\}{W1​,…,Wn​}，每个权重矩阵都具有与标准卷积相同的维度。动态性体现在根据当前输入内容自适应地组合这些权重的能力上。注意力机制在这里发挥了关键作用：通过全局平均池化操作，网络能够从输入特征图中提取全局统计信息，这个操作将空间维度$h\times w$的特征图压缩为每个通道的标量值。随后的全连接层学习如何将这些全局特征转换为权重组合系数{π1,…,πn}\{\pi_1, \dots, \pi_n\}{π1​,…,πn​}。这些系数本质上是一种软注意力权重，它们决定了在处理当前输入时，每个并行权重分支应该贡献多少。全连接层的设计使得网络能够学习复杂的映射关系，从输入的全局特征到权重组合策略。这种设计的优势在于它为网络提供了根据输入内容动态调整处理策略的能力，从而提高了模型的表达能力和适应性。

$$\mathbf{W}={\pi }_1{\mathbf{W}}_1+\dots +{\pi }_n{\mathbf{W}}_n.$$

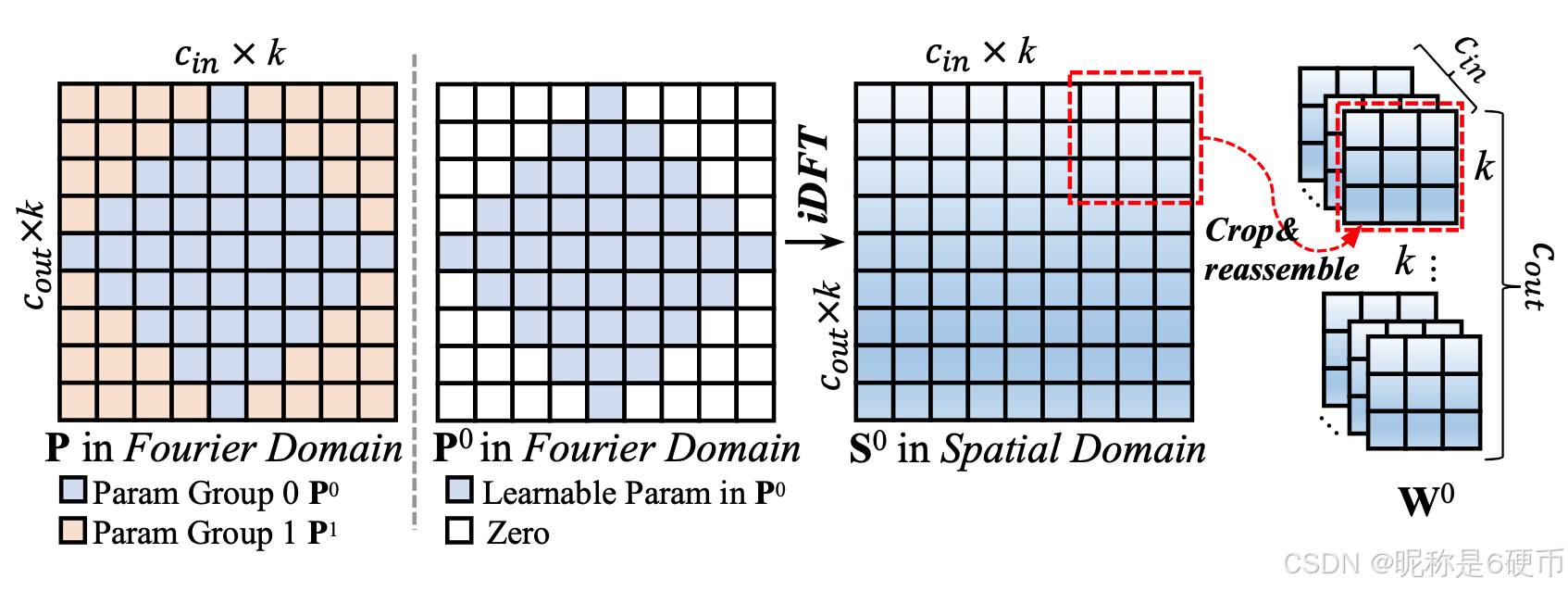
Figure 3. Illustration of Fourier Disjoint Weight ($\mathrm{FDW}$).
The left figure illustrates the division of parameters into disjoint groups, ranging from low frequencies (center) to high frequencies (border). In this example, $n=2$ groups are shown.
The right figure demonstrates how to obtain the convolution weights from the learnable parameter group 0. It first transforms the learnable parameters with specific Fourier indices (with all other Fourier indices set to zero) using the inverse Discrete Fourier Transform ($\mathrm{iDFT}$). The resulting spatial weights are then obtained by cropping the $\mathrm{iDFT}$ result into $k\times k$ patches and reshaping them into a weight tensor of size $k\times k\times C_{\text{in}}\times C_{\text{out}}$.

【翻译】图3. 傅里叶不相交权重（$\mathrm{FDW}$）的说明。左图说明了参数分为不相交组的情况，从低频（中心）到高频（边界）。在这个例子中，显示了$n=2$组。右图演示了如何从可学习参数组0获得卷积权重。它首先使用逆离散傅里叶变换（$\mathrm{iDFT}$）转换具有特定傅里叶索引的可学习参数（将所有其他傅里叶索引设置为零）。然后通过将$\mathrm{iDFT}$结果裁剪为$k\times k$补丁并将其重塑为大小为$k\times k\times C_{\text{in}}\times C_{\text{out}}$的权重张量来获得最终的空间权重。

【解析】图3展示了FDW方法的原理。左侧图形展现了频域参数分组的空间布局，这种布局遵循了傅里叶变换的基本特性：低频成分通常位于频域的中心区域，而高频成分则分布在边缘区域。这种空间排列反映了自然信号和图像的频谱分布规律。将参数按频率范围进行不相交分组的目的是确保每个权重组只负责处理特定频带的信息，从而避免不同频带之间的干扰和重叠。右侧图形详细说明了从频域参数到空间域卷积权重的转换过程。这个过程的关键在于逆离散傅里叶变换（$\mathrm{iDFT}$），它能够将频域中的系数转换回空间域的权重值。在这个转换过程中，只有属于特定组的傅里叶索引对应的参数会被保留，其他位置的参数被设置为零，这确保了生成的空间域权重只包含该组对应的频率成分。最终的权重张量通过裁剪和重塑操作形成标准的卷积核格式，维度为$k\times k\times C_{\text{in}}\times C_{\text{out}}$，这样就可以直接用于卷积运算。这种设计巧妙地实现了在不增加参数总量的前提下生成具有不同频率特性的多个权重。

Despite the increased parameter cost by a factor of $n$ , we expect dynamic convolution to learn diverse weights. However, our analysis reveals, as shown in Figure 1 , that the frequency responses of parallel weights are highly similar. This lack of frequency diversity limits the model’s ability to adaptively capture features across different frequency bands, reducing the flexibility of dynamic convolution.

【翻译】尽管参数成本增加了$n$倍，我们期望动态卷积能学习到多样化的权重。然而，我们的分析表明，如图1所示，并行权重的频率响应高度相似。这种频率多样性的缺乏限制了模型自适应地捕获不同频带特征的能力，降低了动态卷积的灵活性。

【解析】通过频域分析发现，看似独立的权重在频率响应上表现出惊人的相似性。频率响应描述了滤波器对不同频率成分的敏感程度，相似的频率响应说明这些权重本质上在做相似的特征提取工作，这就违背了动态卷积设计的初衷。这种频率多样性的缺失产生了严重的后果：模型无法有效地在不同频带上进行自适应特征捕获。在计算机视觉任务中，不同频带的信息承载着不同的语义内容，低频信息通常包含全局结构和主要形状，而高频信息则包含细节、纹理和边缘。如果所有权重都只关注相似的频带，模型就失去了全频谱特征提取的能力，这直接削弱了动态卷积相对于静态卷积的优势。

Overview of Fourier Disjoint Weight. To construct multiple parallel weights with high frequency response diversity without increasing parameter costs, we propose Fourier Disjoint Weight (FDW). Unlike previous methods [ 32 , 63 , 73 ], which are limited to a small number of kernels $(n<10)$ ) due to high parameter costs, FDW can generate $n>10$ diversified weights.

【翻译】傅里叶不相交权重概述。为了在不增加参数成本的情况下构建具有高频率响应多样性的多个并行权重，我们提出了傅里叶不相交权重（FDW）。与之前的方法[32, 63, 73]不同，这些方法由于高参数成本而限制于少数内核$(n<10)$，FDW可以生成$n>10$个多样化权重。

【解析】概括了FDW方法的优势。传统动态卷积方法面临一个根本性的权衡问题：要获得更多样化的权重就必须增加参数数量，而参数数量的增长会带来计算和存储的巨大开销。这种线性关系使得以往的方法在实际应用中只能维持相对较少的并行权重数量，通常$n<10$。FDW的创新之处在于打破了这种线性关系，它通过在频域中设计权重生成机制，实现了参数效率和权重多样性的双重优化。FDW的工作原理基于一个重要观察：不同的权重可以通过控制其频域表示来获得不同的频率特性，而这种控制不需要成比例地增加参数数量。通过将有限的参数按照频率进行不相交划分，每个权重组只负责特定的频带，从而自然地保证了权重之间的频率多样性。这种设计使得FDW能够生成$n>10$个具有明显不同频率特性的权重，而参数总量保持不变。这不仅解决了参数效率问题，更重要的是为模型提供了更细粒度的频率控制能力，使得动态卷积能够真正实现跨频谱的自适应特征提取。

The core concept of FDW is learning spectral coefficients in the Fourier domain with disjoint sets of Fourier indices, rather than in the traditional spatial domain. FDW involves three steps to construct $n$ weights: 1) Fourier disjoint grouping. Divide a fixed number of parameters into $n$ groups with disjoint Fourier indices. 2) Fourier to spatial transformation. Convert each group of parameters from the Fourier domain to the spatial domain using the Inverse Discrete Fourier Transform (iDFT). 3) Reassembling. Crop the transformed results in the spatial domain into $k\times k$ patches and reassemble them into the standard weight shape of $k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$ .

【翻译】FDW的核心概念是在傅里叶域中使用不相交的傅里叶索引集合学习频谱系数，而不是在传统的空间域中。FDW涉及三个步骤来构造$n$个权重：1) 傅里叶不相交分组。将固定数量的参数分为具有不相交傅里叶索引的$n$组。2) 傅里叶到空间变换。使用逆离散傅里叶变换（iDFT）将每组参数从傅里叶域转换到空间域。3) 重新组装。将空间域中转换后的结果裁剪成$k\times k$补丁，并将其重新组装成标准权重形状$k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$。

【解析】傅里叶域中的每个位置对应特定的频率成分，通过控制不同位置的系数，可以精确地设计权重的频率特性。三步骤构造过程形成了一个完整的权重生成流水线。第一步傅里叶不相交分组是整个方法的基础，它确保了不同权重组在频率上的分离性。不相交的含义是每个傅里叶索引只属于一个组，这样避免了频率重叠，保证了权重之间的频率多样性。第二步傅里叶到空间变换通过iDFT将频域设计转换为可以实际使用的空间域权重。这个变换过程是数学上严格的，确保了频域设计能够准确地反映在最终的卷积操作中。第三步重新组装处理了维度匹配问题，将变换后的结果整理成标准卷积核的格式。这个三步流程的设计巧妙之处在于它将频率控制（第一步）、数学变换（第二步）和实际应用（第三步）有机结合，既保持了方法的理论严谨性，又确保了实际应用的可行性。通过这种设计，FDW能够生成具有明确频率特性差异的多个权重，为后续的动态组合提供了高质量的基础组件。

Fourier Disjoint Grouping. Given a parameter budget of $k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$ , FDW first treats these parameters as learnable spectral coefficients in the Fourier domain, reshaping them into $\mathbf{P}\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$ . Each parameter is associated with a Fourier index $(u,v)$ , i.e ., coordinates in the Fourier domain that indicate frequency. FDW then sorts these parameters from low to high frequency based on the $L_2$ norm of the Fourie index, $||(u,v)|{|}_2$, and divides them uniformly into disjoint n set, {P0,…,Pn−1}\{\mathbf{P}^{0},\ldots,\mathbf{P}^{n-1}\}{P0,…,Pn−1} .

【翻译】傅里叶不相交分组。给定参数预算$k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$，FDW首先将这些参数视为傅里叶域中的可学习频谱系数，将其重塑为$\mathbf{P}\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$。每个参数都与傅里叶索引$(u,v)$相关联，即傅里叶域中指示频率的坐标。然后FDW根据傅里叶索引的$L_2$范数$||(u,v)|{|}_2$将这些参数从低频到高频排序，并将其均匀地分为不相交的n个集合{P0,…,Pn−1}\{\mathbf{P}^{0},\ldots,\mathbf{P}^{n-1}\}{P0,…,Pn−1}。

【解析】傅里叶不相交分组的实现细节。首先，总的参数量保持为$k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$，与标准卷积相同。重塑操作将四维权重张量转换为二维矩阵$\mathbf{P}\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$，这种重塑不仅是为了计算便利，更重要的是为每个参数建立了与傅里叶域坐标的一一对应关系。傅里叶索引$(u,v)$不仅仅是数学上的坐标，它们具有明确的物理含义：距离原点越远的索引对应越高的频率成分。$L_2$范数$||(u,v)|{|}_2=\sqrt{u^2+v^2}$提供了一个自然的频率排序标准，它计算每个索引到傅里叶域原点的欧几里得距离。这个距离直接反映了对应频率成分的频率高低，距离越小频率越低，距离越大频率越高。基于这个排序进行的均匀分组确保了每个组包含相似数量的参数，同时保持了频率范围的连续性。不相交性保证了每个参数只属于一个组，这是实现频率多样性的关键。最终得到的$n$个参数集合{P0,…,Pn−1}\{\mathbf{P}^{0},\ldots,\mathbf{P}^{n-1}\}{P0,…,Pn−1}按照频率从低到高排列，每个集合负责特定的频率范围，为后续生成具有不同频率特性的权重奠定了基础。这种分组策略的优势在于它将频率控制问题转化为简单的参数分配问题，既保持了数学上的严格性，又具有很强的可操作性。

As shown on the left side of Figure 3 , we divide the learnable parameters into $n=2$ groups for simplicity in the demonstration, where the center represents low frequencies and the border represents high frequencies. Moreover, the number of groups, $n$ , can be set to a large value $(n>10)$ , allowing for the generation of a large number of diversified weights without increasing the parameter cost.

【翻译】如图3左侧所示，为了演示的简单性，我们将可学习参数分为$n=2$组，其中中心代表低频，边界代表高频。此外，组数$n$可以设置为大值$(n>10)$，允许在不增加参数成本的情况下生成大量多样化的权重。

【解析】FDW方法的空间分布策略。在频域中，频率的空间分布遵循特定的规律：低频成分集中在频谱的中心区域，而高频成分则分布在频谱的边缘区域。这种分布模式源于傅里叶变换的数学性质，其中距离频域原点的距离直接对应于频率的大小。将参数按照这种空间分布进行分组不仅具有数学上的合理性，更重要的是能够确保每个组处理特定的频率范围。当$n=2$时，一个组主要负责低频信息的处理，另一个组专注于高频细节的捕获。这种分组方式的优势在于其可扩展性：$n$值可以设置得很大，甚至超过10，而不会带来参数量的线性增长。这种参数效率来源于FDW的核心设计思想：通过控制频域中参数的分布而非简单地复制参数来实现权重的多样化。每增加一个组，只是重新分配现有参数在频域中的使用权，而不是增加新的参数。这种设计使得FDW能够生成数量远超传统动态卷积方法的多样化权重，为模型提供更细粒度的频率控制能力。

Fourier to Spatial Transformation. To obtain the weights, FDW transforms each group of parameters into the spatial domain using the inverse Discrete Fourier Transform (iDFT). This can be formulated as:

【翻译】傅里叶到空间变换。为了获得权重，FDW使用逆离散傅里叶变换（iDFT）将每组参数转换到空间域。这可以公式化为：

【解析】傅里叶到空间变换是FDW方法的核心数学操作。这个步骤的目的是将在频域中设计和分组的参数转换为可以直接用于卷积运算的空间域权重。逆离散傅里叶变换（iDFT）是这个转换过程的数学基础，它能够将频域中的复数系数转换为空间域中的实数权重值。这个变换过程的重要性在于它建立了频域设计与空间域应用之间的桥梁。通过iDFT，我们能够精确地控制生成的空间域权重具有特定的频率特性，这些特性正是在频域分组阶段所设计的。变换的数学严谨性保证了频域中的每个设计决策都能准确地反映在最终的空间域权重中，从而实现了从频率控制到实际卷积操作的无缝转换。

$${\mathbf{S}}_{p,q}^i=\sum _{u=0}^{k{C}_{\mathrm{in}}-1}\sum _{v=0}^{k{C}_{\mathrm{out}}-1}{\mathbf{P}}_{u,v}^i{e}^{i2\pi \left(\frac{p}{k{C}_{\mathrm{in}}}u+\frac{q}{k{C}_{\mathrm{out}}}v\right)}$$

where ${\mathbf{P}}_{u,v}^i$ is the parameter with Fourier index $(u,v)$ in the $i$ -th group ${\mathbf{P}}^i$ . As shown on the right side of Figure 3 , if the Fourier index $(u,v)$ is assigned to the $i$-th group, then ${\mathbf{P}}_{u,v}^i={\mathbf{P}}_{u,v}$ , otherwise, ${\mathbf{P}}_{u,v}^i=0$ . ${\mathbf{S}}_{p,q}^i\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$ represents the element at position $(p,q)$ in the converted results in the spatial domain.

【翻译】其中${\mathbf{P}}_{u,v}^i$是第$i$组${\mathbf{P}}^i$中具有傅里叶索引$(u,v)$的参数。如图3右侧所示，如果傅里叶索引$(u,v)$被分配给第$i$组，则${\mathbf{P}}_{u,v}^i={\mathbf{P}}_{u,v}$，否则，${\mathbf{P}}_{u,v}^i=0$。${\mathbf{S}}_{p,q}^i\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$表示空间域转换结果中位置$(p,q)$处的元素。

【解析】这个数学公式详细描述了iDFT变换的具体实现过程。公式中的双重求和结构反映了二维傅里叶变换的本质：它需要遍历所有可能的频域坐标$(u,v)$。参数${\mathbf{P}}_{u,v}^i$的取值规则体现了不相交分组的核心思想。当某个频域坐标$(u,v)$属于第$i$组时，该位置的参数值保持原始值${\mathbf{P}}_{u,v}$；当该坐标不属于第$i$组时，对应的参数值被设置为零。这种选择性赋值机制确保了每个组只包含特定频率范围的信息，从而实现了频率的不相交分离。指数项$e^{i2\pi \left(\frac{p}{k{C}_{\mathrm{in}}}u+\frac{q}{k{C}_{\mathrm{out}}}v\right)}$是傅里叶变换的核心，它建立了频域坐标$(u,v)$与空间域坐标$(p,q)$之间的数学关系。通过这个变换，频域中的每个参数都会对空间域中的每个位置产生特定的贡献，而这种贡献的模式正是由参数对应的频率决定的。最终得到的${\mathbf{S}}_{p,q}^i$是一个空间域的二维矩阵，它包含了第$i$组频率成分对应的空间域表示，为后续的权重重组步骤提供了基础。

Reassembling. As shown on the right side of Figure 3 , the final $i$-th weight ${\mathbf{W}}^i\in {\mathbb{R}}^{k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}}$ be obtained by cropping ${\mathbf{S}}^i\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$ into $C_{\mathrm{in}}\times C_{\mathrm{out}}$ patches of size $k\times k$ and reassembling them to form ${\mathbf{W}}^i$ .

【翻译】重新组装。如图3右侧所示，最终的第$i$个权重${\mathbf{W}}^i\in {\mathbb{R}}^{k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}}$可以通过将${\mathbf{S}}^i\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$裁剪成$C_{\mathrm{in}}\times C_{\mathrm{out}}$个大小为$k\times k$的补丁并重新组装它们以形成${\mathbf{W}}^i$来获得。

【解析】重新组装步骤是FDW方法的最后一个关键环节，它将经过傅里叶变换得到的空间域结果转换为可以直接用于卷积运算的标准权重格式。这个过程涉及复杂的维度重塑操作。从数学角度来看，经过iDFT变换后得到的${\mathbf{S}}^i\in {\mathbb{R}}^{k{C}_{\mathrm{in}}\times k{C}_{\mathrm{out}}}$是一个二维矩阵，但标准卷积权重需要四维张量${\mathbf{W}}^i\in {\mathbb{R}}^{k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}}$的格式。裁剪和重新组装操作就是要解决这个维度匹配问题。具体来说，二维矩阵${\mathbf{S}}^i$需要被分割成$C_{\mathrm{in}}\times C_{\mathrm{out}}$个小的$k\times k$补丁，每个补丁对应最终四维权重张量中的一个$k\times k$卷积核。这种重新组装不仅仅是简单的维度变换，它确保了频域设计的频率特性能够正确地映射到空间域的卷积操作中。通过这种精心设计的重新组装过程，FDW能够生成既保持特定频率特性又符合标准卷积格式要求的权重张量。

Since the parameters are divided according to frequency, ${\mathbf{S}}^i$ contains only the frequency components of a specific band. Therefore, each weight ${\mathbf{W}}^i$ derived from ${\mathbf{S}}^i$ exhibits a distinct frequency response compared to ${\mathbf{W}}^j$ when $i\ne j$ . This ensures that the frequency responses of the constructed weights are diversified. After a linear mixture, as described in Equation ( 1 ), FDW can adaptively adjust the frequency response of the combined weight based on the input sample.

【翻译】由于参数是根据频率进行分组的，${\mathbf{S}}^i$只包含特定频段的频率成分。因此，从${\mathbf{S}}^i$派生的每个权重${\mathbf{W}}^i$与当$i\ne j$时的${\mathbf{W}}^j$相比，表现出不同的频率响应。这确保了构造权重的频率响应是多样化的。在如方程(1)所述的线性混合之后，FDW可以根据输入样本自适应地调整组合权重的频率响应。

【解析】由于在傅里叶不相交分组阶段，不同组的参数被分配到不同的频率范围，每个变换后的结果${\mathbf{S}}^i$自然地只包含其对应频段的频率成分。这种频段专一性直接转化为生成权重的频率响应差异。当$i\ne j$时，权重${\mathbf{W}}^i$和${\mathbf{W}}^j$由于来源于不同的频率组，它们的频率响应特性必然存在显著差异。这种差异不是偶然的，而是由FDW方法的设计机制保证的。频率响应的多样化为后续的自适应调整提供了坚实的基础。通过方程(1)描述的线性混合机制，模型可以根据输入样本的特征动态地组合这些具有不同频率特性的权重。这种组合过程实质上是在频率域中进行精细调控，使得最终的组合权重能够针对特定输入展现出最适合的频率响应模式。这种自适应能力是FDW方法相对于传统静态卷积的核心优势，它使得模型能够根据输入内容的频率特征动态调整其处理策略。

Note that FDW can also be applied to linear layers in modern vision architectures, such as Transformers [ 12 , 46 ], which are equivalent to convolutions with a kernel size of 1.

【翻译】注意，FDW也可以应用于现代视觉架构中的线性层，如Transformers [12, 46]，这等价于核大小为1的卷积。

【解析】从数学角度来看，线性层实际上可以被视为一种特殊的卷积操作，即核大小为$1\times 1$的卷积。这种等价性为FDW方法的应用提供了更广阔的空间。在Transformer架构中，多头注意力机制和前馈网络都大量使用线性层进行特征变换。通过将FDW应用于这些线性层，可以为Transformer模型引入频率域的自适应能力。虽然$1\times 1$卷积在空间维度上没有邻域感受野，但在频率域中仍然具有明确的频率响应特性。FDW可以让这些线性层根据输入的频率特征进行自适应调整，这对于处理视觉任务中的多尺度和多频率信息尤为重要。

3.2. 核空间调制

By ensuring the diversity of frequency responses of parallel weights in the Fourier domain, FDW can adaptively adjust the frequency response of the combined weight based on the input sample after a linear mixture, as described in Equation ( 1 ). However, this weight-wise mixture is too coarse and cannot independently adjust the frequency response of each $k\times k$ filter in the weight.

【翻译】通过确保傅里叶域中并行权重的频率响应多样性，FDW可以在如方程(1)所述的线性混合后，根据输入样本自适应地调整组合权重的频率响应。然而，这种权重级别的混合过于粗糙，无法独立调整权重中每个$k\times k$滤波器的频率响应。

【解析】尽管FDW方法通过傅里叶域设计实现了不同权重之间的频率多样性，但其混合机制存在粒度上的局限性。FDW的线性混合是在整个权重张量层面进行的，这说明所有的$k\times k$滤波器核都使用相同的混合系数。这种"一刀切"的混合策略虽然能够在全局层面调整频率响应，但无法针对权重张量内部的不同滤波器进行细粒度的个性化调整。在实际的特征提取过程中，不同的滤波器往往需要处理不同类型的特征模式，因此它们对频率响应的需求也不尽相同。有些滤波器可能需要更多的低频成分来捕获整体结构，而另一些滤波器则需要更多的高频成分来检测细节边缘。权重级别的混合无法满足这种多样化的需求，这就限制了模型的表达能力和适应性。这个问题的根源在于混合操作的空间尺度与实际需求之间的不匹配，需要一种更加精细化的调制机制来解决。

To address this issue, we propose Kernel Spatial Modulation (KSM), which predicts a dense modulation matrix $\alpha \in {\mathbb{R}}^{k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}}$ , instead of a sparse vector. As shown in Figure 4 , KSM consists of a local channel branch and a global channel branch.

【翻译】为了解决这个问题，我们提出了核空间调制（KSM），它预测一个密集调制矩阵$\alpha \in {\mathbb{R}}^{k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}}$，而不是稀疏向量。如图4所示，KSM由局部通道分支和全局通道分支组成。

【解析】KSM方法的核心创新在于从稀疏调制向密集调制的转变。传统的动态卷积方法通常使用稀疏向量进行权重调制，这种稀疏性体现在调制系数的数量远少于权重参数的总数。而KSM预测的密集调制矩阵$\alpha \in {\mathbb{R}}^{k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}}$与权重张量具有完全相同的维度结构，这说明每个权重参数都有对应的调制系数。这种一对一的对应关系使得KSM能够实现真正的元素级精细调制。双分支架构的设计体现了信息处理的层次性考虑：局部通道分支专注于捕获局部特征相关性，而全局通道分支则负责整合全局上下文信息。这种分工合作的架构设计既保证了调制的精细度，又确保了全局信息的有效利用。

Local Channel Branch. While global fully connected layers are commonly used for modulation value prediction [ 26 , 32 , 63 , 73 ], they are not suitable for predicting dense modulation matrices due to their large parameter and computational costs. To address this, the local channel branch employs a lightweight 1-D convolution, which has been proven to be efficient and effective [ 67 ]. It captures local channel information and predicts a dense modulation matrix of size $k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$ . This approach significantly reduces parameters and computational complexity while maintaining the ability to learn fine-grained modulation for each element in the weight.

【翻译】局部通道分支。虽然全局全连接层通常用于调制值预测[26, 32, 63, 73]，但由于其巨大的参数和计算成本，它们不适合预测密集调制矩阵。为了解决这个问题，局部通道分支采用了轻量级的1-D卷积，这已被证明是高效且有效的[67]。它捕获局部通道信息并预测大小为$k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$的密集调制矩阵。这种方法显著减少了参数和计算复杂度，同时保持了为权重中每个元素学习细粒度调制的能力。

【解析】传统的全连接层虽然能够建立任意输入与输出之间的映射关系，但当需要预测与权重张量同等规模的密集调制矩阵时，其参数量会急剧增长。具体来说，如果输入特征维度为$d$，需要预测的调制矩阵大小为$k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$，那么全连接层的参数量将达到$d\times k^2\times C_{\mathrm{in}}\times C_{\mathrm{out}}$，这在现代深度网络中是不可接受的。1-D卷积的引入巧妙地解决了这个问题。1-D卷积能够捕获通道维度上的局部相关性，这种局部性假设在实践中是合理的，因为相邻通道往往具有相似的语义含义。通过在通道维度上进行卷积操作，局部通道分支能够以远低于全连接层的参数开销生成所需的密集调制矩阵。这种设计的有效性在于它保持了调制的精细粒度，每个权重元素都有独立的调制系数，从而实现了真正的元素级自适应调整。

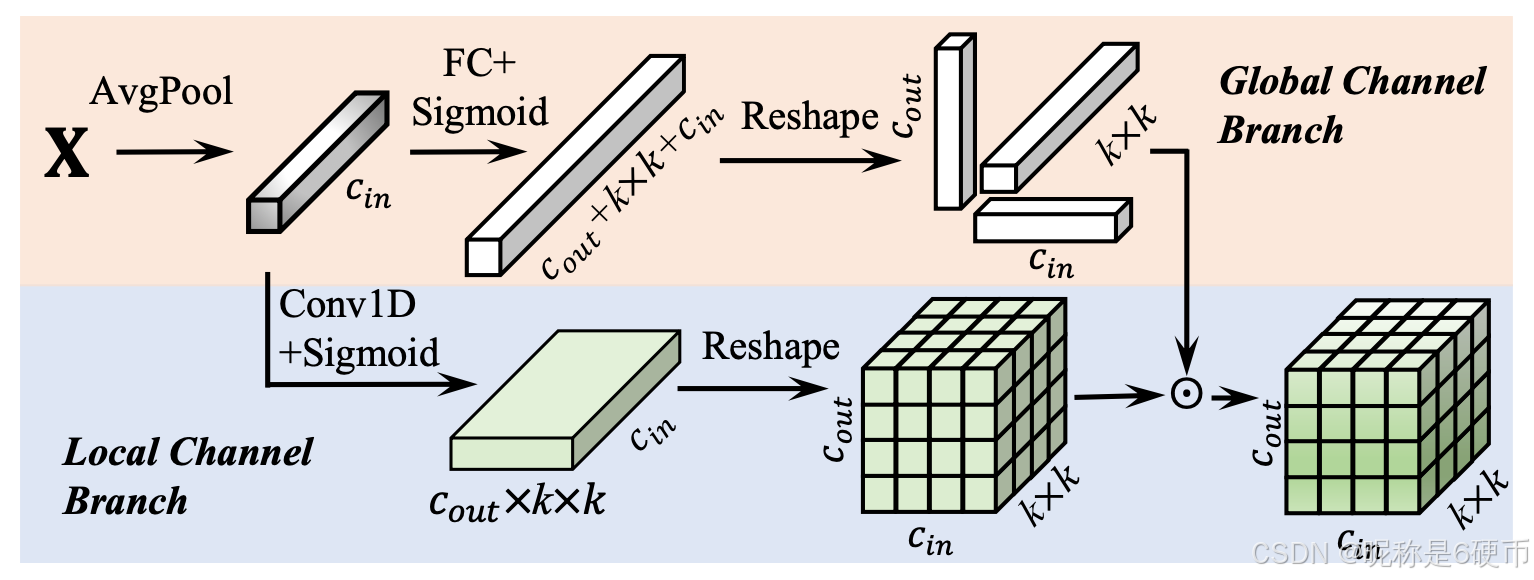
Figure 4. Illustration of Kernel Spatial Modulation (KSM). The KSM consists of two branches: the global channel branch and the local channel branch. The local channel branch employs a very lightweight 1-D convolution to obtain local channel information predicts a dense modulation matrix of size $k\times k\times C_{\mathrm{in}}\times$ $C_{\mathrm{out}}$ . The global branch uses a fully connected layer to obtain the global channel information and predicts three dimension-wise modulation values along the input channel, output channel, and kernel spatial dimensions. The two branches are fused to obtain the final weight modulation matrix.

【翻译】图4. 核空间调制（KSM）的示意图。KSM由两个分支组成：全局通道分支和局部通道分支。局部通道分支采用非常轻量级的1-D卷积来获取局部通道信息，预测大小为$k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$的密集调制矩阵。全局分支使用全连接层来获取全局通道信息，并沿输入通道、输出通道和核空间维度预测三个维度级的调制值。两个分支融合以获得最终的权重调制矩阵。

【解析】图4展示了KSM的双分支架构设计。局部通道分支和全局通道分支体现了信息处理的层次性原则。局部分支通过1-D卷积捕获通道间的局部相关性，这种设计基于相邻通道往往具有相似语义特征的假设。该分支生成的密集调制矩阵$k\times k\times C_{\mathrm{in}}\times C_{\mathrm{out}}$与权重张量维度完全匹配，实现了元素级的精细调制。全局分支则采用全连接层进行全局信息整合，但为了控制参数开销，它只预测三个维度级的调制值：输入通道维度、输出通道维度和核空间维度。这种稀疏调制设计在保持全局感知能力的同时避免了参数爆炸。两个分支的融合过程将局部细粒度调制与全局维度级调制相结合，形成既具有局部适应性又保持全局一致性的最终调制矩阵。

Global Channel Branch. Though the local channel branch can efficiently predict the modulation matrices, it lacks global information, which is crucial for weight adjustments. To complement the local channel branch, the global channel branch uses a fully connected layer to capture global channel information and predict a sparse modulation vector for efficiency. Specifically, it predicts three dimension-wise modulation values: one for the input channel, one for the output channel, and one for the kernel spatial dimensions, ensuring that both local and global contextual information are incorporated for adaptive modulation.

【翻译】全局通道分支。尽管局部通道分支可以高效地预测调制矩阵，但它缺乏对权重调整至关重要的全局信息。为了补充局部通道分支，全局通道分支使用全连接层来捕获全局通道信息，并为了效率预测稀疏调制向量。具体来说，它预测三个维度级的调制值：一个用于输入通道，一个用于输出通道，一个用于核空间维度，确保局部和全局上下文信息都被纳入自适应调制中。

【解析】全局通道分支的设计解决了局部分支的固有局限性。虽然1-D卷积能够捕获局部通道相关性，但由于其感受野限制，无法建立远距离通道之间的依赖关系。这种全局信息的缺失在处理复杂特征模式时可能导致调制策略的不完整。全连接层的引入弥补了这个不足，它能够建立任意两个通道之间的连接，从而捕获全局通道依赖关系。然而，直接预测与权重张量同等规模的密集调制矩阵会导致参数量急剧增长。因此，全局分支采用稀疏调制策略，只预测三个关键维度的调制值。这种维度级调制虽然粒度较粗，但能够有效地进行全局调控。输入通道维度调制控制不同输入特征的重要性，输出通道维度调制调节不同输出特征的激活强度，而核空间维度调制则影响空间邻域信息的整合方式。通过这种分层调制机制，全局分支在保持计算效率的同时提供了必要的全局上下文指导。

In this way, the proposed KSM is able to leverage both local and global information, enabling more precise and context-aware modulation of each filter in the weights.

【翻译】通过这种方式，所提出的KSM能够利用局部和全局信息，使权重中每个滤波器的调制更加精确和上下文感知。

【解析】KSM的双分支融合机制实现了多层次信息的有效整合。局部分支提供的细粒度调制确保了每个权重元素都能根据局部特征相关性进行精确调整，而全局分支提供的维度级调制则保证了整体调制策略的全局一致性和合理性。这种多层次调制的协同作用使得模型能够在保持局部适应性的同时避免调制策略的局部最优陷阱。上下文感知能力的提升体现在模型能够根据输入特征的全局和局部特性动态调整每个滤波器的行为模式，这种调整不仅考虑了当前位置的特征特性，还综合了整个特征图的全局信息分布。因此，KSM实现了从静态权重向动态权重的转变，使卷积操作能够根据具体输入内容进行自适应调整，从而提高了特征提取的精度和效率。

3.3. 频率带调制

While the proposed Fourier Disjoint Weight (FDW) and Kernel Spatial Modulation (KSM) modules substantially enhance adaptability by ensuring frequency diversity and element-wise adjustments, they remain spatially invariant, as is typical in dynamic convolution [ 31 , 32 , 63 , 73 ]. This spatial invariance, where weights are shared across the entire feature map, restricts convolutional layers from dynamically adapting frequency responses to spatially varying content, limiting their ability to fully capture complex structures across the image.

【翻译】虽然所提出的傅里叶不相交权重（FDW）和核空间调制（KSM）模块通过确保频率多样性和元素级调整大大增强了适应性，但它们仍然保持空间不变性，这在动态卷积[31, 32, 63, 73]中是典型的。这种空间不变性，即权重在整个特征图上共享，限制了卷积层根据空间变化内容动态调整频率响应的能力，限制了它们充分捕获图像中复杂结构的能力。

【解析】尽管FDW和KSM在自适应性方面取得了显著进展，但它们都存在设计局限：空间不变性。这种不变性体现在无论输入特征图的哪个空间位置，都使用相同的权重参数进行卷积运算。这种设计遵循了传统卷积的基本假设，即认为图像的统计特性在空间上是平稳的。然而，这种假设在处理复杂自然图像时往往不成立。图像的不同区域可能包含截然不同的内容：例如，前景区域可能充满细节和边缘信息，需要更多的高频成分来精确提取；而背景区域可能相对平滑，需要更多的低频成分来抑制噪声。空间不变的权重无法根据这些局部内容特性进行针对性调整，导致在某些区域过度提取不必要的频率成分，而在另一些区域则可能遗漏关键的频率信息。这种"一刀切"的处理方式限制了模型对图像复杂空间结构的理解和表达能力。

Natural images and their corresponding features exhibit large spatial variation, which necessitates frequencyspecific adaptations for optimal feature extraction. For example, extracting low-frequency components is vital for suppressing feature noise [ 3 ], while high-frequency components are essential for capturing fine details and boundaries [ 2 , 51 ], which are crucial for distinguishing the foreground from the background.

【翻译】自然图像及其对应的特征表现出很大的空间变化，这需要频率特定的适应以实现最佳特征提取。例如，提取低频成分对于抑制特征噪声至关重要[3]，而高频成分对于捕获细节和边界是必需的[2, 51]，这对于区分前景和背景至关重要。

【解析】前景物体通常具有清晰的边界和丰富的纹理细节，这些都体现为高频特征；而背景往往相对平滑，主要由低频成分构成。因此，理想的特征提取方法应该能够根据不同空间位置的内容特性，动态调整对不同频率成分的敏感度，从而实现更加精准和上下文感知的特征提取。

Overview of Frequency Band Modulation. To address the need for spatially dynamic frequency modulation, we propose Frequency Band Modulation (FBM). FBM decomposes the convolutional kernel into multiple frequency bands in the frequency domain and applies spatially specific modulations, adaptively adjusting each frequency component across different spatial locations.

【翻译】频率带调制概述。为了解决空间动态频率调制的需求，我们提出了频率带调制（FBM）。FBM在频率域将卷积核分解为多个频率带，并应用空间特定的调制，在不同空间位置自适应地调整每个频率成分。

【解析】FBM方法设计思路分为两个关键步骤：首先是频率域分解，将单一的卷积核转换为多个频率带特定的子核，每个子核专门负责处理特定频率范围的信息；其次是空间特定调制，为每个频率带在不同空间位置生成独立的调制系数。这种设计使得模型能够根据输入特征图中每个位置的具体内容特性，动态调整对不同频率成分的响应强度。例如，在图像的边缘区域，模型可以增强高频成分的响应来更好地捕获边界信息；而在平滑区域，模型可以增强低频成分的响应来抑制噪声并保持结构完整性。这种精细化的频率调制策略不仅提高了特征提取的精度，还增强了模型对复杂图像结构的理解能力。

The Frequency Band Modulation operates in the following key steps: 1) Kernel frequency decomposition. Decomposing the frequency response of the convolution weight into different frequency bands. 2) Convolution in the Fourier domain. Performing convolution in the Fourier domain. 3) Spatially variant modulation. Predicting modulation values for each frequency band of the convolution weight across different spatial locations.

【翻译】频率带调制按照以下关键步骤操作：1）核频率分解。将卷积权重的频率响应分解为不同的频率带。2）傅里叶域卷积。在傅里叶域中执行卷积。3）空间变化调制。为卷积权重的每个频率带在不同空间位置预测调制值。

【解析】核频率分解步骤将传统的单一卷积核转换为多个频率特化的子核，每个子核专门负责处理特定频率范围的信息，这种分解基于信号处理中的频域分析理论。傅里叶域卷积步骤利用卷积定理，将空间域的卷积转换为频域的逐点乘法，不仅提高了计算效率，还使得频率带的精确分离成为可能。空间变化调制为每个频率带在特征图的每个空间位置生成独立的调制系数，打破了传统卷积的空间不变性约束，使模型能够根据局部内容特性动态调整不同频率成分的重要性。

The core formulation of FBM is given by:

【翻译】FBM的核心公式如下：

$$\mathbf{Y}=\sum _{b=0}^{B-1}({\mathbf{A}}_b\odot ({\mathbf{W}}_b\ast \mathbf{X})),$$

where $\mathbf{X}$ and $\mathbf{Y}\in {\mathbb{R}}^{h\times w}$ are the input and output feature maps. Note that we omit the channel dimension for simplicity. ${\mathbf{A}}_b\in {\mathbb{R}}^{h\times w}$ representing spatial dula on values specific to the b-th frequency band, And ${\mathbf{W}}_b$ the b-th frequency band of weight. FBM enables adjusting the frequency responses for each spatial location of feature map.

【翻译】其中$\mathbf{X}$和$\mathbf{Y}\in {\mathbb{R}}^{h\times w}$是输入和输出特征图。注意为了简化，我们省略了通道维度。${\mathbf{A}}_b\in {\mathbb{R}}^{h\times w}$表示特定于第b个频率带的空间调制值，${\mathbf{W}}_b$是权重的第b个频率带。FBM能够为特征图的每个空间位置调整频率响应。

【解析】公式展现了FBM：将传统的单一卷积操作转换为多个频率特化卷积的加权组合。求和符号${\sum }_{b=0}^{B-1}$表示对所有$B$个频率带的结果进行累加。每个频率带的贡献由两部分组成：首先是${\mathbf{W}}_b\ast \mathbf{X}$，这是第$b$个频率带权重与输入特征图的卷积；然后是${\mathbf{A}}_b\odot$，这是空间调制矩阵与卷积结果的逐元素乘法。调制矩阵${\mathbf{A}}_b$的关键特性在于它具有与特征图相同的空间尺寸，但每个频率带都有独立的调制矩阵，这使得模型能够在每个空间位置独立控制不同频率成分的强度。这种设计实现了真正的空间自适应频率调制，每个位置都可以根据局部内容特性选择性地增强或抑制特定频率成分。

Kernel frequency decomposition. To decompose the convolution kernel into distinct frequency bands, FBM first pads the kernel W to match the feature map size [ 52 ], and then applies a set of binary masks ${\mathcal{M}}_b$ to isolate specific frequency ranges:

$${\mathbf{W}}_b={\mathcal{F}}^{-1}({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{W})),$$

where $\mathcal{F}$ and ${\mathcal{F}}^{-1}$ denote the DFT and inverse DFT, and ${\mathcal{M}}_b$ is a binary mask isolating specific frequency ranges:

$${\mathcal{M}}_b(u,v)=\{\begin{array}{ll}1& \mathrm{if}{\psi }_b\le \max (|u|,|v|)<{\psi }_{b+1}\\ 0& \mathrm{otherwise}\end{array}$$

Here, ${\psi }_b$ and ${\psi }_{b+1}$ are thresholds from the predefined frequency set {0,ψ1,…,ψB−1,12}\{0,\psi_{1},\ldots,\psi_{B-1},\frac{1}{2}\}{0,ψ1​,…,ψB−1​,21​} } , where $(u,v)$ denote the horizontal and vertical frequency indices. By default, we decompose the frequency spectrum into four distinct bands using an octave-based partitioning strategy [ 60 ]. The thresholds for dividing the frequency bands are {0,116,18,14,12}\{0,\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2}\}{0,161​,81​,41​,21​} } .

【翻译】核频率分解。为了将卷积核分解为不同的频率带，FBM首先将核W填充以匹配特征图的大小[52]，然后应用一组二进制掩码${\mathcal{M}}_b$来隔离特定的频率范围。其中$\mathcal{F}$和${\mathcal{F}}^{-1}$表示DFT和逆DFT，${\mathcal{M}}_b$是一个二进制掩码，用于隔离特定的频率范围。这里，${\psi }_b$和${\psi }_{b+1}$是来自预定义频率集合{0,ψ1,…,ψB−1,12}\{0,\psi_{1},\ldots,\psi_{B-1},\frac{1}{2}\}{0,ψ1​,…,ψB−1​,21​}的阈值，其中$(u,v)$表示水平和垂直频率索引。默认情况下，我们使用基于八度的分区策略[60]将频率谱分解为四个不同的频率带。用于划分频率带的阈值为{0,116,18,14,12}\{0,\frac{1}{16},\frac{1}{8},\frac{1}{4},\frac{1}{2}\}{0,161​,81​,41​,21​}。

【解析】核频率分解是FBM的核心技术环节，其本质是将单一的卷积核转换为多个频率特化的子核。这个过程分为三个关键步骤：首先是尺寸对齐，将小尺寸的卷积核通过零填充扩展到与输入特征图相同的尺寸，这是进行频域操作的前提条件，因为傅里叶变换要求输入信号具有一致的空间维度。接下来是频域变换，通过离散傅里叶变换$\mathcal{F}$将空间域的卷积核转换到频域，获得其频谱表示。最后是频带分离，利用二进制掩码${\mathcal{M}}_b$在频域中选择性地保留特定频率范围内的成分，同时将其他频率成分设为零。掩码函数的设计采用了基于距离的准则，使用$\max (|u|,|v|)$来定义频率距离，这种无穷范数距离确保了频带划分的几何对称性。八度分区策略的选择基于信号处理理论，将频率谱按照2的幂次进行分割，这种分割方式与人类视觉系统的频率敏感性特征相匹配，同时保证了不同频带之间信息内容的相对平衡。分解后的每个频率带核${\mathbf{W}}_b$都专门负责处理特定频率范围的信息，为后续的空间自适应调制奠定了基础。

Convolution in the Fourier Domain. After obtaining the frequency-specific weights ${\mathbf{W}}_b$ , the output for the corresponding frequency band can be computed as follows:

$${\mathbf{Y}}_b={\mathbf{W}}_b\ast \mathbf{X},$$

where ${\mathbf{Y}}_b$ represents the output for the $b$-th frequency band.

【翻译】傅里叶域卷积。获得频率特定权重${\mathbf{W}}_b$后，相应频率带的输出可以按如下方式计算，其中${\mathbf{Y}}_b$表示第$b$个频率带的输出。

【解析】傅里叶域卷积步骤是频率分解后的自然延续，它将传统的单一卷积操作转换为多个频率特化的并行卷积。每个频率带的卷积操作${\mathbf{Y}}_b={\mathbf{W}}_b\ast \mathbf{X}$独立进行，其中频率特定权重${\mathbf{W}}_b$只包含特定频率范围内的信息，而其他频率成分已被掩码过程清零。这种设计使得每个频率带能够专注于处理其专业领域内的信息：低频带专门处理图像的整体结构和平滑变化，中频带负责捕获中等尺度的纹理和模式，而高频带则专注于细节、边缘和噪声等快速变化的成分。多个频率带的并行处理不仅保持了原始卷积的信息完整性，还为后续的空间自适应调制提供了精细化的控制粒度。每个频率带输出${\mathbf{Y}}_b$都携带着特定频率范围内的特征信息，这些信息将在下一步的空间调制过程中根据局部内容特性进行动态权重分配。

However, as discussed in [ 15 , 16 ], obtaining specific frequency bands of W directly in the spatial domain is challenging. For instance, ${\mathbf{W}}_b$ would need to be infinitely large to isolate the low-frequency part of W , since the ideal lowpass filter sinc has infinite support in spatial domain [ 15 ].

【翻译】然而，如[15, 16]中所讨论的，在空间域中直接获得W的特定频率带是具有挑战性的。例如，为了分离W的低频部分，${\mathbf{W}}_b$需要无限大，因为理想的低通滤波器sinc在空间域中具有无限支撑[15]。

【解析】这个挑战来自于信号处理的基本原理：频域和空间域之间存在不确定性原理，这类似于量子力学中的海森堡不确定性原理。在频域中具有精确截止特性的理想滤波器，在空间域中必然具有无限的空间扩展。具体来说，当我们想要创建一个完美的低通滤波器来分离特定频率带时，这个滤波器在空间域的表示是sinc函数$\frac{\sin (\pi x)}{\pi x}$，其特点是尾部衰减缓慢，理论上延伸到无穷远。这说明如果我们想在空间域直接构造频率特定的卷积核${\mathbf{W}}_b$，就需要无限大的卷积核才能实现完美的频率选择性。这在实际应用中是不可能的，因为卷积核的尺寸必须是有限的。这个根本性限制迫使研究者寻找替代方案，即转向频域处理来实现精确的频率分解。

To overcome this limitation, we perform the convolution in the Fourier domain rather than in the spatial domain. According to the Convolution Theorem [ 15 ], convolution in the spatial domain is equivalent to pointwise multiplication of the Fourier transforms in the frequency domain. Therefore, we formulate the frequency-specific convolution as:

$${\mathbf{Y}}_b={\mathcal{F}}^{-1}\left(\left({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{W})\right)\odot \mathcal{F}(\mathbf{X})\right).$$

This formulation enables the efficient computation of convolutions for each frequency band.

【翻译】为了克服这一限制，我们在傅里叶域而非空间域执行卷积。根据卷积定理[15]，空间域中的卷积等价于频域中傅里叶变换的逐点乘法。因此，我们将频率特定卷积表述为：这个表述使得每个频率带的卷积计算变得高效。

【解析】卷积定理是信号处理中的核心理论，它建立了空间域卷积与频域乘法之间的等价关系。在空间域中，卷积是一个计算复杂度为$O(N^2)$的操作，而在频域中，这个操作变成了简单的逐元素乘法，复杂度仅为$O(N)$。公式${\mathbf{Y}}_b={\mathcal{F}}^{-1}\left(\left({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{W})\right)\odot \mathcal{F}(\mathbf{X})\right)$的计算流程如下：首先，通过$\mathcal{F}(\mathbf{W})$和$\mathcal{F}(\mathbf{X})$将卷积核和输入特征图分别变换到频域；然后，使用二进制掩码${\mathcal{M}}_b$对卷积核的频谱进行选择性过滤，只保留第$b$个频率带的信息；接着，进行频域乘法$\left({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{W})\right)\odot \mathcal{F}(\mathbf{X})$，这等价于空间域的卷积操作；最后，通过逆傅里叶变换${\mathcal{F}}^{-1}$将结果转回空间域。这种方法不仅解决了空间域滤波器无限支撑的问题，还提供了精确的频率选择能力，使得每个频率带的处理都能达到理论上的完美分离效果。

Spatially Variant Modulation. After obtaining the output results for each frequency band, a modulation map ${\mathbf{A}}_b\in {\mathbb{R}}^{h\times w}$ is generated to control the uence of each frequency band at each spatial location. ${\mathbf{A}}_b$ can be easily implemented using a standard convolution layer followed by a sigmoid function. Consequently, the output feature map $\mathbf{Y}$ is computed as:

$$\mathbf{Y}=\sum _{b=0}^{B-1}({\mathbf{A}}_b\odot {\mathbf{Y}}_b).$$

This approach allows FBM to adjust frequency responses dynamically at each spatial location, enhancing the model’s ability to capture context-specific features across the image effectively.

【翻译】空间变化调制。在获得每个频率带的输出结果后，生成调制图${\mathbf{A}}_b\in {\mathbb{R}}^{h\times w}$来控制每个频率带在每个空间位置的影响。${\mathbf{A}}_b$可以通过标准卷积层后跟sigmoid函数来轻松实现。因此，输出特征图$\mathbf{Y}$的计算如下：这种方法允许FBM在每个空间位置动态调整频率响应，有效增强模型捕获图像中上下文特定特征的能力。

【解析】传统卷积在整个特征图上应用相同的滤波器，而空间变化调制引入了位置感知的自适应机制。调制图${\mathbf{A}}_b$的生成过程涉及学习每个空间位置对不同频率成分的需求：在包含精细纹理的区域，高频调制系数会自动增大；在平滑区域，低频调制系数占主导；在边缘区域，中频成分会被强化。sigmoid激活函数确保调制系数在$[0,1]$范围内，提供了从完全抑制到完全保留的连续控制能力。最终的输出$\mathbf{Y}={\sum }_{b=0}^{B-1}({\mathbf{A}}_b\odot {\mathbf{Y}}_b)$是所有频率带经过空间调制后的加权组合，这种设计使得模型能够根据局部内容特性动态重新分配不同频率成分的重要性。每个像素位置都有自己独特的频率响应配置文件，这种细粒度的控制能力使模型能够同时处理图像中的多尺度信息，并根据上下文自适应地强调最相关的频率成分。

Practical Implementation. Mathematically, the obtation of ${\mathbf{Y}}_b$ in Equation ( 7 ) is equivalent to:

$${\mathbf{Y}}_b={\mathcal{F}}^{-1}\left(\mathcal{F}(\mathbf{W})\odot \left({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{X})\right)\right)=\mathbf{W}\ast {\mathbf{X}}_b.$$

【翻译】实际实现。在数学上，公式(7)中${\mathbf{Y}}_b$的获得等价于：

【解析】原始公式通过对卷积核进行频率分解，而等价公式则是对输入特征图进行频率分解。这种等价性源于傅里叶变换的线性性质和卷积定理的对称性。具体来说，$\mathcal{F}(\mathbf{W})\odot \left({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{X})\right)$可以重新组织为$\left({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{X})\right)\odot \mathcal{F}(\mathbf{W})$，因为逐元素乘法具有交换律。进一步地，${\mathbf{X}}_b={\mathcal{F}}^{-1}({\mathcal{M}}_b\odot \mathcal{F}(\mathbf{X}))$表示输入特征图的第$b$个频率带分量，最终的$\mathbf{W}\ast {\mathbf{X}}_b$表示完整卷积核与频率分解后的输入进行卷积。等价性为实际实现提供了灵活性：可以选择分解卷积核或分解输入特征图，两种方法在数学上完全等价，但在计算效率和内存使用方面可能有所不同。

The above derivation reveals that decomposing the convolution kernel into frequency bands ( i.e ., ${\mathbf{W}}_b={\mathcal{M}}_b\odot \mathbf{W})$ is mathematically equivalent to decomposing the input feature map into corresponding frequency components ( i.e ., ${\mathbf{X}}_b={\mathcal{M}}_b\odot \mathbf{X})$ ). This equivalence stems from the commutative property of convolution and the linearity of the Fourier transform. Specifically, modulating and convolving frequency-specific weights with the original feature map can be reinterpreted as first filtering the feature map into sub-bands and then convolving with the full kernel:

$$\mathbf{Y}=\sum _{b=0}^{B-1}\left({\mathbf{A}}_b\odot {\mathbf{X}}_b\right)\ast \mathbf{W}.$$

【翻译】上述推导揭示了将卷积核分解为频率带（即${\mathbf{W}}_b={\mathcal{M}}_b\odot \mathbf{W}$）在数学上等价于将输入特征图分解为相应的频率分量（即${\mathbf{X}}_b={\mathcal{M}}_b\odot \mathbf{X}$）。这种等价性源于卷积的交换性质和傅里叶变换的线性性。具体来说，使用频率特定权重对原始特征图进行调制和卷积，可以重新解释为首先将特征图过滤成子带，然后与完整卷积核进行卷积：

【解析】传统上，我们可能认为分解卷积核和分解输入特征图是两种不同的操作，但数学证明了它们本质上是相同的。这种等价性的根本原因在于卷积运算的交换律：$\mathbf{A}\ast \mathbf{B}=\mathbf{B}\ast \mathbf{A}$，以及傅里叶变换的线性性质：$\mathcal{F}(\alpha \mathbf{X}+\beta \mathbf{Y})=\alpha \mathcal{F}(\mathbf{X})+\beta \mathcal{F}(\mathbf{Y})$。在频域中，掩码${\mathcal{M}}_b$可以作用于卷积核的频谱或输入特征图的频谱，由于逐元素乘法的交换性，这两种方式在数学上完全等价。新公式$\mathbf{Y}={\sum }_{b=0}^{B-1}\left({\mathbf{A}}_b\odot {\mathbf{X}}_b\right)\ast \mathbf{W}$展示了另一种实现路径：首先将输入特征图分解为不同频率子带${\mathbf{X}}_b$，然后应用空间调制权重${\mathbf{A}}_b$，最后与完整的卷积核$\mathbf{W}$进行卷积。

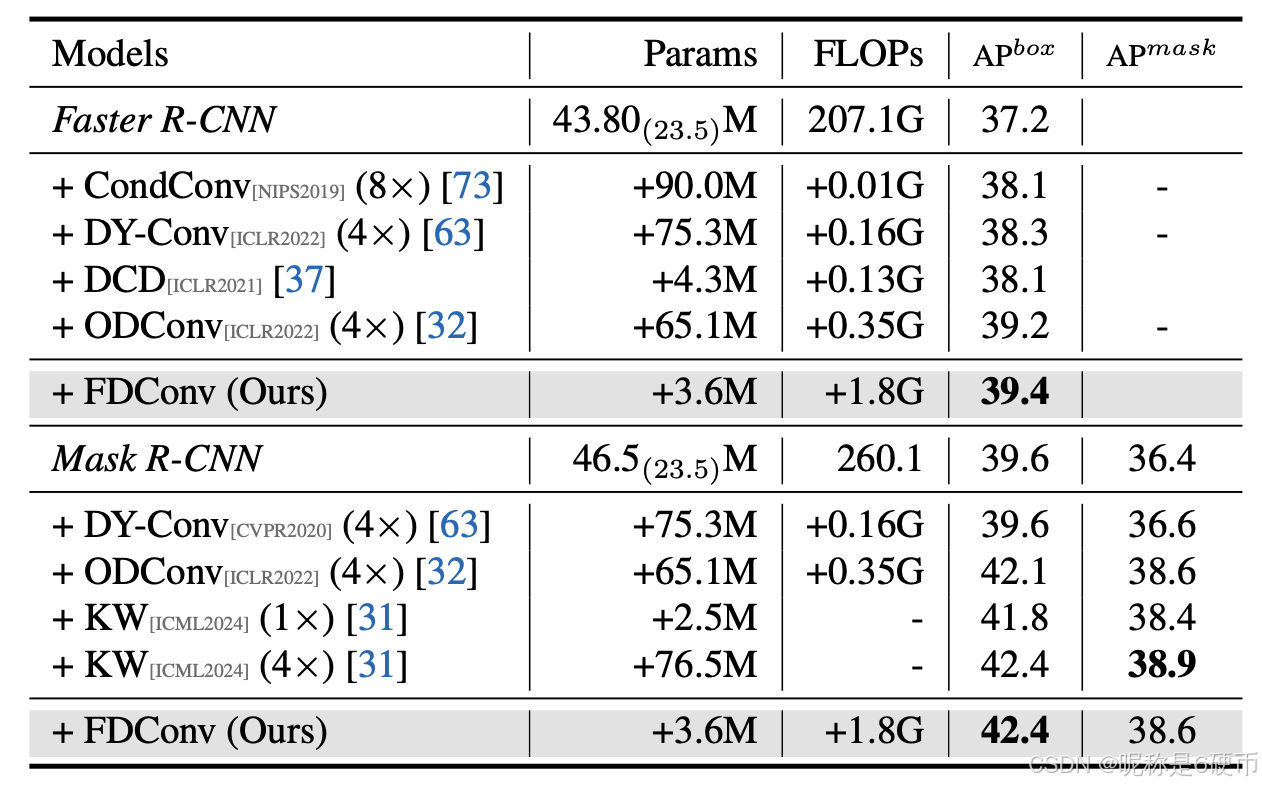
Table 1. Results comparison on the COCO validation set [ 42 ]. The numbers in brackets indicate the parameters of the backbone. Additionally, the notation $n\times$ denotes the convolutional parameter budget of each dynamic convolution relative to the standard convolution in the backbone.

【翻译】表1. COCO验证集[42]上的结果比较。括号中的数字表示骨干网络的参数量。此外，符号$n\times$表示每个动态卷积相对于骨干网络中标准卷积的卷积参数预算。

This perspective bridges two seemingly distinct paradigms: frequency-adaptive weight decomposition and multi-band feature processing. The equivalent implementation not only circumvents the impracticality of infinite spatial support in ideal frequency filters but also provides implementation flexibility, one can choose to implement frequency decomposition on either weights or features based on computational constraints, while maintaining strict mathematical equivalence through Fourier duality.

【翻译】这种观点连接了两个看似不同的范式：频率自适应权重分解和多带特征处理。等价实现不仅规避了理想频率滤波器无限空间支撑的不切实际性，还提供了实现灵活性，可以根据计算约束选择在权重或特征上实现频率分解，同时通过傅里叶对偶性保持严格的数学等价性。

【解析】这段话总结了FDConv方法的技术优势。从理论角度看，它统一了两个原本独立的信号处理概念：一是对卷积核进行频率域分解（传统的滤波器设计思路），二是对输入信号进行多带分析（信号处理中的子带编码思想）。这种统一性说明深度学习中的卷积操作与经典信号处理理论存在深层次的联系。从实践角度看，数学等价性解决了一个根本性的工程问题：理想频率滤波器在空间域的无限支撑问题。传统方法要在空间域构造频率选择性滤波器会遇到截断误差和计算复杂度问题，而通过频域操作可以实现精确的频率分离。更重要的是，这种等价性提供了实现策略的多样性：当卷积核较小而特征图较大时，分解卷积核可能更有效；当卷积核较大而特征图较小时，分解特征图可能更优。傅里叶对偶性保证了无论选择哪种实现方式，最终结果都是数学上完全一致的，这为不同硬件平台和应用场景的优化提供了理论保障。

4. Experiment

Datasets and Metrics. We evaluate our methods on challenging semantic segmentation datasets, including Cityscapes [ 10 ] and ADE20K [ 79 ], using mean Intersection over Union (mIoU) for segmentation [ 1 , 6 , 13 , 45 , 48 ] and Average Precision (AP) for object detection and instance segmentation [ 22 , 59 ].

【翻译】数据集和指标。我们在具有挑战性的语义分割数据集上评估我们的方法，包括Cityscapes [ 10 ]和ADE20K [ 79 ]，对分割任务使用平均交并比(mIoU)[ 1 , 6 , 13 , 45 , 48 ]，对目标检测和实例分割任务使用平均精度(AP)[ 22 , 59 ]。

Implementation Details. We follow the settings from the original papers for UPerNet [ 70 ], Mask2Former [ 8 ], MaskDINO [ 72 ], Swin Transformer [ 46 ], and ConvNeXt [ 31 , 47 ]. On COCO [ 41 ], we adhere to standard practices [ 21 , 57 , 68 ], training detection and segmentation models for 12 epochs ( $1\times$ schedule). We empirically set the number of weights to 64 for FDConv. More details are described in the supplementary.

【翻译】实现细节。我们对UPerNet [ 70 ]、Mask2Former [ 8 ]、MaskDINO [ 72 ]、Swin Transformer [ 46 ]和ConvNeXt [ 31 , 47 ]遵循原始论文的设置。在COCO [ 41 ]上，我们遵循标准做法[ 21 , 57 , 68 ]，训练检测和分割模型12个epoch ($1\times$调度)。我们凭经验将FDConv的权重数量设置为64。更多细节在补充材料中描述。

5. Main Results

In this section, we evaluate our FDConv on a range of tasks, including object detection, instance segmentation, and semantic segmentation, using standard benchmarks such as COCO [ 42 ], ADE20K [ 79 ], and Cityscapes [ 10 ].

【翻译】在本节中，我们在一系列任务上评估我们的FDConv，包括目标检测、实例分割和语义分割，使用标准基准数据集如COCO [ 42 ]、ADE20K [ 79 ]和Cityscapes [ 10 ]。

We compare our FDConv with state-of-the-art dynamic convolutional methods, including CondConv [ 73 ], DYConv [ 63 ], DCD [ 37 ], ODConv [ 32 ] and KW [ 31 ]. The experiments demonstrate that FDConv not only achieves the highest performance across detection and segmentation tasks but also does so with large reduced parameter overhead. Moreover, FDConv is highly versatile, it can easily combine with state-of-the-art ConvNet models like ConvNeXt [ 47 ] and apply to transformer architectures such as Swin-T [ 46 ], Mask2Former [ 8 ], and MaskDINO [ 34 ]. The experimental results demonstrate that FDConv achieves notable improvements over both conventional competitors and state-of-the-art baselines.

【翻译】我们将FDConv与最先进的动态卷积方法进行比较，包括CondConv [ 73 ]、DYConv [ 63 ]、DCD [ 37 ]、ODConv [ 32 ]和KW [ 31 ]。实验表明，FDConv不仅在检测和分割任务中达到最高性能，而且在大幅减少参数开销的情况下实现了这一点。此外，FDConv具有高度的通用性，它可以轻松与最先进的ConvNet模型（如ConvNeXt [ 47 ]）结合，并应用于transformer架构，如Swin-T [ 46 ]、Mask2Former [ 8 ]和MaskDINO [ 34 ]。实验结果表明，FDConv在传统竞争对手和最先进基线上都取得了显著改进。

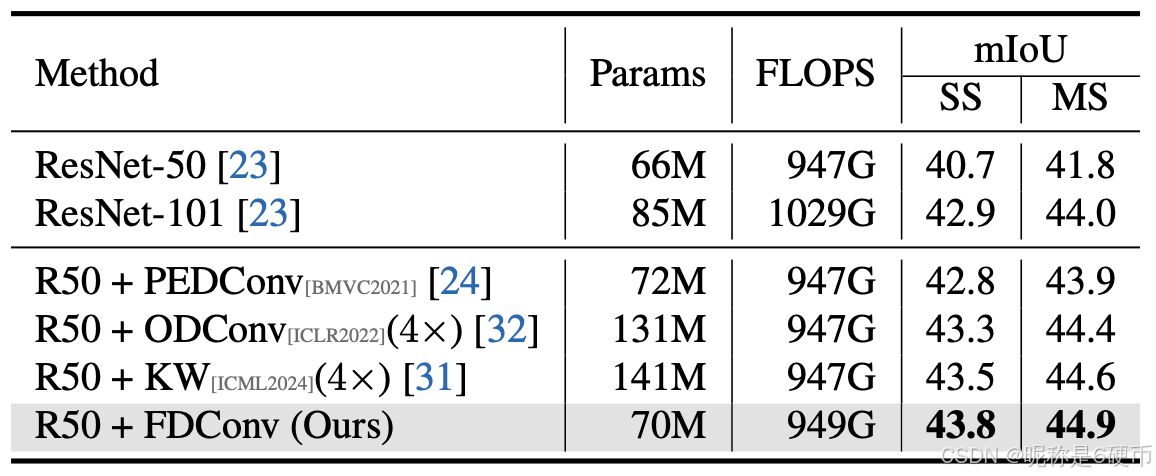
Table 2. Quantitative comparisons on semantic segmentation tasks with UPerNet [ 70 ] on the ADE20K validation set.

【翻译】表2. 在ADE20K验证集上使用UPerNet [ 70 ]进行语义分割任务的定量比较。

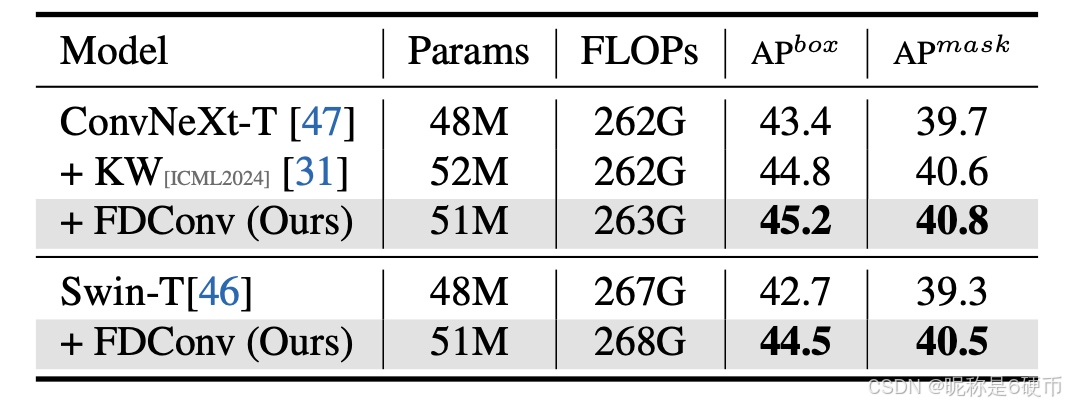
Table 3. Object detection and instance segmentation performance on the COCO dataset [ 42 ] with the Mask R-CNN detector [ 22 ]. All models are trained with a $1\times$ schedule [ 21 , 68 ].

【翻译】表3. 在COCO数据集[ 42 ]上使用Mask R-CNN检测器[ 22 ]的目标检测和实例分割性能。所有模型都使用$1\times$调度进行训练[ 21 , 68 ]。

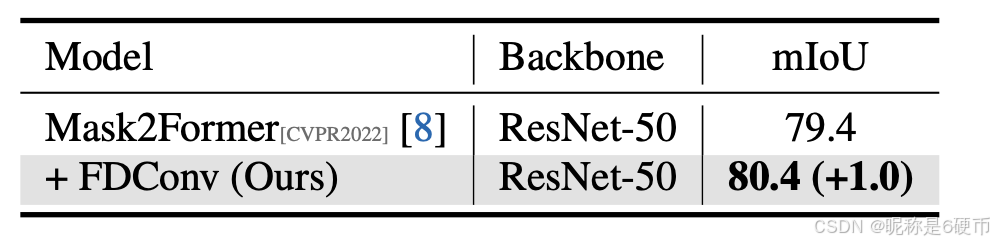
Table 4. Semantic segmentation results on Cityscapes [ 10 ] using the recent state-of-the-art Mask2Former [ 8 ].

【翻译】表4. 使用最新最先进的Mask2Former [ 8 ]在Cityscapes [ 10 ]上的语义分割结果。

Table 5. Semantic segmentation results with recent state-of-the-art large models Mask2Former [ 8 ] and MaskDINO [ 34 ] on ADE20K. Backbones pre-trained on ImageNet-22K are marked with † .

【翻译】表5. 在ADE20K上使用最新最先进的大型模型Mask2Former [ 8 ]和MaskDINO [ 34 ]的语义分割结果。在ImageNet-22K上预训练的骨干网络用 † 标记。

Object Detection. Table 1 shows the results obtained by Faster R-CNN with various dynamic convolutional modules. Our FDConv module, despite adding only $+3.6\mathbf{M}$ parameters and $+1.8\mathrm{G}$ FLOPs, achieves an $\mathbf{A}{\mathbf{P}}^{box}$ of 39.4, $2.2\%$ improvement over the baseline and outperforms CondConv [ 73 ], DY-Conv [ 63 ], and DCD [ 37 ], and ODConv [ 32 ], which require substantially higher parameter budgets. FDConv not only surpasses other methods in terms of accuracy but also achieves this with a minimal computational footprint, positioning it as a highly efficient enhancement for object detection tasks.

【翻译】目标检测。表1显示了Faster R-CNN使用各种动态卷积模块获得的结果。我们的FDConv模块，尽管仅增加了$+3.6\mathbf{M}$参数和$+1.8\mathrm{G}$ FLOPs，但实现了39.4的$\mathbf{A}{\mathbf{P}}^{box}$，比基线提高$2.2\%$，并且优于CondConv [ 73 ]、DY-Conv [ 63 ]、DCD [ 37 ]和ODConv [ 32 ]，而这些方法需要大幅更高的参数预算。FDConv不仅在准确性方面超越了其他方法，而且以最小的计算占用实现了这一点，将其定位为目标检测任务的高效增强方法。

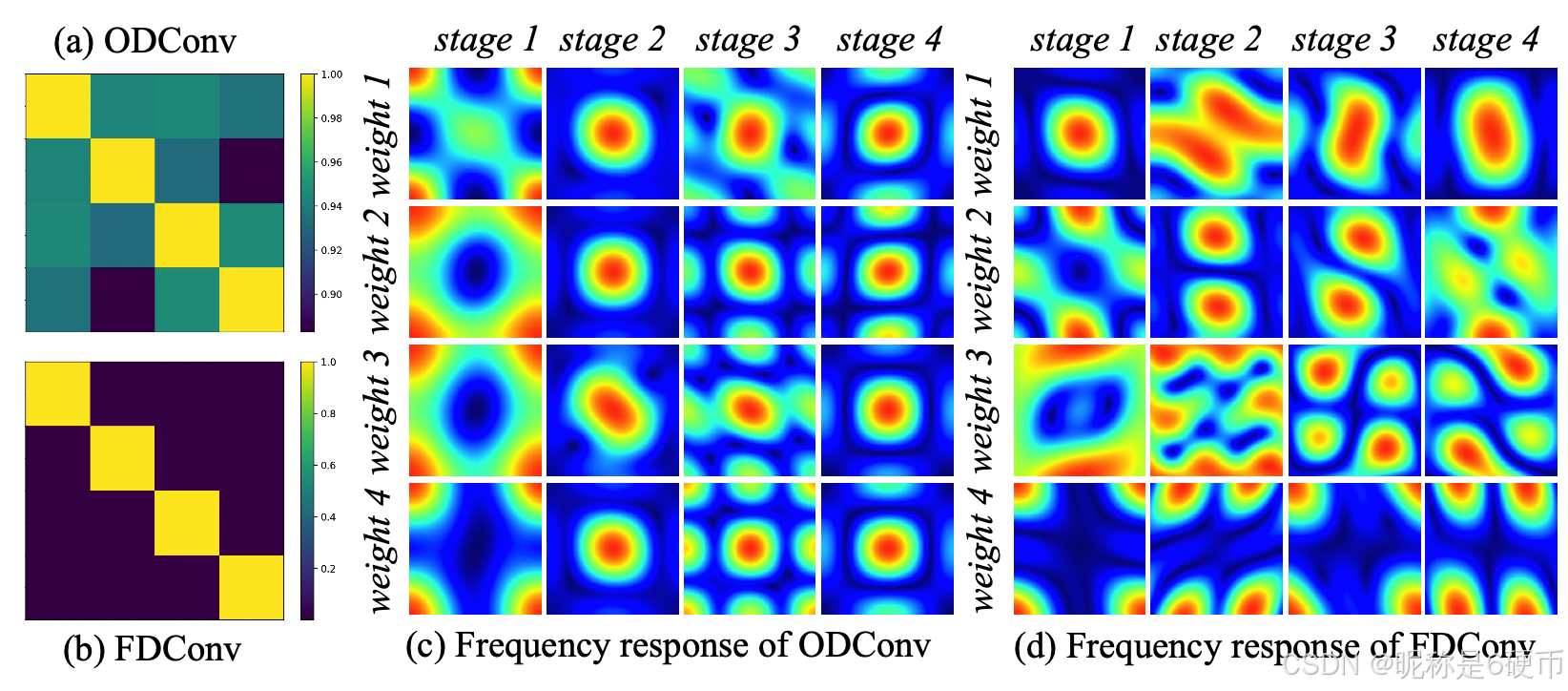
Figure 5. Weight similarity and frequency analyses. (a) demonstrates that existing dynamic convolution methods, such as ODConv [ 32 ], exhibit high cosine similarity $(>0.88)$ among their 4 learned weights. The frequency analysis in © shows 4 representative ODConv layers from stage 1 to stage 4 of the model, and it demonstrates large homogeneity between the 4 weights. In contrast, the 4 weights of our proposed FDConv show zero similarity in (b), allowing each kernel to learn distinct and complementary features with diversified frequency response, as shown in (d).

【翻译】图5. 权重相似性和频率分析。(a)表明现有的动态卷积方法，如ODConv [ 32 ]，在其4个学习权重之间表现出高余弦相似性$(>0.88)$。©中的频率分析显示了模型第1到第4阶段的4个代表性ODConv层，它表明4个权重之间存在很大的同质性。相比之下，我们提出的FDConv的4个权重在(b)中显示出零相似性，允许每个核学习具有多样化频率响应的独特和互补特征，如(d)所示。

Instance Segmentation. We further evaluate FDConv using Mask R-CNN [ 22 ] as the base model, following [ 31 , 32 ]. FDConv achieves an $\mathbf{A}{\mathbf{P}}^{box}$ of 42.4 and ${\mathrm{AP}}^{mask}$ of 38.6, surpassing or matching recent high-performing methods such as ODConv [ 32 ] and KW [ 31 ]. Notably, while KW [ 31 ] achieves marginally higher segmentation performance, it incurs a $4\times$ increa parameter cost $(+76.5\mathrm{M})$ , whereas FDConv adds only 3.6M.

【翻译】实例分割。我们使用Mask R-CNN [ 22 ]作为基础模型进一步评估FDConv，遵循[ 31 , 32 ]。FDConv实现了42.4的$\mathbf{A}{\mathbf{P}}^{box}$和38.6的${\mathrm{AP}}^{mask}$，超越或匹配了最近的高性能方法，如ODConv [ 32 ]和KW [ 31 ]。值得注意的是，虽然KW [ 31 ]实现了略高的分割性能，但它产生了$4\times$的参数成本增加$(+76.5\mathrm{M})$，而FDConv仅增加3.6M。

Semantic Segmentation. As shown in Table 2 , FDConv achieves the highest mIoU scores, with a single-scale (SS) mIoU of 43.8. Notably, FDConv accomplishes this performance with fewer additional parameters (70M total) compared to ODConv [ 32 ] (131M) and KW [ 31 ] (141M), underscoring its parameter efficiency while achieving superior segmentation quality.

【翻译】语义分割。如表2所示，FDConv实现了最高的mIoU分数，单尺度(SS) mIoU为43.8。值得注意的是，FDConv以更少的额外参数(总共70M)实现了这一性能，相比ODConv [ 32 ] (131M)和KW [ 31 ] (141M)，强调了其参数效率，同时实现了优越的分割质量。

Combination with Advanced Architectures. Additionally, we test FDConv on object detection and instance segmentation tasks using the COCO [ 42 ] to examine its crossarchitecture applicability. Table 3 demonstrates that FDConv outperforms other methods, including KW [ 31 ], when applied to both ConvNeXt [ 47 ] and Swin Transformer [ 46 ] backbones. It achieved an $\mathrm{A}{\mathrm{P}}^{\mathrm{box}}$ of 45.2 with ConvNeXtT [ 47 ] and 44.5 with Swin-T [ 46 ], along with enhanced $\mathrm{A}{\mathrm{P}}^{\mathrm{mask}}$ scores. These results underscore FDConv’s consistent generalization capabilities across various architectures.

【翻译】与先进架构的结合。此外，我们使用COCO [ 42 ]在目标检测和实例分割任务上测试FDConv，以检查其跨架构的适用性。表3表明，当应用于ConvNeXt [ 47 ]和Swin Transformer [ 46 ]骨干网络时，FDConv优于其他方法，包括KW [ 31 ]。它在ConvNeXtT [ 47 ]上实现了45.2的$\mathrm{A}{\mathrm{P}}^{\mathrm{box}}$，在Swin-T [ 46 ]上实现了44.5，同时提高了$\mathrm{A}{\mathrm{P}}^{\mathrm{mask}}$分数。这些结果强调了FDConv在各种架构中的一致泛化能力。

Combination with Heavy Models. To assess the adaptability of our FDConv with advanced architectures, we incorporate FDConv into the state-of-the-art Mask2Former [ 8 ] and MaskDINO [ 34 ] frameworks. Table 4 shows that Mask2Former-ResNet-50 with FDConv achieves an mIoU improvement of $+1.0$ (from 79.4 to 80.4) on Cityscapes [ 10 ]. On ADE20K [ 79 ], Table 5 highlights that with FDConv, Mask2Former-Swin-B [ 8 ] achieves an mIoU improvement of $+1.0$ (from 53.9 to 54.9), while MaskDINO-Swin-L [ 34 ] achieves an mIoU improvement of $+0.5$ (from 56.6 to 57.2). These consistent gains demonstrate that FDConv can effectively enhance heavy architectures.

【翻译】与重型模型的结合。为了评估我们的FDConv与先进架构的适应性，我们将FDConv整合到最先进的Mask2Former [ 8 ]和MaskDINO [ 34 ]框架中。表4显示，带有FDConv的Mask2Former-ResNet-50在Cityscapes [ 10 ]上实现了$+1.0$的mIoU改进(从79.4到80.4)。在ADE20K [ 79 ]上，表5强调，使用FDConv，Mask2Former-Swin-B [ 8 ]实现了$+1.0$的mIoU改进(从53.9到54.9)，而MaskDINO-Swin-L [ 34 ]实现了$+0.5$的mIoU改进(从56.6到57.2)。这些一致的提升表明FDConv可以有效增强重型架构。

Figure 6. Visualization of Frequency Band Modulation. (a) shows the input images and their corresponding ground truth (GT). (b)–(d) display the modulation maps for different frequency bands, ranging from low to high. (e) and (f) visualize the feature frequency spectrum.

【翻译】图6. 频率带调制的可视化。(a)显示输入图像及其对应的真实标注(GT)。(b)-(d)显示不同频率带的调制图，从低到高。(e)和(f)可视化特征频率谱。

6. Analyses and Discussion

We use ResNet-50 [ 76 ] as the backbone model and conduct a comprehensive analysis of the proposed FDConv. Due to space limitations, more detailed analyses and the results of ablation studies are provided in the supplementary material . Weight Similarity Analysis. We analyze the diversity of learned features in FDConv by comparing weight similarity with existing dynamic convolution methods. As shown in Figure 5(a) , traditional methods like ODConv [ 32 ] exhibit high cosine similarity $(>0.88)$ among their learned weights, indicating significant redundancy. This redundancy limits the representational capacity of the model, as each kernel learns overlapping features.

【翻译】我们使用ResNet-50 [ 76 ]作为骨干模型，并对所提出的FDConv进行了全面分析。由于篇幅限制，更详细的分析和消融研究结果在补充材料中提供。权重相似性分析。我们通过与现有动态卷积方法比较权重相似性来分析FDConv中学习特征的多样性。如图5(a)所示，ODConv [ 32 ]等传统方法在其学习权重之间表现出高余弦相似性$(>0.88)$，表明存在显著冗余。这种冗余限制了模型的表示能力，因为每个核学习重叠的特征。

In contrast, FDConv kernels exhibit zero cosine similarity (Figure 5(b) ), suggesting that each kernel captures unique, complementary features. This diversity enhances the model’s expressiveness and adaptability.

【翻译】相比之下，FDConv核表现出零余弦相似性(图5(b))，表明每个核捕获独特的、互补的特征。这种多样性增强了模型的表达能力和适应性。

Weight Frequency Analysis. As shown in Figure 5© , frequency analysis reveals that ODConv weights exhibit limited frequency diversity across different stages. In contrast, FDConv demonstrates a more diversified frequency response (Figure 5(d) ), capturing a broader range of frequency characteristics. This allows FDConv to model a richer set of features, further improving its ability to represent complex input data.

【翻译】权重频率分析。如图5©所示，频率分析显示ODConv权重在不同阶段表现出有限的频率多样性。相比之下，FDConv展示了更多样化的频率响应(图5(d))，捕获更广泛的频率特征。这允许FDConv建模更丰富的特征集，进一步提高其表示复杂输入数据的能力。

Feature Visualization for FBM. As shown in Figure 6 , we visualize the modulation maps for each frequency band. For better performance, we empirically set the modulation map for the lowest frequency band to all 1. We observe that higher modulation values are concentrated around object boundaries, with this effect becoming more pronounced in higher frequency bands (Figure 6(b)-(d) ). In contrast, lower frequency bands exhibit regions of high modulation within the objects themselves (Figure 6© ).

【翻译】FBM的特征可视化。如图6所示，我们可视化了每个频率带的调制图。为了更好的性能，我们经验性地将最低频率带的调制图设置为全1。我们观察到较高的调制值集中在目标边界周围，这种效应在较高频率带中变得更加明显(图6(b)-(d))。相比之下，较低频率带在目标内部表现出高调制区域(图6©)。

This selective modulation enables FDConv to suppress high frequencies in regions such as the background and object centers, which do not contribute significantly to accurate predictions. As seen in Figure 6(e)-(f) , high-frequency noise in the feature map is largely reduced, and the spectrum in Figure 6(g)-(h) further confirms the suppression of unnecessary high-frequency components. Meanwhile, as shown in Figure 6(e)-(f) , foreground features are enhanced, leading to more accurate and complete representations that benefit dense prediction tasks.

【翻译】这种选择性调制使FDConv能够在背景和目标中心等对准确预测贡献不大的区域抑制高频。如图6(e)-(f)所示，特征图中的高频噪声大大减少，图6(g)-(h)中的频谱进一步确认了不必要高频分量的抑制。同时，如图6(e)-(f)所示，前景特征得到增强，导致更准确和完整的表示，有利于密集预测任务。

7. Conclusion

We introduced Frequency Dynamic Convolution (FDConv), which enhances the frequency adaptability of parallel weights without increasing parameter overhead. By incorporating Fourier Disjoint Weight (FDW), Kernel Spatial Modulation (KSM), and Frequency Band Modulation (FBM), FDConv addresses the limitations of existing dynamic convolution methods, including restricted frequency diversity in parallel weights and high parameter costs.

【翻译】我们介绍了频率动态卷积(FDConv)，它在不增加参数开销的情况下增强了并行权重的频率适应性。通过结合傅里叶分离权重(FDW)、核空间调制(KSM)和频率带调制(FBM)，FDConv解决了现有动态卷积方法的局限性，包括并行权重中有限的频率多样性和高参数成本。

Our analysis shows that FDConv achieves greater frequency diversity, enabling better feature capture across spatial and frequency domains. Extensive experiments on object detection, segmentation, and classification demonstrate that FDConv outperforms prior state-of-the-art methods, with only a modest increase in parameter cost compared to others that incur much higher overhead. FDConv can be easily integrated into existing architectures, including both ConvNets and vision transformers, making it a versatile and efficient solution for a wide range of computer vision tasks. We hope our analyses and finding would new direction for building more efficient and powerful vision models.

【翻译】我们的分析显示FDConv实现了更大的频率多样性，能够在空间和频率域中更好地捕获特征。在目标检测、分割和分类上的大量实验表明，FDConv优于之前的最先进方法，相比其他产生更高开销的方法，仅增加适度的参数成本。FDConv可以轻松集成到现有架构中，包括ConvNets和视觉变换器，使其成为广泛计算机视觉任务的通用且高效的解决方案。我们希望我们的分析和发现能为构建更高效和强大的视觉模型提供新方向。