2106. 摘水果，梳理思路

题目概要

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

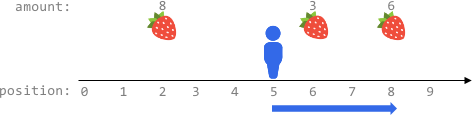
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：

• 向右移动到位置 6 ，摘到 3 个水果
• 向右移动到位置 8 ，摘到 6 个水果
  移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

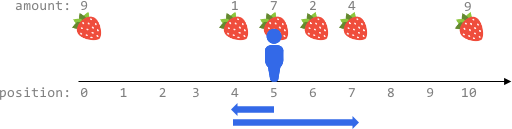
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：

• 在初始位置 5 ，摘到 7 个水果
• 向左移动到位置 4 ，摘到 1 个水果
• 向右移动到位置 6 ，摘到 2 个水果
• 向右移动到位置 7 ，摘到 4 个水果
  移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

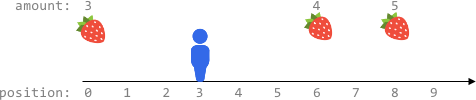
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：
$$\begin{gathered} 1<=fruits.length<=10^5 \\ fruits[i].length==2 \\ 0<=startPos,positioni<=2\ast 10^5 \\ 对于任意i>0，positioni-1<positioni均成立（下标从0开始计数） \\ 1<=amounti<=10^4 \\ 0<=k<=2\ast 10^5 \end{gathered}$$

java 解法

public int maxTotalFruits(int[][] fruits, int startPos, int k) {int n = fruits.length;// 提取位置和数量，方便操作int[] positions = new int[n];int[] amounts = new int[n];for (int i = 0; i < n; i++) {positions[i] = fruits[i][0];  // 位置amounts[i] = fruits[i][1];    // 水果数量}// 前缀和数组：prefix[i] 表示前 i 个位置的水果总数int[] prefix = new int[n + 1];for (int i = 0; i < n; i++) {prefix[i + 1] = prefix[i] + amounts[i];}int maxFruits = 0;  // 记录能摘到的最大水果数int left = 0;       // 滑动窗口的左指针// 滑动窗口：右指针 right 从 0 到 n-1for (int right = 0; right < n; right++) {// 当前尝试的区间是 [left, right]int L = positions[left];      // 区间最左位置int R = positions[right];     // 区间最右位置// 计算从 startPos 出发，走完 [L, R] 所需的最少步数int steps = calculateSteps(startPos, L, R);// 如果步数超过了 k，说明走太远了，需要缩小窗口（移动 left）while (left <= right && steps > k) {left++;  // 缩小左边界if (left > right) break;L = positions[left];R = positions[right];steps = calculateSteps(startPos, L, R);}// 如果当前窗口有效，更新最大水果数if (left <= right) {int total = prefix[right + 1] - prefix[left];  // [left, right] 的水果总数maxFruits = Math.max(maxFruits, total);}}return maxFruits;
}// 计算从 startPos 出发，走完区间 [L, R] 所需的最少步数
private int calculateSteps(int startPos, int L, int R) {if (R <= startPos) {// 所有水果都在起点或左边：只向左走return startPos - L;} else if (L >= startPos) {// 所有水果都在起点或右边：只向右走return R - startPos;} else {// 水果分布在起点两侧// 方案1：先向左走到 L，再向右走到 Rint goLeftFirst = (startPos - L) * 2 + (R - startPos);// 方案2：先向右走到 R，再向左走到 Lint goRightFirst = (R - startPos) * 2 + (startPos - L);// 返回两种方案中步数更少的那个return Math.min(goLeftFirst, goRightFirst);}
}public static void main(String[] args) {Solution1 solution = new Solution1();// 示例 1int[][] fruits1 = {{2,8},{6,3},{8,6}};System.out.println(solution.maxTotalFruits(fruits1, 5, 4)); // 输出: 9// 示例 2int[][] fruits2 = {{0,9},{4,1},{5,7},{6,2},{7,4},{10,9}};System.out.println(solution.maxTotalFruits(fruits2, 5, 4)); // 输出: 14// 示例 3int[][] fruits3 = {{0,3},{6,4},{8,5}};System.out.println(solution.maxTotalFruits(fruits3, 3, 2)); // 输出: 0
}

详解

目的：将二维信息解耦为两个一维数组，便于后续使用双指针、二分查找等操作。

int n = fruits.length;// 提取位置和数量，方便操作
int[] positions = new int[n];
int[] amounts = new int[n];
for (int i = 0; i < n; i++) {positions[i] = fruits[i][0];  // 位置amounts[i] = fruits[i][1];    // 水果数量
}

前缀和（Prefix Sum）用来快速计算总和的一种方式
第 i+1 个累计值 = 第 i 个累计值 + 第 i 个位置的水果数

// 前缀和数组：prefix[i] 表示前 i 个位置的水果总数
int[] prefix = new int[n + 1];
for (int i = 0; i < n; i++) {prefix[i + 1] = prefix[i] + amounts[i];
}

拿示例 1： 举例
fruits = [[2,8], [6,3], [8,6]]
最终前缀和数组

prefix[i]	含义	对应的水果
prefix[0] = 0	前 0 个位置的水果总数	什么都没有
prefix[1] = 8	前 1 个位置的水果总数	位置 2：8 个
prefix[2] = 11	前 2 个位置的水果总数	位置 2+6：8+3=11
prefix[3] = 17	前 3 个位置的水果总数	位置 2+6+8：8+3+6=17

用前缀和快速算“某段区间的水果总数
🌰 例子 1：只摘位置 6 的水果（第 1 个位置）

• left = 1, right = 1
• 总数 = prefix[right+1] - prefix[left] = prefix[2] - prefix[1] = 11 - 8 = 3 ✅

🌰 例子 2：摘位置 6 和 8 的水果（第 1 和第 2 个位置）

• left = 1, right = 2
• 总数 = prefix[3] - prefix[1] = 17 - 8 = 9 ✅
  也就是 3 + 6 = 9

🌰 例子 3：摘所有水果（第 0 到第 2 个位置）

• left = 0, right = 2
• 总数 = prefix[3] - prefix[0] = 17 - 0 = 17 ✅

🌰 例子 4：只摘位置 2 的水果（第 0 个位置）

• left = 0, right = 0
• 总数 = prefix[1] - prefix[0] = 8 - 0 = 8
  这在滑动窗口中特别有用，因为 right 每移动一次，都要算一次区间和。

从左向右，滑动窗口
我们要在最多走 k 步的前提下，从起点 startPos 出发，摘到最多的水果。
maxFruits：就像一个“最高分记录”，通过 在 合理的 k 步条件下获取的最多水果数
外层循环：右指针 right 不断向右扩展
right 从 0 开始，一步步向右移动（0 → 1 → 2 → …）
每次 right 向右一格，就相当于我们想多摘一个位置的水果

for (int right = 0; right < n; right++) {

当前尝试的区间 [left, right]
拿示例 1： 举例
fruits = [[2,8], [6,3], [8,6]]
positions = [2, 6, 8]
那么 以下就会从

right	left	区间	步数	是否可达	水果数	maxFruits
0	0	[2]	3	✅	8	8
1	0	[2,6]	5	❌ → left=1	-	-
	1	[6]	1	✅	3	max(8,3)=8
2	1	[6,8]	3	✅	9	max(8,9)=9

int L = positions[left];      // 区间最左位置
int R = positions[right];     // 区间最右位置

计算区间区间步数
计算走完这个区间需要多少步
left <= right 缩小空间，保持空间合法性
steps > k 步数超过k步后，进入 while 调整左侧空间，使步数减少，
while (left <= right && steps > k) 用while 发现 septs 直到 空间合法后跳出循环

// 计算从 startPos 出发，走完 [L, R] 所需的最少步数
int steps = calculateSteps(startPos, L, R);// 如果步数超过了 k，说明走太远了，需要缩小窗口（移动 left）
while (left <= right && steps > k) {left++;  // 缩小左边界if (left > right) break;L = positions[left];R = positions[right];steps = calculateSteps(startPos, L, R);
}

校验合法性，并更新水果数
prefix[right + 1] - prefix[left] 这边用到了上面 所写的 前缀和 计算累计数量， left 跟 right 是 对应的坐标点，由于前缀和 第一个坐标点为 0 所以需要加1

prefix[i]	含义	对应的水果
prefix[0] = 0	前 0 个位置的水果总数	什么都没有
prefix[1] = 8	前 1 个位置的水果总数	位置 2：8 个
prefix[2] = 11	前 2 个位置的水果总数	位置 2+6：8+3=11
prefix[3] = 17	前 3 个位置的水果总数	位置 2+6+8：8+3+6=17

right + 1 前 right+1 个数的总和
left 前 left 个数的总和

amounts:     [ 8 ,  3 ,  6 ]↑    ↑    ↑
索引:         0    1    2prefix:  [0,  8,  11,  17]↑   ↑   ↑    ↑0   1   2    3

继续用示例1
fruits = [[2,8],[6,3],[8,6]]
比如 ：获取 位置为6 的 水果， 由于 前缀和的缘故 第一个是固定值，后面的值是累加过来的
prefix[right + 1] - prefix[left] = prefix[2] - prefix[1] = 11 - 8 = 3
Math.max 对比 两数大小

// 如果当前窗口有效，更新最大水果数
if (left <= right) {int total = prefix[right + 1] - prefix[left];  // [left, right] 的水果总数maxFruits = Math.max(maxFruits, total);
}

计算步数
R <= startPos 从步数左侧走完的步数， 上面 for 循环 R 是在一步步从左走到右侧的
L >= startPos 从右侧走完的步数，L 因为上面空间缩小调整一步步走到右侧
获取 在 R 大于起始步数并 L 还没移动到右侧时 获取 中间的两种状态
(startPos - L) * 2 + (R - startPos) 先向左走到 L，再向右走到 R
(R - startPos) * 2 + (startPos - L) 先先向右走到 R，再向左走到 L
Math.min 获取两者最小步数方案，可能起始位置并不居中，导致 往回走步数减少减少的情况

// 计算从 startPos 出发，走完区间 [L, R] 所需的最少步数
private int calculateSteps(int startPos, int L, int R) {if (R <= startPos) {// 所有水果都在起点或左边：只向左走return startPos - L;} else if (L >= startPos) {// 所有水果都在起点或右边：只向右走return R - startPos;} else {// 水果分布在起点两侧// 方案1：先向左走到 L，再向右走到 Rint goLeftFirst = (startPos - L) * 2 + (R - startPos);// 方案2：先向右走到 R，再向左走到 Lint goRightFirst = (R - startPos) * 2 + (startPos - L);// 返回两种方案中步数更少的那个return Math.min(goLeftFirst, goRightFirst);}
}