C++：STL中的栈和队列的适配器deque
学习完string类、容器vector和容器list，再去学习其他容器的学习成本就非常低，容器的使用方法都大差不差，而栈和队列的底层使用了适配器，去模拟实现就没有那么麻烦，适配器也是一种容器，但是这种容器兼备栈和队列需要的特性，通过观察栈和队列的码源更能体会到适配器的方便和厉害之处。虽然stack和queue中也可以存放元素，但在STL中并没有将其划分在容器的行列，而是将其称为容器适配 器，这是因为stack和队列只是对其他容器的接口进行了包装，STL中stack和queue默认使用deque。
目录
双端队列：deque
deque的优缺点
栈和队列的模拟实现
优先级队列的模拟实现
priority_queue初始化
向下调整和向上调整算法
priority_queue插入和删除
priority_queue其它接口
对比总结
双端队列：deque
如果熟悉一个容器的使用对于其他容器也能很快上手，所以小编在这里就不讲栈和队列的使用了，在还未学习c++之前，小编学习了数据结构虽然是C语言版的，也是初步了解了栈和队列。在C语言中栈和队列的实现，栈的特点是先进后出，是用数组来实现的，栈需要pop和top来删除数据和去数据但是在尾部，所以用一个数组就能很好的解决。队列的特点是先进先出，需要频繁的头删，如果使用数组来实现效率不高，数组头删的时间复杂度为O(N)，所以链表就是一个很好的选择。在c++中究竟是什么样的容器既能符合栈的特征，又能符合队列的特征，让我们一起往下瞧瞧吧！
在栈和队列中哪里可以用到deque呢？deque在模版中，在栈和队列显示实例化中默认的适配器是deque，当然也可以手动传vector或者list。
双端队列原理：deque(双端队列)：是一种双开口的"连续"空间的数据结构，双开口的含义是：可以在头尾两端进行插入和删除操作，且时间复杂度为O(1)，与vector比较，头插效率高，不需要搬移元素；与list比较，空间利用率比较高。
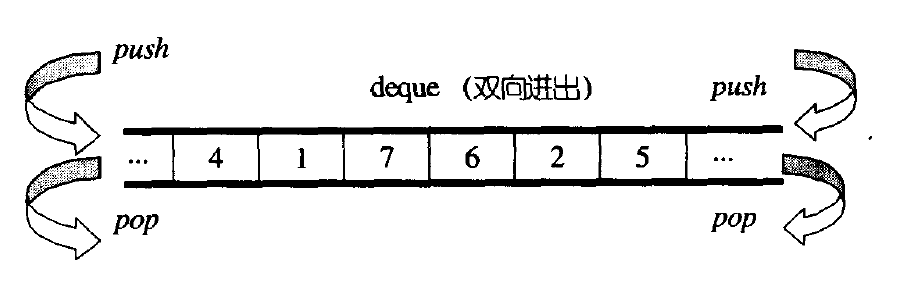
但是双端队列并不是这样连续的空间，而是像二维数组一样，一个指针数组，每个指针都对应着一块空间。
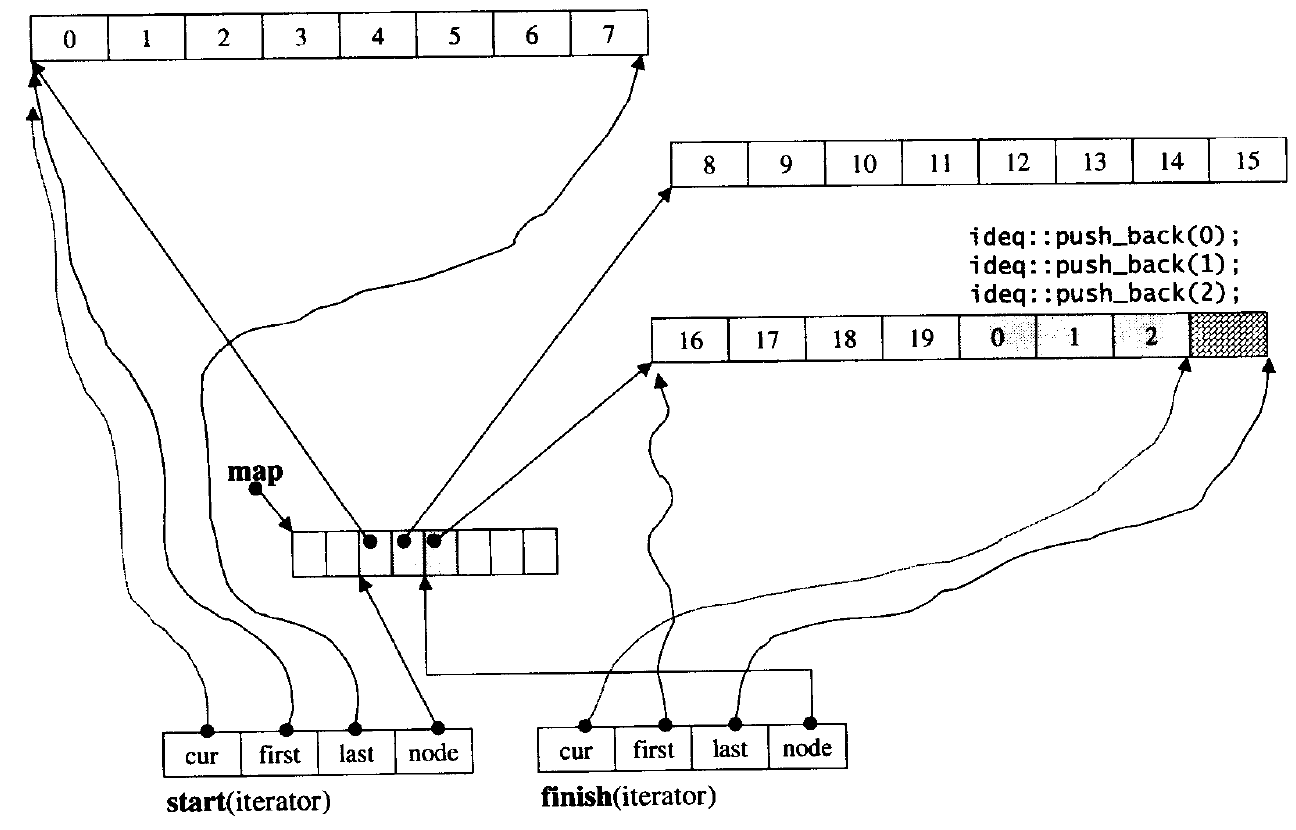从上面的图中可以看出迭代器中node是当前结点，cur指向当前数组位置，用来迭代器访问元素，first和last分别指向每个节点对应的数组的起始位置和末尾。当cur等于last，node就要指向下一个节点，cur又在起始位置了，虽然这些空间不连续，但是可以重载一些函数来定义其行为以及封装看似空间时连续的。
deque的优缺点
优点：与vector比较，deque的优势是：头部插入和删除时，不需要搬移元素，效率特别高，而且在扩容时，也不需要搬移大量的元素，因此其效率是必vector高的。
与list比较，其底层是连续空间，空间利用率比较高，不需要存储额外字段。
缺点：deque有一个致命缺陷：不适合遍历，因为在遍历时，deque的迭代器要频繁的去检测其是否移动到某段小空间的边界，导致效率低下，而序列式场景中，可能需要经常遍历，因此在实际中，需要线性结构
时，大多数情况下优先考虑vector和list，deque的应用并不多，而目前能看到的一个应用就是，STL用其作为stack和queue的底层数据结构。
那么为什么要用deque来作为stack和Queue的默认底层容器呢？
首先stack是一种后进先出的特殊线性数据结构，因此只要具有push_back()和pop_back()操作的线性结构，都可以作为stack的底层容器，比如vector和list都可以；queue是先进先出的特殊线性数据结构，只要具有 push_back和pop_front操作的线性结构，都可以作为queue的底层容器，比如list。
但是STL中对stack和 queue默认选择deque作为其底层容器，主要是因为： 1. stack和queue不需要遍历(因此stack和queue没有迭代器)，只需要在固定的一端或者两端进行操作。 2. 在stack中元素增长时，deque比vector的效率高(扩容时不需要搬移大量数据)；queue中的元素增长 时，deque不仅效率高，而且内存使用率高。 结合了deque的优点，而完美的避开了其缺陷。
栈和队列的模拟实现
在学习C语言阶段，模拟实现了栈和队列，需要的代码量需要几百行，自己造轮子还是比较麻烦的，而在C++中有现成的不需要我们去造轮子，模拟实现栈和队列就轻松多了，deque作为默认的底层容器。
stack代码示例：
template<class T, class Con = deque<T>>class stack{public:void push(const T& x){_c.push_back(x);}void pop(){_c.pop_back();}T& top(){return _c.back();}const T& top()const{return _c.back();}size_t size()const{return _c.size();}bool empty()const{return _c.empty();}private:Con _c;};Queue代码示例：
template<class T, class Con = deque<T>>class queue{public:void push(const T& x){_c.push_back(x);}void pop(){_c.pop_front();}T& back(){return _c.pop_back();}const T& back()const{return _c.pop_back();}T& front(){return _c.front();}const T& front()const{return _c.pop_front();}size_t size()const{return _c.size();}bool empty()const{return _c.empty();}private:Con _c;};优先级队列的模拟实现
优先级队列的底层结构是堆，还是又vector作为容器来实现，而模拟实现优先级队列就需要建堆，在STL中优先级队列默认是大堆，所以在模拟实现中我们也是大堆。在模拟实现的过程中可以发现自己的对知识的疏漏，在建堆和什么时候使用向下调整和向上调整出现了问题，也导致了花费有些时间去复习以前的知识。优先级队列毕竟是队列，还有先进先出的特性，在队列插入元素实在末尾插入，需要根据大小堆来进行向上调整，删除头元素如果直接进行删除就会大大降低效率，可以先和末尾元素交换，接着删除末尾元素，在从根结点开始向下调整，使堆保持大堆或者小堆。
在实现之前需要三个模版参数：
template <class T, class Container = vector<T>, class Compare = less<T> >T是数据的类型，Container是适配器，也就是优先级队列的底层容器，默认容器是vector，compare是仿函数，来控制大堆或者小堆也就是数据的排升降序。注意：这里的less用的是库里面的
变量：
private:Container c;Compare comp;priority_queue初始化
priority_queue(){}template <class InputIterator>priority_queue(InputIterator first, InputIterator last){while (first != last){c.push_back(*first);++first;}for (int i = (size()-2)/2; i >= 0; i--){Adupdown(i);}}构造函数对内置类型不做处理，对于自定义类型会调用自己的构造函数，所以默认构造不需要写，而用迭代器初始化需要建堆，堆的特性使得它能在O(1)时间内获取最高（或最低）优先级的元素，并在O(log n)时间内完成插入和删除操作，这与优先级队列的需求高度契合。堆的结构保证了根节点始终是最大（或最小）元素，每次插入或删除后，堆会通过“上浮”或“下沉”操作重新调整结构，确保优先级顺序始终正确。
向下调整和向上调整算法
void Adupdown(int parent)//向下调整{int child = parent * 2 + 1;while (child < c.size()){if (child + 1 < c.size() && comp(c[child],c[child+1])){child++;}if (comp(c[parent], c[child])){swap(c[parent], c[child]);parent = child;child = parent * 2 + 1;}else{break;}}} void Adjustup(int child)//向上调整{int parent = (child - 1) / 2;while (child > 0){if (comp(c[parent] , c[child])){swap(c[parent], c[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}向下调整通常用于删除堆顶元素或构建堆时,向下调整从根节点开始。向上调整通常用于插入新元素时。将新元素添加到堆的末尾，然后通过向上调整来恢复堆的性质,向上调整从新插入的节点开始。
priority_queue插入和删除
每次插入一个元素就需要向上调整来保持大堆或者小堆，而删除元素也是方便，首位元素进行交换，再删除末尾元素，比直接删除头元素效率更高。
代码示例：
void push(const T& x){c.push_back(x);Adjustup(size() - 1);}void pop(){swap(c[0], c[c.size() - 1]);c.pop_back();Adupdown(0);}priority_queue其它接口
bool empty() const{return c.empty();}size_t size() const{return c.size();}const T& top() const{return c[0];}
对比总结
| 特性 | 双端队列 | 优先级队列 |
|---|---|---|
| 操作位置 | 头部和尾部均支持操作 | 仅支持从优先级最高端操作 |
| 底层实现 | 数组或链表 | 通常为堆（Heap） |
| 时间复杂度 | 插入/删除：O(1)（均摊） | 插入/删除：O(log n) |
| 典型用途 | 双向数据处理、滑动窗口 | 动态优先级任务处理 |