嵌入式学习-（李宏毅）机器学习（5）-day32
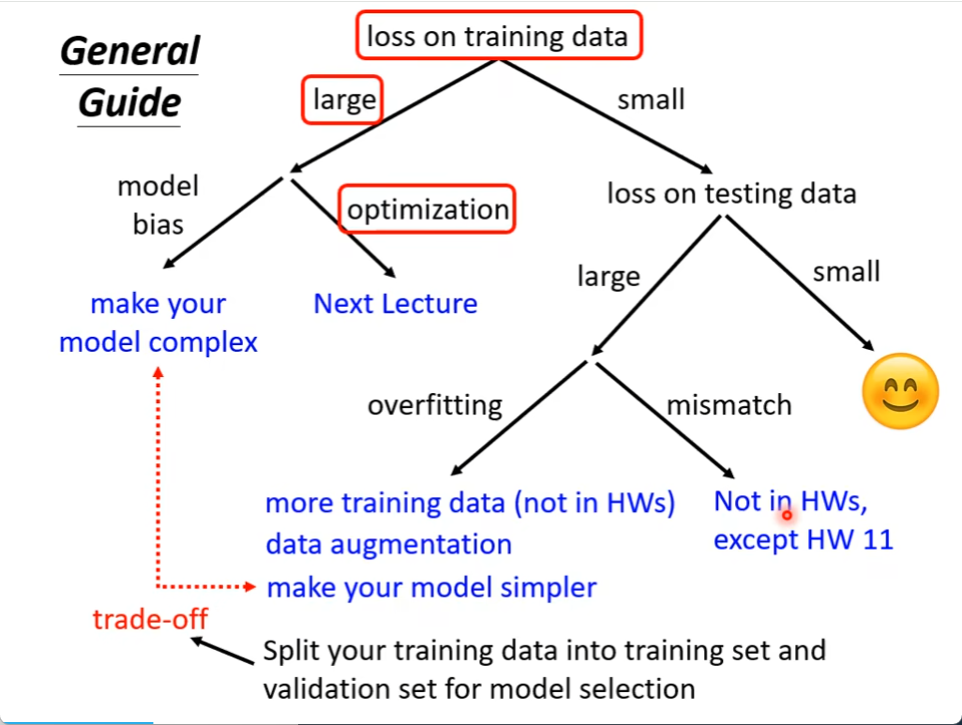如果training 的 loss比较大可能是model bias 也可能是 optimization；如果是model bias，把model变复杂一点，如果是optimization，那就是局部最优解。
如果training的loss小了的话，在看看Testing data 如果Testing data 的loss大的话，那就是overfitting，1，可以增加数据集 2，也可以让模型变得简单一些 3，可以data augmentation（就是用一些对于这个问题的理解，自己创造出一些资料，照片的翻转，截一块下来，不能随便乱做，要做的有道理）4.early stopping 5，less features 6，regularization
限制太多后，就变成了一个直线，这又变成model bias 了
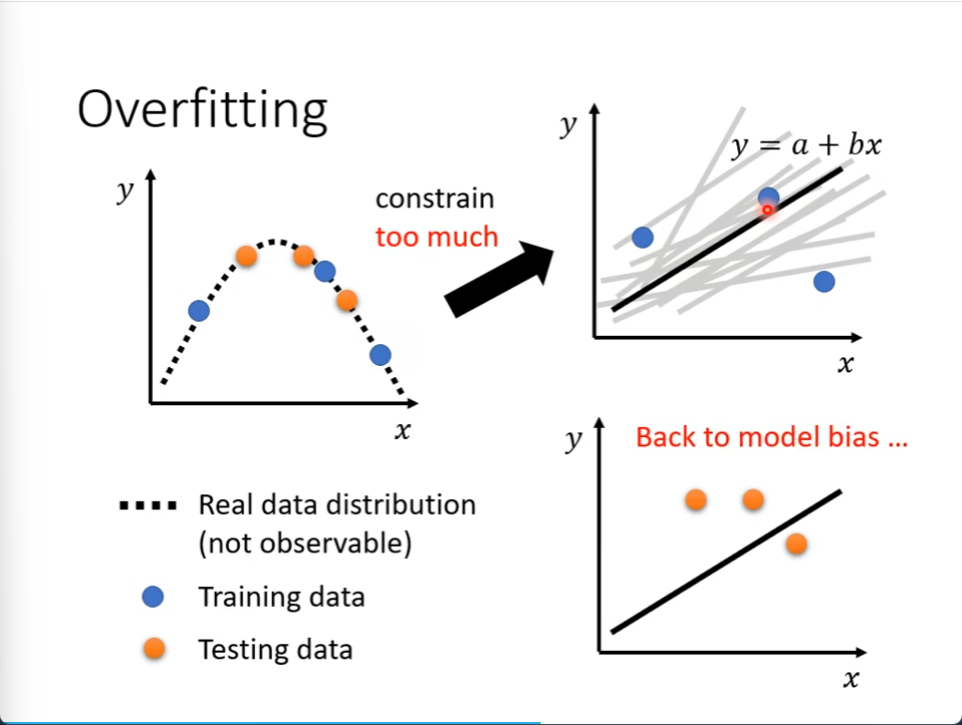
有一点矛盾的地方
蓝线是随着模型复杂程度，模型越复杂，training loss 越低
红显示在Testing loss随着模型越复杂，Testing的loss反而越高
怎么选出中间这个呢
很直觉的是中间那个最好。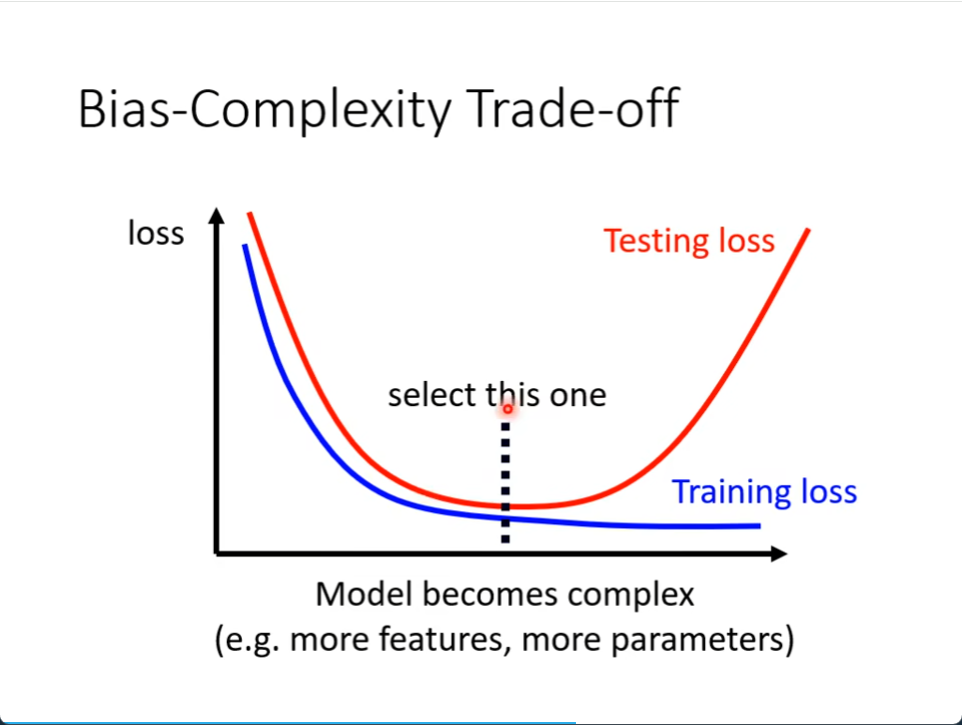
下一节课 optimization
loss不变往往认为微分到0 了
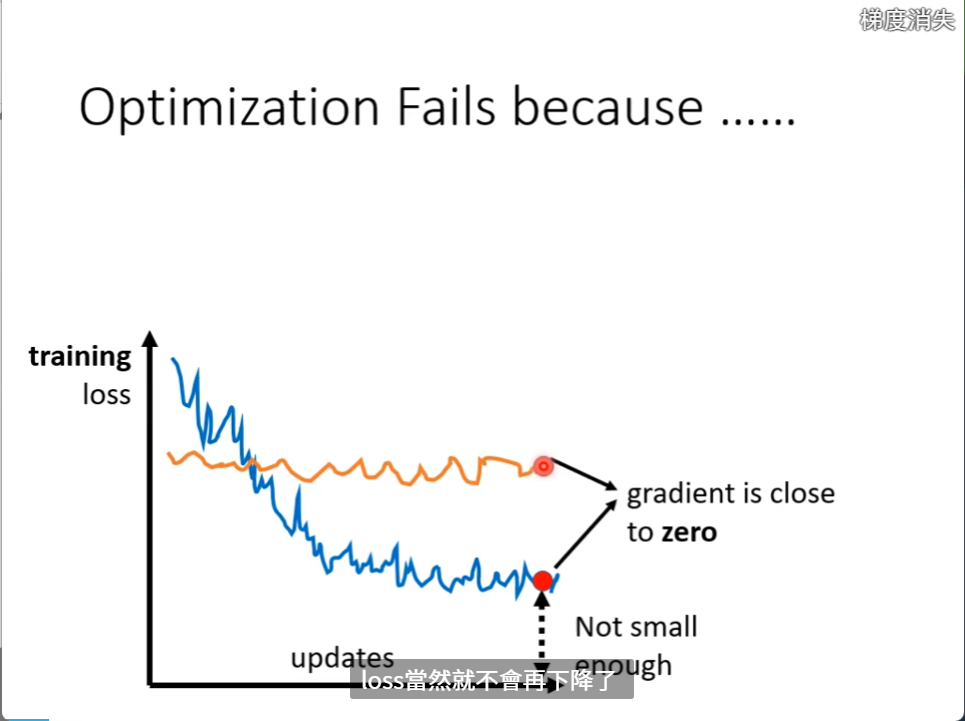
常常是local minima，也有可能是鞍点
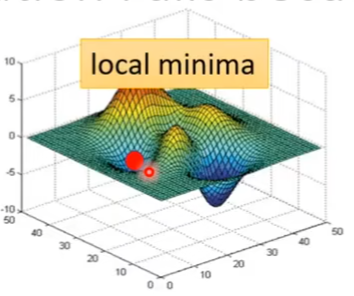
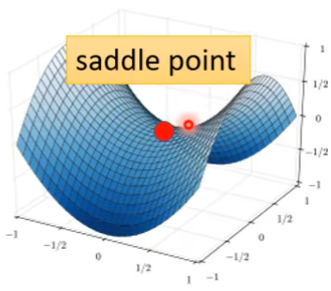
像这些点都叫做critical point
我们有没有办法知道是local minima 还是卡在saddle point
在 saddle point 的话说明还有路可以走的，我们要区分是local minima 还是 saddle point
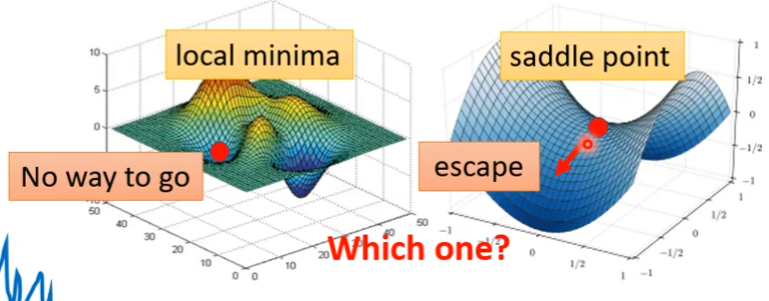
怎么区分呢？用泰勒展开式
还是截图写一下
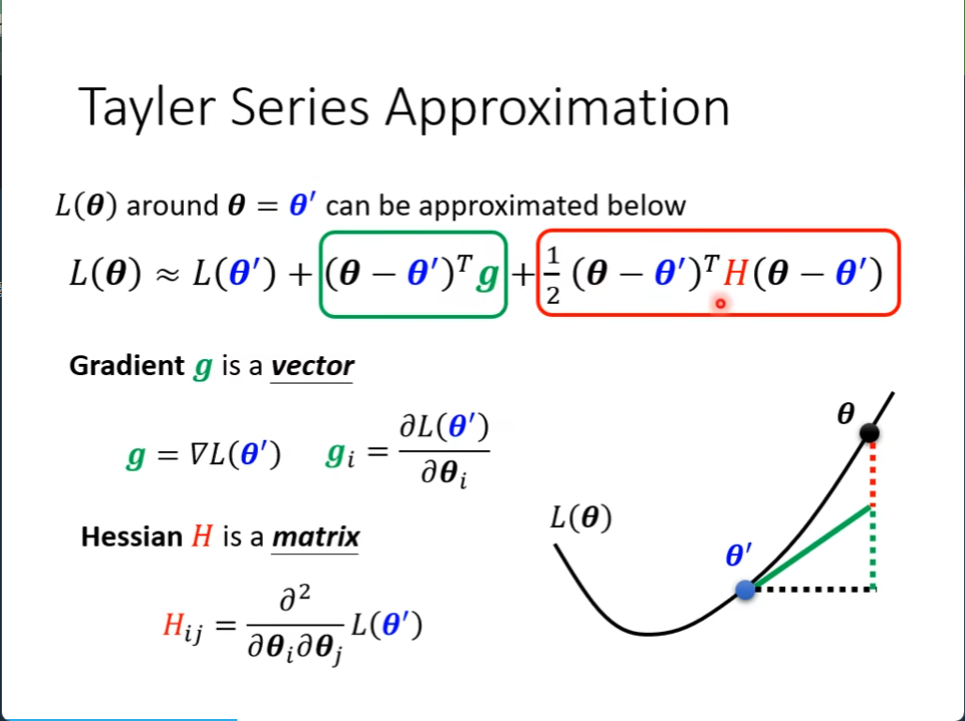
g是一个微分向量，gi就是对setai的微分
（seta-seta撇）转置后乘以g向量
H是一个矩阵，是seta的二次微分（黑塞矩阵）
Hij = 先对i行进行微分后再对j列进行微分
当g为0时，我们可以根据泰勒公式的H来判断是极大值还是极小值还是鞍点
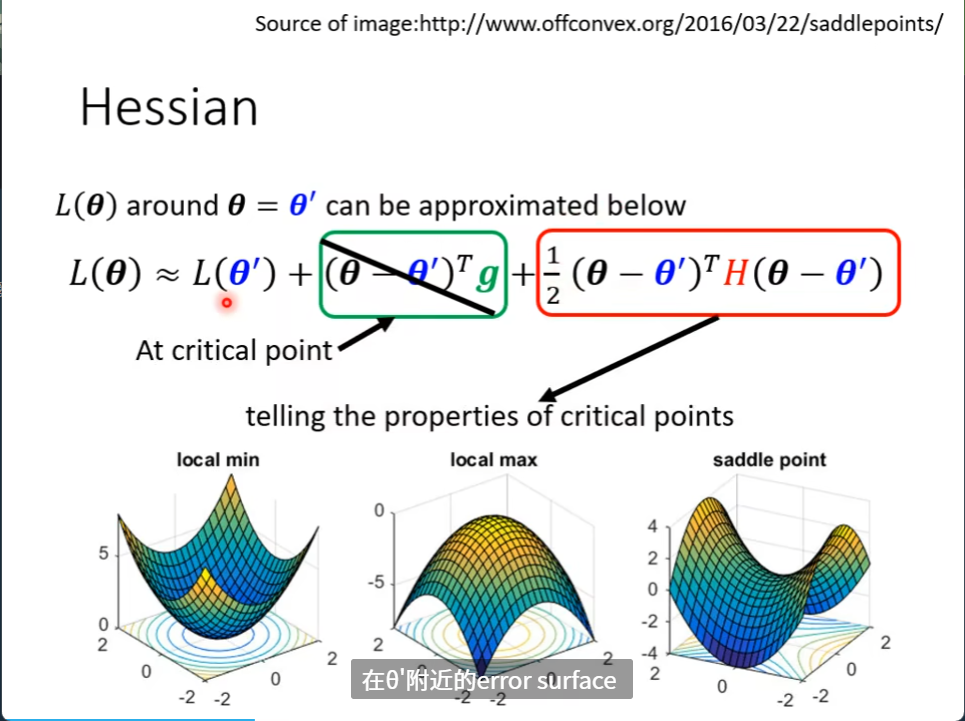
我们怎么可能把所有的V都带进去看呢
我们直接看H的特征值
如果特征值全是正的，那就是local minima
如果特征值全是负的 ，那就是local maxima
如果特征值是有正有负 ，那就是saddle point
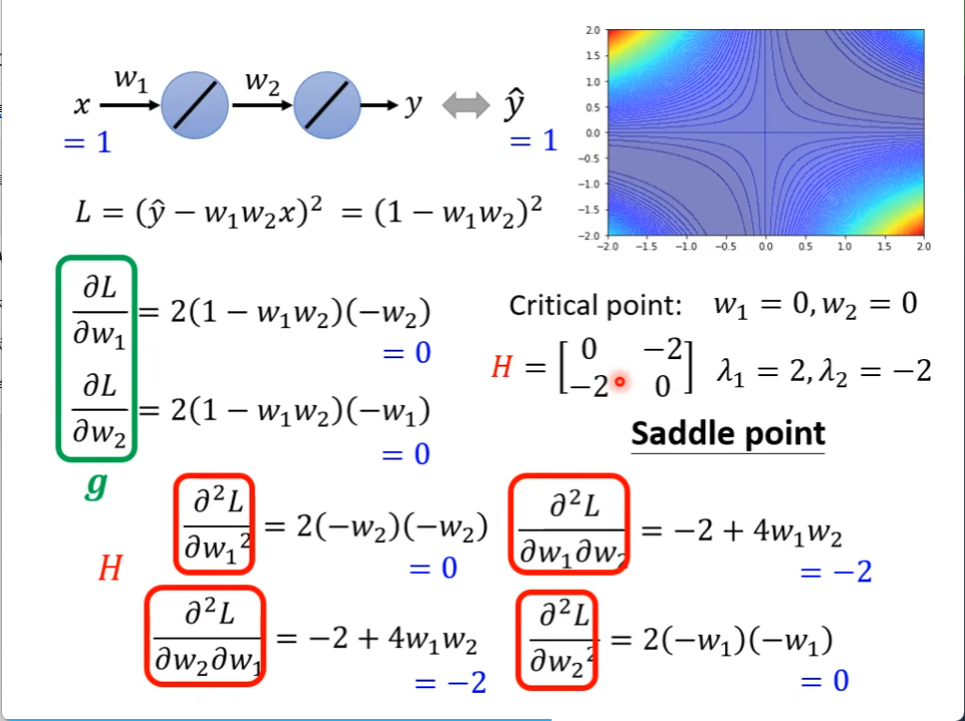
通过算二阶导发现特征值有正有负，那就代表是鞍点，H不光帮我们分辨是不是鞍点，还帮我们找到了update的方向，那就是特征值和特征向量
只要沿着负特征值的特征向量方向，就可以接着decrease L
但是实际上，几乎没有人用这个方法逃离saddle point 因为H矩阵太难求了，况且还要算出特征值特征向量
拿出来讲是因为说 saddle point 不可怕
saddle point 和local minima 哪个更可怕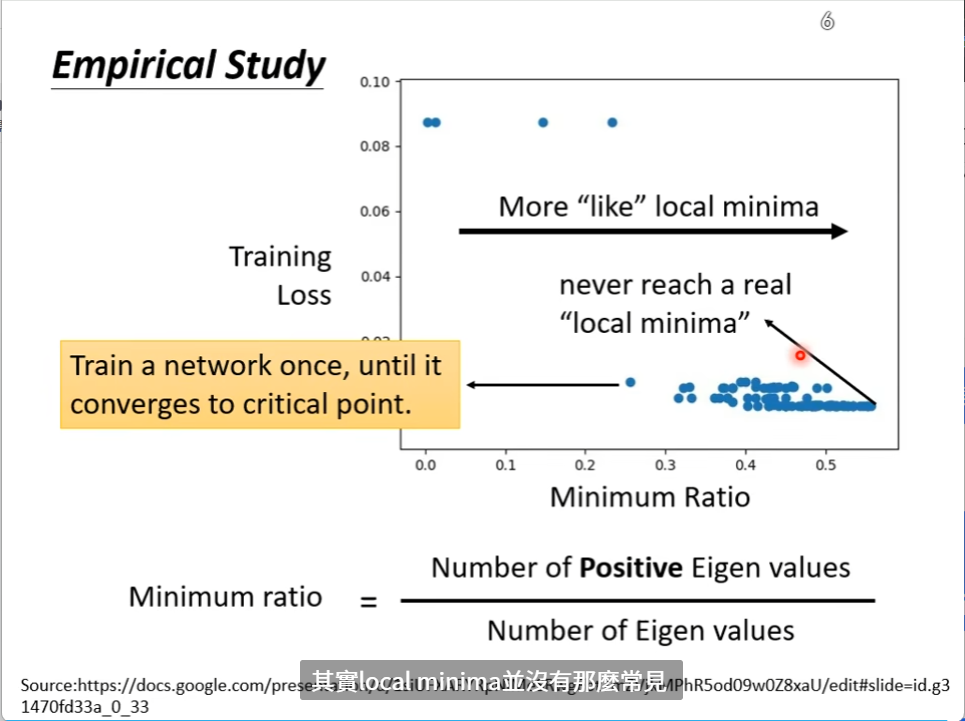
从经验上来讲，local minima没有那么常见，绝大部分都是在saddle point上停住了