当前位置： 首页 > news >正文

力扣刷题日常(11-12)

news 2025/8/3 17:46:01

力扣刷题日常(11-12)

第11题:盛最多水的容器 (难度:中等)

原题:

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明： 我们不能倾斜容器。

示例 1：

img

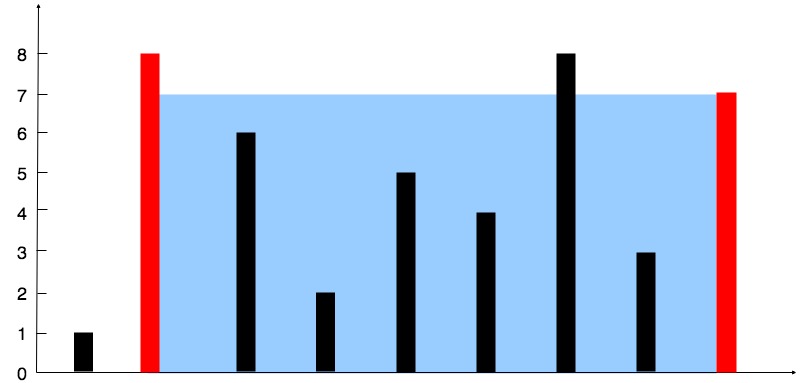
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

  • n == height.length
  • 2 <= n <= 105
  • 0 <= height[i] <= 104

原题提示：

  1. If you simulate the problem, it will be O(n^2) which is not efficient.(如果我们模拟这个问题，其时间复杂度将是 O(n²)，这效率不高。)
  2. Try to use two-pointers. Set one pointer to the left and one to the right of the array. Always move the pointer that points to the lower line.(尽量使用双指针。将一个指针置于数组的左侧，另一个置于右侧。始终移动指向较小值的指针。)
  3. How can you calculate the amount of water at each step?(如何计算每一步的水量？)

开始解题:

这道题的目标是找到两条垂直线,使其与x轴构成的容器能装最多的水.水的容量由两条线中较短的那条(木桶效应)和它们之间的距离共同决定.

  1. 暴力算法的思考

最直观的想法就是尝试所有可能的线段组合.我们可以用一个循环来固定第一条线i,然后用另一个嵌套的循环来遍历所有在i右边的线j.对于每一对(i, j),我们都计算它们能构成的容器容量,然后用一个变量来记录遇到的最大容量.

  • 容量计算公式: area = (j - i) * min(height[i], height[j])
  • j - i 是容器的宽度.
  • min(height[i], height[j]) 是容器的高度,由较短的板决定.

这种方法需要两层循环,时间复杂度是 O(n²).根据题目提示,当n达到105时,n²大约是1010,这个计算量太大了,会导致超时.所以我们需要一个更高效的方法.

  1. 双指针法的优化思路

这正是题目提示我们要使用的核心技巧.双指针法是一种非常高效的线性扫描技巧,它能将时间复杂度降低到 O(n).

我们的核心思路如下:

  1. 初始化: 我们设置两个指针,一个left指向数组的起始位置(索引0),另一个right指向数组的末尾位置(索引n-1).这构成了一个初始的容器,这个容器的宽度是所有可能组合中最大的.

  2. 迭代与移动: 我们在一个循环中持续计算当前left和right指针所构成容器的容量,并更新我们记录的最大容量.然后,关键问题来了: 我们应该移动哪个指针? left向右移,还是right向左移?

    • 让我们再次审视容量公式: 容量 = 宽度 * 高度.
    • 当前容器的宽度是 right - left, 高度是 min(height[left], height[right]).
    • 当我们移动任何一个指针时,无论是left++还是right--,容器的宽度都必然会减小.
    • 因此,要想找到一个比当前容量更大的新容器,我们唯一的希望就是让它的高度增加.

    现在我们来分析移动哪个指针:

    • 假设 height[left] < height[right]. 此时容器的高度由 height[left] (较短的板)决定.
    • 如果我们移动right指针(right--),新的宽度变小了,而新的高度 min(height[left], height[right-1]) 不可能大于 height[left] (因为height[left]仍然是其中一个可能的限制).所以,新的容量新宽度 * 新高度必然小于当前的容量.移动right指针没有任何收益.
    • 反之,如果我们移动left指针(left++),虽然宽度也变小了,但新的高度 min(height[left+1], height[right]) 有可能会大于旧的高度 height[left].这就为我们找到了一个更大容量的容器提供了可能性.

结论: 在每一步,我们都应该移动指向较短垂直线的那一个指针.

算法步骤总结:

  1. 初始化 left = 0, right = height.length - 1, maxArea = 0.
  2. 当 left < right 时,执行循环:
    a. 计算当前宽度 width = right - left.
    b. 确定当前高度 h = min(height[left], height[right]).
    c. 计算当前容量 currentArea = width * h.
    d. 更新最大容量 maxArea = max(maxArea, currentArea).
    e. 比较 height[left] 和 height[right]:
    * 如果 height[left] < height[right], 则 left++.
    * 否则, right--.
  3. 循环结束后,maxArea 就是最终结果.

这种方法,left和right指针总共只会遍历整个数组一次,所以时间复杂度是 O(n),空间复杂度是 O(1).

代码:

public class Solution {public int MaxArea(int[] height) {// 1. 变量声明与初始化int left = 0;int right = height.Length - 1; // 2. 数组属性int maxArea = 0;// 3. while 循环while(left < right){// 4. Math 静态类int h = Math.Min(height[left], height[right]);int width = right - left;int currentArea = width * h;maxArea = Math.Max(maxArea, currentArea);// 5. if-else 条件判断if(height[left] < height[right])left++; // 6. 自增/自减运算符elseright--;}return maxArea;}
}

知识点:

  1. 双指针技巧 (Two-Pointers Technique)

    • 这是一种极其常用且高效的算法技巧,通常用于处理数组或序列问题.它通过维护两个指针在数据结构中移动来减少不必要的计算.
    • 主要类型:
      • 对撞指针(Colliding Pointers): 正如本题所用,一个指针在头,一个在尾,互相靠近.常用于查找满足特定条件的数对.
      • 快慢指针(Fast-Slow Pointers): 两个指针同向移动,但速度不同.常用于判断链表是否有环,或查找链表的中点.
    • 掌握双指针技巧能让我们用 O(n) 的时间解决很多看似需要 O(n²) 才能解决的问题.

  2. 贪心算法思想 (Greedy Algorithm Mindset)

    • 贪心算法的核心是在每一步都做出当前看起来最优的选择,并期望通过一系列局部最优解,最终得到全局最优解.
    • 在本题中,我们的"贪心"选择是: 移动较短的那块板. 我们之所以敢这么做,是因为我们通过推理证明了保留短板并移动长板,绝不可能得到比当前更大的面积.因此,舍弃短板是当前唯一可能找到更优解的策略.
    • 重要提示: 贪心算法并不总是能得到全局最优解,它只适用于具有"贪心选择性质"和"最优子结构"的问题.但它是一种强大的问题解决思路.

练习题:

选择题

对于本题的双指针解法,在 while(left < right) 循环中,为什么我们总是选择移动指向较短垂直线的那个指针?

A. 因为这样可以保证容器的宽度(width)每次都只减少1.
B. 因为移动较长的指针可能会错过最优解,而移动较短的指针则不会.
C. 因为移动较短的指针,下一步才有可能找到一个更高的板来增高容器的高度,从而才有可能得到更大的面积.
D. 因为数组是从小到大排序的.

简答题

请简述暴力解法(O(n²))和双指针解法(O(n))在解决此问题时的主要区别,以及它们各自的优缺点.

参考答案

选择题答案: C
  • A 错误: 无论移动哪个指针,宽度 right - left 每次都减少1.
  • B 错误: 这个说法是结论,但没有解释原因.为什么移动较长的指针会错过最优解?因为它无法让作为瓶颈的短板高度增加.
  • C 正确: 当前容器的面积由 宽度 * 短板高度 决定.当移动指针时,宽度必然减小.要想让新面积有可能超过旧面积,唯一的方法就是期望容器的高度能增加.移动长板,新高度最多和旧短板一样高,面积必然减小.只有移动短板,才有可能遇到一个更高的板,使得新的高度增加,从而弥补宽度的损失,得到更大的面积.
  • D 错误: 题目并未说明数组是排序的.
简答题答案

  • 主要区别:

    • 搜索方式: 暴力解法通过嵌套循环,检查了所有可能的线段组合,是一种无差别的穷举搜索.双指针解法则通过一个巧妙的策略(移动短板),在每一步都排除了大量不可能成为最优解的组合,是一种智能的、收缩范围的搜索.

  • 优缺点:

    • 暴力解法:
      • 优点: 逻辑简单直观,容易理解和实现.
      • 缺点: 时间复杂度为 O(n²),效率极低,当数据规模n很大时,会导致程序超时或卡死.
    • 双指针解法:
      • 优点: 时间复杂度为 O(n),空间复杂度为 O(1),非常高效,能够轻松处理大规模数据.
      • 缺点: 需要对问题进行更深入的分析才能发现其正确性,逻辑上比暴力解法稍复杂.

第12题: 整数转罗马数字 (难度: 中等)

原题：

七个不同的符号代表罗马数字，其值如下：

符号值
I1
V5
X10
L50
C100
D500
M1000

罗马数字是通过添加从最高到最低的小数位值的转换而形成的。将小数位值转换为罗马数字有以下规则：

  • 如果该值不是以 4 或 9 开头，请选择可以从输入中减去的最大值的符号，将该符号附加到结果，减去其值，然后将其余部分转换为罗马数字。
  • 如果该值以 4 或 9 开头，使用 减法形式，表示从以下符号中减去一个符号，例如 4 是 5 (V) 减 1 (I): IV ，9 是 10 (X) 减 1 (I)：IX。仅使用以下减法形式：4 (IV)，9 (IX)，40 (XL)，90 (XC)，400 (CD) 和 900 (CM)。
  • 只有 10 的次方（I, X, C, M）最多可以连续附加 3 次以代表 10 的倍数。我们不能多次附加 5 (V)，50 (L) 或 500 (D)。如果需要将符号附加4次，请使用 减法形式。

给定一个整数，将其转换为罗马数字。

示例 1：

输入： num = 3749

输出： “MMMDCCXLIX”

解释：

3000 = MMM 由于 1000 (M) + 1000 (M) + 1000 (M)700 = DCC 由于 500 (D) + 100 (C) + 100 (C)40 = XL 由于 50 (L) 减 10 (X)9 = IX 由于 10 (X) 减 1 (I)
注意：49 不是 50 (L) 减 1 (I) 因为转换是基于小数位

示例 2：

输入： num = 58

输出：“LVIII”

解释：

50 = L8 = VIII

示例 3：

输入： num = 1994

输出：“MCMXCIV”

解释：

1000 = M900 = CM90 = XC4 = IV

提示：

  • 1 <= num <= 3999

开始解题:

这个问题的核心思想是一种非常直观且强大的算法策略,叫做贪心算法.

想象一下我们在兑换零钱,比如要兑换37元,我们手头有20元,10元,5元,2元,1元的纸币.为了用最少的纸币,我们的直觉会告诉我们:

  1. 先看看能不能用20元的?可以,用一张.还剩17元.
  2. 再看看能不能用20元的?不行了.试试10元的?可以,用一张.还剩7元.
  3. 再看看10元的?不行.试试5元的?可以,用一张.还剩2元.
  4. 再看看5元的?不行.试试2元的?可以,用一张.还剩0元.
  5. 兑换完成.

这个过程就是贪心,即在每一步都做出当前看起来最好的选择.

对于整数转罗马数字,我们也可以采用完全相同的策略.关键在于,我们的"钱币"是什么?

题目给了我们基础的对应关系 (I=1, V=5, X=10等),但更重要的是,它指出了特殊的"减法形式",比如 4 (IV), 9 (IX), 40 (XL), 90 (XC), 400 (CD), 900 (CM).

如果我们把这些特殊形式也看作是"一体"的符号,我们就可以得到一个从大到小的"面值"列表:

值符号
1000M
900CM
500D
400CD
100C
90XC
50L
40XL
10X
9IX
5V
4IV
1I

有了这个列表,我们的贪心策略就非常清晰了:

  1. 初始化: 准备一个空字符串用来拼接结果.
  2. 循环处理: 从列表最大的值(1000)开始,依次尝试从输入的整数 num 中减去它.
  3. 判断与操作:
    • 如果当前的 num 大于或等于列表中的某个值 (比如1000),我们就把这个值对应的罗马符号 (“M”) 添加到结果字符串中,然后从 num 中减去这个值 (1000).
    • 然后,我们继续用当前的 num 和 同一个值 (1000) 进行比较,直到 num 不再大于或等于它.
    • 例如,对于 num = 3749:
      • 3749 >= 1000? 是. 结果: “M”, num 变为 2749.
      • 2749 >= 1000? 是. 结果: “MM”, num 变为 1749.
      • 1749 >= 1000? 是. 结果: “MMM”, num 变为 749.
      • 749 >= 1000? 否. 移动到下一个值 (900).
  4. 迭代: 对列表中的下一个值 (900) 重复第3步.
    • 749 >= 900? 否. 移动到下一个值 (500).
    • 749 >= 500? 是. 结果: “MMMD”, num 变为 249.
    • …以此类推,直到 num 变为 0.

这个过程保证了我们总是优先使用能表示最大数值的符号组合,完美地解决了这个问题.

代码:

public class Solution {public string IntToRoman(int num) {// 1. 定义数值和符号的对应关系, 从大到小排列.// 这种并行的数组结构非常高效, 通过相同的索引(index)来关联值和符号.int[] values = { 1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1 };string[] symbols = { "M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I" };// 2. 使用 StringBuilder 来高效地拼接字符串.StringBuilder result = new StringBuilder();// 3. 遍历所有的数值. 循环条件 `num > 0` 是一个优化, 一旦数字减到0就提前退出循环.for (int i = 0; i < values.Length && num > 0; i++) {// 4. 贪心选择: 只要当前数字还能减去这个值, 就一直减.while (num >= values[i]) {// 减去数值num -= values[i];// 同时拼接上对应的罗马符号result.Append(symbols[i]);}}// 5. 将 StringBuilder 对象转换为最终的 string 并返回.return result.ToString();}
}
部分讲解

StringBuilder 类

  • 是什么: StringBuilder 是一个专门用来处理"可变"字符串的类.
  • 为什么用它: 在C#中, string 类型是不可变的 (immutable). 这意味着每次我们执行 myString = myString + "a"; 这样的操作时, 系统并不是在原来的字符串后面添加字符, 而是创建了一个全新的字符串对象, 然后把旧字符串和 “a” 的内容拷贝进去. 如果在循环中大量执行这种操作(就像本题), 会频繁地创建对象和回收内存, 导致性能下降.
  • StringBuilder 的优势: 它内部维护一个可变的字符缓冲区. 当我们调用 result.Append(symbols[i]); 时, 它只是把新字符添加到缓冲区的末尾, 而不是每次都创建新对象. 这在循环拼接字符串的场景下效率极高.
  • result.ToString(): 当所有拼接操作完成后, 调用 ToString() 方法可以从 StringBuilder 内部的缓冲区生成一个最终的, 不可变的 string 对象.

可能的实际应用:

  1. 贪心算法的应用:

    • 游戏AI: 怪物或NPC的行为决策. 比如一个怪物总是优先攻击离它最近或者血量最低的玩家, 这就是一种贪心策略.
    • 寻路算法: 像A*这样的寻路算法中, "启发函数(heuristic)"部分就带有贪心的思想, 它会估算一个到达终点的"最优"距离, 优先探索看起来离终点更近的节点.
    • 程序化内容生成: 在生成地牢或地图时, 可能会有一个算法贪心地选择下一个房间放置的位置, 以求最快填满空间或连接所有关键点.

  2. 查找表 (Lookup Table) 的应用 (类似本题的values和symbols数组):

    • 游戏数据管理: 在Unity中, 我们可以使用 ScriptableObject 或 Dictionary 创建一个物品ID到物品属性(如名称, 伤害, 图标)的查找表. 当玩家获得ID为101的物品时, 我们可以快速从中查出它的所有信息, 而不是遍历一个巨大的列表.
    • 性能优化: 对于一些计算复杂的函数(比如三角函数), 如果输入值的范围有限, 可以预先计算好一批结果存入数组或哈希表. 在运行时直接查表取值, 用空间换时间, 避免重复的昂贵计算.

  3. StringBuilder 的应用:

    • 动态UI文本: 构建复杂的UI显示内容, 比如一个角色的状态面板, 需要拼接玩家姓名, 等级, 生命值, 魔法值, 各种状态效果等多个信息.
    • 日志系统: 在开发过程中, 我们可能需要一个日志系统来记录游戏运行时的详细信息. 将多条日志信息拼接成一个完整的日志文件时, 使用 StringBuilder 会比用 + 高效得多.
    • 数据序列化: 当我们需要将游戏存档数据转换成JSON或XML格式的字符串时, 这个过程涉及到大量的字符串拼接, StringBuilder 是不二之选.
http://www.dtcms.com/a/312245.html

相关文章：

  • linux编译基础知识-头文件标准路径
  • NX947NX955美光固态闪存NX962NX966
  • FreeRTOS源码分析二：task启动（RISCV架构）
  • 8.苹果ios逆向-安装frida
  • DBMS设计 之1 从DBMS 到数据中台
  • C语言-指针初级（指针定义、指针的作用、指针的计算、野指针、悬空指针、void类型指针）
  • Spring框架深度学习实战
  • ⭐CVPR2025 单目视频深度估计新框架 Seurat
  • 嵌入式系统的中断控制器（NVIC）
  • rosdep的作用以及rosdep install时的常用参数
  • 质数时间（二分查找）
  • ​​​​​​​第二十一天（CDN绕过）
  • EPICS aSub记录示例2
  • [学习笔记-AI基础篇]02_深度基础
  • Kotlin协程极简教程：5分钟学完关键知识点
  • 工业场景工服识别准确率↑32%：陌讯多模态融合算法实战解析
  • OpenVLA复现
  • 23th Day| 39.组合总和,40.组合总和II,131.分割回文串
  • Linux—进程状态
  • 深入 Go 底层原理（九）：context 包的设计哲学与实现
  • 智能手表：电源检查
  • Java多线程详解（2）
  • 一、灵巧手捉取几何原理——空间五指平衡捉取
  • GraphRag安装过程中的报错：系统找不到指定的文件(Could not install packages due to an OSError)
  • AI赋能测试：技术变革与应用展望
  • C++const成员
  • [网安工具] Web 漏洞扫描工具 —— AWVS · 使用手册
  • 机器学习【五】decision_making tree
  • Linux重定向和缓冲区
  • Piriority_queue