[学习笔记-AI基础篇]02_深度基础

[学习笔记-AI基础篇]02_深度学习基础

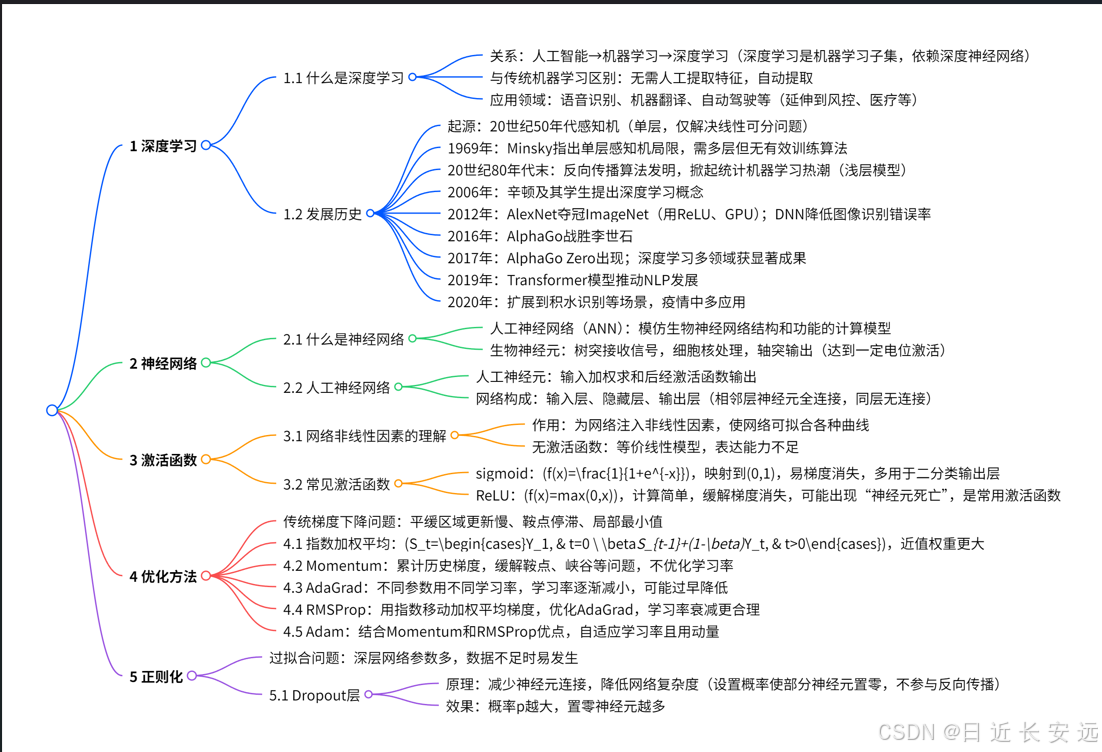
人工智能，机器学习和深度学习之间的关系：

传统机器学习算术依赖⼈⼯设计特征，并进⾏特征提取，⽽深度学习⽅法不需要⼈⼯，⽽是依赖算法⾃动提取特征。深度学习模仿⼈类⼤脑的运⾏⽅式，从经验中学习获取知识。这也是深度学习被看做⿊盒⼦，可解释性差的原因。 随着计算机软硬件的⻜速发展，现阶段通过深度学习来模拟⼈脑来解释数据，包括图像，⽂本，⾳频等内容。⽬前 深度学习的主要应⽤领域有： 1. 语⾳识别 2. 机器翻译 3. ⾃动驾驶 当然在其他领域也能⻅到深度学习的身影，⽐如⻛控，安防，智能零售，医疗领域，推荐系统等

人工提取特征+模型自动分类  VS 模型和神经网络的自动完成特征提取和分类。

什么是神经⽹络？

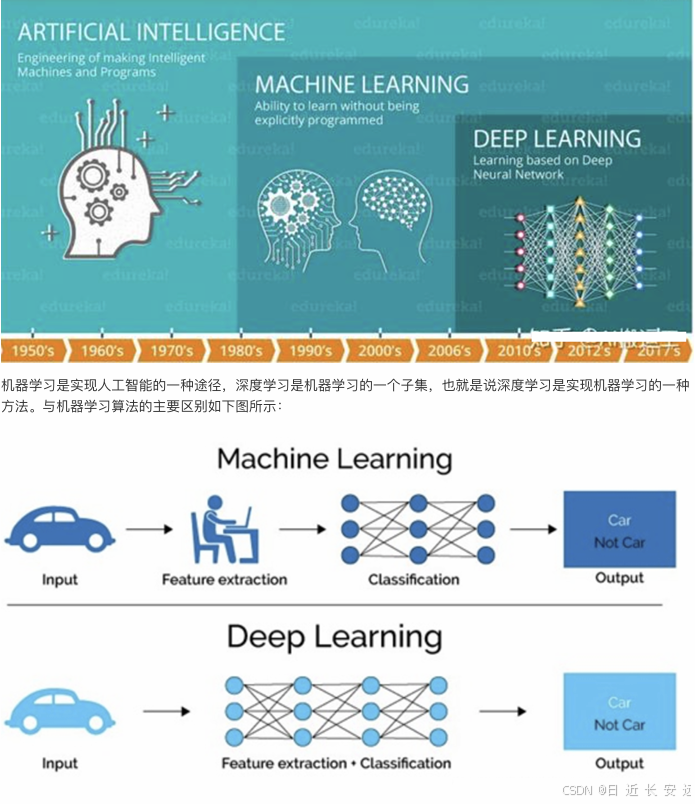
⼈⼯神经⽹络（ Artificial Neural Network， 简写为ANN）也简称为神经⽹络（NN），是⼀种模仿⽣物神经⽹络 结构和功能的 计算模型。⼈脑可以看做是⼀个⽣物神经⽹络，由众多的神经元连接⽽成。各个神经元传递复杂的电 信号，树突接收到输⼊信号，然后对信号进⾏处理，通过轴突输出信号。下图是⽣物神经元示意图：当电信号通过树突进⼊到细胞核时，会逐渐聚集电荷。达到⼀定的电位后，细胞就会被激活，通过轴突发出电信号。

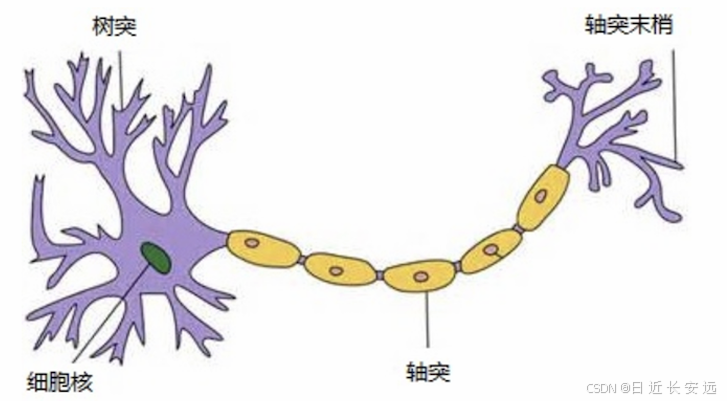
⼈⼯神经⽹络

构建⼈⼯神经⽹络中的神经元

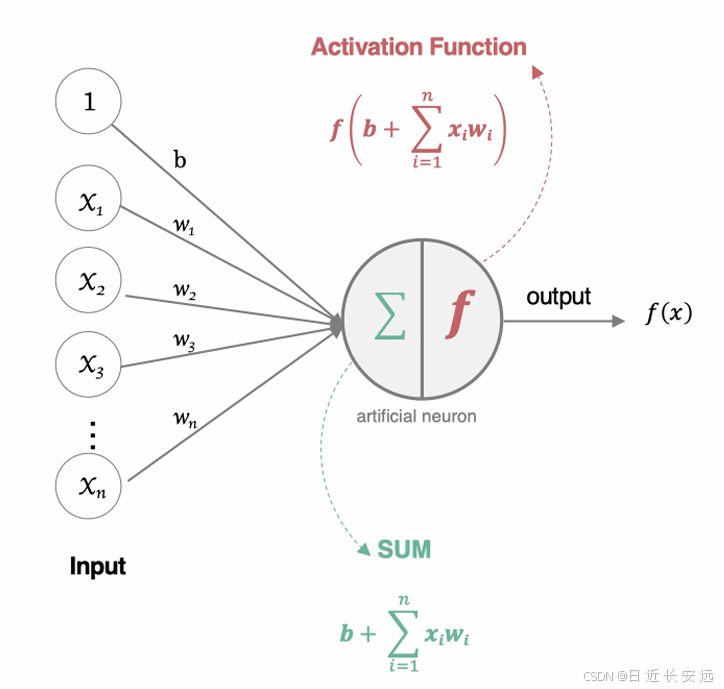
这个流程就像，来源不同树突(树突都会有不同的权重)的信息, 进⾏的加权计算, 输⼊到细胞中做加和，再通过激活函数输出 细胞值

使⽤多个神经元来构建神经⽹络，相邻层之间的神经元相互连接，并给每⼀个连接分配⼀个强度，如 下图所示：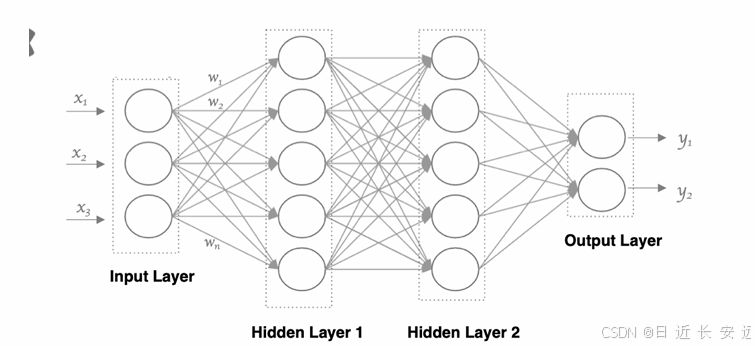

神经⽹络中信息只向⼀个⽅向移动，即从输⼊节点向前移动，通过隐藏节点，再向输出节点移动。其中的基本部分 是:

1. 输⼊层: 即输⼊ x 的那⼀层

2. 输出层: 即输出 y 的那⼀层

3. 隐藏层: 输⼊层和输出层之间都是隐藏层

特点是： 同⼀层的神经元之间没有连接。 第 N 层的每个神经元和第 N-1层 的所有神经元相连（这就是full connected的含义), 第N-1层神经元的输出就是第N 层神经元的输⼊。每个连接都有⼀个权值。

激活函数

⽹络⾮线性因素的理解：

激活函数⽤于对每层的输出数据进⾏变换, 进⽽为整个⽹络结构结构注⼊了⾮线性因素。此时, 神经⽹络就可以拟合各种曲线。如果不使⽤激活函数，整个⽹络虽然看起来复杂，其本质还相当于⼀种线性模型

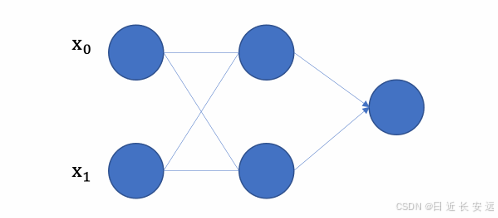
1.没有引⼊⾮线性因素的⽹络等价于使⽤⼀个线性模型来拟合；；

2. 通过给⽹络输出增加激活函数, 实现引⼊⾮线性因素, 使得⽹络模型可以逼近任意函数, 提升⽹络对复杂问题的拟合能⼒

常⻅的激活函数：

激活函数主要⽤来向神经⽹络中加⼊⾮线性因素, 以解决线性模型表达能⼒不⾜的问题, 它对神经⽹络有着极其重要 的作⽤。我们的⽹络参数在更新时, 使⽤的反向传播算法(BP), 这就要求我们的激活函数必须可微

sigmoid 激活函数：

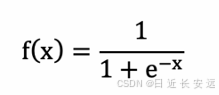
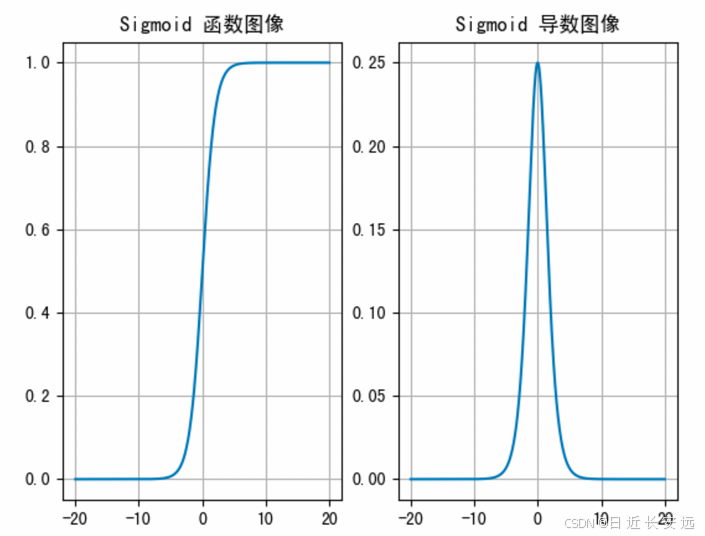
从 sigmoid 函数图像可以得到，sigmoid 函数可以将任意的输⼊映射到 (0, 1) 之间，当输⼊的值⼤致在-6 时，意味着输⼊任何值得到的激活值都是差不多的，这样会丢失部分的信息。⽐如：输⼊ 100 和输出 10000 经过 sigmoid 的激活值⼏乎都是等于 1 的，但是输⼊的数据之间相差 100 倍的信息就丢失了。

对于 sigmoid 函数⽽⾔，输⼊值在 [-6, 6] 之间输出值才会有明显差异，输⼊值在 [-3, 3] 之间才会有⽐较好的效果。

通过上述导数图像，我们发现导数数值范围是 (0, 0.25)，当输⼊ <-6 或者>6时，sigmoid 激活函数图像的导数接近为 0，此时⽹络参数将更新极其缓慢，或者⽆法更新。（即模型无法训练，无法收敛）

⼀般来说， sigmoid ⽹络在 5 层之内就会产⽣梯度消失现象。⽽且，该激活函数并不是以 0 为中⼼的，所以在实践中这种激活函数使⽤的很少。sigmoid函数⼀般只⽤于⼆分类的输出层。

ReLU 激活函数

AlexNet夺冠ImageNet（用ReLU、GPU）；DNN降低图像识别错误率

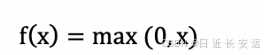
图像：

从上述函数图像可知，ReLU 激活函数将⼩于 0 的值映射为 0，⽽⼤于 0 的值则保持不变，它更加重视正信号，⽽ 忽略负信号，这种激活函数运算更为简单，能够提⾼模型的训练效率。

但是，如果我们⽹络的参数采⽤随机初始化时，很多参数可能为负数，这就使得输⼊的正值(负数)会被舍去，⽽输⼊的负值则会保留，这可能在⼤部分的情况下并不是我们想要的结果。

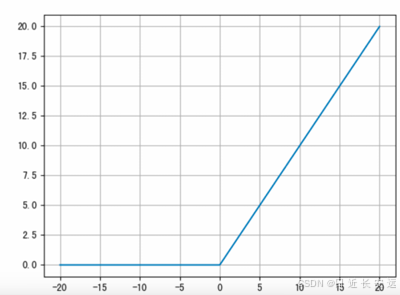
导数函数：

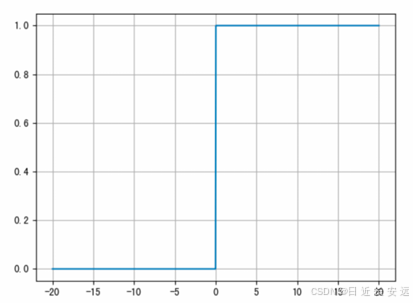
ReLU是⽬前最常⽤的激活函数。 从图中可以看到，当x<0时，ReLU导数为0;⽽当x>0时，则不存在饱和问题。所 以，ReLU 能够在x>0时保持梯度不衰减，从⽽缓解梯度消失问题。然⽽，随着训练的推进，部分输⼊会落⼊⼩于0 区域，导致对应权重⽆法更新。这种现象被称为“神经元死亡”

与sigmoid相⽐，RELU的优势是：

采⽤sigmoid函数，计算量⼤（指数运算），反向传播求误差梯度时，求导涉及除法，计算量相对⼤，⽽采⽤Relu 激活函数，整个过程的计算量节省很多。

sigmoid函数反向传播时，很容易就会出现梯度消失的情况，从⽽⽆法完成深层⽹络的训练。

Relu会使⼀部分神经元的输出为0，这样就造成了⽹络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合 问题的发⽣。

梯度下降优化算法

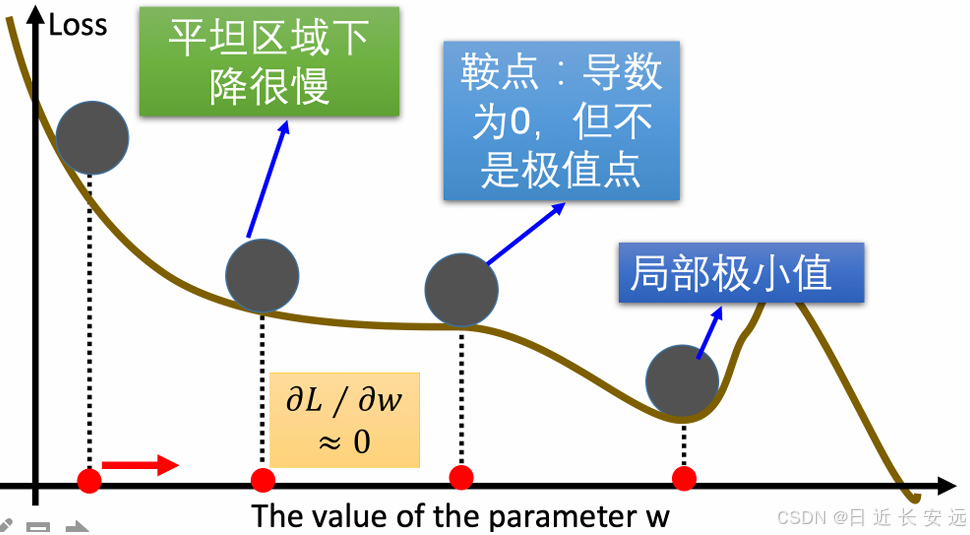
传统的梯度下降优化算法中，可能会碰到以下情况：

碰到平缓区域，梯度值较⼩，参数优化变慢;碰到 “鞍点” ，梯度为 0，参数⽆法优化;碰到局部最⼩值

对于这些问题, 出现了⼀些对梯度下降算法的优化⽅法，例如：Momentum、AdaGrad、RMSprop、 Adam 等

指数加权平均:

我们最常⻅的算数平均指的是将所有数加起来除以数的个数，每个数的权重是相同的。

加权平均指的是给每个数赋予不同的权重求得平均数。

移动平均数，指的是计算最近邻的 N 个数来获得平均数。

指数移动加权平均则是参考各数值，并且各数值的权重都不同，距离越远的数字对平均数计算的贡献就越⼩ （权重较⼩），距离越近则对平均数的计算贡献就越⼤（权重越⼤）。 人话理解：明天⽓温怎么样，和昨天⽓温有很⼤关系，⽽和⼀个⽉前的⽓温关系就⼩⼀些

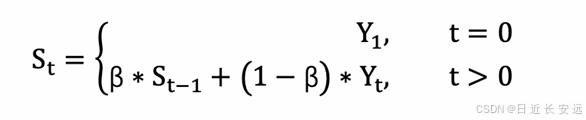
1. St 表示指数加权平均值; 2. Yt 表示 t 时刻的值; 3. β 调节权重系数，该值越⼤平均数越平缓。

Momentum

当梯度下降碰到 “峡⾕” 、”平缓”、”鞍点” 区域时, 参数更新速度变慢. Momentum 通过指数加权平均法，累计历史梯度值，进⾏参数更新，越近的梯度值对当前参数更新的重要性越⼤

梯度计算公式：Dt = β * St-1 + (1- β) * Dt

St-1 表示历史梯度移动加权平均值； wt 表示当前时刻的梯度值； β 为权重系数

Monmentum 优化⽅法是如何⼀定程度上克服 “平缓”、”鞍点”、”峡⾕” 的问题呢？

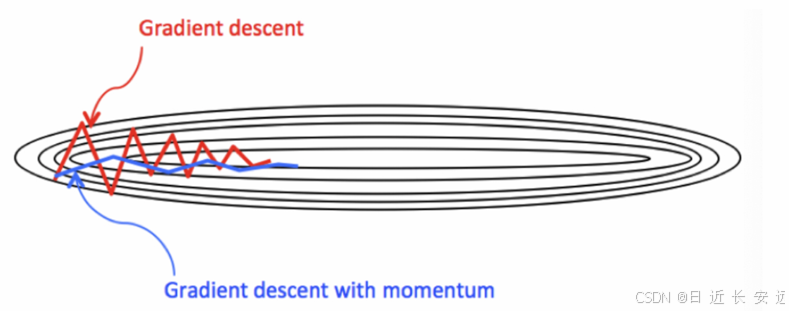
当处于鞍点位置时，由于当前的梯度为 0，参数⽆法更新。但是 Momentum 动量梯度下降算法已经在先前积累了⼀些梯度值(St-1)，很有可能使得跨过鞍点。

由于 mini-batch 普通的梯度下降算法，每次选取少数的样本梯度确定前进⽅向，可能会出现震荡，使得训练时间变⻓。Momentum 使⽤移动加权平均，平滑了梯度的变化，使得前进⽅向更加平缓，有利于加快训练过程。⼀定程度上有利于降低 “峡⾕” 问题的影响。

峡⾕问题：就是会使得参数更新出现剧烈震荡. Momentum 算法可以理解为是对梯度值的⼀种调整，我们知道梯度下降算法中还有⼀个很重要的学习率， Momentum 并没有学习率进⾏优化!

AdaGrad

AdaGrad 通过对不同的参数分量使⽤不同的学习率，AdaGrad 的学习率总体会逐渐减⼩，这是因为 AdaGrad 认为：在起初时，我们距离最优⽬标仍较远，可以使⽤较⼤的学习率，加快训练速度，随着迭代次数的增加，学习率逐渐下降。

其计算步骤如下： 初始化学习率 α、初始化参数 θ、⼩常数 σ = 1e-6

初始化梯度累积变量 s = 0

从训练集中采样 m 个样本的⼩批量，计算梯度 g

累积平⽅梯度 s = s + g ⊙ g，⊙ 表示各个分量相乘

学习率 α 的计算公式如下

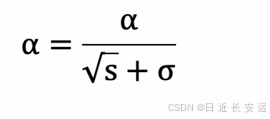
参数更新公式如下：

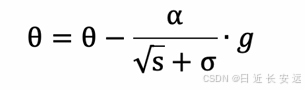
重复上述步骤.

AdaGrad 缺点是可能会使得学习率过早、过量的降低，导致模型训练后期学习率太⼩，较难找到最优解。

RMSProp

RMSProp 优化算法是对 AdaGrad 的优化. 最主要的不同是，其使⽤指数移动加权平均梯度替换历史梯度的平⽅和。其计算过程如下:

1. 初始化学习率 α、初始化参数 θ、⼩常数 σ = 1e-6

2. 初始化参数 θ

3. 初始化梯度累计变量 s

4. 从训练集中采样 m 个样本的⼩批量，计算梯度 g

5. 使⽤指数移动平均累积历史梯度，公式如下:

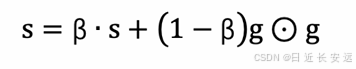
学习率 α 的计算公式如下：

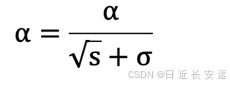
参数更新公式如下

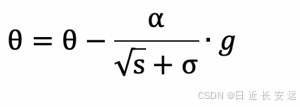
RMSProp 与 AdaGrad 最⼤的区别是对梯度的累积⽅式不同，对于每个梯度分量仍然使⽤不同的学习率。

RMSProp 通过引⼊衰减系数 β，控制历史梯度对历史梯度信息获取的多少. 被证明在神经⽹络⾮凸条件下的优化更好，学习率衰减更加合理⼀些。

需要注意的是：AdaGrad 和 RMSProp 都是对于不同的参数分量使⽤不同的学习率，如果某个参数分量的梯度值较⼤，则对应的学习率就会较⼩，如果某个参数分量的梯度较⼩，则对应的学习率就会较⼤⼀些

Adam(集大成)

Momentum 使⽤指数加权平均计算当前的梯度值、AdaGrad、RMSProp 使⽤⾃适应的学习率，Adam 结合 了 Momentum、RMSProp 的优点，使⽤：移动加权平均的梯度和移动加权平均的学习率。使得能够⾃适应 学习率的同时，也能够使⽤ Momentum 的优点

正则化

在训深层练神经⽹络时，由于模型参数较多，在数据量不⾜的情况下，很容易过拟合。Dropout 就是在神经 ⽹络中⼀种缓解过拟合的⽅法

Dropout 层的原理和使⽤

我们知道，缓解过拟合的⽅式就是降低模型的复杂度，⽽ Dropout 就是通过减少神经元之间的连接，把稠密的神经⽹络神经元连接，变成稀疏的神经元连接，从⽽达到降低⽹络复杂度的⽬的。 我们先通过⼀段代码观察下丢弃层的效果：

import torchimport torch.nn as nndef test():# 初始化丢弃层,0.8即丢失百分之八十
dropout = nn.Dropout(p=0.8)# 初始化输⼊数据
inputs = torch.randint(0, 10, size=[5, 8]).float()print(inputs)print('-' * 50)outputs = dropout(inputs)print(outputs)if __name__ == '__main__':test()

tensor([[1., 0., 3., 6., 7., 7., 5., 7.],[6., 8., 4., 6., 2., 0., 4., 1.],[1., 4., 6., 9., 3., 1., 2., 1.],[0., 6., 3., 7., 1., 7., 8., 9.],[5., 6., 8., 4., 1., 7., 5., 5.]])
-------------------------------------------------
tensor([[ 0.,  0., 15.,  0.,  0.,  0.,  0.,  0.],[ 0.,  0.,  0.,  0., 10.,  0.,  0.,  0.],[  0.,  0.,  0., 45.,  0.,  0.,  0.,  0.],[ 0.,  0., 15.,  0.,  0.,  0.,  0.,  0.],[ 25.,  0.,  0.,  0.,  0.,  0.,  0., 25.]])

我们将 Dropout 层的概率 p 设置为 0.8，此时经过 Dropout 层计算的张量中就出现了很多 0 , 概率 p 设置值 越⼤，则张量中出现的 0 就越多。

当张量某些元素被设置为 0 时, 对⽹络会带来什么影响? 被置零的神经元将⽆法参与反向传播与梯度更新, 相当于是"死节点"!!

人话：神经网络 拟合的能力太强 可以把大量的信息拟合进来，为了不难么强大，所以才这样让一些链接失效。