ART数据库索引结构--ART,The adaptive radix tree论文细读
ART数据库索引结构--ART,The adaptive radix tree论文细读
- 自适应的节点设计:
- 叶子节点设计:
- 合并内部节点(collapsing inner nodes)
- 算法部分
- 搜索
- 插入
- 空间消耗
- 构造二进制可比较的键
- 定义
- 解释
- B. Transformations
- 比较
- 未来展望
前缀树就不过多涉及,比较简单理解,就是取一个key的一部分作为一个节点,比如key=“APPLE”,那么节点就是
A->P->P->L->E
其中在E的地方并没有直接存储value,而是在E对应的节点数组相同位置存储value数组中通过E的索引寻找value。
自适应的节点设计:

叶子节点设计:
- Single-value leaves(单值叶子节点)
这类叶子节点专门用来存储一个单独的值。这种叶子节点是独立的一种节点类型,结构简单,只存一个值。适合场景:某个key对应的value就是一个单一的实体。
2. Multi-value leaves(多值叶子节点)
有些key可能对应多个值,或者需要更复杂的存储结构。多值叶子节点借鉴了内部节点的结构:它们不存指针,而是存储值,但结构类似内部节点。ART中有4种不同的多值叶子节点类型(对应内部节点的4种类型:Node4, Node16, Node48, Node256),区别在于存的是值而非指针。
这样设计方便扩展和管理多个值。
- Combined pointer/value slots(指针和值合并存储)
如果值的大小能“塞进”指针的存储空间(比如64位指针,值是小整数或可用指针tag技术编码的内容),那么就可以用同一个存储单元存指针或值。不需要为值单独创建叶子节点。通过额外的一位bit或者**指针标记(pointer tagging)**技术区分这个存储是指针还是值。这样设计节省内存,提高查找效率。
| 方法 | 支持可变长key | 查找路径长度 | 实现复杂度 | 适用场景 |
|---|---|---|---|---|
| Single-value leaves | 支持 | 较长 | 简单 | 通用,键值长度不定的场景 |
| Multi-value leaves | 不支持 | 较短 | 中等 | 所有key长度相同的应用 |
| Combined pointer/value slots | 支持 | 较短 | 复杂 | 高性能场景,如数据库二级索引 |
合并内部节点(collapsing inner nodes)
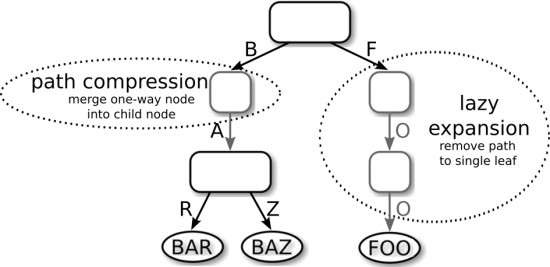
第一种技术是 延迟展开(lazy expansion):只有当内部节点必须区分至少两个叶子节点时,才创建该内部节点。图6展示了一个例子,延迟展开通过截断指向叶子“FOO”的路径,节省了两个内部节点。当插入另一个以“F”为前缀的叶子时,这条路径才会被展开。由于路径可能被截断,这种优化要求在叶子节点存储完整键,或者能从数据库中获取完整键,以便还原路径。
第二种技术是路径压缩(Path compression):路径压缩是指删除所有只有一个子节点的内部节点,以缩短树的高度,节省空间。举例来说,在图6中,存储部分键 ‘A’ 的那个内部节点被删除了。但这个被删除的部分键不能简单忽略掉,必须有办法在查找时处理它。对此,有两种常用方法:
- 悲观策略(Pessimistic)
在每个内部节点存储一个可变长度的部分键向量(可能为空)。这个向量包含了所有被删除的单子节点对应的键片段。查找时,在进入下一个子节点前,需要将这个部分键向量与查询键进行比较,确认路径正确。
- 乐观策略(Optimistic)
只存储被删除单子节点的数量(即向量长度),不存实际部分键。查找时直接跳过相应长度的字节,不做比较。但在到达叶子节点时,必须将叶子节点的完整键与查询键进行对比,确保没有走错路径。
这两种策略的权衡:两者都保证每个内部节点至少有两个子节点。乐观策略对长字符串特别有利,因为查找时省去了中间的比较,但需要在叶子节点做额外一次完整对比。悲观策略则需要更多空间,节点大小不固定,容易造成内存碎片。
文章采用的折中方案
每个节点都存储一个固定大小的部分键向量(8字节),类似悲观策略,但大小固定。如果实际需要存储的部分键超过8字节,查找算法会动态切换到乐观策略。这样既避免了额外检查的开销,也减少了内存浪费和碎片问题。
算法部分
搜索

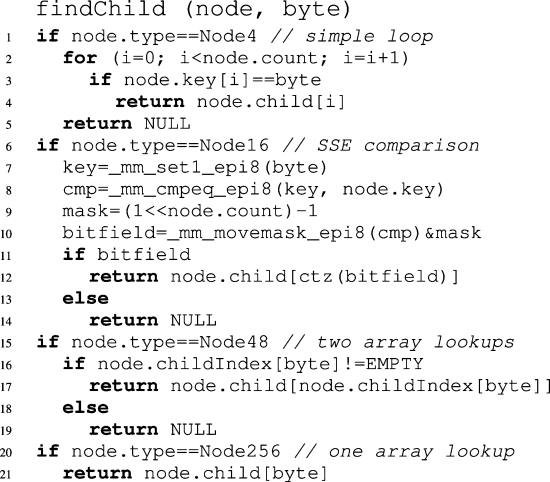
伪代码上图所示。搜索过程是:
通过依次访问key的每个字节,沿树往下遍历。
直到遇到叶子节点或者空指针(null pointer)停止。
关键点解析
- 第4行 处理了 延迟展开(lazy expansion): 检查遇到的叶子节点是否与整个key完全匹配,不匹配则终止搜索。
- 第7和8行处理 悲观路径压缩(pessimistic path compression): 如果压缩路径与key不匹配,则终止搜索。
- findChild函数(第二张图) 负责在内部节点中找到对应的子节点。
不同节点类型的查找实现
- Node4(节点最多4个子节点):用简单循环遍历所有键来匹配。
- Node16(节点最多16个子节点):伪代码使用了SIMD指令(SSE)实现并行比较:
先将查询字节复制成16份(line 7)
再用一条指令并行比较这16个存储的键(line 8)
创建掩码(mask),因为有效条目可能少于16个(line 9)
将比较结果转成位字段(bit field),并应用掩码(line 10)
用“count trailing zero”指令将位字段转成索引(line 12)
如果没有SIMD支持,也可以用二分查找代替。
- Node48(节点最多48个子节点):先检查 childIndex 中对应的条目是否有效,再返回对应指针。
- Node256(节点最多256个子节点):直接通过数组索引访问对应子节点指针,查找效率最高。
其中prefixLen是压缩节点中的重复前缀长度。顺便解释一下参数含义:
**node:**当前正在处理的 树节点(可以是内部节点、叶子节点,也可能是 nullptr)。递归调用时,每深入一层,就把当前的 node 换成它的某个子节点。
**key:**要查找或插入的 完整键。在实现里一般是一个字节数组(uint8_t *)或者字符串。在 ART 中,key 本身不会被“切掉”传下去,而是始终是完整的,结合 depth 决定当前匹配的位置。
**depth:**当前处理到的 key 的第几个字节(从 0 开始)。表示在递归过程中,已经匹配了多少个字节。在下一次递归时,会 depth + 1,表示往下匹配下一个字节。如果节点有压缩路径(prefix),depth 会一次性加上 prefixLen。
重新整理下搜索的伪代码:
search(node, key, depth):if node is null → not foundif node is leaf → 比较叶子的完整key与传入的keyif node has prefix → 用 depth 和 key 做前缀比较nextByte = key[depth]child = findChild(node, nextByte)return search(child, key, depth + 1)
插入
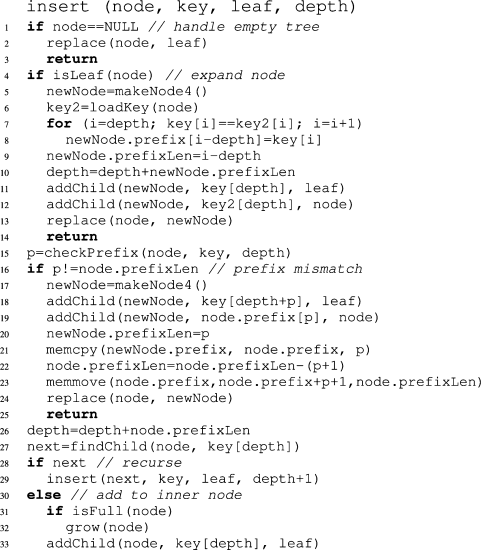
树的遍历是通过第 29 行的递归调用完成的,直到找到可以放置新叶子节点的位置。
- 常规情况:新叶子可以直接插入到已有的内部节点中,如果需要的话,先扩展该内部节点(第 31–33 行)。
- 延迟展开(lazy expansion)情况:如果在插入过程中遇到了一个现有的叶子节点,则用一个新的内部节点替换它,并将现有叶子和新叶子都挂在该内部节点下(第 5–13 行)。
- 压缩路径冲突情况:如果新叶子的 key 与当前节点的压缩路径(compressed path)不同,则需要在当前节点之上创建一个新的内部节点,并调整相应的压缩路径(第 17–24 行)。
由于篇幅限制,这里省略了一些辅助函数的实现:
replace:用另一个节点替换树中的某个节点。
addChild:向内部节点添加一个新的子节点。
checkPrefix:比较节点的压缩路径与 key,返回相同字节的数量。
grow:将节点替换为更大的节点类型(例如 Node4 → Node16)。
loadKey:从数据库中获取叶子节点的 key。
批量构建(Bulk loading):
当为一个已有的关系(relation)创建索引时,可以用如下递归算法加速构建过程:使用每个 key 的第一个字节,将键值对按基数(radix)划分为 256 个分区。创建一个合适类型的内部节点。在返回该内部节点之前,对每个分区递归地应用批量构建过程,使用每个 key 的下一个字节进行划分。
举例批量构建:
批量构建是为了 一次性高效建立整个 ART 树,而不是像普通插入那样一个 key 一个 key 地递归插入。
普通插入:每插入一个 key 都要从根走一遍路径,重复比较和分裂节点,速度慢。
批量构建:一次性把所有 key 按前缀分组,然后直接建出节点结构,省去了大量中间比较和节点分裂的开销。
核心思想:分治 + 基数分区(Radix Partition)
批量构建的算法是递归的,每一层按 当前字节(8 位) 的值把所有 key 分成 256 个组(因为一个字节 0~255)。比如有 10 个 key(这里假设 key 是字节数组):
"apple"
"apply"
"april"
"apt"
"bat"
"ball"
"banana"
"cat"
"dog"
"door"
第一步:按第 0 个字节(key[0])分组:
'a' 组:apple, apply, april, apt
'b' 组:bat, ball, banana
'c' 组:cat
'd' 组:dog, door
其他字节值组为空,这样就得到了 256 个分区,大部分是空的。
构建当前节点:根据非空分区的数量,创建一个合适的节点类型(Node4、Node16、Node48、Node256)。
如果只有 4 个非空分区 → Node4
如果 <= 16 个 → Node16
如果 <= 48 个 → Node48
否则 → Node256
节点的分支 key 就是当前字节值(比如 ‘a’,ASCII 97)。
递归构建子节点:对于每个非空分区,取该分区里所有 key,把“当前字节”当作已经处理过的部分(即 depth + 1),用这些 key 的下一个字节再次分成 256 个分区,重复步骤 3 构建子节点
递归结束条件:如果某个分区里只有一个 key,就直接创建一个叶子节点(leaf)。如果某个 key 的长度已经处理完(depth >= keyLen),也直接生成叶子。
空间消耗
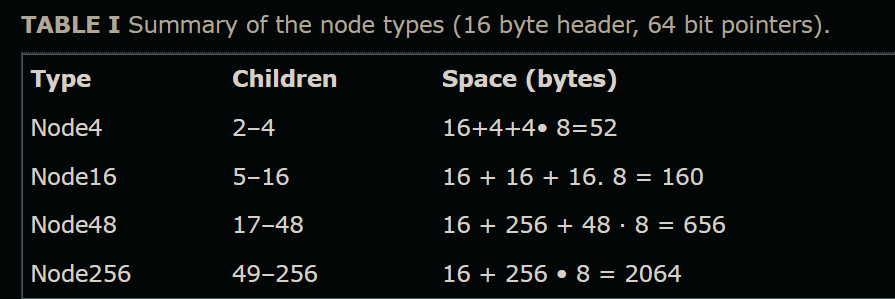
构造二进制可比较的键
在选择索引结构时,一个重要的方面是数据是否以有序的方式存储。索引结构的有序遍历有助于高效实现有序范围扫描、最小值/最大值查找、Top-N 查询等操作。默认情况下,只有基于比较的树(如B树、红黑树等)会以有序方式存储数据,这也是它们在数据库系统中广泛应用的原因。虽然有人提出使用保持顺序的哈希(order-preserving hashing)来让哈希表中的元素有序,但在实际系统中并不常见。原因在于,对于分布未知的数据,很难设计出既能均匀分布输入值、又能保持输入顺序的哈希函数。
在基数树(radix tree)中,键是按位(bitwise)字典序(lexicographical)排序的。对于某些数据类型,比如ASCII编码的字符串,这种排序方式正好符合我们的预期。但对于大多数数据类型并非如此。例如,负的二进制补码有符号整数在字典序上会排在正整数后面(即负数比正数大)。不过,我们可以通过对键进行转换,得到我们想要的顺序。我们把这种转换后的值称为二进制可比较的键(binary-comparable keys)。如果只使用二进制可比较的键作为基数树的键,数据就会以有序方式存储,所有依赖于有序性的操作都能得到支持。需要注意的是,不需要对前面介绍的算法做任何修改,只需在存储或查找键之前,把每个键转换为二进制可比较的键即可。
二进制可比较的键还有其他用途。正如这个概念可以让我们用基数树替代基于比较的树一样,它也可以让我们用基数排序(radix sort)替代像快速排序(quicksort)或归并排序(mergesort)这样的比较排序算法,而基数排序在渐进意义上可能更优。
定义
一个转换函数
t:D→{0,1,…,255}kt: D \to \{0,1,\dots,255\}^k t:D→{0,1,…,255}k
如果满足以下等价关系,就称它能将定义域 DDD 中的值转换为长度为 kkk 的二进制可比较键(binary-comparable keys):
x<y⟺memcmpk(t(x),t(y))<0x < y \iff \text{memcmp}_k(t(x), t(y)) < 0 x<y⟺memcmpk(t(x),t(y))<0
x>y⟺memcmpk(t(x),t(y))>0x > y \iff \text{memcmp}_k(t(x), t(y)) > 0 x>y⟺memcmpk(t(x),t(y))>0
x=y⟺memcmpk(t(x),t(y))=0x = y \iff \text{memcmp}_k(t(x), t(y)) = 0 x=y⟺memcmpk(t(x),t(y))=0
其中,运算符 <, >, = 是指输入类型(原始数据类型)上的通常比较运算;
memcmpk\text{memcmp}_kmemcmpk 表示逐字节(component-wise)比较两个长度为 kkk 的向量:
- 如果所有比较位置的值都相等,则返回 0;
- 如果第一个不相等的位置上,第一个向量的值小于第二个向量对应位置的值,则返回 负值;
- 否则(大于)返回 正值。
对于有限域(finite domain),任何严格全序(strictly totally ordered)的数据域,都可以转换成二进制可比较键:
定义域大小为 nnn 的每个值,可以映射成一个长度为 ⌈log2n⌉\lceil \log_2 n \rceil⌈log2n⌉ 位(bits)的二进制串,这个二进制串存储的是零扩展后的秩值(rank)减一。
解释
-
t 函数的作用
- 这是一个“排序保持”的映射:它把原数据(比如整数、浮点数、日期等)转换成固定长度的二进制序列(长度为 k 字节)。
- 转换后的序列在按字典序(memcmp)比较时,与原数据的大小关系完全一致。
-
memcmp 的意义
-
memcmp是 C 语言里的一个内存比较函数,这里数学化了它的定义:- 按字节逐个比较,直到遇到第一个不同的字节;
- 小于返回负值,大于返回正值,完全相等返回 0。
-
这样比较二进制串时,实际上是在做字典序比较(lexicographical compare)。
-
-
有限域如何实现转换
- 如果数据域是有限的,并且有严格的全序关系(即任意两个值都能比较出大小),那么一定可以为每个值分配一个秩值(rank),秩值从 0 到 n−1n-1n−1。
- 再把这个秩值转成二进制,长度取刚好能表示 n−1n-1n−1 所需的比特数:⌈log2n⌉\lceil \log_2 n \rceil⌈log2n⌉ 位。
- 如果位数不足 k 字节,前面用 0 填充(零扩展,zero-extend)。
- 这样得到的二进制串在字节比较时顺序与原数据顺序一致。
B. Transformations
a) 无符号整数(Unsigned Integers)
无符号整数的二进制表示本身就符合期望的顺序。
但在存储到内存时必须考虑机器的字节序(endianness):
- 在小端(little-endian)机器上,最低有效字节排在内存前面,所以需要交换字节顺序,确保最终的内存布局是从最高有效字节到最低有效字节,以保持比较结果正确。
b) 有符号整数(Signed Integers)
二补码(two’s complement)表示的有符号整数需要调整顺序,因为负数在二进制字典序中会排在正数后面。
解决办法:
-
对于 b 位整数 xxx,翻转符号位(sign bit),即执行:
x′=x⊕2b−1x' = x \oplus 2^{b-1} x′=x⊕2b−1
-
翻转后再按无符号整数的方式存储。这样,负数会正确排在正数之前。(反转是正负数都反转)
c) IEEE 754 浮点数(Floating Point Numbers)
浮点数的转换稍复杂,但原理简单。
- 首先对数值分类:正/负,正规化数(normalized)、非正规化数(denormalized)、NaN、∞、0。
- 由于这 10 种类别互不重叠,可以为它们分配一个新的秩(rank),再按无符号整数方式存储。
- 一个关键的转换过程需要:3 个 if 判断、1 次整数乘法、2 次加法。
(如果我们有一个数据域 D,并且里面的值有严格的大小关系,那么我们可以给每个值分配一个整数编号(从 0 开始),这个编号就是 rank。)
d) 字符串(Character Strings)
Unicode 字符串的比较规则由 UCA(Unicode Collation Algorithm) 定义,规则非常复杂。
- 有开源库实现了该算法,并提供将 Unicode 字符串转换为二进制可比较键的函数。
- 一般来说,每个字符串都必须以一个不会出现在任何字符串中其他位置的值作为结束符(比如
0x00或特殊符号°),以避免一个键是另一个键的前缀。
(普通的ASCII是逐字符比较,在 Unicode 字符串 有复杂情况,比如:不同的组合字符可能视觉上是同一个字母(例如 é 可以是单个字符,也可以是 ‘e’ + ’ ́’ 两个字符组合)。有的比较规则会忽略大小写、重音符号等(locale-aware collation)。不同语言对同样的 Unicode 字符排序规则不同。因此 UCA(Unicode Collation Algorithm) 不只是简单的字符编码比较,而是为每个字符分配一个比较权重(collation weight),这个权重本质上就是一个 rank。比较时不是直接用原始字符编码,而是用 rank 序列进行比较。)
e) 空值(Null)
为了让 Null 值可进行二进制比较,需要给它分配一个特定的秩(rank)。
-
对于大多数数据类型,其值域已被所有可能值占满,因此无法直接插入 Null。
-
解决办法 1:将所有键的长度增加 1 字节,为 Null 预留空间(例如 4 字节整数变为 5 字节)。
-
解决办法 2(更高效):只为部分值扩展长度。
- 例如,如果 Null 应小于所有 4 字节整数,可将 Null 映射为字节序列
0,0,0,0,0,原本最小值(比如0,0,0,0)映射为0,0,0,0,1,其余值保持原有的 4 字节表示。
- 例如,如果 Null 应小于所有 4 字节整数,可将 Null 映射为字节序列
f) 复合键(Compound Keys)
对于由多个属性组成的键,可以分别转换每个属性,然后将结果按顺序拼接即可。
无论原始数据是 整数 / 浮点数 / 字符串 / 日期 / Null / 复合键,都会先经过“类型内的转换”(前面提到的 unsigned int、signed int、float、string 等转换规则),然后再加上 类型间的排序规则,把它们映射到一个统一的字节序列。
比如:
Null < Boolean < Integer < Float < String < DateTime < Blob
比较
在本节中,我们对 ART(Adaptive Radix Tree) 进行实验评估,并将其性能与其他内存数据结构进行比较,这些数据结构包括基于比较的树结构、哈希结构以及基数树结构。评估分为两个部分:
- 微基准测试(micro benchmarks):作为独立程序运行,涵盖所有被测试的数据结构;
- 数据库系统集成测试:将部分数据结构集成到内存数据库系统 HyPer 中,执行更贴近真实环境的标准 OLTP 基准测试 TPC-C。
对比选手: - CSB±Tree:为内存优化的 B+ 树(Cache-Sensitive B±tree)
- k-ary Search Tree(kary):针对现代 x86 CPU 优化的只读搜索树 FAST(Fast Architecture Sensitive -Tree)
- 同样针对现代 x86 架构优化的只读搜索树 GPT(Generalized Prefix Tree):基数树
- RB:教科书实现的红黑树 HT:使用 MurmurHash64A(适配 64 位平台)的链式哈希表
