[ LeetCode-----盛最多的水]

1.题目链接

LeetCode盛最多的水

2.题目描述

 

 

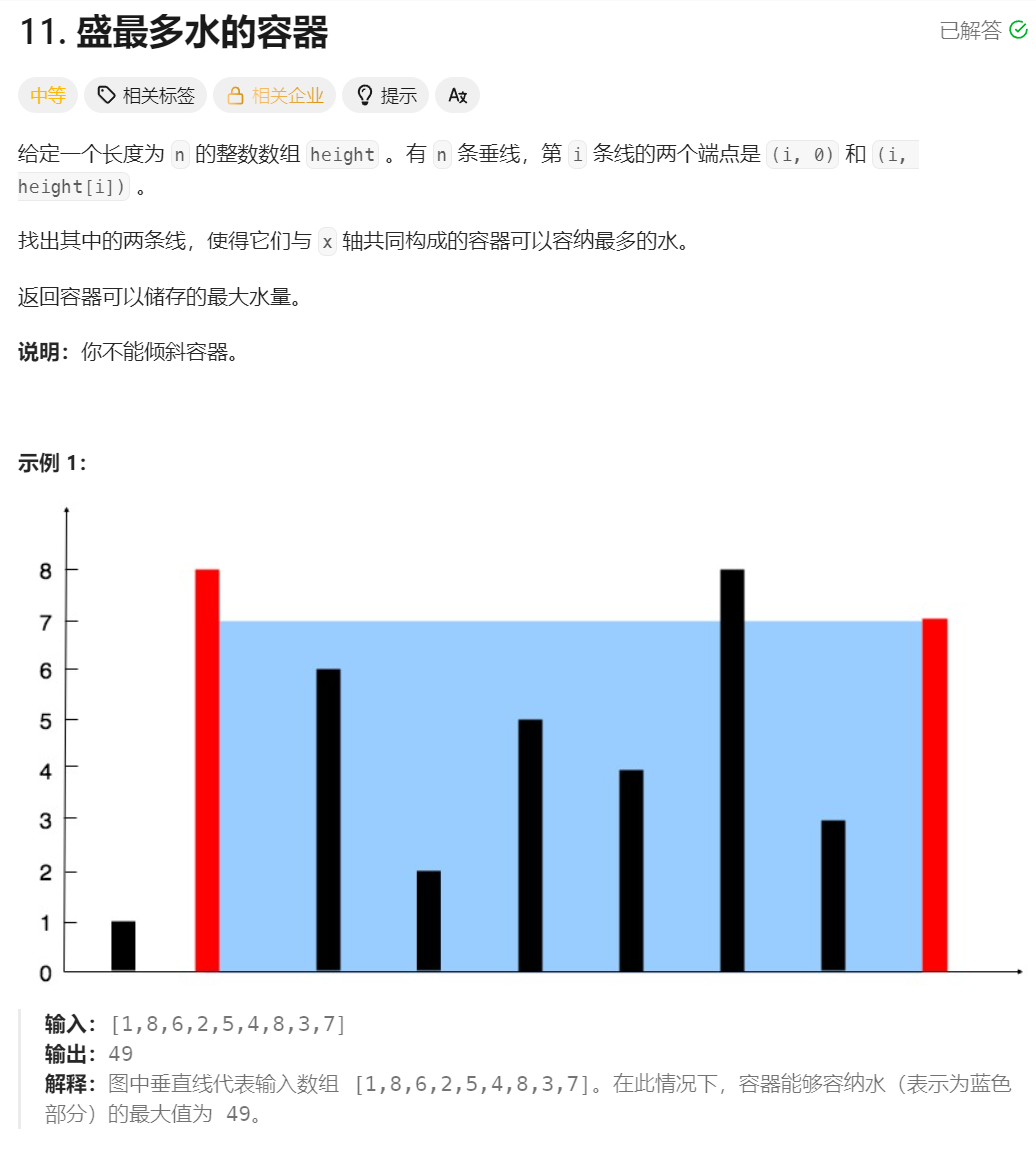
3.题目解析 

问题本质分析

"盛最多水的容器" 问题可以抽象为：在坐标轴上有 n 条垂直线段，第 i 条线段的两个端点分别是 (i, 0) 和 (i, height [i])。找到两条线段，使得它们与 x 轴共同构成的容器能够容纳最多的水。

容器的容量计算公式是：面积 = 宽度 × 高度，其中：

• 宽度 = 两条线段的横坐标之差
• 高度 = 两条线段中较短那条的长度（因为水会从较短的一边溢出）

 

算法核心思路

采用双指针从两端向中间移动，通过贪心策略每次选择可能获得更大面积的移动方向：

1. 初始状态：左指针在最左端 (left=0)，右指针在最右端 (right=height.size ()-1)
2. 计算当前面积：以当前双指针为边界计算容器面积
3. 更新最大面积：如果当前面积大于历史最大值，则更新
4. 移动指针：
   • 若左指针指向的线段更短，移动左指针 (left++)
   • 否则，移动右指针 (right--)
5. 终止条件：左右指针相遇 (left>= right)

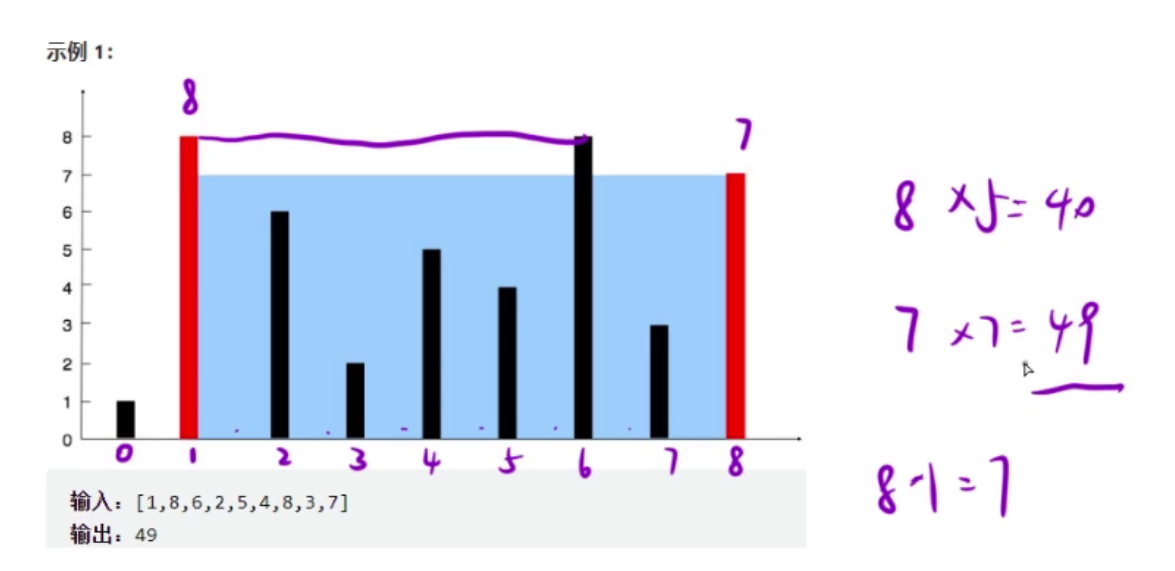
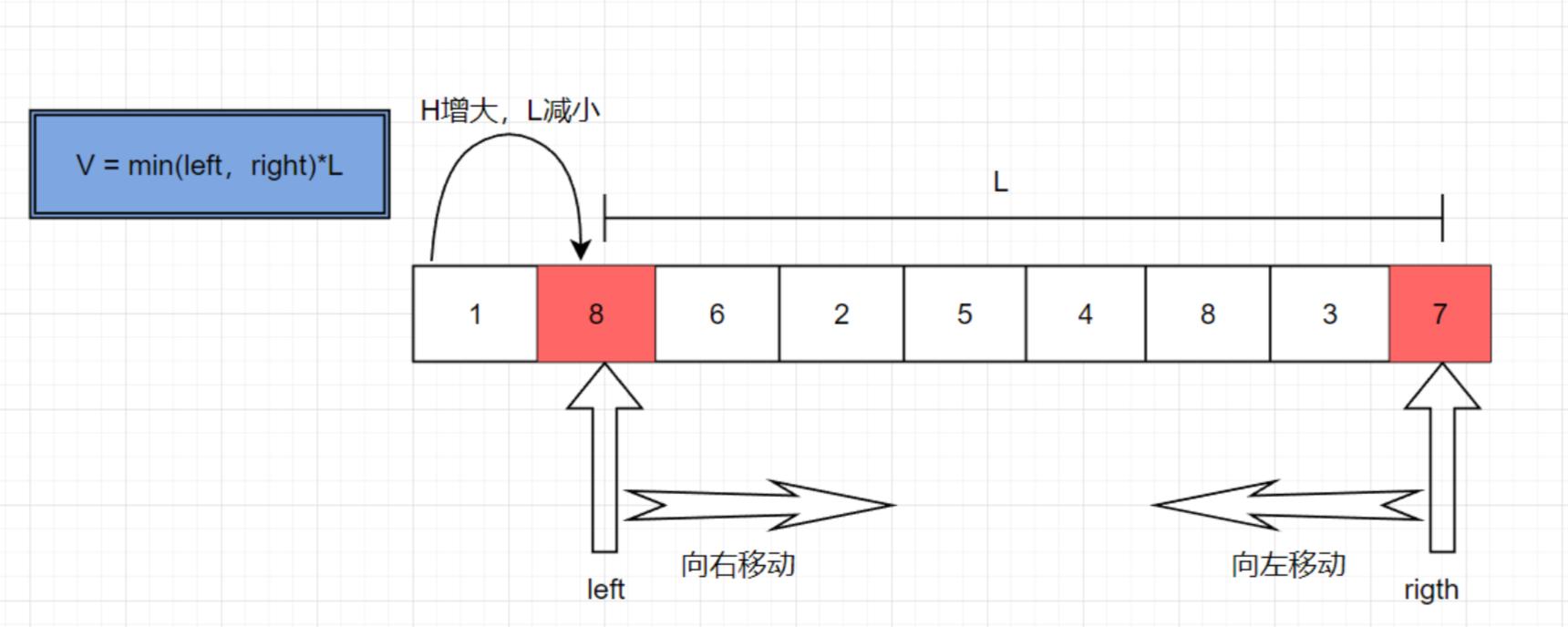
 下面我们画图理解：

1.定义两个指针分别从左右两端开始,计算当前的V

 

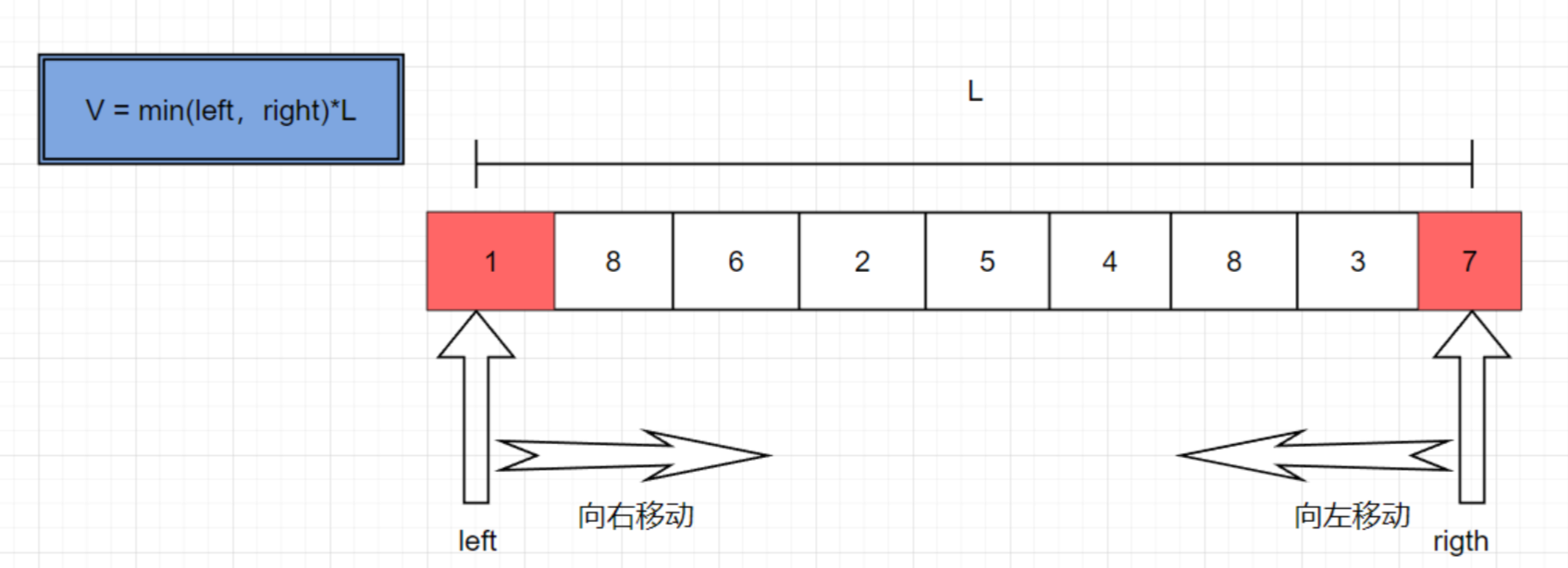
2.接着开始移动指针 

如果移动right,L会减小,H也会减小,则V一定减小,所以没必要这么做. 

 

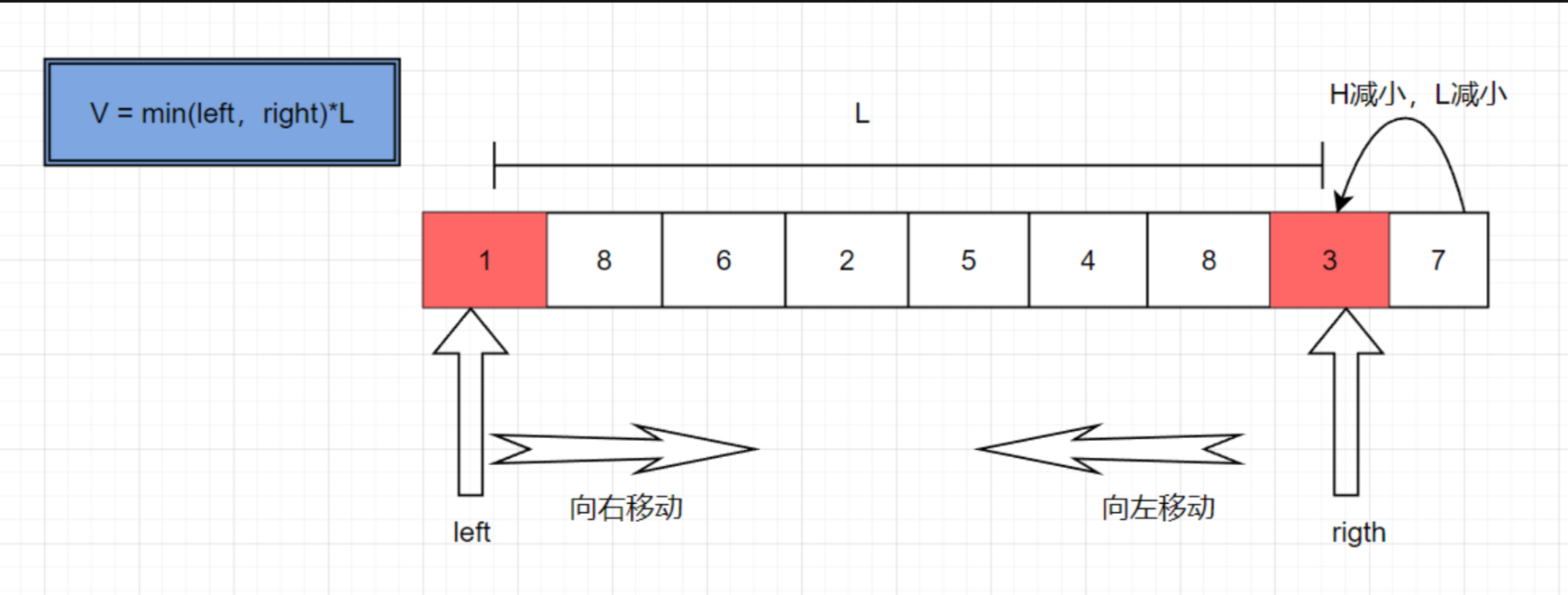
如果移动left,L会增大,H会减小,但V有可能增大 

 

 

为什么这样移动指针是正确的？

这是理解算法的关键。假设我们有两个指针 left 和 right，且 height [left] < height [right]：

• 如果我们移动右指针，新的宽度一定减小（因为 right-left 变小）
• 新的高度取决于新的 right' 和原 left 中的较小值，由于原 left 是较短的，新高度不会超过原高度
• 因此，移动右指针只会得到更小的面积，不可能得到更大的面积

反之，如果 height [right] 更短，移动左指针也会导致面积减小。因此，只有移动较短的指针才有可能获得更大的面积，这是一种贪心策略的体现。

 

这种双指针解法的优势在于：

• 时间效率高：只需遍历一次数组，O (n) 时间复杂度
• 空间效率高：只使用常数级额外空间，O (1) 空间复杂度
• 思路简洁：通过贪心策略每次做出局部最优选择，最终得到全局最优解

这个算法充分体现了贪心算法的思想 —— 通过每一步的局部最优选择，最终达到全局最优。

 

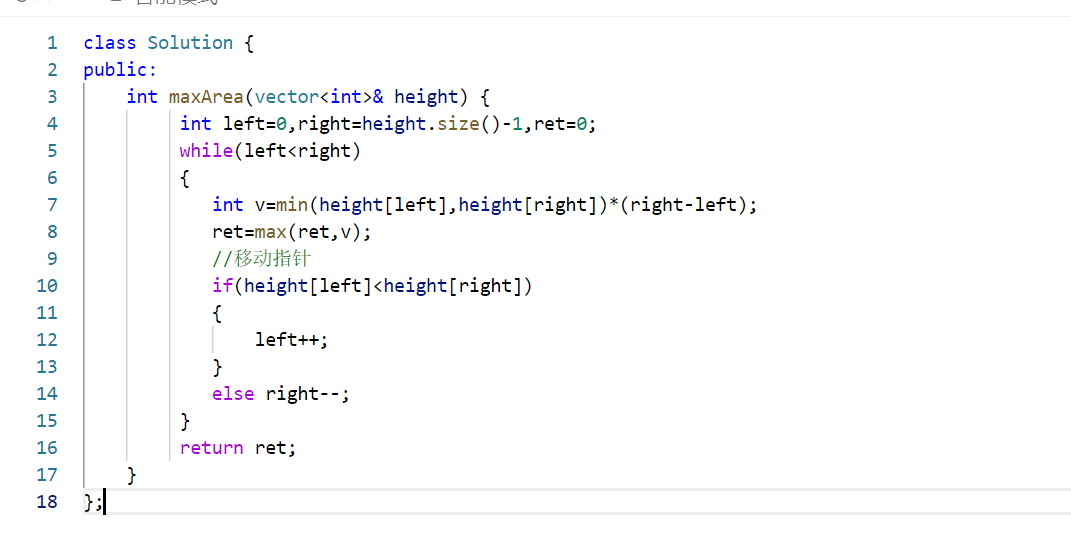
完整代码： 

 

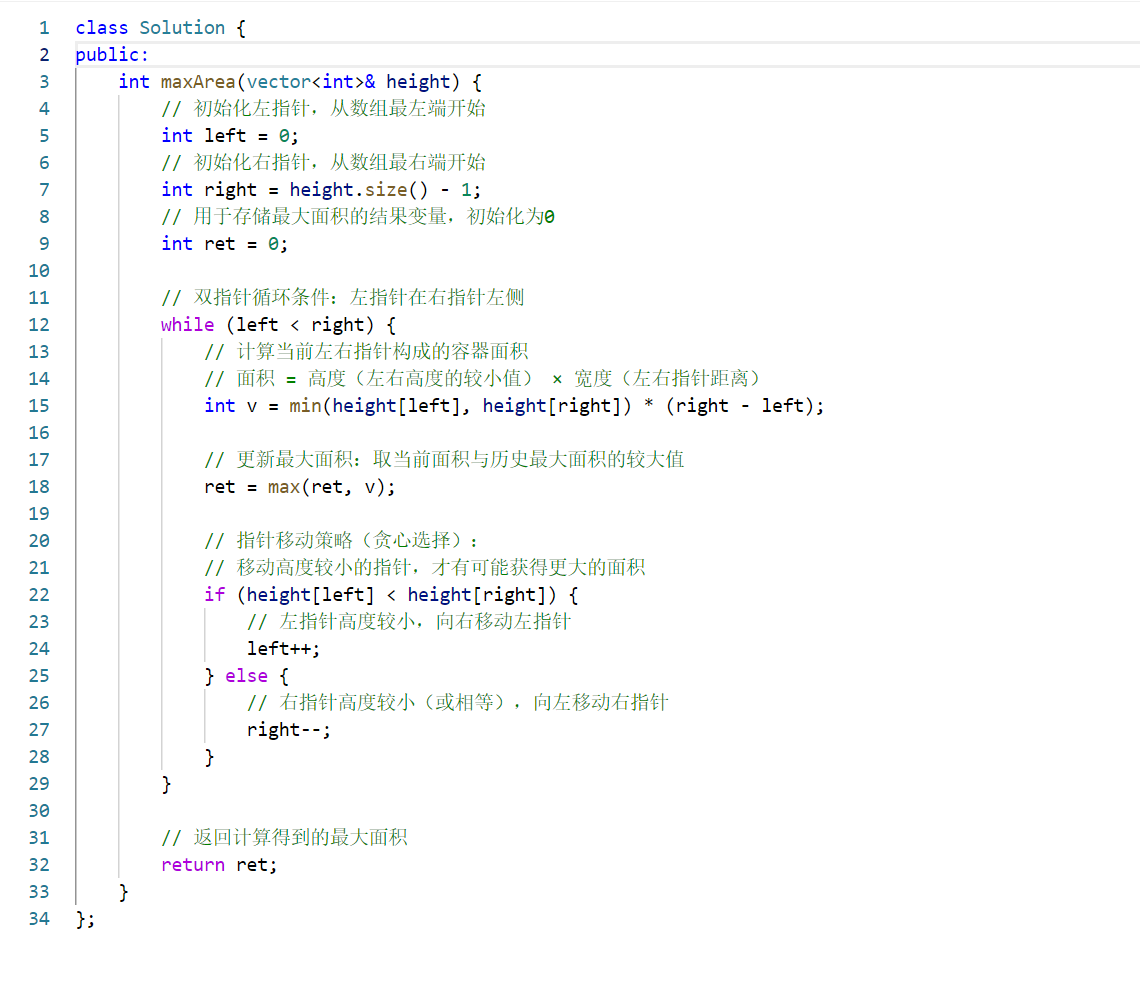
代码注释： 

 

复杂度分析 

该双指针解法在时间和空间上都达到了最优：

• 时间复杂度：O (n)（线性时间，遍历一次数组）
• 空间复杂度：O (1)（常数空间，不依赖输入规模）

这也是该算法被认为是「盛最多水的容器」问题最优解的核心原因 —— 在保证正确性的前提下，实现了极高的效率。