排序算法大全:从插入到快速排序
排序算法大全:从插入到快速排序
- 1. 插入排序
- 2. 希尔排序
- 3. 冒泡排序
- 4. 选择排序
- 5. 堆排序
- 6. 快速排序
- 6.1 递归算法
- 6.2 非递归算法
- 7. 归并排序
- 7.1 递归算法
- 7.2 非递归算法
- 8. 计数排序
- 9. 对比
在我们日常生活中,排序的应用无处不在,几乎涉及到生活的方方面面。从简单的日常事务到复杂的系统管理,排序都发挥着重要作用。
-
在图书馆里,图书管理员会按照图书编号的字母和数字顺序将书籍排列在书架上。
-
手机通讯录默认按照联系人姓名的拼音首字母顺序排列,这种排序方式让我们能够快速找到想要联系的人。
-
学校公布考试成绩时,通常会按照分数从高到低排序,这样能直观地看到学生的成绩分布情况。
这些例子都说明了排序在提高生活效率、优化用户体验方面的重要作用。合理的排序方式能让信息更易获取,决策更有效率,是现代生活中不可或缺的组织工具。
那么本章将会介绍排序相关内容。
1. 插入排序
插入排序是一种简单直观的基于比较的排序算法,适用于小规模数据或部分有序的数据集。它的核心思想是将数组分为“已排序”和“未排序”两部分,逐个将未排序元素插入到已排序部分的正确位置。
如图所示:

void InsertSort(int* a, int n) { //a:数组 n:数组长度for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0) {if (tmp < a[end]) { //<:升序 >:降序a[end + 1] = a[end];end--;}else {break;}}a[end + 1] = tmp;}
}
2. 希尔排序
希尔排序(Shell Sort)是插入排序的改进版本,由 Donald Shell 于 1959 年提出。它通过分组插入排序的方式,使得数据能够更快地接近有序,从而减少比较和交换的次数,提高排序效率。
void ShellSort(int* a, int n) {int gap = n;while (gap > 1) {gap = gap / 3 + 1; //也可改成gap = gap / 2;(保证gap最后为 1 即可)////一组 :将当前数据与当前数据间隔为gap的所有数据进行排序//for (int j = 0; j < gap; j++) {// for (int i = j; i < n - gap; i += gap) {// int end = i;// int tmp = a[end + gap];// while (end >= 0) {// if (tmp > a[end]) {// a[end + gap] = a[end];// end - gap;// }// else {// break;// }// }// a[end + gap] = tmp;// }//}//多组 :将当前数据与当前数据间隔为gap的下一个数据进行排序for (int i = 0; i < n - gap; i++) {int end = i;int tmp = a[end + gap];while (end >= 0) {if (tmp < a[end]) {a[end + gap] = a[end];end -= gap;}else {break;}}a[end + gap] = tmp;}}
}
如图所示(一组):
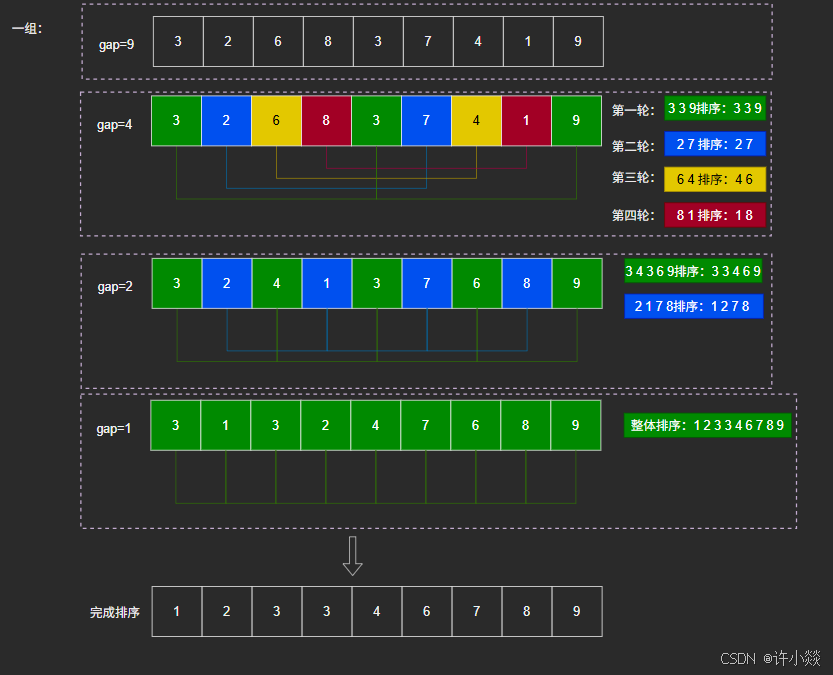
如图所示(多组):
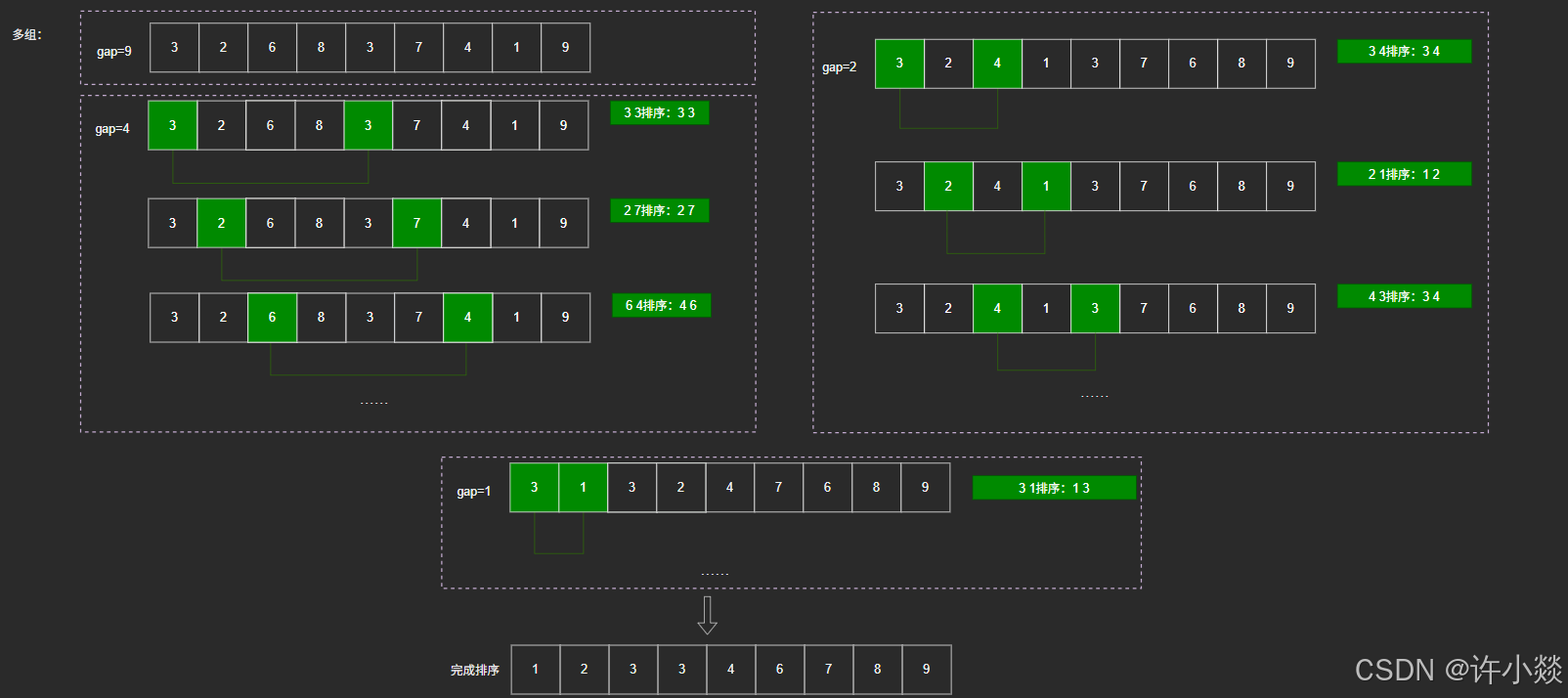
3. 冒泡排序
冒泡排序是一种简单的基于比较的排序算法,它通过反复交换相邻的逆序元素,使得较大的元素逐渐“浮”到数组的末端。尽管效率不高,但由于其实现简单,常用于教学和小规模数据排序。
如图所示:

void BubbleSort(int* a, int n) {for (int i = 0; i < n; i++) {bool flag = true;for (int j = 0; j < n - i - 1; j++) {if (a[j] > a[j + 1]) {int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;flag = false;}}if (flag) //若没发生交换,则表明有序,直接跳出break;}
}
4. 选择排序
选择排序是一种简单直观的基于比较的排序算法,其核心思想是每次从未排序部分选出最小(或最大)元素,放到已排序部分的末尾(也可放在开头)。虽然效率不高,但由于实现简单,适用于小规模数据或辅助教学。
如图所示:

void Swap(int* x, int* y) { //交换int tmp = *x;*x = *y;*y = tmp;
}//普通选择排序
void Normal_SelectSort(int* a, int n) {for (int i = 0; i < n - 1; i++) {int m = i;for (int j = i + 1; j < n; j++) {if (a[j] < a[m]) { //<:升序 >:降序m = j;}}Swap(&a[i], &a[m]); //交换}
}// 选择排序(两端同时进行)
void SelectSort(int* a, int n) {int begin = 0;int end = n - 1;while (begin < end) {int max = begin;int min = begin;for (int i = begin + 1; i <= end; i++) {if (a[i] > a[max]) {max = i;}else if (a[i] < a[min]) {min = i;}}Swap(&a[min], &a[begin]);if (max == begin)max = min;Swap(&a[max], &a[end]);begin++;end--;}
}
5. 堆排序
堆排序是一种基于二叉堆数据结构的比较排序算法。它是一种选择排序的改进版本,具有O(n log n)的时间复杂度。
可参考:堆排序与Top K问题精解
6. 快速排序
快速排序是一种高效的、基于分治思想的排序算法,由Tony Hoare于1959年提出。它是实际应用中最快的已知排序算法之一,多使用递归实现,平均时间复杂度为O(n log n)。
6.1 递归算法
// hoare版本
int PartSort1(int* a, int begin, int end) {int mid = GetMid(a, begin, end);Swap(&a[begin], &a[mid]);int left = begin;int right = end;int key = begin;while (left < right) {//右边找小while (left < right && a[right] >= a[key]) {right--;}//左边找大while (left < right && a[left] <= a[key]) {left++;}Swap(&a[left], &a[right]); //交换}Swap(&a[key], &a[left]); //交换return left;
}
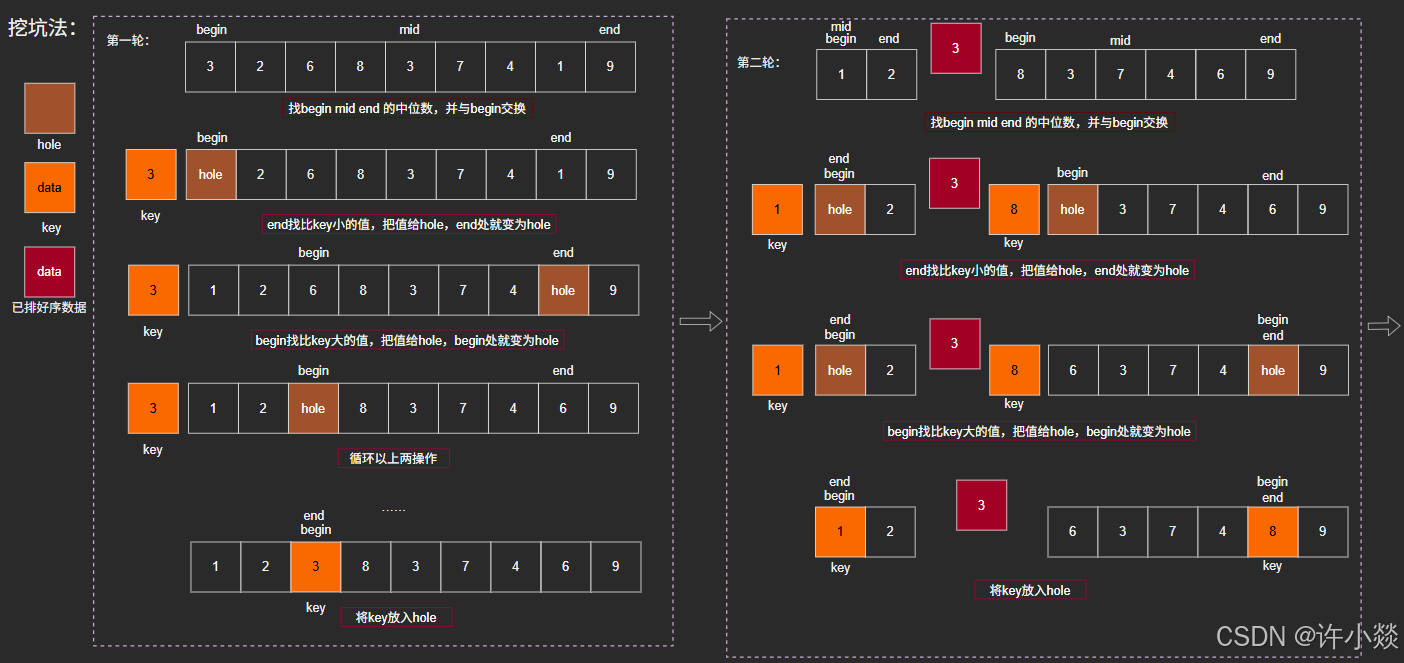
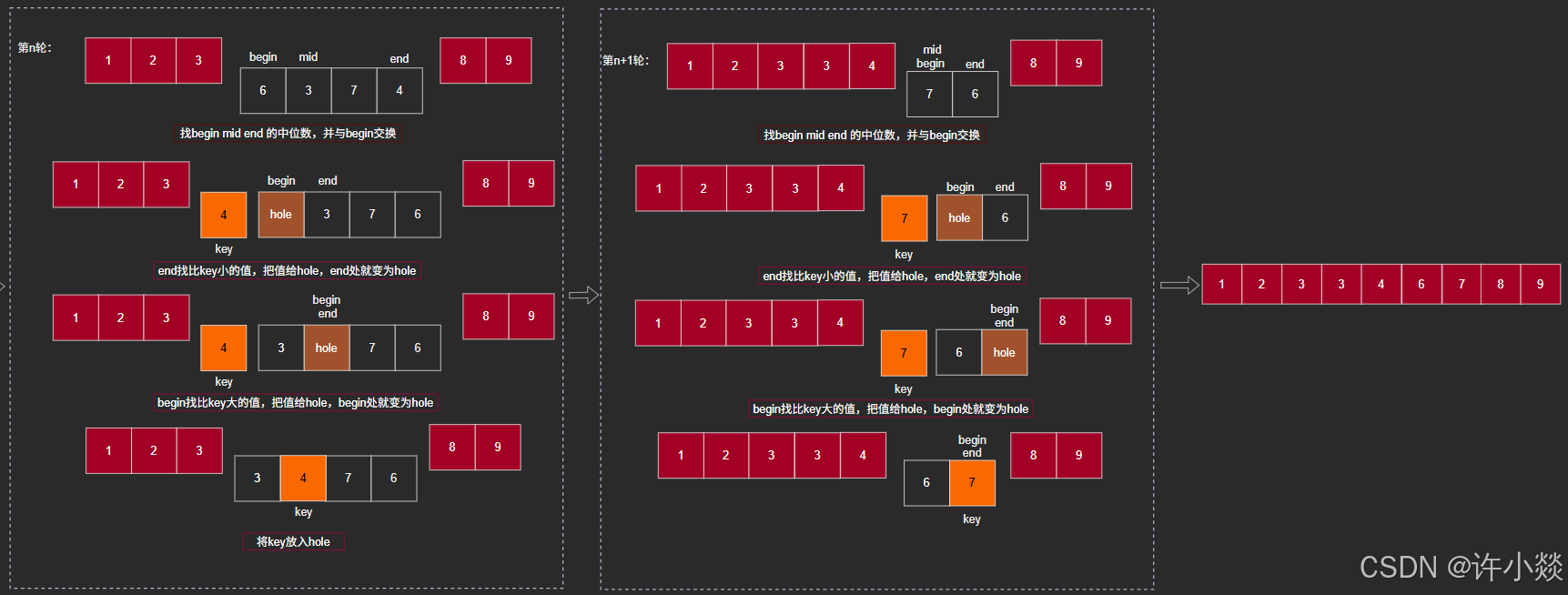
// 挖坑法
int PartSort2(int* a, int begin, int end) {int mid = GetMid(a, begin, end);Swap(&a[begin], &a[mid]);int key = a[begin];int hole = begin;while (begin < end) {//右边找小while (begin < end && a[end] >= key) {end--;}a[hole] = a[end];hole = end;//左边找大while (begin < end && a[begin] <= key) {begin++;}a[hole] = a[begin];hole = begin;}a[hole] = key; //最后要把“坑”填上return hole;
}
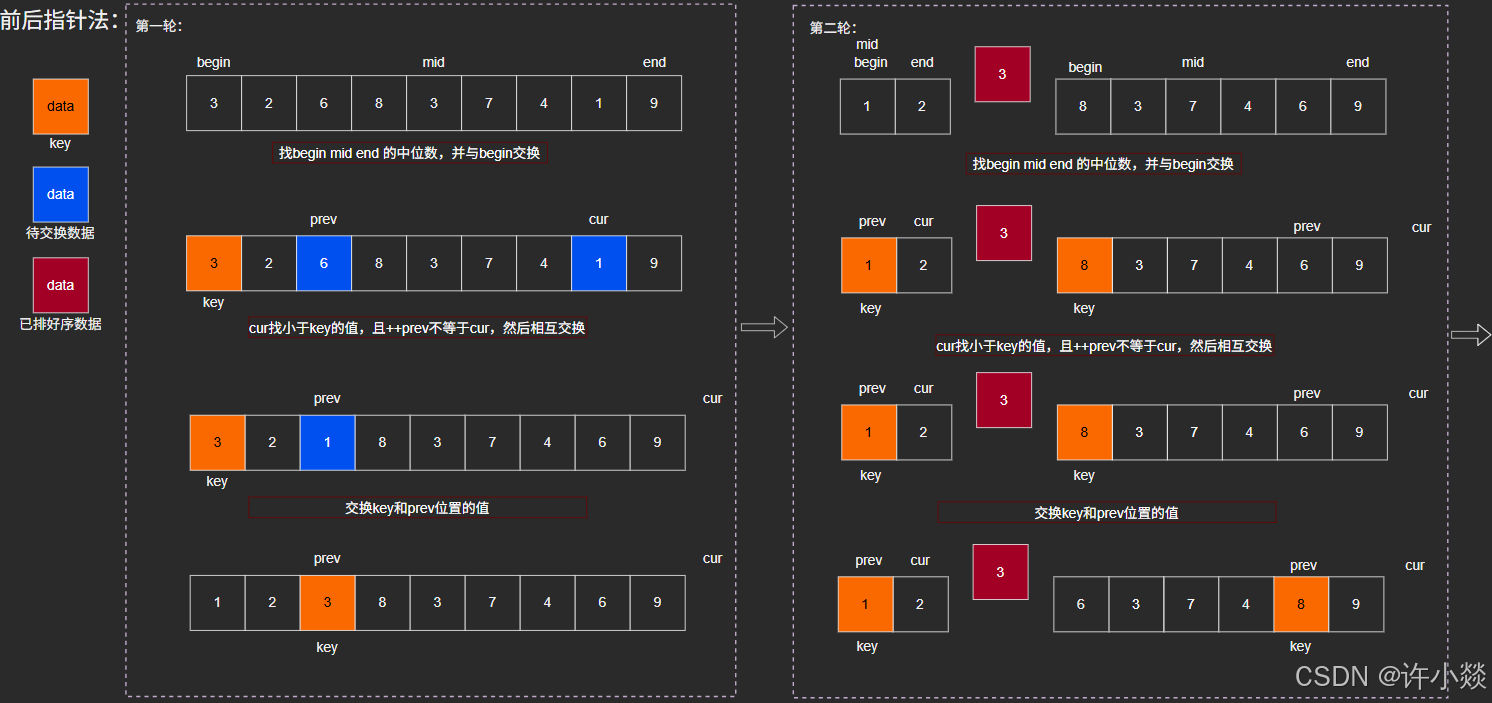
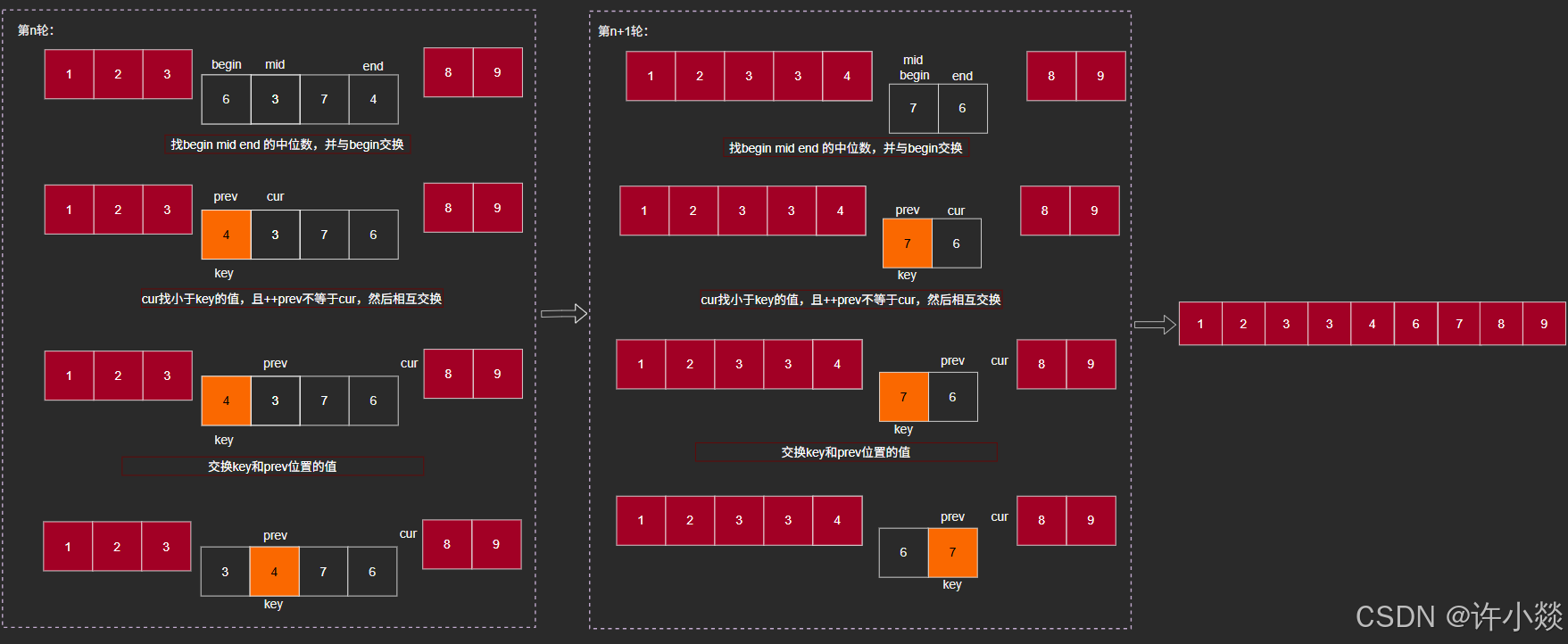
// 前后指针法
int PartSort3(int* a, int begin, int end) {int mid = GetMid(a, begin, end);Swap(&a[begin], &a[mid]);int key = begin;int prev = begin;int cur = prev + 1;while (cur <= end) {if (a[cur] < a[key] && ++prev != cur) { //这一步是关键Swap(&a[prev], &a[cur]);}cur++;}Swap(&a[prev], &a[key]); //交换key = prev;return prev;
}
//时间复杂度O(N*logN)
void QuickSort(int* a, int begin, int end) {if (begin >= end) {return;}//数据长度小于10 直接使用插入排序(用于处理大量数据)if (end - begin + 1 <= 10) {InsertSort(a + begin, end - begin + 1); //小区间的优化}else {//int key = PartSort1(a, begin, end);//QuickSort(a, begin, key - 1);//QuickSort(a, key + 1, end);//int key = PartSort2(a, begin, end);//QuickSort(a, begin, key - 1);//QuickSort(a, key + 1, end);int key = PartSort3(a, begin, end);QuickSort(a, begin, key - 1);QuickSort(a, key + 1, end);}
}
hoare版:
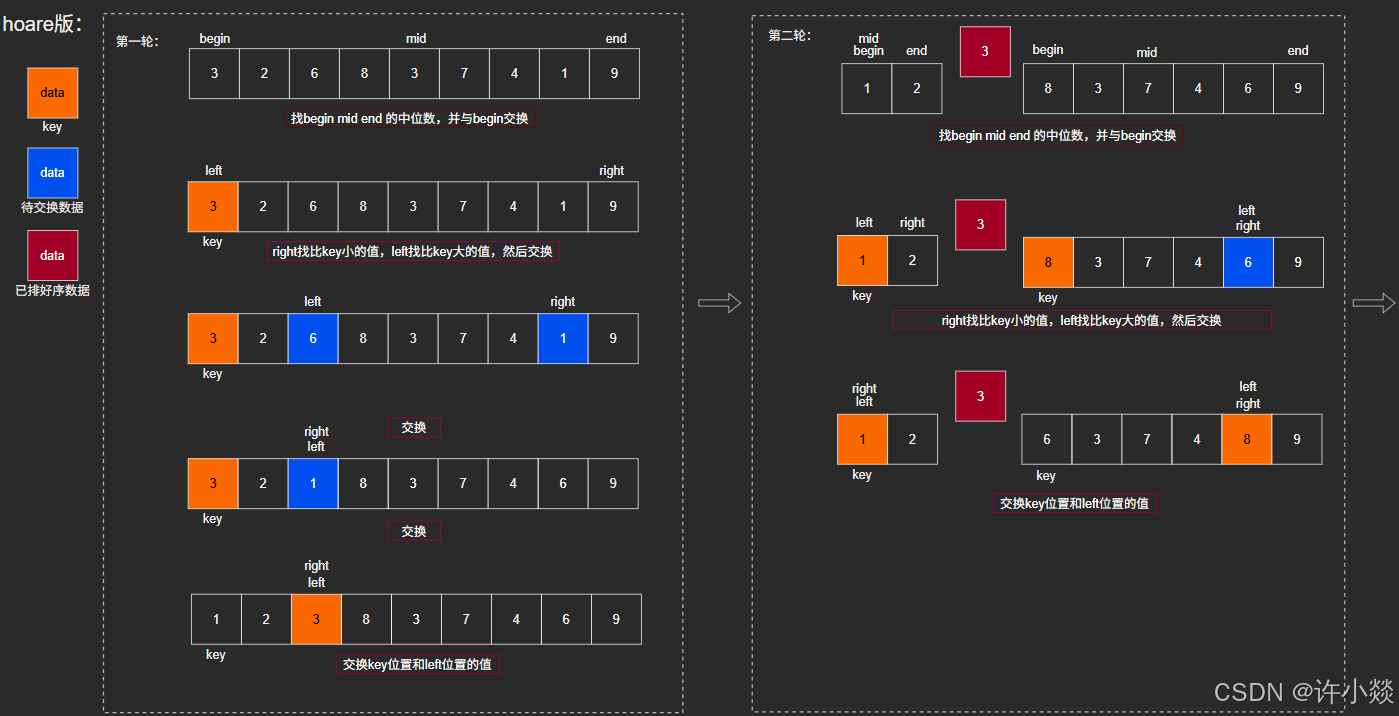
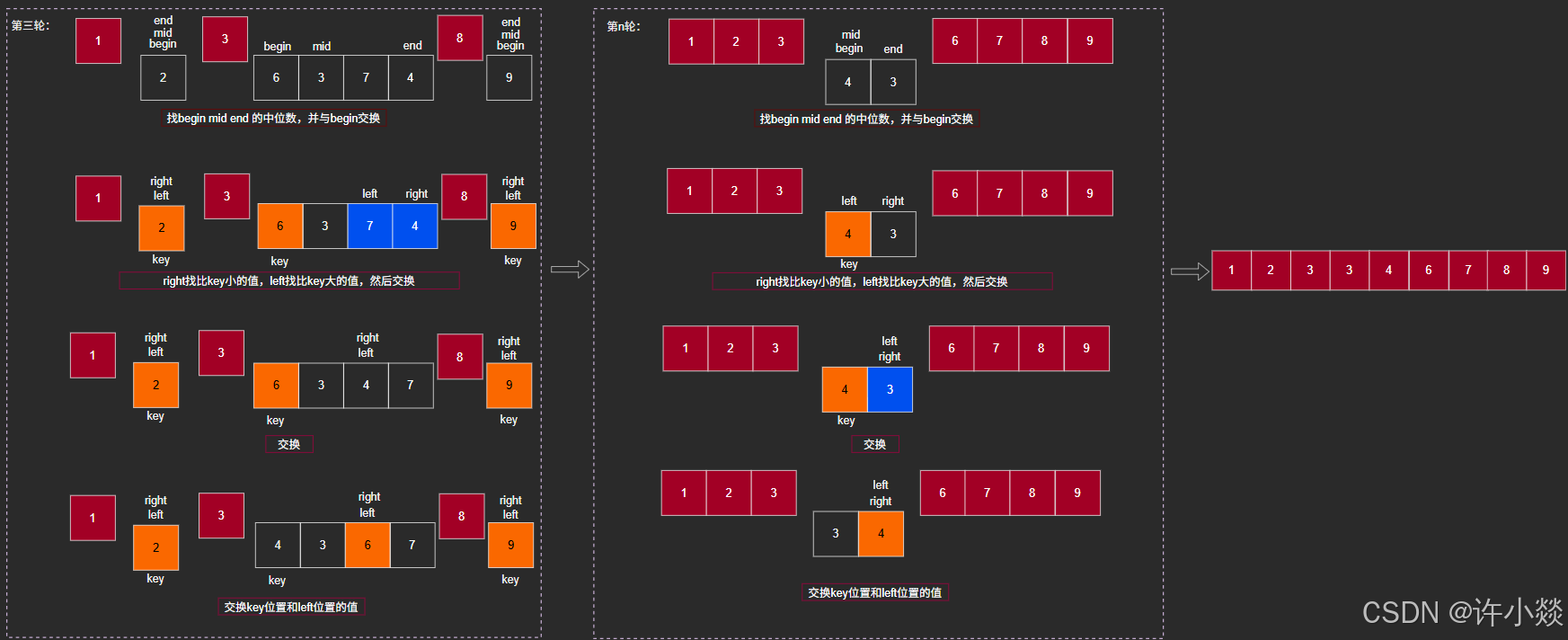
挖坑法:
前后指针法:
6.2 非递归算法
非递归算法通常借助栈结构实现,利用其先进后出的特性来模拟递归过程,从而完成快速排序的非递归实现。
typedef int STDataType;
typedef struct Stack
{STDataType* a;int top; // 栈顶int capacity; // 容量
}Stack;//栈的初始化
void StackInit(Stack* ps) {assert(ps);ps->a = NULL;ps->top = -1;ps->capacity = 0;
}// 入栈
void StackPush(Stack* ps, STDataType data) {assert(ps);if (ps->top + 1 == ps->capacity) {int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);if (tmp == NULL) {perror("realloc fail!");return;}ps->a = tmp;ps->capacity = newcapacity;}++ps->top;ps->a[ps->top] = data;
}// 出栈
void StackPop(Stack* ps) {assert(ps);assert(ps->top >= 0);ps->top--;
}// 获取栈顶元素
STDataType StackTop(Stack* ps) {assert(ps);assert(ps->top >= 0);return ps->a[ps->top];
}// 检测栈是否为空,如果为空返回非零结果,如果不为空返回0
bool StackEmpty(Stack* ps) {assert(ps);return ps->top == -1;
}
// 销毁栈
void StackDestroy(Stack* ps) {assert(ps);free(ps->a);ps->a = NULL;ps->top = -1;ps->capacity = 0;
}// 快速排序 非递归实现
void QuickSortNonR(int* a, int begin, int end) {Stack s;StackInit(&s); //初始化栈StackPush(&s, end); //end入栈StackPush(&s, begin); //begin入栈while (!StackEmpty(&s)) {int left = StackTop(&s); //取栈顶元素StackPop(&s); //出栈int right = StackTop(&s); //取栈顶元素StackPop(&s); //出栈int key = PartSort3(a, left, right); //通过前后指针法找到keyif (left < key - 1) {StackPush(&s, key - 1); //入栈顺序与上面保持一致StackPush(&s, left);}if (key + 1 < right) {StackPush(&s, right);StackPush(&s, key + 1);}}StackDestroy(&s);
}
注意:栈存储的是数组下标而非直接操作数据,通过循环方式实现递归逻辑。
7. 归并排序
归并排序(Merge Sort)是一种基于分治法(Divide and Conquer)的高效排序算法,其核心思想是:
-
分解(Divide):将数组递归地分成两半,直到每个子数组只含一个元素(自然有序)。
-
合并(Merge):将两个有序子数组合并成一个更大的有序数组。
如图所示:

7.1 递归算法
void _MergeSort(int* a, int begin, int end, int* tmp) { //tmp是临时数组if (begin >= end) { //递归终止条件return;}int mid = (begin + end) / 2; //找中//分割成两组//[begin,mid][mid+1,end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);int begin1 = begin, end1 = mid; //左区间int begin2 = mid + 1, end2 = end; //右区间int i = begin;while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) { //升序tmp[i++] = a[begin1++];}else {tmp[i++] = a[begin2++];}}while (begin1 <= end1) {tmp[i++] = a[begin1++]; //左区间剩余的数据}while (begin2 <= end2) {tmp[i++] = a[begin2++]; //右区间剩余的数据}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));//复制将tmp中的元素复制到原数组中(begin不要掉了)
}void MergeSort(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n); //开辟一个新数组存放排序的数据if (tmp == NULL) {perror("malloc fail!");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
7.2 非递归算法
归并排序的非递归实现采用自底向上的策略。算法首先将数组划分为最小单元(两个元素)进行排序,然后逐步扩大区间范围,通过不断合并相邻有序子数组来完成整体排序。具体步骤为:初始阶段将数组划分为两两一组进行排序;随后将相邻有序子数组合并为更大的有序区间(四个元素一组);重复这一过程直至整个数组合并完成,最终得到完全有序的数组。
void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL) {perror("malloc fail!");return;}int gap = 1; //当前归并的子数组的长度while (gap < n) {printf("gap->%2d:", gap);for (int i = 0; i < n; i += 2 * gap) {int begin1 = i, end1 = i + gap - 1; //左子区间int begin2 = i + gap, end2 = i + 2 * gap - 1; //右子区间if (end1 >= n || begin2 >= n) {break;}if (end2 >= n) {end2 = n - 1; //数组个数为奇数的情况}printf("[%2d,%2d][%2d,%2d]", begin1, end1, begin2, end2);int j = begin1;while (begin1 <= end1 && begin2 <= end2) {if (a[begin1] < a[begin2]) {tmp[j++] = a[begin1++];}else {tmp[j++] = a[begin2++];}}while (begin1 <= end1) {tmp[j++] = a[begin1++];}while (begin2 <= end2) {tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));//将tmp中处理的数据复制到原数组中}printf("\n");gap *= 2;}free(tmp);
}
8. 计数排序
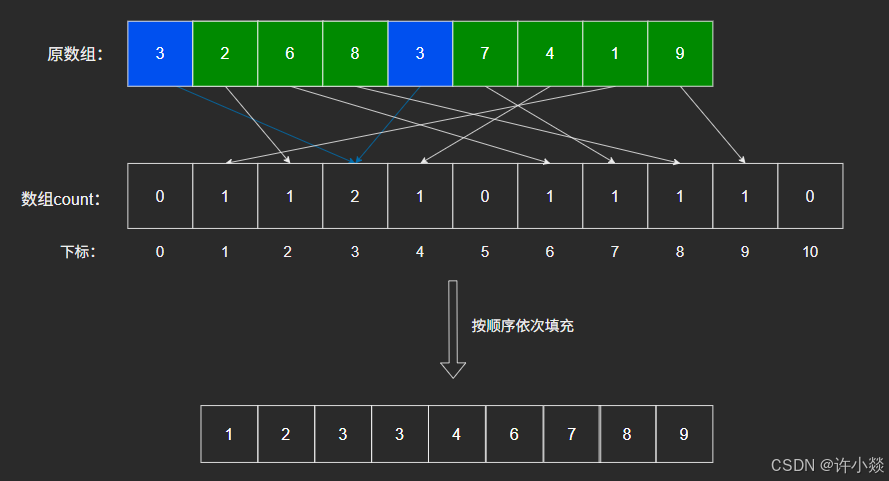
计数排序是一种非比较型的线性时间排序算法,特别适用于 整数数据 且 数据范围较小 的情况。
如图(静态):
动态:
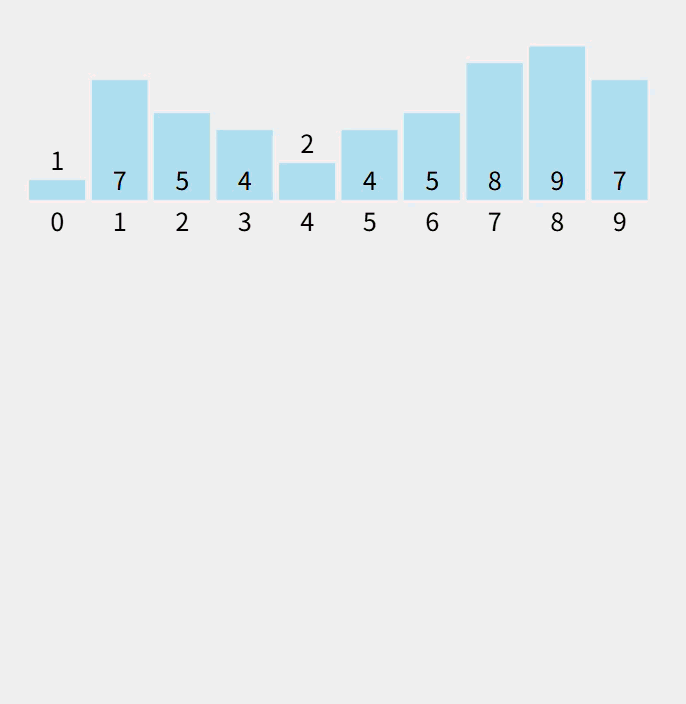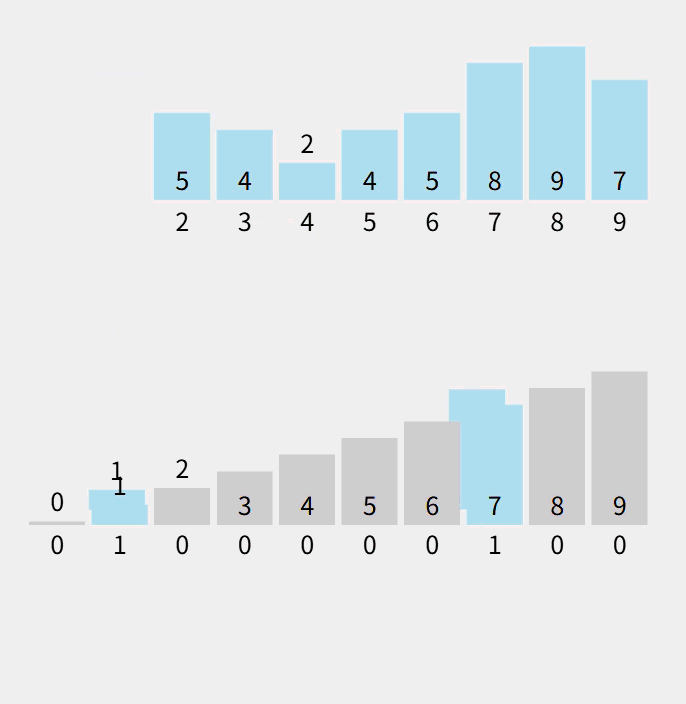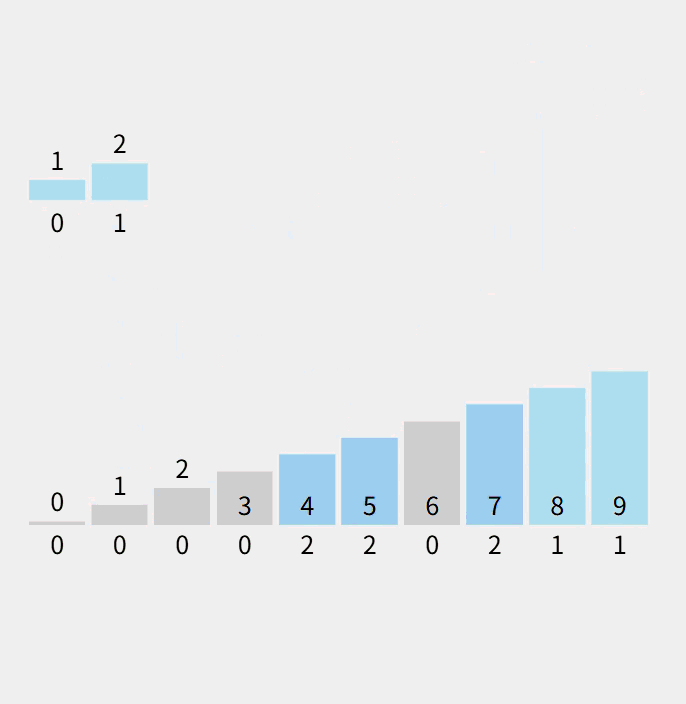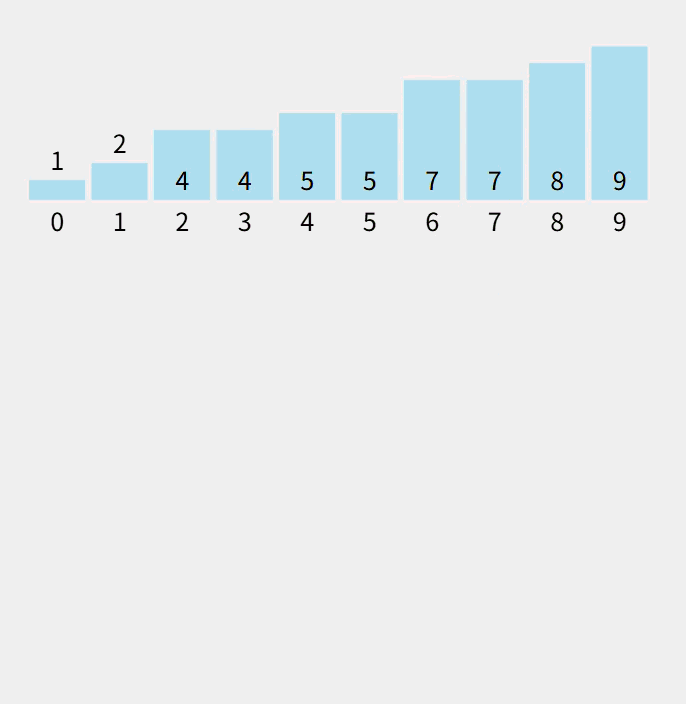
注意:数组count计算的是对应的元素个数。
void CountSort(int* a, int n) {int min = a[0], max = a[0];for (int i = 1; i < n; i++) {if (a[i] < min) {min = a[i];}if (a[i] > max) {max = a[i];}}int range = max - min + 1; //实际需要的元素个数int* count = (int*)calloc(range, sizeof(int)); //开辟空间并初始化为 0 if (count == NULL) {perror("calloc fail!");return;}//统计次数for (int i = 0; i < n; i++) {count[a[i] - min]++; //计算数据个数并放在count数组中,a[i] - min 节省了数组空间 }//排序int i = 0;for (int j = 0; j < range; j++) {while (count[j]--) {a[i++] = j + min; //前面统计时减掉了min ,这里要记得加上}}
}
9. 对比
不同的排序方法各有利弊,需结合实际场景进行选择。
| 排序算法 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n)(优化后) | O(n²) | O(n²) | O(1) | 稳定 |
| 选择排序 | O(n²) | O(n²) | O(n²) | O(1) | 不稳定 |
| 插入排序 | O(n)(基本有序) | O(n²) | O(n²) | O(1) | 稳定 |
| 希尔排序 | O(n log n) | O(n²)(最坏步长) | O(n^1.3) | O(1) | 不稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(n log n) | O(1) | 不稳定 |
| 快速排序 | O(n log n) | O(n²) | O(n log n) | O(log n)(递归) | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | 稳定 |
| 计数排序 | O(n + k) | O(n + k) | O(n + k) | O(n + k) | 稳定 |
-
时间复杂度:
最好:数据已经接近有序时的表现。
最坏:数据完全逆序或极端情况下的表现。
平均:随机数据下的期望表现。
-
空间复杂度:
O(1):原地排序,仅用常数额外空间(如冒泡、选择、插入、希尔、堆排序)。
O(log n):快速排序的递归栈空间。
O(n):归并排序和计数排序需要额外存储空间。
-
稳定性:
稳定:相等元素的相对顺序不变(冒泡、插入、归并、计数排序)。
不稳定:相等元素的顺序可能改变(选择、希尔、堆、快速排序)。
