当前位置： 首页 > news >正文

树状数组的概念、结构及实现

news 2025/7/30 8:45:08

【树状数组的概念】
树状数组（Binary Indexed Tree，简称 BIT）是一种高效处理动态序列“前缀和查询”与“单点更新”的数据结构，由 Peter M. Fenwick 于 1994 年提出‌。结合差分、离散化等技术，树状数组的扩展应用主要体现在“区间修改+单点查询”、“区间修改+区间查询”等方向。而树状数组实现区间修改的核心是通过‌差分思想‌将区间操作转化为单点更新。
在算法竞赛中，树状数组已成为解决逆序对、区间统计等问题的标准工具‌。树状数组通过二进制索引将线性结构转化为隐式树形结构，平衡了空间与时间效率。

【树状数组的结构】
树状数组的经典实现包含两个数组：一个是存储数列元素的数组 a[]，另一个是存储数列前缀和的数组 c[]。而树状数组名称的由来，恰是因为数组 c[] 呈现为树状结构。换句话说，树状数组本质上是一个数组（通常记为 c[]），其逻辑结构通过二进制位的 lowbit 运算隐式构建为一棵多叉树‌。
树状数组示意图，如下所示：

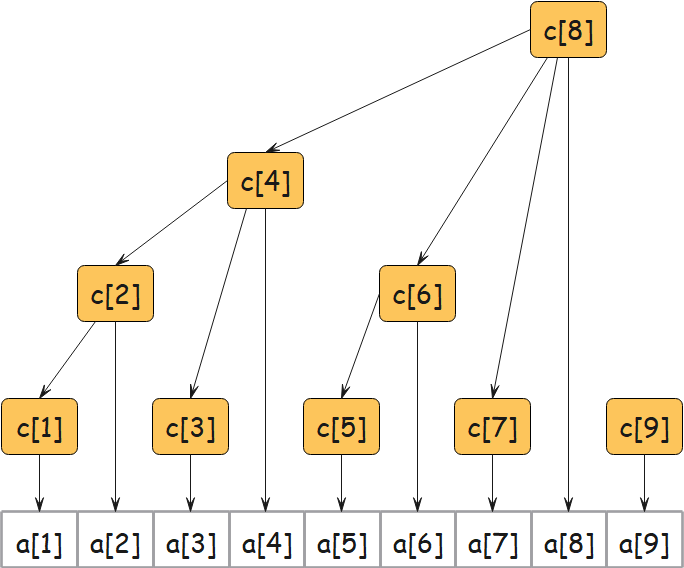
树状数组中 a[] 与 c[] 之间的关系为：c[i]=a[i-2^k+1]+a[i-2^k+2]+…+a[i]，i≥1。其中，k 为序号 i 的二进制表示末尾连续个 0 的个数。显然，数组 c[] 中的每个元素 c[i]，等于数组 a[] 中 i-(i-2^k+1)+1=2^k 个元素的和。例如，序号 8 的二进制表示为 1000，其末尾有 3 个连续的 0，则 c[8] 等于数组 a[] 中 2^3=8 个元素的和，即 c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]。
据上所述，可知在包含 9 个元素的树状数组中，c[i] 与 a[i] 的对应关系如下所示：
c[1]=a[1]
c[2]=c[1]+a[2]=a[1]+a[2]
c[3]=a[3]
c[4]=c[2]+c[3]+a[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=c[5]+a[6]=a[5]+a[6]
c[7]=a[7]
c[8]=c[4]+c[6]+c[7]+a[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
c[9]=a[9]

【树状数组的实现】
（一）lowbit 运算
lowbit 运算 lowbit(i)=i & (-i)=2^k。其中，k 为序号 i 的二进制表示末尾连续个 0 的个数。
需要注意的是，在计算机中，正数的原码、反码、补码相同。负数采用补码表示，且等于负数的反码加 1。所以，lowbit 运算中的 -i 采用‌补码‌表示为 −i=∼i+1。其中 ~i 表示 i 的‌按位取反‌（即 i 的反码）。
例如，若设 i=8（二进制 1000），-i=-8=~8+1（二进制 0111+1=1000），lowbit(8)=1000 & 1000=1000（对应二进制 2^3=8）；若设 i=6（二进制 110），-i=-6=~6+1（二进制 001+1=010），lowbit(6)=110 & 010=010（对应二进制 2^1=2）。

（二）树状数组 c[] 每个元素 c[i] 所包含的数组 a[] 中的元素个数
由上文知，树状数组 c[] 中的每个元素 c[i]，等于数组 a[] 中 i-(i-2^k+1)+1=2^k 个元素的和。又由于 lowbit(i)=i & (-i)=2^k​​​​，所以可得数组 c[] 中的每个元素 c[i] 所包含的数组 a[] 中的元素个数的 C++ 代码就是 lowbit 运算的代码。其中，k 为序号 i 的二进制表示末尾连续个 0 的个数。

int lowbit(int i) {return (-i)&i; //返回树状数组c[]每个元素c[i]所包含的数组a[]中的元素个数
}

（三）树状数组的直接前驱‌与直接后继‌
在树状数组（Fenwick Tree）中，‌直接前驱‌与直接后继‌的定义及计算方式如下所示。
‌1.直接前驱（c[i] 左侧紧邻子树的根）：结点 c[i] 的直接前驱是 c[i-lowbit(i)]，作用‌是用于‌前缀和查询。
2.直接后继（c[i] 的父结点）：结点 c[i] 的直接后继是 c[i+lowbit(i)]，作用‌是用于‌单点更新。
例如，观察上文树状数组的示意图，易知 c[7] 的直接前驱为 c[6]，c[6]的直接前驱为 c[4]，c[4]没有直接前驱；c[5] 的直接后继为 c[6]，c[6] 的直接后继为 c[8]，c[8]没有直接后继。

（四）单点更新
在树状数组中，对某个元素 a[i] 进行修改（如增加 x）时，仅需更新 c[i] 及其所有‌直接后继（父结点）‌，无需遍历整个数组，便可维护 a[] 对应的树状数组 c[] 的变化。单点更新代码如下所示。

void pointUpdate(int i,int val) { //单点更新while(i<=n) {c[i]+=val;i+=lowbit(i);  //c[i]的直接后继（父结点）}
}

例如，观察树状数组的示意图，易知 c[5] 的后继为 c[6]、c[8]，所以若将 a[5] 加 2，则仅需将 c[5] 加 2、c[6] 加 2、c[8] 加 2，便可维护树状数组的变化。

（五）前缀和查询
设 s(i) 表示 a[] 数组中前 i 个元素的前缀和，即 s(i)=a[1]+a[2]+a[3]+...+a[i]，则 s(i) 等于 c[i] 加上 c[i] 的前驱（若 c[i] 没有前驱，则 s[i] 等于 c[i]）。前缀和查询代码如下所示。

int preSum(int i) { //前缀和查询int s=0;while(i>0) { //树状数组的下标从1开始s+=c[i];i-=lowbit(i); //c[i]的直接前驱}return s;
}

为了充分理解前缀和查询的代码，验证如下：
因为 s(i)=a[1]+a[2]+a[3]+...+a[i]，且有
c[1]=a[1]
c[2]=c[1]+a[2]=a[1]+a[2] 
c[3]=a[3]
c[4]=c[2]+c[3]+a[4]=a[1]+a[2]+a[3]+a[4] 
c[5]=a[5]
c[6]=c[5]+a[6]=a[5]+a[6]
c[7]=a[7]
c[8]=c[4]+c[6]+c[7]+a[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]
c[9]=a[9]
所以 s(1)=a[1]=c[1]     → c[1] 没有前驱
s(2)=a[1]+a[2]=c[2]     → c[2] 没有前驱
s(3)=a[1]+a[2]+a[3]=c[3]+c[2]     → c[3] 的前驱是 c[2]
s(4)=a[1]+a[2]+a[3]+a[4]=c[4]     → c[4] 没有前驱
s(5)=a[1]+a[2]+a[3]+a[4]+a[5]=c[5]+c[4]     → c[5] 的前驱是 c[4]
s(6)=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]=c[6]+c[4]     → c[6] 的前驱是 c[4]
s(7)=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]=c[7]+c[6]+c[4]     → c[7] 的前驱是 c[6]、c[4]
s(8)=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]=c[8]     → c[8] 没有前驱
s(9)=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]+a[9]=c[9]+c[8]     → c[9] 的前驱是 c[8]
综上，验证了“s(i) 等于 c[i] 加上 c[i] 的前驱（若 c[i] 没有前驱，则 s[i] 等于 c[i]）”的结论。

（六）区间查询
树状数组（Fenwick Tree）的‌区间查询‌，即树状数组的区间和查询。
若求数组 a[] 的区间 [i,j] 中元素的和 a[i]+a[i+1]+…+a[j]，则利用前缀和思想可得数组 a[] 的区间 [i,j] 中的元素和为 preSum(j)-preSum(i-1)。
因为，preSum(j)=a[1]+a[2]+…+a[i-1]+a[i]+…+a[j]，preSum(i-1)=a[1]+a[2]+…+a[i-1]。
所以，preSum(j)-preSum(i-1)=a[i]+a[i+1]+…+a[j]，故得证。
树状数组区间查询的代码如下所示。

int segSum(int i,int j) { //区间查询return preSum(j)-preSum(i-1);
}

（七）区间更新
● 树状树状的“区间更新”操作，通常指将区间 [i,j] 中的每个元素 a[i] ~ a[j] 都加 k。
树状数组的‌“区间更新”操作通常通过‌差分数组‌实现，核心思想是将“区间更新”转化为两次“单点更新”。从而将“区间更新、单点查询”问题，转换为树状数组擅长的“单点更新、区间查询”问题。
此解题思想利用了一维差分的性质：对原数组 a 的区间 [le, ri] 中每个元素 +x 等价于对其差分数组 d 的区间端点执行 d[le]+=x，d[ri+1]-=x。
示例：对原数组 a[]=[3 5 9 10 16 18 27] （下标从 1 开始）区间 [2,5] 中的每个数都加 3，等价于对其差分数组 d[] 执行 d[2]+=3，d[5+1]-=3。
解析：由 d[1]=a[1]，d[i]=a[i]-a[i-1]，i≥2 可得，原数组 a[]=[3 5 9 10 16 18 27] 的差分数组为 d[]=[3 2 4 1 6 2 9]。执行 d[2]+=3，d[5+1]-=3 后，原数组的差分数组由 d[]=[3 2 4 1 6 2 9] 变为 d[]=[3 5 4 1 6 -1 9]。显然，此时由关系 d[1]=a[1]，d[i]=a[i]-a[i-1]，i≥2，知：
a[1]=d[1]=3，
a[2]=d[2]+a[1]=5+3=8，
a[3]=d[3]+a[2]=4+8=12，
a[4]=d[4]+a[3]=1+12=13，
a[5]=d[5]+a[4]=6+13=19，
a[6]=d[6]+a[5]=-1+19=18，
a[7]=d[7]+a[6]=9+18=27。
易见，对原数组 a[]=[3 5 9 10 16 18 27] （下标从 1 开始）执行 d[2]+=3，d[5+1]-=3 后，原数组由 a[]=[3 5 9 10 16 18 27] 变为 a[]=[3 8 12 13 19 18 27]，即原数组区间 [2,5] 内的每个元素确实都加了 3。
证明详见：https://blog.csdn.net/hnjzsyjyj/article/details/145616810

● 树状数组“区间更新”的代码，个人在编码实践中一般不写为函数，而是在主函数中直接构建。
树状数组“区间更新”的代码，通常由如下两部分代码：
（1）构造差分数组

int val,pre=0;
for(int i=1; i<=n; i++) { //下标从1开始scanf("%d",&val);pointUpdate(i,val-pre); //构造差分数组 d[]的树状数组pre=val;
}

（2）两次“单点更新”操作

scanf("%d%d%d",&u,&v,&w);
pointUpdate(u,w);
pointUpdate(v+1,-w);


【树状数组的示例】
如下两个示例代码的 main() 函数外的部分，完全一样。main() 函数内的部分，依据问题个性化构建。
（示例一）洛谷 P3374：【模板】树状数组 1：https://blog.csdn.net/hnjzsyjyj/article/details/120575823

#include <bits/stdc++.h>
using namespace std;const int maxn=5e5+5;
int c[maxn];
int n,m;int lowbit(int i) {return (-i)&i; //返回树状数组c[]每个元素c[i]所包含的数组a[]中的元素个数
}void pointUpdate(int i,int val) { //单点更新while(i<=n) {c[i]+=val;i+=lowbit(i);  //c[i]的直接后继（父结点）}
}int preSum(int i) { //前缀和查询int s=0;while(i>0) { //树状数组的下标从1开始s+=c[i];i-=lowbit(i); //c[i]的直接前驱}return s;
}int segSum(int i,int j) { //区间查询return preSum(j)-preSum(i-1);
}int main() {scanf("%d%d",&n,&m);memset(c,0,sizeof(c));int val;for(int i=1; i<=n; i++) { //下标从1开始scanf("%d",&val);pointUpdate(i,val); //构建树状数组}while(m--) {int k,u,v,x;scanf("%d",&k);if(k==1) {scanf("%d%d",&u,&x);pointUpdate(u,x);} else {scanf("%d%d",&u,&v);printf("%d\n",segSum(u,v));}}return 0;
}/*
in：
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4out：
14
16
*/


 （示例二）洛谷 P3368：【模板】树状数组 2：https://blog.csdn.net/hnjzsyjyj/article/details/120573850

#include <bits/stdc++.h>
using namespace std;const int maxn=5e5+5;
int c[maxn];
int n,m;int lowbit(int i) {return (-i)&i; //返回树状数组c[]每个元素c[i]所包含的数组a[]中的元素个数
}void pointUpdate(int i,int val) { //单点更新while(i<=n) {c[i]+=val;i+=lowbit(i);  //c[i]的直接后继（父结点）}
}int preSum(int i) { //前缀和查询int s=0;while(i>0) { //树状数组的下标从1开始s+=c[i];i-=lowbit(i); //c[i]的直接前驱}return s;
}int segSum(int i,int j) { //区间查询return preSum(j)-preSum(i-1);
}int main() {scanf("%d%d",&n,&m);memset(c,0,sizeof(c));int val,pre=0;for(int i=1; i<=n; i++) { //下标从1开始scanf("%d",&val);pointUpdate(i,val-pre); //构造差分数组 d[]的树状数组pre=val;}while(m--) {int k,u,v,w;scanf("%d",&k);if(k==1) {scanf("%d%d%d",&u,&v,&w);pointUpdate(u,w);pointUpdate(v+1,-w);} else {scanf("%d",&u);printf("%d\n",preSum(u));}}return 0;
}/*
in：
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4out：
6
10
*/





【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/120559543
https://blog.csdn.net/hnjzsyjyj/article/details/120575823
https://blog.csdn.net/hnjzsyjyj/article/details/120573850
https://blog.csdn.net/hnjzsyjyj/article/details/145618311
https://blog.csdn.net/hnjzsyjyj/article/details/145282546
https://blog.csdn.net/hnjzsyjyj/article/details/145268744
https://blog.csdn.net/hnjzsyjyj/article/details/145616810



 

http://www.dtcms.com/a/302856.html

相关文章：

  • 塔能科技物联运维平台及城市照明市场竞争力分析
  • 国产测试用例管理工具横向评测：DevOps时代如何选择最适合的协作平台？
  • window显示驱动开发—RecycleCreateCommandList
  • Angular 依赖注入
  • 网络 编程
  • 洛谷刷题7.28
  • 基于AFLFast的fuzz自动化漏洞挖掘(1)
  • 【HTTP】防XSS+SQL注入：自定义HttpMessageConverter过滤链深度解决方案
  • 【React Context API 优化与性能实践指南】
  • DBAPI 实现分页查询的两种方法
  • 阿里云Ubuntu 22.04 ssh隔一段时间自动断开的解决方法
  • 【力扣热题100】哈希——两数之和
  • 【mysql】—— mysql中的timestamp 和 datetime(6) 有什么区别，为什么有的地方不建议使用timestamp
  • 智能制造，从工厂建模，工艺建模，柔性制造，精益制造，生产管控，库存，质量等多方面讲述智能制造的落地方案。
  • 破解PCB制造痛点，盘古信息IMS MOM 铸就数字化标杆工厂
  • PL/SQL
  • 开疆智能ModbusRTU转Profinet网关连接西门子CP341配置案例
  • DDD之整体设计流程(2)
  • debian系统分卷是不会影响系统启动速度？
  • 排序算法 (Sorting Algorithms)-Python示例
  • Android 系统架构
  • 阿里云 API 网关 x OKG：游戏连接治理的「最后一公里」
  • 阿里云正式开源 LoongSuite：打造 AI 时代的高性能低成本可观测采集套件
  • 电脑不小心误删了文件怎么恢复？？
  • AI资讯日报 - 2025年07月28日
  • EXCEL批量生成超链接引用无效的情况
  • Kotlin中Flow
  • 基于Spring Boot的装饰工程管理系统(源码+论文)
  • 一个典型的微控制器MCU包含哪些模块？
  • kafka开启Kerberos使用方式