当前位置：首页 > news >正文

【机器学习】第七章特征工程

news 2025/7/28 7:22:01

在现实的数据集中，数据往往不是那么完美，需要进行数据预处理和特征工程。数据预处理和特征工程都是对数据的处理，只不过数据预处理对数据进行归一化、离散化、缺失值处理、去除共线性等，而特征工程通过特征提取、特征选择、降维等把数据处理成可更直接地被使用的数据。原始的数据，如果不加以处理，直接用于机器学习，那么最后得出的结果可能会令人不太满意。“数据和数据特征决定了机器学习的上限，而模型和算法只用于逼近这个上限而已”，对于一种确定的算法，数据的优劣可能直接决定了算法最终的效果，而这里的数据则是经过特征工程处理得到的数据。特征工程是指将所收集到的原始数据通过一系列的处理转化成适合所构建的模型的训练数据，从而使算法最终的结果不断逼近上限，提高模型的性能。

7.1特征提取

前文介绍了特征提取前的数据预处理等方面的工作，接下来将对如何进行特征提取这个问题进行深入探讨。特征提取主要包括字典特征提取、文本特征提取和图像特征提取这3个方面。“万物皆可为特征”，因此特征的种类和数量无穷无尽。针对不同种类的特征采取不同的特征提取方法，往往会对问题的研究有所帮助。

7.1.1 字典特征提取

如果要对所需要的数据进行特征提取，但这些数据恰巧都被单独存储在一个字典里，例如学生的成绩、城市的交通数据、书籍的书号等。如果对这些数据进行直接提取，那么过程会非常复杂。特别是当数据量非常大的时候，稍有不慎，提取出的数据就可能会出错，导致研究的问题出现错误的结果。

这时可以借助sklearn库的feature_extraction中的DictVectorizer()（字典矢量器)。DictVectorizer(的作用是对特征进行特征值化，即保留连续特征并为离散特征创建虚拟变量。例如以下数据（随机数据)：

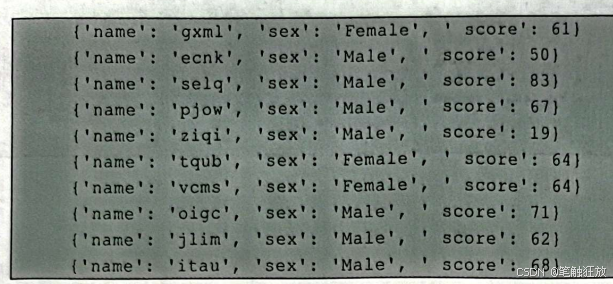
这是随机构建的一组关于学生成绩的随机数据（在此省略构造数据的过程）。可以看到，每一个学生的信息都被存放在一个单独的字典里。因此，首先将所有学生的信息都存放在一个列表中（即转化成字典列表），然后就可以用DictVectorizer(方法对其进行特征提取。

由于DictVectorizer（）默认返回的是一个稀疏矩阵，为了使输出结果更直观，将sparse的值设置为 False：

其中dit中存放的是由每个学生信息所构成的字典列表。输出结果：

在这里可以看到，输出结果中的每一行即为一个学生的信息，例如第1行的学生的姓名是gxml”，性别是“Female”，成绩是“61”分。

7.1.2 文本特征提取

在特征提取中，文本特征提取所占有的地位非常重要。文字是人类文化传承的重要载体之一，如果想在机器学习领域中有所建树，那么掌握文本特征提取便是必不可少的技能之一。文本是由单词、短语和句子组成的自由化的组合，其形式多种多样，但总是可以被转换为结构化数据特征。通过文本特征提取，可以分析两段不同文本间的相似度，还可以提取整篇文章的关键词和主题，也可以对文章进行感情色彩分析等。

但是，在进行文本特征提取时，首先要对文本进行预处理，使得所提取的特征能更好地被使用。对文本的预处理方法主要有删除特殊字符（即非字母或数字的字符）、删除停止词（即意义不大却出现频率较高的一类词，例如，“a”“an”“the”“of”等）、扩展缩略语（将单词或音节转换成对应的缩写形式，使得文本更为标准化，例如将“are not”转换成“aren't”）和词根提取与词根还原（即将表示同一个意思的单词转换成对应的词根形式进行存储，使得文本更为标准化，同时也可节约存储空间，例如，“beauty”“beautiful”“beautifully”都表示漂亮、美丽的意思，因此只需对“beauty”进行存储，就可以将所要表达的意思记录下来）等。

例如，对下面的一段短文进行文本特征提取。

首先，要将这一段短文输入，并利用正则表达式将其分割：

将这一整段短文分割成单词后，发现其中有一些单词是不需要的，例如“is”“of”等，因此需对其进行一些处理，仅保留需要的单词：

根据预先设置好的停止词库来删除不需要的单词：

读者可能会认为这种处理方式非常麻烦，别担心，还有简单的处理方式，如果真的要对文章进行处理，还要用到Python中的NLTK库。NLTK库是专门用来处理自然语言的工具，第9章将对其进行详细介绍。（1）词袋模型可以将文本装进词袋模型中去处理。词袋模型可以形象化地理解成把文本分成词，然后用一个“袋子”来装这些词，这种表现方式不考虑文法以及词的顺序。接下来将介绍3种词袋模型。

CountVectorizer是sklearn库中feature_extraction中的一个常见的特征数值计数类，其作用是将文本转化成词频矩阵。代码如下：

这里得到的输出结果是一个稀疏矩阵，由于篇幅较长，这里只展示部分结果：

（2）N-Grams 袋模型 N-Grams袋模型是词袋模型的一个扩展，被用来统计按顺序出现的单词或短语的出现频率。N-Grams 的初始模型是一个m*n的矩阵，m表示文档的数量，n表示短语的长度。例如，调查一个由3个单词组成的短语在文章中的出现频率，就可以通过设置CountVectorizer中的ngram_range=(3,3)来实现。但是要注意，N-Grams 统计的是文章中删除停止词后连续的单词。代码如下：

(3)TF-IDF 模型 TF-IDF模型被用来解决文章中某些出现频率较小的词语被出现频率较大的词语掩盖的问题，是信息检索和自然语言处理领域中不可或缺的模型之一。举个例子，有一篇大量谈论A喜欢吃什么的文章，要从中提取A这个人喜欢吃的都有什么。假设A喜欢吃烤鸭、白菜、油条、豆浆、西红柿和馒头，且A顿顿都吃馒头。所以在这篇文章中，通常馒头这个词语出现的频率会高于其他几个词语出现的频率。那么，在文章足够多的情况下，可能馒头这个词语出现的频率会高达99%，从而认为馒头是A喜欢吃的，而烤鸭、白菜等被作为干扰项而排除。其计算方法为:

其中，S代表词语x的得分，TF(x)代表词语x的词频，IDF(x)代表逆向文档频率。逆向文档频率（inverse document frequency，IDF）是词语普遍重要性的度量，计算方法为：

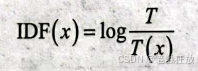
其中，T代表文章总数量，T(x)代表含有词语x的文章数量。但是，如果T(x)=0，就会使IDF(x)变得没有意义。所以，还要对IDF(x)做平滑处理。常见的IDF(x)平滑处理公式：

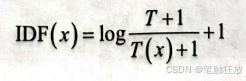
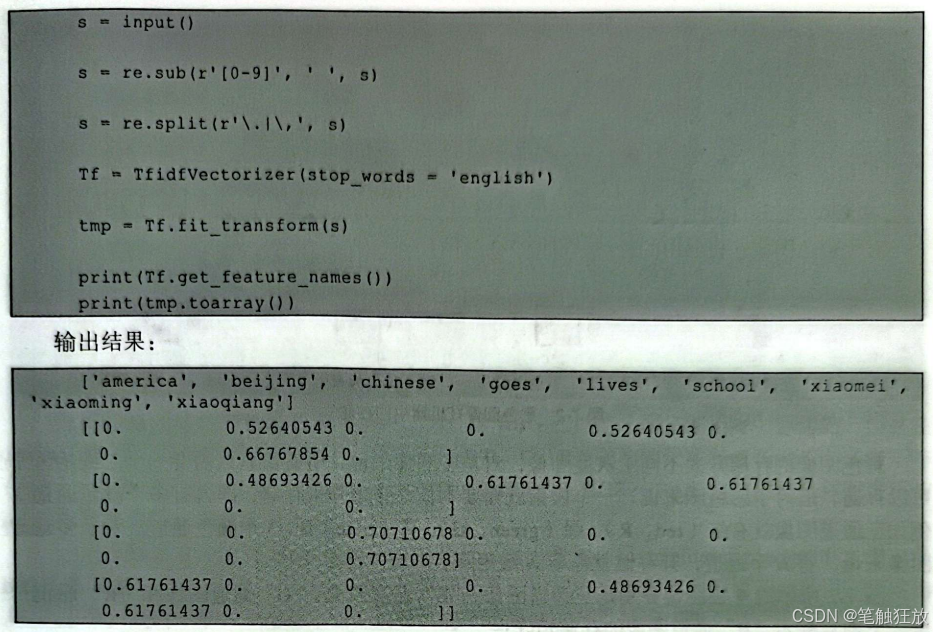
通过分析数据可以得知，在第一句话“Xiaoming lives in Beijing。”中，“Xiaoming”占比约为0.66767854，“lives”占比约为0.52640543,“beijing”占比约为0.52640543。还可以借助CountVectorizer和TfidfTransformer实现和上述代码相同的效果：

7.1.3 图像特征提取

在日常生活中，图像是除文字外的又一重要的信息载体，目前的图像处理技术同样也离不开图像特征提取。在讲解如何提取图像特征之前，首先要知道什么是图像及图像在机器中是如何存储的。

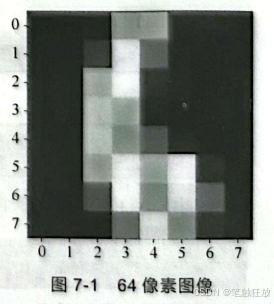
以图7-1为例，可以看到这幅图像是由64（8×8）个小方格组成的，一个小方格表示一个像素，图7-1所示的图像就包含64像素。

仔细看图7-1，可以发现小方格有的白一点，有的黑一点，可以用一个数值来量化其颜色，越黑则数值越小（纯黑为0），越白则数值越大（纯白为1），这样整幅图像就可以转化成二维矩阵的形式在机器中存储。这就是这类图像在机器中的存储方式。

下面这个二维矩阵就是图像在机器中存储的结果，其中的数值代表灰度，这类图像通常被称为灰度图像。

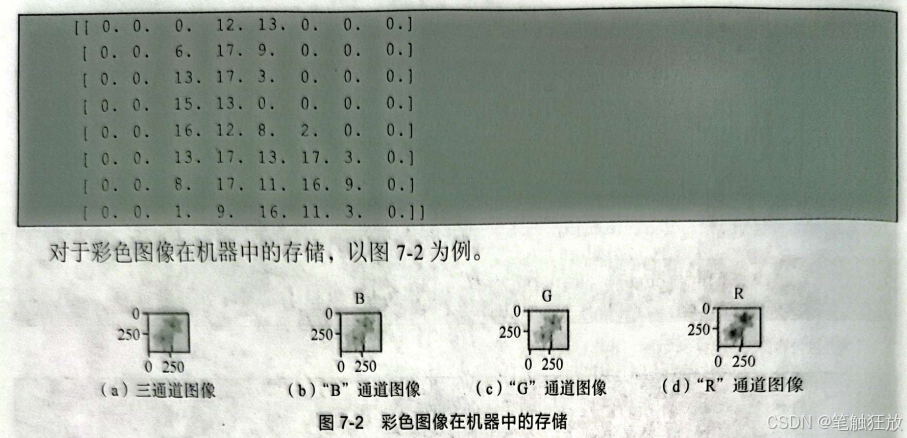
彩色图像的存储方式不同于灰度图像，对灰度图像来说，所有像素只需要一个二维矩阵就可以存储、但对于彩色图来说，一个像素就需要不止一个矩阵来存储，即含有多个颜色通道，例如三通道图像就有红（red,R)绿（green，G)、蓝（blue，B）3个颜色通道。对于多通道图像来说，有N个通道，其存储就需要N维矩阵。

图7-2所示的4幅图像分别是三通道图像、“B”通道图像、“G”通道图像和“R”通道图像。下面只展示“B”通道图像的存储矩阵：

讲解了图像在机器中如何存储之后，下面介绍简单的图像操作。本书对图像的处理采用的是Python中的OpenCV库，当然能对图像进行处理的不止这一个库，例如还有 scikit-image等、本书不再详细介绍，有需要的读者请自行查阅。

我们知道，对于JPG彩色图像来说，其是以RBG三通道（即三维矩阵）存储的，但是在OpenCV2中、图像的颜色通道的排列顺序却是B、G、R，把它转化成灰度图像（以二维矩阵存储)，就要对其进行压缩，而cv.cvtColor(tp，cv.COLOR_BGR2GRAY)的作用就是将图像压缩成二维矩阵（转化成灰度图像）。

这里提醒读者，使用matplotlib.pyplot也可以输出图片，但pyplot.imshow(的默认接口是RGB格式的，也就是说，pyplot.imshowO只能正常输出三维矩阵构成的图像，如果用它来输出灰度图像，就会产生一些意想不到的效果，感兴趣的读者可以试一下。

下面以图7-3所示的灰度图像为例，讲解如何提取像素值特征。

0的作用是以灰度图像的形式读入图像。

我们知道，一幅图像是由若干个像素组成的，且每个像素都有自己的值（灰度）。所以可以将每一个像素看作一个单独的特征，那么一幅图像就有N×M个特征（N代指图像的长，M代指图像的宽），所以接下来只要知道这幅图像有多少个像素就可以知道这幅图像有多少个特征。

7.2 特征选择

当特征经过预处理和特征提取之后，我们就应该思考一个问题：如何选择对我们最有意义的特征？在未进行模型训练之前，可不可以消除一些无关紧要的特征使得我们所构建的模型具有更好的泛化能力？而这就涉及即将要讲解的特征选择。

7.2.1 Filter

Filter（过滤）根据特征在各种统计检验中的得分以及与目标的相关性来进行特征选择。从方差的角度考虑，如果一个特征的方差为0，就可以毫不客气地把这个特征消除。特征的方差越小，说明这个特征在我们所研究的模型中基本相同，甚至取值也相同，那么可以把这个无关特征消除。

VarianceThreshold(方差过滤，是Filter中常用的一个方法，也是sklearn.feature_selection中的一个方法。

可以看到，VarianceThresholdO消除了出现概率大于0.6即方差小于0.6×(1-0.6)=0.24的特征。

如果从相关性的角度考虑，研究单一特征对目标的相关性来进行特征选择，那么将从以下两个方面进行考虑：如果研究目标为离散特征（回归问题），可以使用卡方检验来进行特征选择；如果研究目标为连续特征（分类问题），可以使用皮尔逊相关系数和最大信息系数来进行特征选择。接下来以sklearm自带的乳腺癌数据集为例，分别演示上述方法的代码实现。

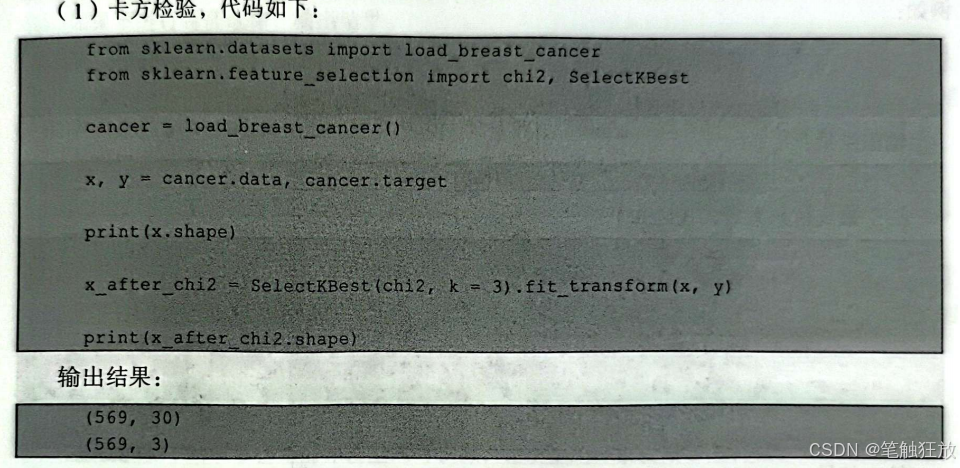
可以看到，经过卡方检验后，选出了3个最优的特征，其中SelectKBestO中k的作用是调节选出的特征的数量，这里设置的是k=3。

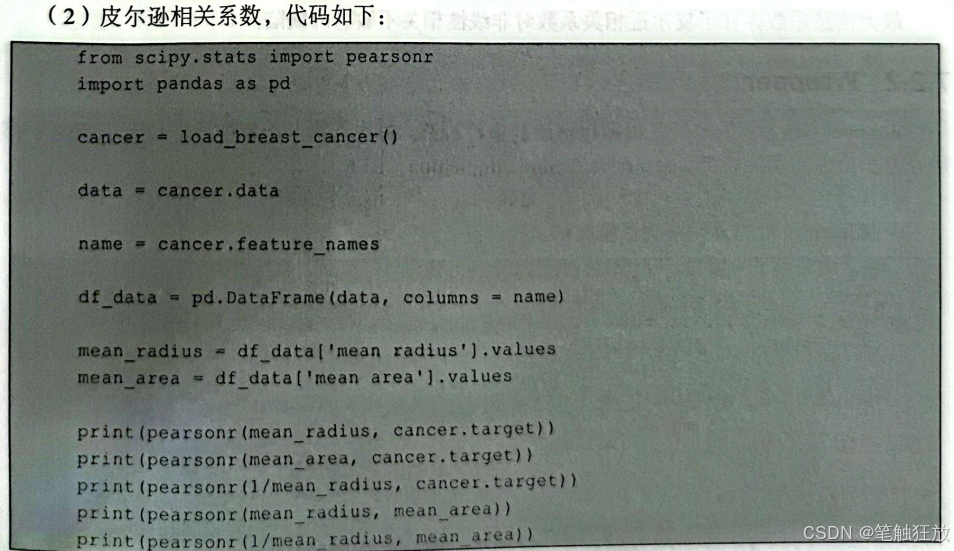
皮尔逊相关系数输出的是一个二元组(score,p-value)，其中score的取值为[-1,1]，score 的值越接近1表示具有正相关，0表示不相关，一1表示具有负相关。

但是，皮尔逊相关系数还有一个明显的缺陷：只对线性相关敏感，对非线性相关则不敏感。

最大信息系数弥补了皮尔逊相关系数对非线性相关不敏感的缺陷。

7.2.2 Wrapper

Wrapper（包装）的原理是根据目标函数进行训练，每次选择若干特征或排除若干特征，常用的方法是递归消除特征(recursive feature elimination,RFE)。 RFE选定一个基模型进行多轮训练，每轮训练过后，消除若干特征，再重新进行下轮训练。以sklearn自带的鸢尾花数据集为例实现：

可以看到，使用RFE进行递归消除特征，得到的精度比没有使用RFE得到的精度反而要好很多。这里n_feature_to_select的取值为[1,特征数]，estimator的取值为所选择的基函数。

当然也可以查看递归消除特征后选择的新特征：

7.2.3 Embedded

Embedded（嵌入）让特征和模型同时训练，让模型选择去使用哪些特征。其原理是先让特征在模型中训练，利用训练得到的各项特征的权值系数按照从大到小的原则去选择特征，一般选取能对特征进行打分的模型来进行特征选择。

这里，利用sklearn.feature_selection中SelectFromModel进行特征选择。实现如下。

（1）基于L1的特征选择

以 sklearn 中的wine 数据集为例：

可以看到，基于L1的特征选择舍弃了5个特征。

(2）基于随机森林的特征选择

代码如下:

7.3 降维

通常情况下，通过特征提取得到的特征往往都是冗余和复杂的，特征数量达到几十或者几百。在这种情况下，即使对特征进行预处理和特征选择，用得到的新特征进行机器学习，模型的泛化能力可能仍然达不到理想的标准。而且，特征（维度）越多，能用于机器学习的样本就越少，并且在高维空间中的计算也成了一个很大的难题。

降维是指将高维度的数据经过有限次变换，转变成低维度的数据，从而使数据能更好地应用在机器学习上，得到一个更好的结果。降维是对高维度数据进行预处理的方法，对高维度的数据保留最重要的一些特征，去除噪声和不重要的特征，从而达到提升数据处理速度的目的。

在实际的生产和应用中，降维在一定的信息损失范围内，可以节省大量的时间和成本。降维也是应用非常广泛的数据预处理方法。

降维的算法有很多，例如 PCA、独立成分分析（independent component analysis，ICA)线性辨别分析（linear discriminant analysis,LDA）等。PCA和ICA是无监督学习算法，而LDA是监督学习算法。本节只对PCA进行详细讲解，对LDA进行简单介绍。

在对数据进行归约的时候简单提到了PCA。PCA还是最常用的线性降维方法之一，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留较多的原数据的特性。

如果只通过映射把所有的点都映射到一起，那么几乎所有的信息都丢失了，而如果映射后方差尽可能大，那么数据点则会分散开来，以此来保留更多的信息。PCA追求的是在降维之后能够最大化地保留数据的内在信息，并通过衡量在投影方向上的数据方差的大小来衡量该投影方向的重要性。可以证明，PCA是丢失原始数据信息最少的线性降维方式之一。代码如下:

可以看到现在有500个数据、10个特征。然后利用PCA降维：

可以清楚地看到现在只有2个特征（主成分）了。为什么要进行降维？因为这样可以进行数据可视化，方便我们理解。下面通过降维对数据集进行可视化：

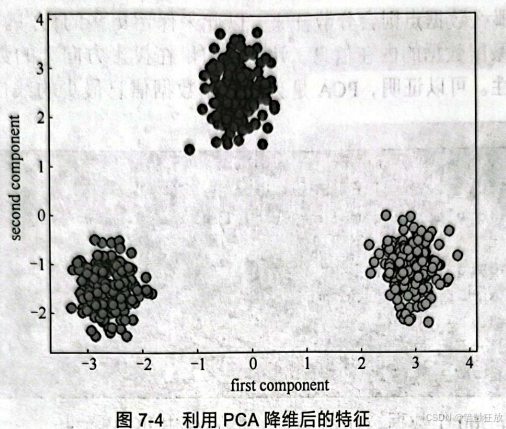
那降维后的特征与原特征有什么关系呢？让我们看图7-5。图中表明将10个特征转化成了2个特征：first component（第一特征）和second component（第二特征)。

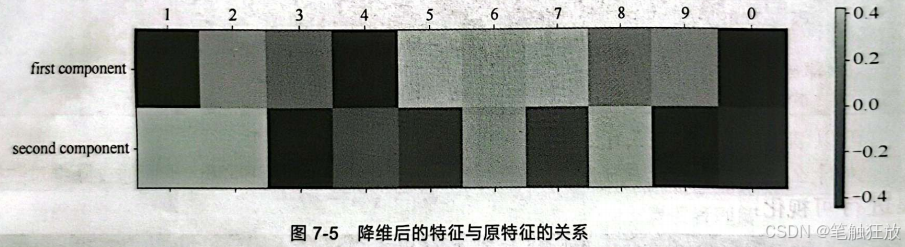
这10个特征转化成的2个特征即2个主成分，图7-5右侧所示颜色代表了数值，转化前的特征与转化后的主成分对应的值为正数为正相关，为负数则为负相关。

以sklearn中的wine数据集为例，直接看其实现：

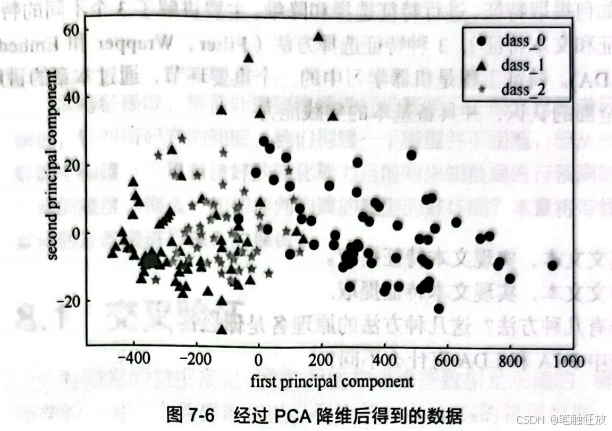
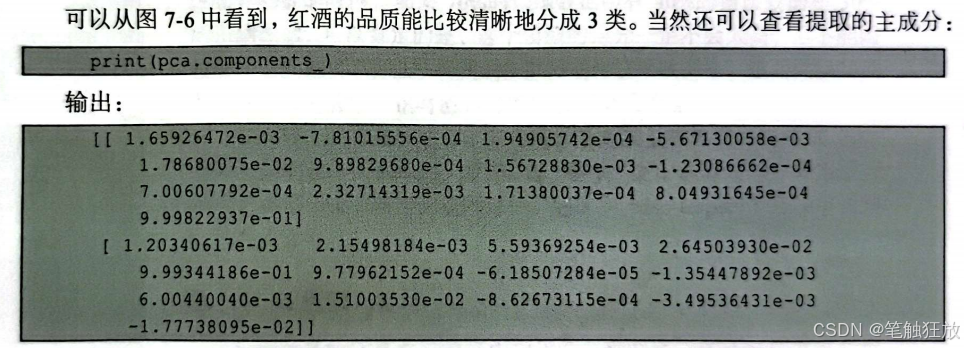
降维的优点是使数据集更容易使用、可去除噪声、方便理解、无参数限制、可降低计算难度等，缺点是投影以后对数据的区分作用并不大，反而可能使数据杂糅在一起而无法区分。在数据分布是非高斯分布的情况下，使用PCA方法得出的主成分可能不是最优的。

在实际情况中，有些数据可能并不服从高斯分布，而是服从超高斯分布的，这意味着随机变量更频繁地在零附近取值。与相同方差的高斯分布相比，超高斯分布的图形在零点处更“尖”。在非高斯分布的情况下PCA得到的主成分可能并不是最优解，这时候不能用方差作为衡量标准，可以使用维度间的正交假设，即ICA。ICA与其他方法的重要区别在于，它寻找满足统计独立和非高斯的成分。

PCA和ICA都是无监督学习的降维算法，而LDA是一种监督学习的降维算法，也就是说它的数据集的每个样本是有类别输出的。LDA算法既可以用于降维，又可以用于分类，但是目前来说，主要还是用于降维。在进行图像识别相关的数据分析时，LDA是一个有力的工具。LDA的原理可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。即要将数据在低维度上进行投影，投影后希望同一类别数据的投影点尽可能接近，而不同类别数据的类别投影中心尽可能远。LDA在样本分类信息依赖均值而不是方差的时候，比PCA等算法的效果较优。但 LDA 也不适合对非高斯分布样本进行降维。

7.4 小结

本章介绍了如何提取特征、进行特征选择和降维。主要讲解了3个不同的特征提取方面（字典特征、图像特征和文本特征)3种特征选择方法（Filter、Wrapper和Embedded）和2种降维算法（PCA、LDA)。特征工程是机器学习中的一个重要环节，通过本章的讲解，希望读者对以上内容有较为全面的认识，并具备基本的实践能力。