数据结构--优先级队列(堆)
一.优先级队列
概念:队列的元素是遵循先进先出的原则,而优先级队列是优先级最高的先出队列
二.堆
概念:
对一个集合元素,堆是按照完全二叉树的顺序存储方式把数据存储到一维数组中
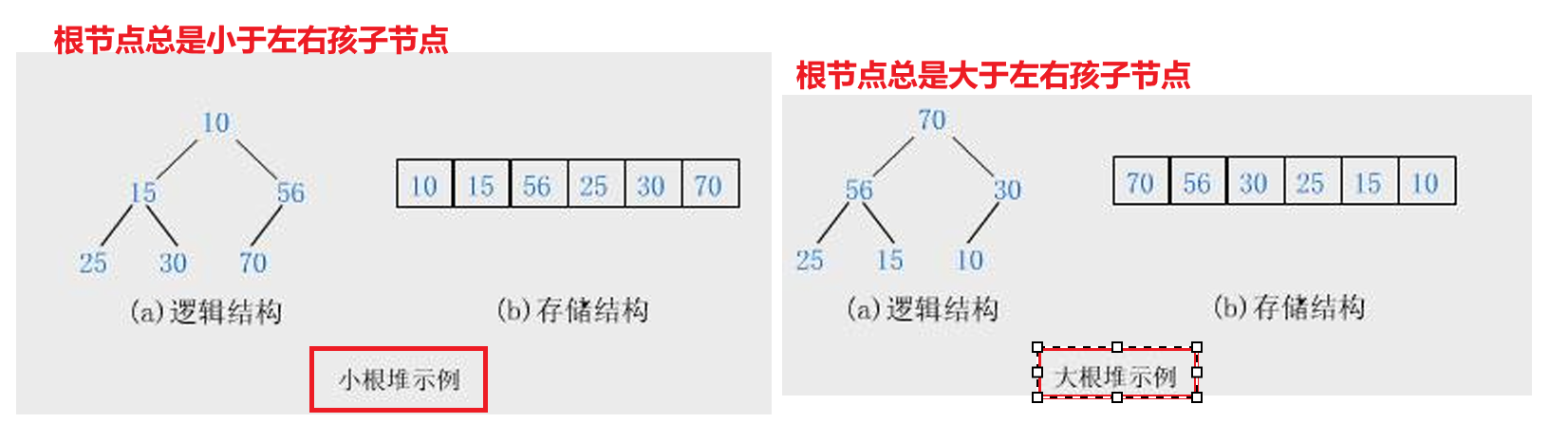
分为大根堆和小根堆
图像:
性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
三.大小堆的模拟实现
可以分为向上和向下过程分为俩种模式
向下过程:
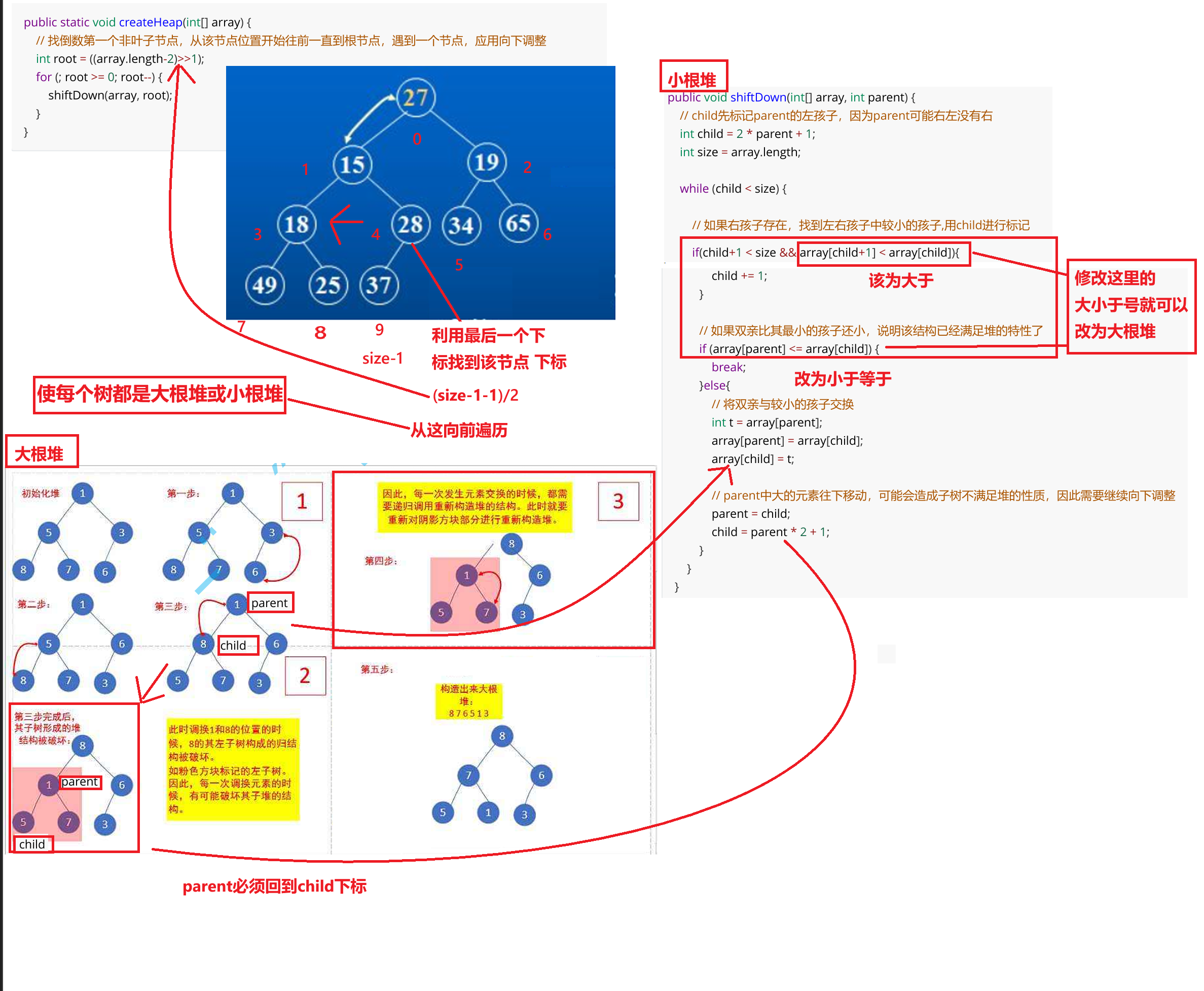
向上过程:
public void shiftUp(int child){int pre =(child-1)/2;while (pre >= 0) {if(elem[pre]<elem[child]){swap(elem,child,pre);child=pre;pre=(child-1)/2;}else {break;}}}四.PriorityQueue的模拟实现
public void offer(int value){if(isFull()){grow();}elem[size]=value;shiftUp(size);size++;}public int poll(){if(isEmpty()){return -1;}int ret =elem[0];size--;swap(elem,0,size);shiftDown(0,size);return ret;}public int peek(){if (isEmpty()){return -1;}return elem[0];}注意:
利用以上的offer方法(向上过程)就可以创建堆
原理:在一个大根堆或小根堆最后一个空间插入,再向上过程(shifup),就形成了大根堆或小根堆
poll方法原理:将0下标和未下标的值交换位置,尾下标向前一位,在对0这棵树进行调整
优点:由于之前为大根堆或小根堆,交换位置后,只要0下标这棵树不是小根堆或大根堆,只需要向下调整0下标这颗大树即可就能转化为小根堆或大根堆
五.向下过程和向上过程创建堆的复杂度

六.堆排序
过程:
1. 建堆
升序:建大堆
降序:建小堆
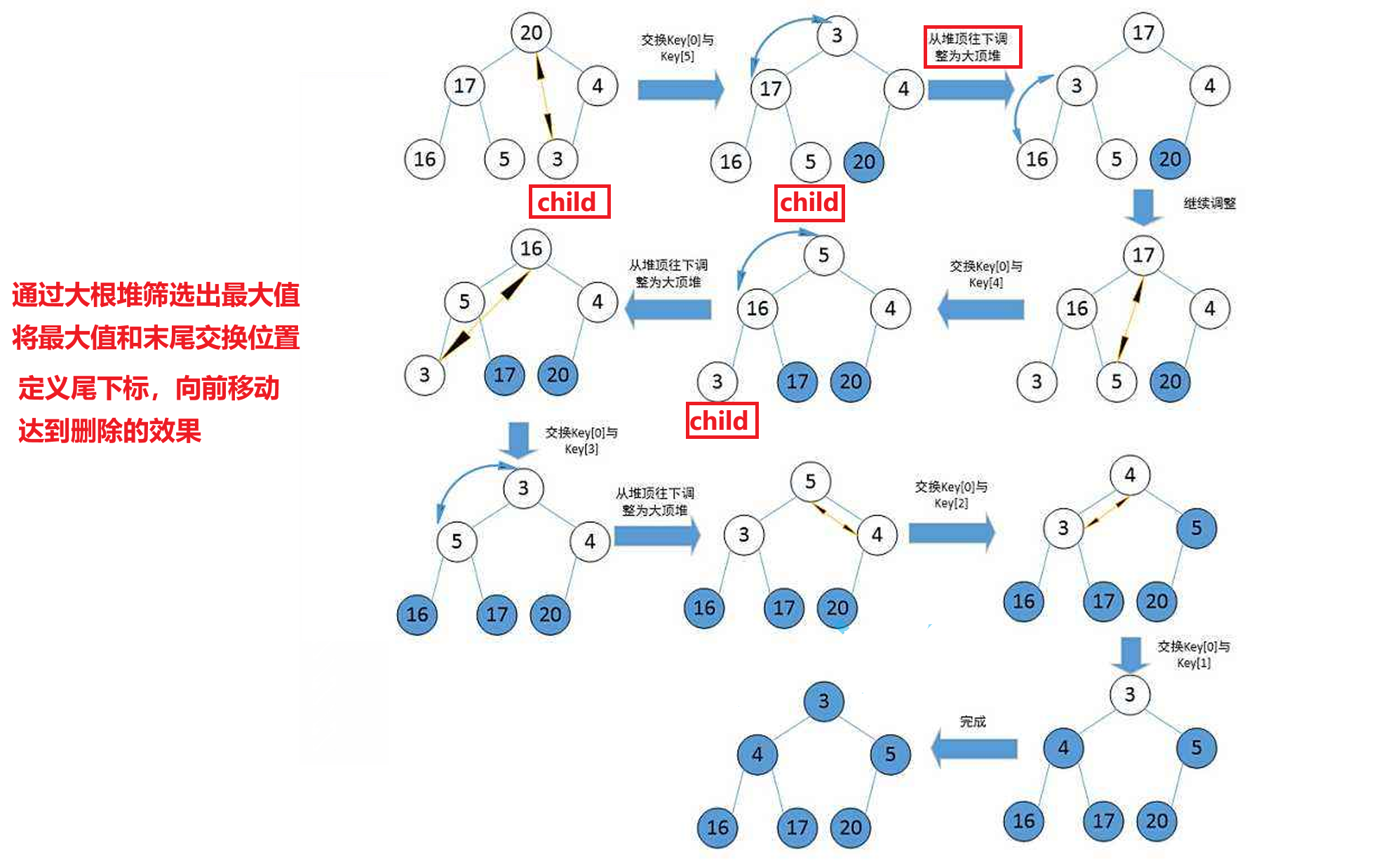
2. 利用堆删除思想来进行排序
举例:
七.PriorityQueue的方法和使用
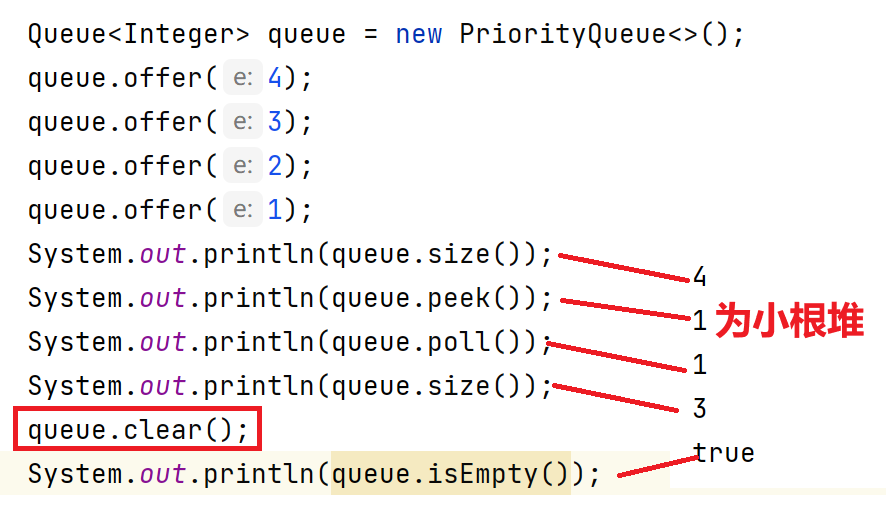
1.方法
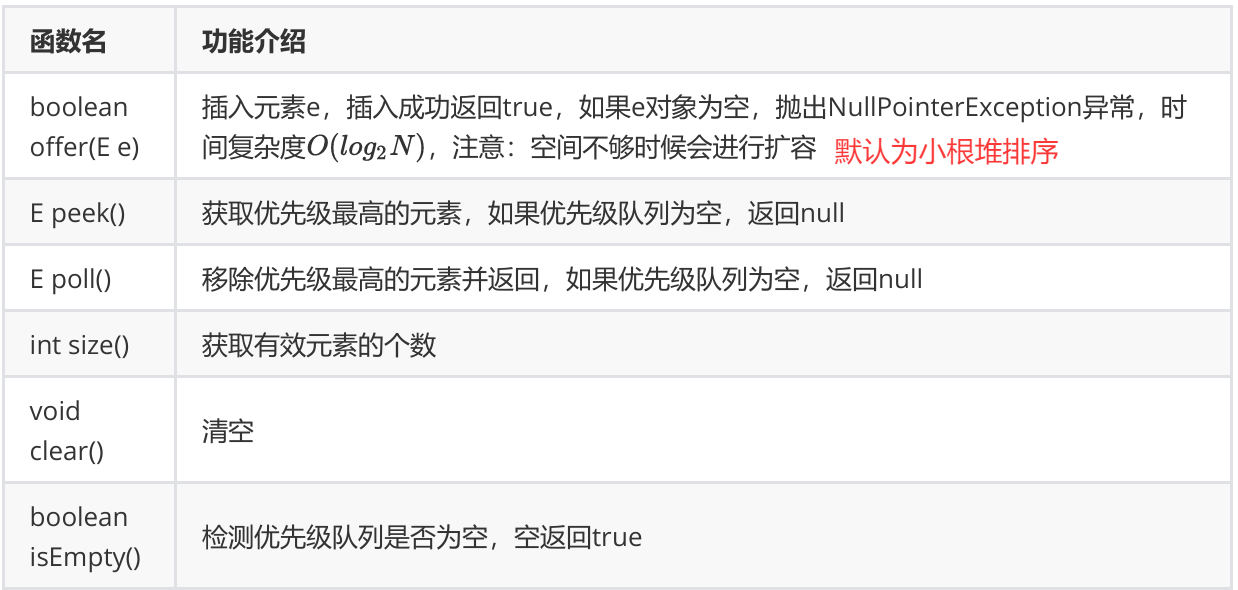
2.使用
3.默认创建为小根堆的原因和如何创造出大根堆
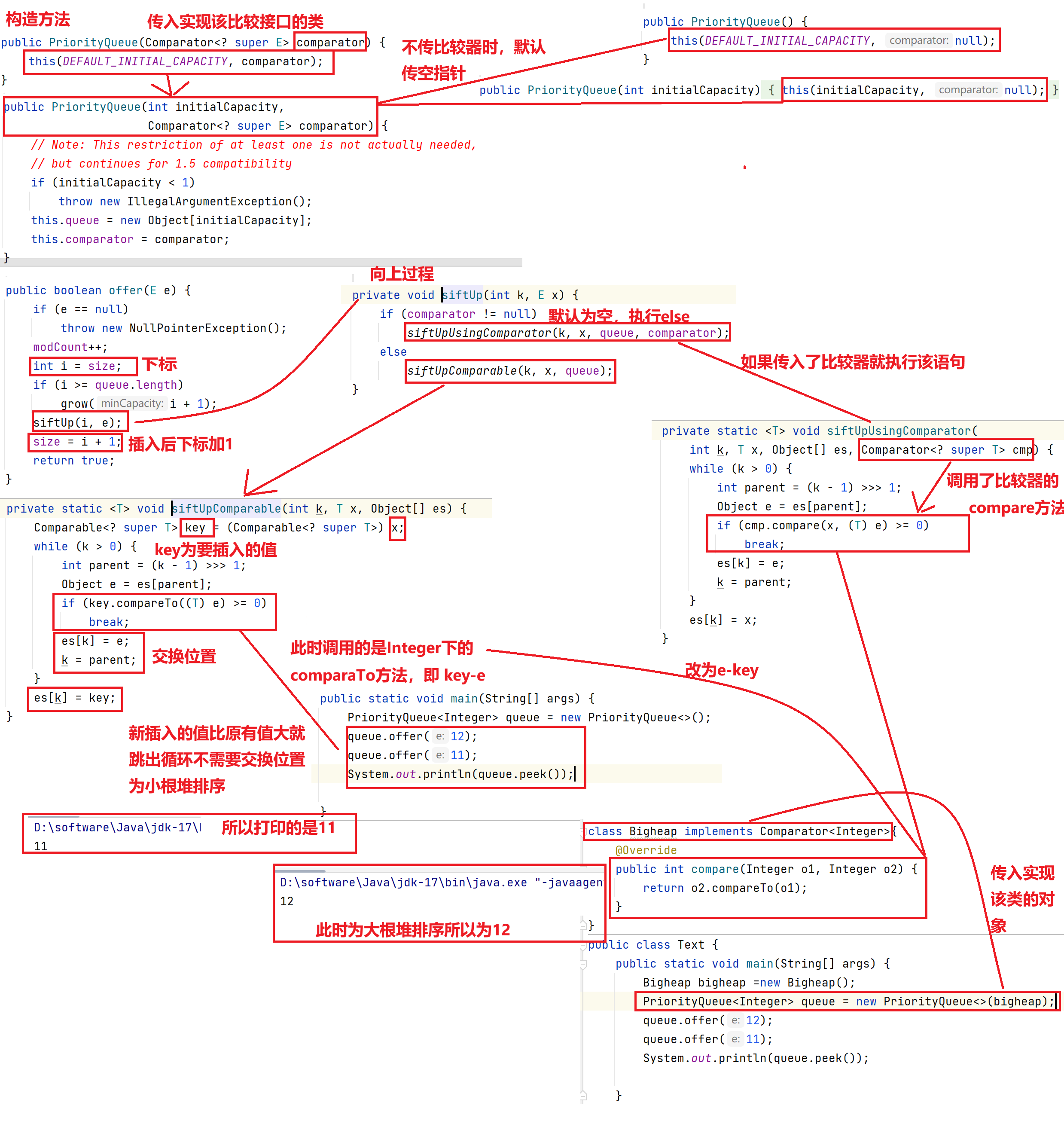
八.Top-K问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
方法1:
public int[] smallestK(int[] arr, int k) {PriorityQueue<Integer> queue = new PriorityQueue<>();for(int i=0;i<arr.length;i++){queue.offer(arr[i]);}int[] ret =new int[k];for(int j=0;j<k;j++){ret[j]=queue.poll();}return ret;}时间复杂度为:
class Bigheap implements Comparator<Integer>{@Overridepublic int compare(Integer o1, Integer o2) {return o2.compareTo(o1);}
}
class Solution {public int[] smallestK(int[] arr, int k) {int[] ret =new int[k];if(arr==null||k==0){return ret;}Bigheap bigheap =new Bigheap();PriorityQueue<Integer> queue = new PriorityQueue<>(bigheap);//klogkfor(int i=0;i<k;i++){queue.offer(arr[i]);}//(N-k)logkfor(int j=k;j<arr.length;j++){int max=queue.peek();if(max>arr[j]){queue.poll();queue.offer(arr[j]);}}//klogkfor(int s =0;s<k;s++){ret[s]=queue.poll();}return ret;}
}时间复杂度为:
同过比较第二种方法好一些。