leetcode112, 257：二叉树的路径总和、二叉树的所有路径双题对比

二叉树路径问题： LeetCode 112 (路径总和) 【难度：简单；通过率：55.5%】和 LeetCode 257 (二叉树的所有路径)【难度：简单；通过率：71.7%】

这两道题都围绕“从根到叶子的路径”展开，是理解 DFS、回溯思想以及递归参数设计的绝佳案例

---

LeetCode 112: 路径总和

一、 题目描述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于 targetSum。如果存在，返回 true；否则，返回 false

示例:

示例 1:

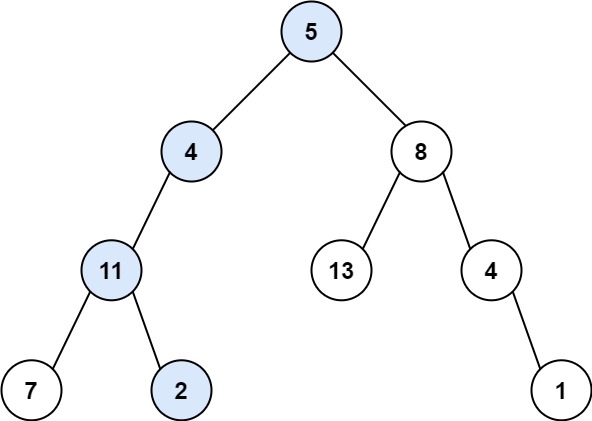
输入: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出: true
解释: 存在路径 5 -> 4 -> 11 -> 2，其和为 22

示例 2:

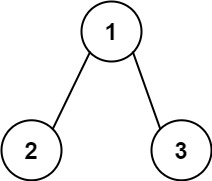
输入: root = [1,2,3], targetSum = 5
输出: false

二、 核心思路与解法分析

目标： 寻找是否存在一条满足条件的路径

思路： 采用深度优先搜索（DFS）。我们从根节点出发，每往下走一步，就将当前路径和累加。当到达一个叶子节点时，检查当前路径和是否等于 targetSum

参考解法

这个解法通过成员变量和巧妙的剪枝，高效地解决了问题

class Solution {int target;boolean isExist = false; // 全局标志，记录是否已找到public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) {return false;}this.target = targetSum;dfs(root, 0);return isExist;}/*** 深度优先搜索* @param node 当前节点* @param sum  从根节点到当前节点父节点的路径和*/public void dfs(TreeNode node, int sum) {// 基准情况：到达叶子节点if (node.left == null && node.right == null) {if (sum + node.val == target) {isExist = true; // 找到路径，设置标志}return; // 无论找没找到，到达叶子节点就返回}// 递归左子树 (隐式回溯)if (node.left != null) {dfs(node.left, sum + node.val);}// 递归右子树，并进行剪枝// 如果左子树已经找到了路径，就没必要再搜索右子树了if (node.right != null && !isExist) {dfs(node.right, sum + node.val);}}
}

关键点解析:

1. 隐式回溯：sum 是 int 类型，按值传递。dfs(node.left, sum + node.val) 调用返回后，当前栈帧的 sum 值不变，天然地完成了“回溯”
2. 剪枝：!isExist 的判断非常关键。一旦找到一条路径，后续的所有递归分支都可以被跳过，大大提高了效率

---

LeetCode 257: 二叉树的所有路径

一、 题目描述

给你一个二叉树的根节点 root，按 任意顺序 返回所有从根节点到叶子节点的路径

示例:

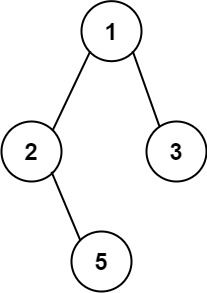
输入: root = [1,2,3,null,5]
输出: [“1->2->5”, “1->3”]

二、 核心思路与解法分析

目标： 寻找并记录所有满足条件的路径

思路： 同样采用深度优先搜索（DFS）。但这次我们不仅要累加和，还要记录下路径本身。当到达叶子节点时，将记录好的路径格式化为字符串并存入结果列表

参考解法 (标准回溯解法)

由于需要记录路径，我们必须在递归时维护一个路径列表，并在回溯时手动将其恢复原状

class Solution {public List<String> binaryTreePaths(TreeNode root) {List<String> result = new ArrayList<>();if (root == null) {return result;}List<Integer> path = new ArrayList<>();dfs(root, path, result);return result;}/*** 深度优先搜索* @param node   当前节点* @param path   记录从根到当前节点的路径节点值* @param result 存储最终结果*/public void dfs(TreeNode node, List<Integer> path, List<String> result) {// 1. 将当前节点加入路径path.add(node.val);// 2. 判断是否到达叶子节点if (node.left == null && node.right == null) {// 到达叶子节点，构建路径字符串并加入结果集StringBuilder sb = new StringBuilder();for (int i = 0; i < path.size() - 1; i++) {sb.append(path.get(i)).append("->");}sb.append(path.get(path.size() - 1));result.add(sb.toString());// 注意：这里不能直接 return，因为后面还有回溯操作}// 3. 递归探索子节点if (node.left != null) {dfs(node.left, path, result);}if (node.right != null) {dfs(node.right, path, result);}// 4. 显式回溯：// 离开当前节点前，将它从路径中移除，以便其他分支使用干净的 pathpath.remove(path.size() - 1);}
}

关键点解析:

1. 显式回溯：path 是 List 类型，按引用传递。所有递归分支共享同一个 path 对象。因此，当一个节点的子树探索完毕，准备返回父节点时，必须通过 path.remove(...) 手动将当前节点从路径中移除，这便是“显式回溯”
2. 不可剪枝：因为题目要求找到“所有”路径，所以即使找到了第一条，也必须继续探索其他所有分支

---

三、 核心对比与总结

特性	LeetCode 112 (路径总和)	LeetCode 257 (二叉树的所有路径)
问题目标	判断存在性 (返回 boolean)	记录所有解 (返回 List<String>)
遍历方式	深度优先搜索 (DFS)	深度优先搜索 (DFS)
回溯方式	隐式回溯 (Implicit Backtracking) - 传递基本类型 int，按值传递，递归返回后自动恢复。	显式回溯 (Explicit Backtracking) - 传递引用类型 List，必须手动 remove 恢复状态。
剪枝	可以剪枝 - 找到一个解后即可停止搜索。	不可剪枝 - 必须遍历整棵树找到所有解。
参数设计	dfs(node, currentSum)	dfs(node, currentPath, resultList)
核心逻辑	在叶子节点判断 sum == target	在叶子节点构建并保存路径字符串

总结：

通过对比这两道题，我们可以深刻理解回溯思想的两种实现方式：

• 当递归只需要传递数值（如 int, double）这类基本数据类型时，通常是隐式回溯
• 当需要维护一个集合（如 List, Set, StringBuilder）这类引用数据类型来记录路径或状态时，就必须进行显式回溯，在递归返回前手动恢复状态