【leetGPU】1. Vector Addition
问题
link: https://leetgpu.com/challenges/vector-addition
Implement a program that performs element-wise addition of two vectors containing 32-bit floating point numbers on a GPU. The program should take two input vectors of equal length and produce a single output vector containing their sum.
Implementation Requirements
External libraries are not permitted
The solve function signature must remain unchanged
The final result must be stored in vector C
解决思路
CUDA使用了SIMT的方法来分配不同线程,也就是对于每个细分后的thread,指令都不一样。这就要我们首先要给并行的函数确定一下他们自己在GPU的什么位置。即要确定thread、block的数量。 对此有如下基础知识:
- thread: 一个CUDA的并行程序会被以许多个thread来执行。
- block: 数个thread会被群组成一个block,同一个block中的thread可以同步,也可以通过shared memory进行通信。
- grid: 多个block则会再构成grid。
解释一下(来源于: https://zhuanlan.zhihu.com/p/123170285):
一个CUDA core可以执行一个thread,一个SM的CUDA core会分成几个warp(即CUDA core在SM中分组),由warp scheduler负责调度。尽管warp中的线程从同一程序地址,但可能具有不同的行为,比如分支结构,因为GPU规定warp中所有线程在同一周期执行相同的指令,warp发散会导致性能下降。一个SM同时并发的warp是有限的,因为资源限制,SM要为每个线程块分配共享内存,而也要为每个线程束中的线程分配独立的寄存器,所以SM的配置会影响其所支持的线程块和warp并发数量。
一个warp中的线程必然在同一个block中, 如果block所含线程数目不是warp大小的整数倍,那么多出的那些thread所在的warp中,会剩余一些inactive的thread,也就是说,即使凑不够warp整数倍的thread,硬件也会为warp凑足,只不过那些thread是inactive状态,需要注意的是,即使这部分thread是inactive的,也会消耗SM资源。 由于warp的大小一般为32,所以block所含的thread的大小一般要设置为32的倍数。
由于一个warp (warp(线程束)是最基本的执行单元) 包含32个并行thread,所以thread的数量应该设置成32的整数倍,一般为256。线程块大小需平衡并行效率和资源限制(如寄存器、共享内存等),一般设置为 threadsPerBlock = 256 每个线程块包含256个线程。
CUDA的软硬件:
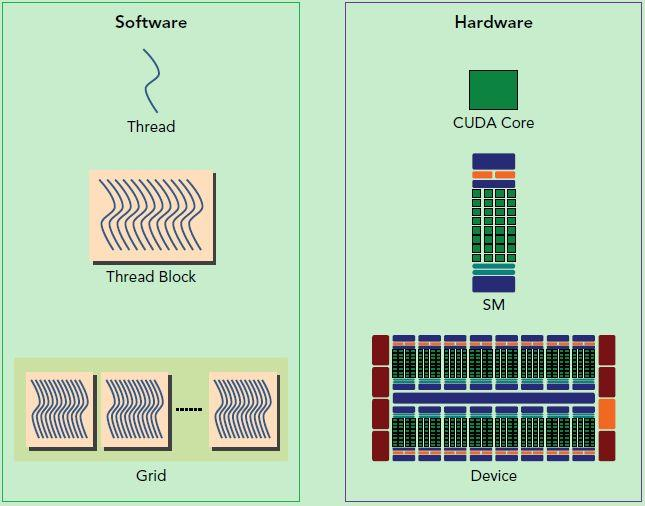
CUDA的软件划分。
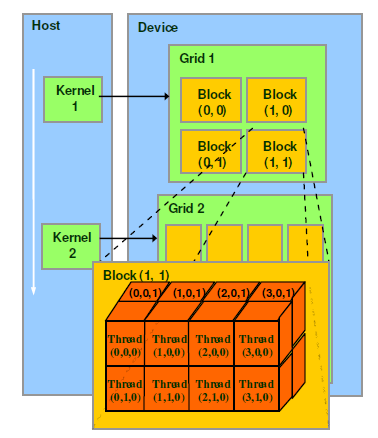
每个grid的block数量可以由下面的公式计算获得.
int blocksPerGrid = (N + threadsPerBlock - 1) / threadsPerBlock;
该公式通过向上取整确保所有 N个元素都有对应的线程处理:
- 分子部分:N + threadsPerBlock - 1通过添加 threadsPerBlock - 1实现向上取整。
- 分母部分:除以 threadsPerBlock得到所需的线程块数量
声明函数
vector_add<<<blocksPerGrid, threadsPerBlock>>>(A, B, C, N);
由于是单一维度的vector,所以只需要用到blockIdx、blockDim和threadIdx的第一维度(x)。后面的二维问题再说y维度。CUDA中每一个线程都有一个唯一的标识ID即threadIdx,这个ID随着Grid和Block的划分方式的不同而变化:
int idx=blockIdx.x*blockDim.x+threadIdx.x;
答案
__global__ void vector_add(const float* A, const float* B, float* C, int N) {int idx=blockIdx.x*blockDim.x+threadIdx.x;if (idx < N) {C[idx] = A[idx] + B[idx]; // 逐元素相加}
}
