当前位置：首页 > news >正文

树上倍增和LCA问题

news 2025/7/27 7:24:07

最近公共祖先问题

一个在图论，尤其是树形结构问题中，几乎是绕不开的核心概念—— 最近公共祖先 (Lowest Common Ancestor, LCA) 。

别小看这个概念，它看似简单，但在解决各种树上查询、路径分析等问题时威力无穷。掌握它，不仅能让你在面对模板题时游刃有余，更能为你打开分析复杂树形问题的思路。很多时候，一个看似棘手的树上问题，其突破口往往就藏在LCA的巧妙运用之中。

让我们从LCA的基本概念出发，逐步深入到高效的求解算法，包括经典的 倍增法 (Binary Lifting) 和基于 欧拉序+RMQ (Range Minimum Query) 的方法。我们不仅要理解算法是怎么做的，更要搞清楚它为什么能这么做，以及在实战中如何灵活运用，如何规避那些常见的“坑”。

什么是最近公共祖先

对于一个有根树，我们引入一个概念：最近公共祖先。对于两个结点 u,vu,v ，如果 xx 满足 xx 是 uu 的祖先，同时也是 vv 的祖先，并且 xx 是满足前述条件中，深度最深的结点，那么我们称 xx 为 u,vu,v 的 最近公共祖先 ，简写为 LCA 。（注意：这里一个结点也被认为是它自己的祖先）。

解决 LCA 问题，对树的路径相关的任何问题都有帮助，这是因为对于树上从 uu 到 vv 的最短路径必然经过最近公共祖先，我们可以将 u,vu,v 的最短路径拆分为 uu 到 LCA 的路径，再从 LCA 到 vv 的路径。

两个结点的 LCA 只有三种可能：

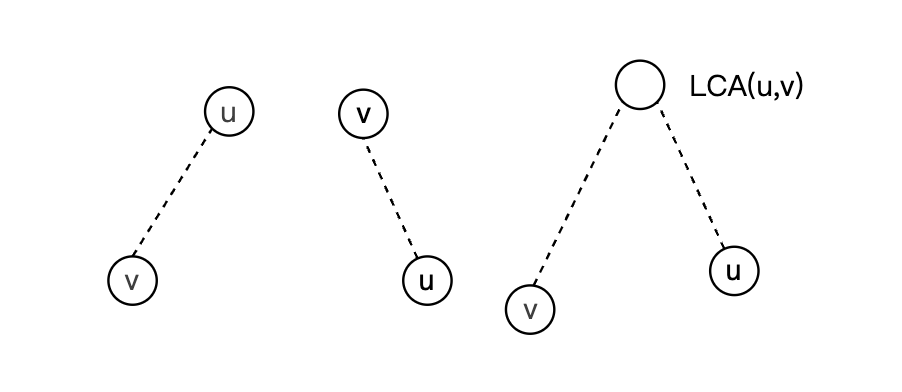
LCA 具有以下性质：

为了方便，我们记点集 S=v1,v2,…,vnS=v1,v2,…,vn 的最近公共祖先为 LCA(v1,v2,…,vn)LCA(v1,v2,…,vn) 或 LCA(S)LCA(S) 。

LCA(u)=uLCA(u)=u ；
uu 是 vv 的祖先，当且仅当 LCA(u,v)=uLCA(u,v)=u ；
如果 uu 不为 vv 的祖先并且 vv 不为 uu 的祖先，那么 u,vu,v 分别处于 LCA(u,v)LCA(u,v) 的两棵不同子树中；
前序遍历中， LCA(S)LCA(S) 出现在所有 SS 中元素之前，后序遍历中 LCA(S)LCA(S) 则出现在所有 SS 中元素之后；
dis(u,v)=h(u)+h(v)−2h(LCA(u,v))dis(u,v)=h(u)+h(v)−2h(LCA(u,v)) ，其中 disdis 是树上两点间的距离， hh 代表某点到树根的距离。
两点集并集的最近公共祖先为两点集分别的最近公共祖先的最近公共祖先，即 LCA(A∪B)=LCA(LCA(A),LCA(B))LCA(A∪B)=LCA(LCA(A),LCA(B)) ；

LCA 之所以重要，是因为它是解决许多树上问题的基础组件。掌握了高效求解LCA的方法，以下这些经典问题往往就能迎刃而解：

树上两点距离 ：结点 uu 和 vv 之间的距离，即它们之间简单路径的边数（或权值和），可以通过它们的深度和它们 LCA 的深度来计算。设 d(x)d(x) 表示结点 xx 的深度（根结点深度通常设为 00 或 11 ）， l=LCA(u,v)l=LCA(u,v) ，则 uu 到 vv 的距离为：
dis(u,v)=dep(u)+dep(v)−2×dep(l)dis(u,v)=dep(u)+dep(v)−2×dep(l)
这个公式非常基础且常用，务必牢记。想一想，从 uu 走到 ll ，再从 ll 走到 vv ，路径长度是 dep(u)−dep(l)+dep(v)−dep(l)dep(u)−dep(l)+dep(v)−dep(l) ，正好是上式。
树上路径查询/修改 ：对于涉及 uu 到 vv 路径上的信息查询（如路径和、路径最大值）或修改（如路径加值），经常需要将路径拆分为 uu 到 LCA(u,v)LCA(u,v) 和 vv 到 LCA(u,v)LCA(u,v) 这两条向上的路径（注意 LCA(u,v)LCA(u,v) 会被计算两次，处理时需小心）。结合树链剖分、树状数组或线段树等数据结构，LCA是定位路径“拐点”的关键。
判断结点间关系 ：判断结点 xx 是否在 uu 到 vv 的路径上？可以检查 LCA(u,x)=xLCA(u,x)=x 或 LCA(v,x)=xLCA(v,x)=x 是否成立，并且 LCA(u,v)LCA(u,v) 是否是 xx 的祖先（或者 xx 就是 LCA(u,v)LCA(u,v) ）。
子树查询与判定 ：虽然 LCA 主要处理祖先关系，但它与子树问题也常常结合。例如，判断一个点是否在另一个点的子树中，可以通过深度和 LCA 关系判断。如果 LCA(u,v)=uLCA(u,v)=u ，则 vv 在 uu 的子树中（或 v=uv=u ）。
构建虚拟树 (Virtual Tree) ：在处理涉及树上 KK 个关键点的问题时，有时我们只需要关心这 KK 个点以及它们两两之间的 LCA 构成的“关键结构”，而不需要整棵树。构建这种只包含关键点和它们 LCA 的“虚拟树”，可以大大降低问题规模。构建虚拟树的第一步，往往就是求解相关结点的 LCA。

可以看到，LCA 的应用场景非常广泛。一个稳定高效的 LCA 算法，是我们在树形结构题目中斩获高分的利器。那么，如何高效地求解 LCA 呢？

LCA问题有 4 种求解的方法，分别有不同的适用范围，接下来我们将重点讲其中的 3 种方法。

朴素算法：一步一步向上爬，直至相遇

可以每次找深度比较大的那个点，让它向上跳。显然在树上，这两个点最后一定会相遇，相遇的位置就是想要求的 LCA。

或者先向上调整深度较大的点，令他们深度相同，然后再共同向上跳转，最后也一定会相遇。

朴素算法 预处理 时需要 dfs 整棵树以计算出结点高度，时间复杂度为 O(n)O(n) ， 单次查询 时间复杂度为 O(n)O(n) 。但由于随机树高为 O(log⁡n)O(logn) ，所以朴素算法在随机树上的单次查询时间复杂度为 O(log⁡n)O(logn) 。

参考代码：

int n, m, s, x, y, fa[N], d[N];
vector<int> g[N];  // 邻接表存（无根）树
// 求每个结点的深度和 fa
void dfs(int u, int f) {fa[u] = f;d[u] = d[f] + 1;for(auto v : g[u]) {if(v != f)dfs(v, u);}
}
// 方法一、每次让深度更大的结点往上跳
int lca(int u, int v) {while(u!=v) {if(d[u] > d[v]) u = fa[u];else v = fa[v];}return u;
} 
// 方法二、先向上调整深度较大的点，令他们深度相同，然后再共同向上跳转
int lca(int u, int v) {// 把 u 移动到和 v 同一高度if(d[u] < d[v]) swap(u, v);while(d[u] > d[v]) u=fa[u];// 开始同步往上跳while(u!=v) {u = fa[u];v = fa[v];}return u;
} 
dfs(s, 0);  // 或者 dfs(s, s) 从根出发，预处理出 fa 和 d 数组

采用朴素算法求 LCA 的时间复杂度与两点间的距离有关，极限情况可达到 O(n)O(n) 。虽然该算法时间复杂度较高，但该算法也是有一定的应用价值的：

它实现简单，可在算法竞赛中快速和正确的程序对拍。
随机产生的树的高度期望是 O(log⁡n)O(logn) 级别的，有些时候树是随机的或者树的深度不大，我们也可以使用该算法。
这个算法允许树动态改变。我们只需要知道每个点的父结点和深度，就可以方便地求出两个点的 LCA（当然如果更进一步地我们不知道点的深度，也可以先从一个点走到根，把路径上的点都标记了，再从另一个点向根走，走到标记的点为止）。另一个可以处理动态情况的数据结构是 动态树 ，但它实现复杂而且常数因子较大。所以在这个特定情况下，该算法具有不可替代的作用。

除了往上一步一步爬以外，我们也可以使用另一种朴素的方式来得到 LCA——标记祖先路径：

任选一点向上标记 ：选择 uu 或 vv 中的一个（比如 uu ），从 uu 开始不断向上走到根结点，沿途标记所有经过的结点。
另一点向上查找 ：从另一个结点v开始，不断向上走到根结点。
首次遇到的标记点 ：在v向上走的过程中，遇到的第一个被标记过的结点，就是 LCA(u,v)LCA(u,v) 。

容易知道，这样的方法的时间复杂度也是 O(n)O(n) 的。

上面这两种朴素方法虽然简单直观，但效率瓶颈在于“ 一步一步向上爬 ”。这启发我们思考：能不能一次跳跃多步？

倍增算法：一次跳 2k2k 步

本算法是对朴素算法中一步一步向上爬的改进，核心思想是让两个结点 每次向上走 22 的幂次步 ，具体操作如下：

Step 1. 预处理出倍增数组：

首先开一个 n×log⁡nn×logn 的数组，比如 fa[n][log⁡n]fa[n][logn] ，其中 fa[u][i]fa[u][i] 表示 uu 结点的第 2i2i 个父亲 。 fa[u][i]fa[u][i] 为结点 uu 向上走 2i2i 步后能走到的结点。我们规定根结点的父亲是它自己，这样根结点往上走还是在根结点（设为一个不存在的结点，比如 00 也是可以的）。

对于 i=0i=0 ， fa[u][i]fa[u][i] 就是结点 uu 的父亲。
对于 i>0i>0 ，类似于序列上的倍增， fa[u][i]fa[u][i] 等于 fa[fa[u][i−1]][i−1]fa[fa[u][i−1]][i−1] （即结点 uu 往上走 2i−12i−1 步后再往上走 2i−12i−1 步)。

我们可以通过一遍从根结点开始的 dfs 预处理出 fafa 数组和深度数组 dd 。

vector<int> g[N]; // 邻接表存树
int d[N], fa[N][lg]; // dep 存深度, fa[x][k] 存 x 的 2^k 祖先
int lg[N]; // 预处理 log2(i)
void dfs(int u, int f) {fa[u][0] = f;  d[u] = d[f]+1;// 倍增法计算 u 的第 2^i 个父结点 = u 的第 2^{i-1} 个祖先的第 2^{i-1} 个祖先for(int i = 1; i <= lg[d[u]]; i++)  // 注意枚举的上界，上界也可以写成：(1<<i) <= d[u]fa[u][i] = fa[fa[u][i-1]][i-1];   // 倍增递推// 如果 fa[u][i-1] 是根结点 (假设根的父结点是0)// 那么 fa[u][i] 也应该是 0// 这里假设 fa[0][i-1] = 0, 所以不需要特殊处理for(int v : g[u]) {if(v != f) dfs(v, u);}
}

Copy

Step 2. 把两个点移到同一深度：

以要求 LCA(u,v)LCA(u,v) 为例。

假设 d[u]≥d[v]d[u]≥d[v] （如果不满足，那么交换 u,vu,v ）这样就能保证 uu 深度大于等于 vv 深度
类似于暴力跳，我们需要让 uu 往上跳 d[u]−d[v]d[u]−d[v] 步，这样跳完之后， u,vu,v 的深度就相同了。
我们对这个深度差进行 二进制拆分 ，就可以通过倍增数组往上走 22 的最大的幂次步（即 log⁡2(d[u]−d[v])log2(d[u]−d[v]) ，更新 u=fa[u][i]u=fa[u][i] ），那么可以在 O(log⁡2n)O(log2n) 的时间复杂度内到达目标深度。或者，我们也可以从大往小扫描 ii ，一直尝试到 00 （包括 00 ），如果每次 fa[u][i]fa[u][i] 深度不小于 vv ，我们就跳 u=fa[u][i]u=fa[u][i] 。两种做法效果是一样的，读者可以根据自己的喜好选择。

if(d[u] < d[v]) swap(u, v);
// 方法一、倍增跳
while(d[u] > d[v]) u=fa[u][lg[d[u]-d[v]]];
// 方法二、枚举数位跳
for(int i = lg[d[u]]; i >= 0; i--) {if(d[fa[u][i]] >= d[v]) // 如果跳 2^i 步后还比 v 深或刚好，那就跳u = fa[u][i];
}

这一步结束后， d[u]=d[v]d[u]=d[v] 必然成立。

Step 3. 求出 LCA：

如果此时 u=vu=v ，那么 uu 就是要求的 LCA。这也说明原本要求的 u,vu,v 结点中 u,vu,v 两个结点中，有一个是另一个的祖先。

否则 u≠vu=v ，那么则让 uu 和 vv 同时向上跳，直到 u,vu,v 的父结点相同：

再次利用 倍增数组和二进制拆分 ，从大到小枚举跳 2i2i 步， ii 从 log⁡2d[u]log2d[u] 枚举到 00 。
如果 fa[u][i]≠fa[v][i]fa[u][i]=fa[v][i] ，说明它们向上跳 2i2i 步后，还没有到达 LCA，就往上跳 2i2i 步， u=fa[u][i],v=fa[v][i]u=fa[u][i],v=fa[v][i] 。
如果 fa[u][i]=fa[v][i]fa[u][i]=fa[v][i] ，说明它们向上跳 2i2i 步后，可能到达了 LCA，但也有可能跳过了 LCA。此时我们不能往上跳。

if(u == v) return u;
// 开始同步往上跳 2^i 步
for(int i = lg[d[u]]; ~i; i--) {// 只要往上跳 2^i 步父结点还不相同，就继续上跳if(fa[u][i] != fa[v][i])u = fa[u][i], v = fa[v][i]; 
}
return fa[u][0];   // 第一个父结点就是 LCA

为什么得到的是同一个结点我们不跳，得到的是不同结点反而需要跳？

这是因为我们无法确定这个相同的祖先结点是不是 LCA。如果不是 LCA，我们更无法确定接下来往回跳多少。

查询复杂度：

Step 1 (对齐深度)：循环次数是 O(log⁡n)O(logn) ，每次操作 O(1)O(1) 。复杂度 O(log⁡n)O(logn) 。
Step 2 (判断相等)： O(1)O(1) 。
Step 3 (同步跳跃)：循环次数是 O(log⁡n)O(logn) ，每次操作 O(1)O(1) 。复杂度 O(log⁡n)O(logn) 。
单次查询总时间复杂度： O(log⁡n)O(logn) 。

整体复杂度：

预处理： O(nlog⁡n)O(nlogn) 时间， O(nlog⁡n)O(nlogn) 空间。
查询： O(log⁡n)O(logn) 时间。

对于 n,Q≤105∼106n,Q≤105∼106 的规模，这个复杂度是非常优秀的，足以通过绝大多数竞赛题目。

另外，值得一提的是倍增算法可以通过交换 fa 数组的两维使较小维放在前面。这样可以减少 cache miss 次数，提高程序效率。

我们来实现一个解决标准 LCA 问题的模板：P4070 - 最近公共祖先。

题意概括: 给定一棵 nn 个结点的有根树，根为 ss ，以及 mm 次询问，每次询问给出两个结点，求它们的最近公共祖先。

参考代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n, m, s, x, y, fa[N][20], d[N], lg[N];
vector<int> g[N];
// 求每个结点的深度和 fa[][]
void dfs(int u, int f) {fa[u][0] = f;  d[u] = d[f]+1;// 二分法计算 u 的第 2^i 个父结点// 是 u 的第 2^{i-1} 个祖先的第 2^{i-1} 个祖先for(int i = 1; i <= lg[d[u]]; i++)fa[u][i] = fa[fa[u][i-1]][i-1];for(int v : g[u]) {if(v != f) dfs(v, u);}
}
// 先向上调整深度较大的点，令他们深度相同，然后再共同向上跳转
int query(int u, int v) {// 把 u 移动到和 v 同一高度if(d[u] < d[v]) swap(u, v);while(d[u] > d[v]) u=fa[u][lg[d[u]-d[v]]];if(u == v) return u;// 开始同步往上跳 2^i 步for(int i = lg[d[u]]; ~i; i--) {// 只要往上跳 2^i 步父结点还不相同，就继续上跳if(fa[u][i] != fa[v][i])u = fa[u][i], v = fa[v][i]; }return fa[u][0];   // 第一个父结点就是 LCA
} 
int main() {cin >> n >> m >> s;for(int i = 1; i < n; i++) {cin >> x >> y;g[x].push_back(y);g[y].push_back(x);}// 预处理 log_2 数组 lg[i]for(int i = 2; i <= n; i++) lg[i] = lg[i/2] + 1;// dfs 预处理获取深度和 fa 数组dfs(s, 0);  // 这里认为根结点的父结点是 0for(int i = 1; i <= m; i++) {cin >> x >> y;cout << query(x, y) << '\n';}return 0;
}

Copy

倍增法是求解 LCA 问题最常用、最稳定的方法之一，代码相对直观，效率也足够应对大多数场景。建议同学们一定要熟练掌握其原理和实现。

现在，我们已经掌握了一种 O(nlog⁡n)O(nlogn) 预处理、 O(nlog⁡n)O(nlogn) 查询的LCA算法。有没有更快的方法呢？特别是在查询次数极多 ( mm 远大于 nn ) 的情况下，我们可能希望查询复杂度能达到 O(1)O(1) 。这就要引出另一种强大的思路： 将树问题转化为序列问题 。

欧拉序列转 RMQ 问题：树变序列， O(1)O(1) 查询

1. 欧拉序列和 LCA

欧拉遍历指的是在 DFS 过程中，不仅在进入一个结点时记录它，在回溯离开一个结点（即访问完其所有子树后）时也记录它。或者，进入结点时记录当前结点，从每个子结点返回时也记录当前结点。

这里我们采用后一种方案，也是更常用于 LCA 的记录方式： 进入结点时记录，从结点回溯时也记录父结点。 这样，我们可以得到一个长度为 2n−12n−1 的序列，这个序列被称作这棵树的 欧拉序列 。（思考：这么记录的话，有的结点可能会被记录不止两次，那为什么序列长度却一定是 2n−12n−1 ？）

例如，下图中的树的欧拉序列为： 1,2,5,2,6,9,6,2,1,3,7,3,1,4,8,4,11,2,5,2,6,9,6,2,1,3,7,3,1,4,8,4,1 。

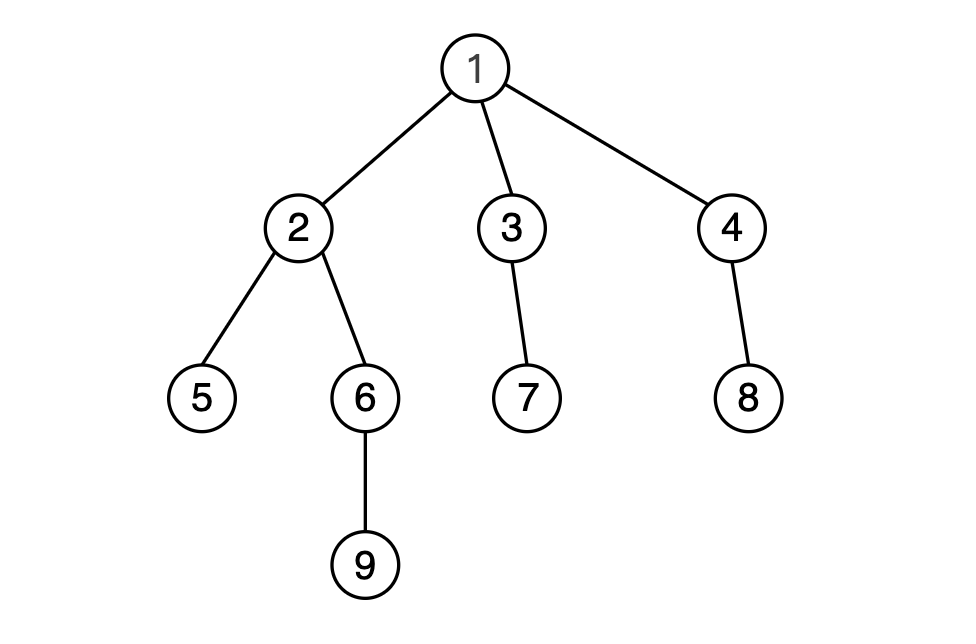
为了方便，我们把结点 uu 在欧拉序列中第一次出现的位置编号记为 first(u)first(u) （也称作结点 uu 的 欧拉序 ），把欧拉序列本身记作序列 seq[1∼2n−1]seq[1∼2n−1] 。

同步地，我们记录欧拉序列中每个结点的深度。对于上图中的例子，我们具体会得到如下序列信息：

seq[]seq[] ： [1,2,5,2,6,9,6,2,1,3,7,3,1,4,8,4,1][1,2,5,2,6,9,6,2,1,3,7,3,1,4,8,4,1] ，长度为 2n−12n−1 。
dep[]dep[] ： [1,2,3,2,3,4,3,2,1,2,3,2,1,2,3,2,1][1,2,3,2,3,4,3,2,1,2,3,2,1,2,3,2,1] ，对应 seqseq 中每个结点的深度。
first[]first[] ： [1,2,10,14,3,5,11,15,6][1,2,10,14,3,5,11,15,6] ，结点首次出现的位置，索引（下标）从 11 开始。

int seq[N<<1];  // 欧拉序列
int dep[N<<1];  // dep[i]: 欧拉序列中第 i 个结点的深度
int first[N], len; // first[i]：结点 i 第一次遍历到的位置
vector<int> g[N];  // 邻接表存树
// dfs 求欧拉序列、对应的深度序列和 每个结点第一个出现的位置
void dfs(int u, int f, int d) {seq[++len] = u; dep[len] = d; first[u] = len;for(int v : g[u]) {if(v == f) continue;dfs(v, u, d + 1);seq[++len] = u; dep[len] = d;}
}

有了欧拉序列，LCA 问题可以在线性时间内转化为 RMQ 问题：结点 uu 和 vv 的最近公共祖先 LCA(u,v)LCA(u,v) ，就是欧拉序列 seqseq 中，在 uu 第一次出现的位置 first[u]first[u] 和 vv 第一次出现的位置 first[v]first[v] 之间的那段子区间中，深度 depdep 最小的那个结点（假设 first[u]≤first[v]first[u]≤first[v] ）。即

first(LCA(u,v))=min⁡{first(k)∣k∈seq[first(u)..first(v)]}first(LCA(u,v))=min{first(k)∣k∈seq[first(u)..first(v)]}

这个结论不难理解： 从 uu 走到 vv 的过程中一定会经过 LCA(u,v)LCA(u,v) ，但不会经过 LCA(u,v)LCA(u,v) 的祖先 。因此，从 uu 走到 vv 的过程中经过的欧拉序最小的结点就是 LCA(u,v)LCA(u,v) 。

2. 用欧拉序和ST表求解LCA问题

有了上面的结论，现在问题就转化为：如何快速查询一个序列（这里是 firstfirst 序列）在给定的区间 [first(u),first(v)][first(u),first(v)] 内的最小值，以及其对应的原始结点（在 seqseq 欧拉序列中的值）。

这正是经典的 RMQ 问题，对于静态的序列，可以使用 ST 表高效解决。

用 DFS 计算欧拉序列的时间复杂度是 O(n)O(n) ，且欧拉序列的长度也是 O(n)O(n) ，所以 LCA 问题可以在 O(n)O(n) 的时间内转化成等规模的 RMQ 问题。

仍旧针对上面的模板问题，我们给出一份参考代码实现。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n, m, s, x, y, st[N<<1][20];  // st[i][j]: 欧拉序列中第 i~j 个结点中的深度最小的结点的编号
int lg[N<<1]; // lg[i]: 比 i 小的最大的 2次幂数
// seq[i]：欧拉序列, dep[i]: 欧拉序列中第 i 个结点的深度， first[i]: 结点 i 第一次遍历到的位置
int seq[N<<1], dep[N<<1], first[N], len;
vector<int> g[N];  // 邻接表存树
// dfs 求欧拉序列、对应的深度序列和 每个结点第一个出现的位置
void dfs(int u, int f) {seq[++len] = u; dep[len] = d; first[u] = len;for(int v : g[u]) {if(v == f) continue;dfs(v, u, d + 1);seq[++len] = u; dep[len] = d;}
}void init(int root) {dfs(root, 0, 1);for(int i = 2; i <= len; i++)lg[i] = lg[i/2] + 1;// ST 表预处理for(int i = 1; i <= len; i++) st[i][0] = i;for(int j = 1; (1<<j) <= len; j++)for(int i = 1; i+(1<<j)-1<=len; i++) {int p1 = st[i][j-1];int p2 = st[i+(1<<(j-1))][j-1];st[i][j] = (dep[p1] < dep[p2] ? p1 : p2);}
}
int query(int x, int y) {int l = first[x], r = first[y];if(l > r) swap(l, r);int k = lg[r-l+1];int p1 = st[l][k];int p2 = st[r-(1<<k)+1][k];return dep[p1] < dep[p2] ? seq[p1] : seq[p2];  // 注意要转回原结点编号
} int main() {cin >> n >> m >> s;for(int i = 1; i < n; i++) {cin >> x >> y;g[x].push_back(y);g[y].push_back(x);}init(s);for(int i = 1; i <= m; i++) {cin >> x >> y;cout << query(x, y) << '\n';}return 0;
}

代码实现注意事项：

序列长度： 欧拉序列 seq 和对应的结点深度序列 dep 的长度都是 2N−12N−1 的，ST 表和 lg 数组也是类似的。开数组时要确保大小足够。
ST 表存储： st[i][j] 存储的是对应区间内深度最小的结点的索引，在更新和查询时比较要用 dep 数组的值比较。
±1 RMQ优化 (进阶) ：仔细观察 dep 序列，相邻两个元素的深度差一定是 +1+1 或 −1−1 。这种特殊的 RMQ 被称为 ±1 RMQ 。对于 ±1RMQ±1RMQ 问题，存在 O(N)O(N) 时间预处理、 O(1)O(1) 时间查询的算法（如Farach-Colton和Bender的算法）。这意味着 LCA 问题理论上可以做到 O(N)O(N) 预处理、 O(1)O(1) 查询。但在实际竞赛中，由于 O(N)O(N) 算法实现复杂，常数较大，除非 NN 极大且 MM 极大，否则 O(Nlog⁡N)O(NlogN) 预处理、 O(1)O(1) 查询的 ST 表方法通常是更好的选择，也更常用。我们在这里不展开 O(N)O(N) 的 ±1 RMQ 算法，有兴趣的同学可以自行深入研究。

赛场变幻莫测，出题人总会想方设法考验我们对知识的理解深度和广度。接下来，我们将探讨一种非常巧妙的离线算法——Tarjan算法，以及LCA在更复杂场景下的应用，比如动态树和虚拟树构建，最后还会分享一些实战经验和避坑指南。

Tarjan 算法：离线的智慧- DFS与并查集

我们前面介绍过 Tarjan 的贡献，他发明了很多名字叫 Tarjan 的算法。注意，此 Tarjan 算法非彼 Tarjan 算法。

前面介绍的倍增法和欧拉序+ST 表都是在线（Online）算法，意味着它们可以在预处理完成后，随时回答任何一个 LCA 查询，查询之间相互独立。

但有时，题目会一次性给出所有的查询， 允许我们先读入所有查询，再统一处理 。这种场景下，离线（Offline）算法就有了用武之地。Tarjan 的 LCA 算法就是一种基于 DFS 和并查集的经典离线算法。

Tarjan 算法巧妙地在对树进行一次 DFS 的过程中，同时处理所有与当前 DFS 子树相关的查询。它利用并查集来维护 已经访问过并回溯的结点所形成的子树 （或者说，维护结点的“祖先链”信息），并且把每个询问 (x,y)(x,y) 同时存储在结点 xx 和结点 yy 上。从而在递归回溯时找到结点上每个额询问的 LCA。

核心思想：

考虑在树上进行 DFS，从 uu 经过边 (u,v)(u,v) 到子结点 vv 之后，遍历了 vv 所在的子树之后，（类似 Tarjan 求有向图的强连通分量）再从边 (u,v)(u,v) 返回 uu 结点之前，考虑我们能获取什么信息。对于所有询问结点 x=vx=v 和另一个结点 yy 的最近公共祖先， yy 有三种可能：

yy 已经被遍历过了：
- yy 在以 vv 为根的子树上：此时 LCA(v,y)=vLCA(v,y)=v 。
- yy 不在以 vv 为根的子树上：此时 LCA 必然是 yy 的某个祖先，或者就是 yy 自身。
yy 尚未被遍历到：那么如果继续遍历，当遍历到 yy 并从 yy 回溯时， vv 已经被遍历到了（就相当于上面第二种情况），因此，询问 (v,y)(v,y) 我们可以放到 yy 结点考虑并处理。

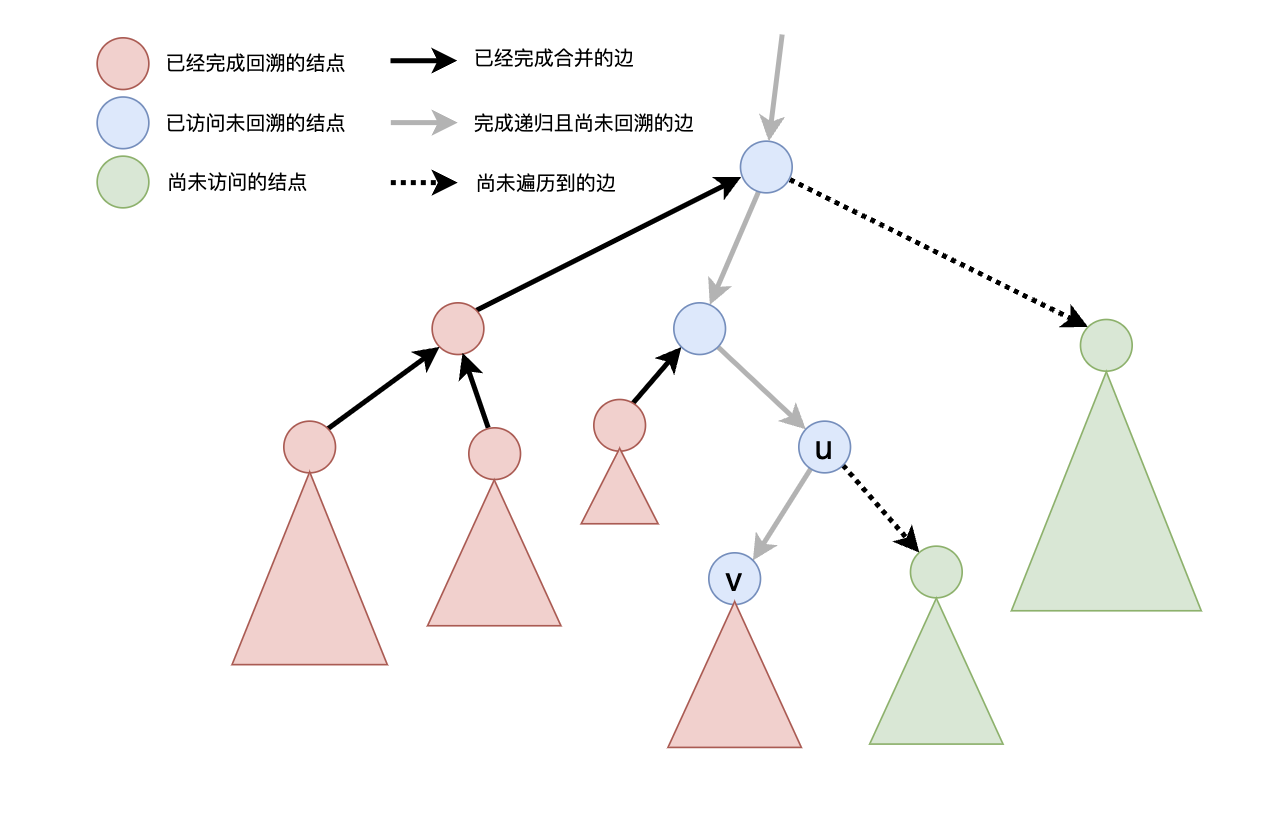
如果我们在 DFS 的同时，用并查集做树上结点的合并：在遍历完 vv 所在的子树，并从子结点 vv 返回后做合并操作 merge(u,v)。由于我们要求 LCA，因此，这里的合并要求是 子结点 vv 合并到 uu 所在的集合上 。对于这样的并查集，可以确定，合并后 u,vu,v 所在集合的代表元指向 vv 的（未完成回溯且深度最深）的祖先结点 。

在 DFS 遍历完 uu 的所有子结点，将子结点集合合并到 uu 结点。从结点 uu 回溯之前，处理询问。那么，对于上面询问（求结点 x=vx=v 和另一个结点 yy 的最近公共祖先）的三种情况，就有如下结论：

yy 已经被遍历过了：询问的答案即为 find(y)。
- yy 在以 vv 为根的子树上：此时 LCA(x=v,y)=xLCA(x=v,y)=x ，由于 yy 结点已经完成了回溯并合并到 xx 结点上，因此 find(y)=x。
- yy 不在以 vv 为根的子树上：此时 LCA 就是结点 yy 所在集合的代表元，即 find(y) 。
yy 尚未被遍历到：无需做处理，当前询问 (x,y)(x,y) 的结果会在遍历到 yy 结点时得到。

为什么 find(y) 就是此时 x,yx,y 的最近公共祖先？

上面我们已经知道，合并操作 merge(u,v) 执行后， u,vu,v 所在集合的代表元现在都指向 vv 的（未完成回溯且深度最深）的祖先结点 。记 s=find(y)s=find(y) ，那么， ss 就是 yy 结点的未完成回溯的深度最深的祖先结点。

注意到，此时 v=xv=x 结点即将进行回溯，也就是说 vv 尚未完成遍历，因此 vv 必然是 ss 的后代， ss 也就是 v=xv=x 的祖先（严格来说，此时所有未完成回溯的结点都是 xx 的祖先，它们构成了一条含有结点 ss 的“祖先链”）。因此， ss 是 x,yx,y 的公共祖先。

又因为 ss 是未完成回溯的深度最深的祖先结点，而 yy 的已完成回溯的祖先结点不可能是 xx 的祖先（ xx 尚未完成回溯），所以 ss 是 x,yx,y 的最近公共祖先。

代码实现：

1. 基本数据结构：

vector<> g[N]：邻接表存树。
fa[N] + find(u,v) + merge(u,v) ：并查集维护结点的祖先信息。
vis[N] 标记数组：结点在 DFS 中是否已被访问并完成回溯。
ans[M] 离线答案数组：存储 MM 个查询的结果。
vector<pair<int, int>> q[N] 或类似结构存储查询：q[u]` 存储所有查询对中包含结点 uu 的查询信息（另一个结点 vv 以及该查询的编号 idid ）。

2. 预处理：

读入树的结构。
读入所有 MM 个查询 (ui,vi)(ui,vi) 。将每个查询 (ui,vi)(ui,vi) 分别挂在结点 uiui 和 vivi 上：向 q[u_i] 中添加 {v_i, i}，向 q[v_i] 中添加 {u_i, i}。
初始化并查集，每个结点自成一个集合：fa[i] = i。
初始化 vis 数组为 false。

3. DFS + 处理查询（`tarjan(u)` ）

标记 u 为“正在访问”（如果需要）。
遍历 u 的子结点 v：
- 如果 v 未被访问过（即 v 不是 u 的父结点），递归调用 tarjan(v)。
- 关键步骤 ：当从子结点v递归返回后，将子树v合并到u中：merge(u, v)。
回溯前处理与u相关的查询：
- 遍历 q[u] 中的每个查询 {v, id}。
- 检查v的状态，如果结点v已经被访问并完成回溯（即 vis[v] 为 true ），那么记录查询的答案：ans[id] = find(v) 。
标记u完成回溯 ：在u的所有子结点都处理完毕，并且与u相关的查询也处理完毕后，标记 vis[u] = true 。

DFS 结束后，ans 数组中就存储了所有查询的结果。

仍旧针对上面的模板问题，我们给出一份参考代码实现。

#include <bits/stdc++.h>
using namespace std;const int N = 5e5+5, M = 5e5+5;
int n, m, s, fa[N], ans[M];
bool vis[N];
vector<int> g[N];
vector<pair<int,int>> q[N];  // 存储查询 {v, id}
int find(int u) {if(u == fa[u]) return u;return fa[u] = find(fa[u]);  // 路径压缩
}
void merge(int u, int v) {u = find(u); v = find(v);fa[v] = u;  // 将 v(子树) 合并到 u(祖先结点)
}
void dfs(int u, int f) {// vis[u] = true; // 标记正在访问 (如果需要区分已访问、正在访问、未访问三种状态)for(int v : g[u]) {if(v != f) {dfs(v, u);merge(u, v);  // 注意：v 往 u 合并}}for(auto& e : q[u]) {  // 回溯前遍历和 u 相关的查询 -> 离线查询int &v = e.first, &id = e.second;if(vis[v] /* ||u==v */) {  // 也可以在这里增加特判 u==v 的情况ans[id] = find(v);}}vis[u] = true;  // 标记 u 访问并回溯完成
}
int main(){cin >> n >> m >> s;for (int i=1,u,v; i < n; i++) {cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}for (int i=1,u,v; i <= m; i++) {  // 查询挂到两个结点上cin >> u >> v;if(u==v) ans[i] = u;  // 如果不特判，上面 L18 行要标记，否则询问答案无法保存else {q[u].push_back({v,i});q[v].push_back({u,i});}}for (int i=1; i <= n; i++) {fa[i] = i;}dfs(s, 0);for (int i=1; i <= m; i++) {  // 输出每个询问的结果cout << ans[i] << '\n';}return 0;
}

代码实现注意事项：

并查集的合并方向： 必须将子结点往父结点合并，否则无法确定祖先是谁。（父结点是子结点的第一个祖先）
u=vu=v 的查询： 可以直接特判处理掉，如果不做任何特判，要注意 vis 标记的处理时机，不特判时，结点递归进入时就可以标记，而不能等到回溯时标记，否则 u=vu=v 的查询就获取不到。

复杂度分析：

预处理读入和存储查询： O(N+M)O(N+M) 。
并查集初始化： O(N)O(N) 。
DFS遍历：每个结点和边访问一次， O(N)O(N) 。
并查集操作：总共 N−1N−1 次 merge 和 O(M)O(M) 次 find 。使用按秩合并或路径压缩优化的并查集，单次操作的平均时间复杂度接近 O(α(N))O(α(N)) ，其中 αα 是反阿克曼函数，增长极其缓慢，可以视为近似常数。总复杂度 O((N+M)α(N))O((N+M)α(N)) 。
总时间复杂度： O(N+M+(N+M)α(N))≈O(N+M)O(N+M+(N+M)α(N))≈O(N+M) （在 α(N)α(N) 近似为常数时）。
空间复杂度： O(N+M)O(N+M) （邻接表、并查集数组、查询存储）。

优点：

时间复杂度几乎是线性的，非常高效，尤其在 MM 很大的时候。
代码实现相对简洁，只需要 DFS 和并查集。

缺点：

必须离线处理，无法应对需要实时回答查询的场景。
需要存储所有查询，空间开销 O(N+M)O(N+M) 可能比在线算法的 O(Nlog⁡N)O(NlogN) 要大（如果 MM 很大的话）。

树链剖分法：树拆为链

上面提到的三种做法，空间消耗均至少为 O(nlog⁡n)O(nlogn) ，如果空间较为紧张，树剖法求解 LCA 会比较适用。

利用树链剖分求解，预处理时间复杂度 O(n)O(n) ，单次查询 O(log⁡⁡n)O(log⁡n) ，属于在线算法。

在介绍树剖法之前，需要先介绍一个概念： 轻重路径剖分 。

对于一个有根树，我们可以定义一个结点的 sizesize 为以这个结点为根的子树的结点个数。

对于每个结点，我们都定义它的 重儿子 为它儿子中 sizesize 最大的那个。定义连接某个结点和它重儿子的边为重边，其余的边称为轻边。容易知道，除叶结点没有重儿子外，每个结点有且仅有有一个重儿子。我们把连续首尾衔接的重边及其所有端点组成的链叫做重链，特别地， 落单的结点也当作重链 。

我们用 粗黑色 表示重边， 细黑色 表示轻边，那么对于下面这棵树，它的结果是这样的：

HLD

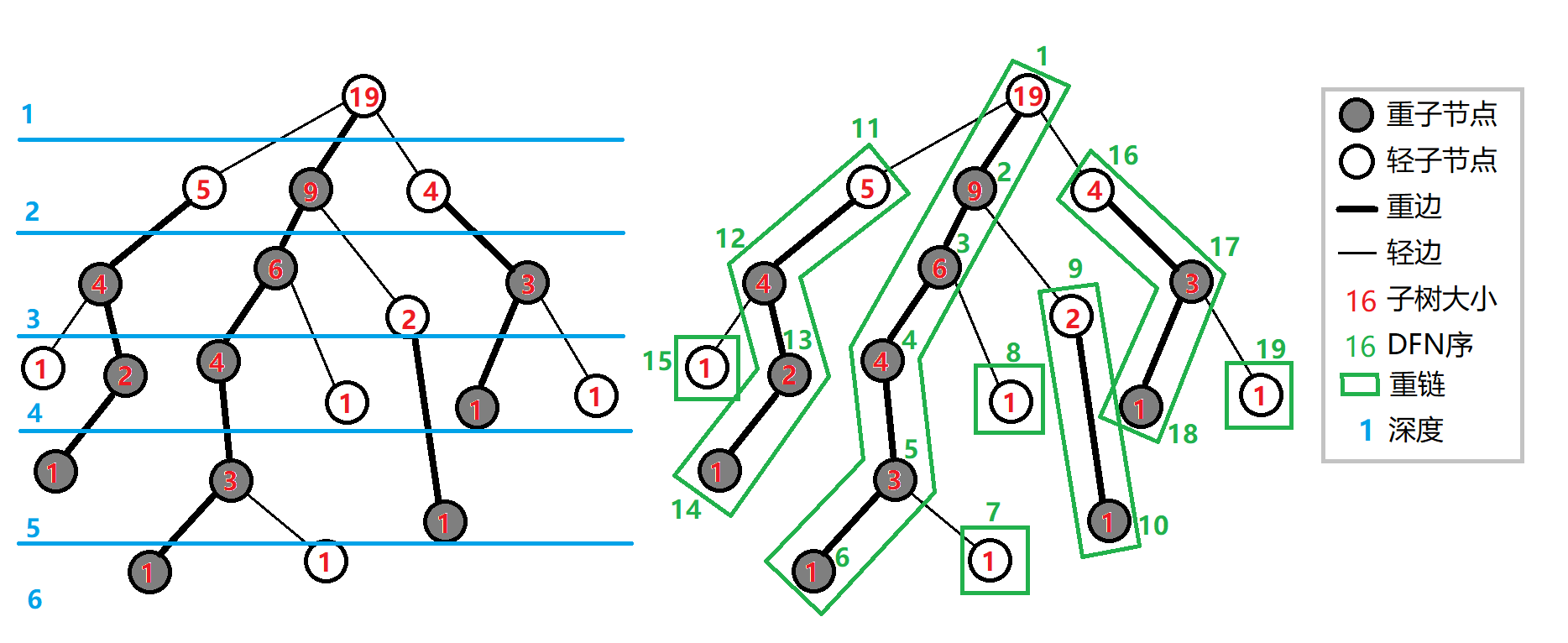
接下来我们介绍一个重要的定理： 轻重路径剖分定理 。

轻重路径剖分定理： 从树上任何一个结点出发到根结点的路径上，经过的轻边数量不会超过 O(log⁡n)O(logn) 条，经过的重链的数量也不会超过 O(log⁡n)O(logn) 条。

证明： 假设我们现在从一个叶子向根结点出发，当前走到了结点 vv ， vv 的父结点是 uu ， vv 到 uu 的路径是一条轻边。那么，我们可以推断， size[u]>2×size[v]size[u]>2×size[v] 。这是因为， vv 到 uu 是轻边，说明 uu 的重儿子不是 vv ，那么就必然存在一个其他儿子， sizesize 比 vv 的大。那么，每经过一条轻边， sizesize 就至少要翻倍，由于根结点的 size=nsize=n ，所以翻倍后不能超过 nn 。因此，只会翻 O(log⁡n)O(logn) 次，也就是最多经过 O(log⁡n)O(logn) 条轻边。

又由于任何一个结点到根结点的路径上不会出现连续的两条轻边（注意，如果有相邻的，那么两条轻边的共同端点是一条重链），所以，这条路径必然可以划分重链和轻边的交错序列，即一条重链、一条轻边、一条重链、一条轻边、......、最后一条重链。因此，经过的重链的条数也最多为 O(log⁡n)O(logn) 条。

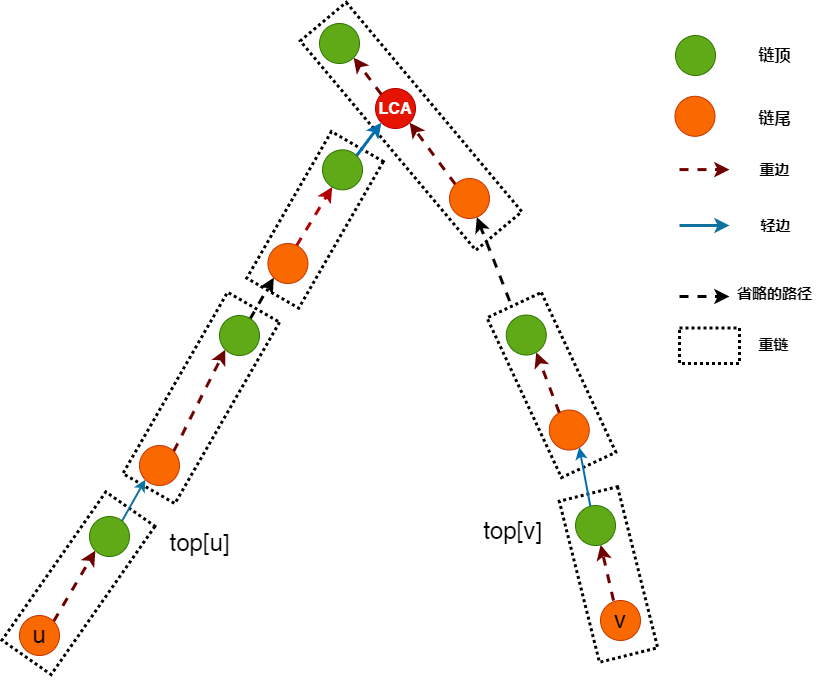
假设我们要求 LCA(u,v)LCA(u,v) ，树链剖分求 LCA 的 核心思想 是：不断地将 uu 或 vv 中链的深度较大的那个结点向上跳，每次跳跃都选择跳到当前结点所在重链的顶端的父结点。在跳跃过程中，我们会经过若干条重链（的片段）和若干条轻边。这样，当 u,vu,v 跳到同一条重链上时，LCA 就找到了。

两次 DFS：预处理 + 剖分

为了实现上面的跳跃过程，在跳之前需要准备好如下信息：

fa(x)fa(x) 表示结点 xx 在树上的父亲。
dep(x)dep(x) 表示结点 xx 在树上的深度。
siz(x)siz(x) 表示结点 xx 的子树的结点个数。
son(x)son(x) 表示结点 xx 的 重儿子 。
top(x)top(x) 表示结点 xx 所在重链的顶部结点（深度最小）。
【*】 dfn(x)dfn(x) 表示结点 xx 的 DFS 序 。
【*】 rev(i)rev(i) 表示 DFS 序中第 ii 个元素所对应的结点编号，有 rev(dfn(x))=xrev(dfn(x))=x 。

为了获取这些信息，我们可以用两次 DFS 实现。

第一次 DFS：预处理树的基本信息

计算出每个结点的父结点 fa[u]、深度 dep[u]、子树大小 siz[u]，并确定其重儿子 son[u]。

vector<int> g[N];
int n, m, root;
int dep[N], fa[N], siz[N], son[N], top[N];  // 树剖
void dfs1(int u, int f) {fa[u] = f;  dep[u] = dep[f] + 1;siz[u] = 1;for(auto v : g[u]) {if(v != f) {dfs1(v, u);siz[u] += siz[v];if(siz[son[u]] < siz[v])  // 儿子 v 更重son[u] = v;}}
}
dfs1(root, 0);

第二次 DFS：链式剖分与 DFS 序

第二次DFS是树链剖分的核心。它要确定每个结点所在重链的顶端结点 top[u]，并为每个节点分配一个新的DFS序编号 dfn[u]。这个 dfn 序非常关键，它将树上操作映射到序列上。同时，我们还需要一个映射 rev[t]，表示 dfn 序为 t 的结点是哪个原始结点。

int dfn[N], rev[N], cnt;  // DFS 序列，求解 LCA 时无需定义
void dfs2(int u, int t) {// dfn[u] = ++cnt;       // 分配 DFS 序// rev[cnt] = u;         // 记录 dfn[] 对应的原始结点top[u] = t;           // u 所在重链的顶端是 tif(!son[u]) return;   // 是叶子结点，直接返回dfs2(son[u], t);      // 优先对重儿子进行 DFS，可以保证同一条重链上的点 DFS 序连续for(auto v : g[u]) {if(v == fa[u] || v == son[u]) continue;dfs2(v, v);       // 轻儿子 v 开始一条新的重链，所以链顶是 v 自己}
}
dfs2(root, root);  // 根结点的链顶是根结点自己

注意，递归时， 优先递归重儿子 ，并且传递相同的 top 值以形成重链。 然后再遍历轻儿子 ，并且每个轻儿子是各自重链顶链顶。

求解 LCA：以链为单位向上跳

对于一个询问求解 LCA(u,v)LCA(u,v) ，考虑 u,vu,v 是否在同一条链上：

如果 top[u]=top[v]top[u]=top[v] ，即 u,vu,v 位于同一条重边组成的链上，那么说明 uu 和 vv 中深度较浅的就是 LCA， 算法结束 。
否则 top[u]≠top[v]top[u]=top[v] ，不妨假设 uu 是链顶较深的那个，即 dep[top[u]]≥dep[top[v]]dep[top[u]]≥dep[top[v]] ，如果不满足，交换 u,vu,v 即可。说明两者不位于同一条重链上，要求的 LCA 还在 u,vu,v 所在链的上方。由于 uu 所在的链更深，所以 vv 不动， uu 跳到结点 fa[top[u]]fa[top[u]] 处。
如此反复，直至 top[u]=top[v]top[u]=top[v] 即可求得 LCA。

int query(int u, int v) {while (top[u] != top[v]) {if (dep[top[u]] < dep[top[v]]) swap(u, v)u = fa[top[u]];}return dep[u] > dep[v] ? v : u;
}

graph

仍旧针对上面的模板问题，我们给出一份完整参考代码实现。

#include <bits/stdc++.h>
using namespace std;
const int N = 5e5+5;
int n, m, s, fa[N], dep[N], siz[N], son[N], top[N]; 
vector<int> g[N];
void dfs1(int u, int f) {dep[u] = dep[f] + 1;fa[u] = f;siz[u] = 1;son[u] = 0;for(int v : g[u]) {if(v != f) {dfs1(v, u);siz[u] += siz[v];if(siz[v] > siz[son[u]]) {son[u] = v;}}}
}
void dfs2(int u, int t) {top[u] = t;if(!son[u]) return;dfs2(son[u], t);for(int v : g[u]) {if(v != fa[u] && v != son[u]) {dfs2(v, v);}}
}
int query(int u, int v) {while(top[u] != top[v]) {if(dep[top[u]] < dep[top[v]]) swap(u, v);u = fa[top[u]];}return dep[u] < dep[v] ? u : v;
}
int main(){cin >> n >> m >> s;for (int i=1,u,v; i < n; i++) {cin >> u >> v;g[u].push_back(v);g[v].push_back(u);}dfs1(s, 0);dfs2(s, s);for (int i=1,u,v; i <= m; i++) {cin >> u >> v;cout << query(u, v) << '\n';}return 0;
}

One More Thing

值得一提的是，经过这两遍DFS，树就被我们“拉直”成一个序列了。如果我们在第二次 DFS 的同时记录下树的 DFS 序列 dfn[] 和结点的 DFS 序列映射 rev[]。那么，这个序列就具有两个良好的性质：

树上的任意一个子树上所有结点的 dfn 序是连续的一个区间， 对子树的操作可以转化为这个区间的操作 。
同一条重链上的结点，它们的dfn序是连续的一个区间。任意两个结点间的路径可以转化为 O(log⁡n)O(logn) 条轻边和 O(log⁡n)O(logn) 条重链。而每条重链是一个连续的区间，所以， 对树上路径的操作可以转化为 O(log⁡n)O(logn) 个区间的操作 。

基于这两个性质，我们就可以将树上的子树和路径操作转化为序列上的区间操作——这才是完整版的树链剖分思想。

【*】树链剖分在《NOI 大纲》里属于 NOI 级的知识，因此，我们（暂时）不做要求。

总结&对比

记结点数为 NN ，查询次数为 MM ，则上面各种方法的对比如下：

算法	类型	预处理时间	单次查询时间	空间复杂度	特点
暴力跳	在线	O(N)O(N)	O(N)O(N)	O(N)O(N)	简单但低效、适合对拍、允许树动态改变
倍增法	在线	O(Nlog⁡N)O(NlogN)	O(log⁡N)O(logN)	O(Nlog⁡N)O(NlogN)	常数小，适合静态树
欧拉序+RMQ	在线	O(Nlog⁡N)O(NlogN)	O(1)O(1)	O(Nlog⁡N)O(NlogN)	查询最快，常数略大
离线 TarjaN 算法	离线	O(N+M)O(N+M)	O(α(N))O(α(N)) 【均摊】	O(N+M)O(N+M)	线性时间，但只能离线处理
树链剖分	在线	O(N)O(N)	O(log⁡N)O(logN)	O(N)O(N)	空间复杂度最低

如何选择？

用来对拍算法的正确性： 适合写暴力跳，不容易写错。
查询次数不多或对查询可接受: 倍增法 是首选，代码相对好写不易错。
查询次数极大 ( M≫NM≫N )，追求 O(1)O(1) 查询: 欧拉序 + ST 表 是标准选择。
所有查询一次性给出，追求总时间最优: Tarjan 算法 效率很高，值得考虑。

掌握LCA，不仅仅是学会了一个模板、一个算法。更重要的是：

• 理解树的结构与性质: 深度、父子关系、路径唯一性。
• 掌握算法设计思想: 倍增的二进制优化、分治思想（ST表）、DFS 与数据结构（并查集）的结合、树转序列的技巧。
• 提升问题建模能力: 认识到哪些问题可以转化为LCA求解，如何将LCA作为工具解决更复杂的问题。

练习题

P4046 二叉树上的最近公共祖先 - TopsCoding —— 弱模板题
P4070 最近公共祖先（LCA） - TopsCoding —— 模板题

例题 1

Topscoding 3996 点的距离：给定一棵 nn 个点的树， QQ 个询问，每次询问点 uu 到点 vv 之间的距离。

1≤n≤1051≤n≤105 ， 1≤Q≤1061≤Q≤106

当我们会求 LCA 之后，这道题就不难了。我们处理出任意一个结点到根结点的距离 disdis ，也就是深度。易知：

disu=disfa(u)+1disu=disfa(u)+1

那么两点 x,yx,y 之间的距离就为：

disx+disy−2×dislca(x,y)disx+disy−2×dislca(x,y)

用任意一种求LCA的算法即可。

例题 2

P7241 [蓝桥杯 2022 国 B] 机房： nn 台电脑由 n−1n−1 条网线连接构成一个局域网络，任意两台电脑都可以通过网线间接相连。消息在网线中传播的时间可以忽略不计，但是消息每经过一台电脑（包括起始和目标电脑），都需要经过 dd 个单位时间的延迟才会接着传播， dd 是和这台电脑连接的电脑数量。

现在给你 mm 次询问，如果电脑 uiui 向电脑 vivi 发送信息，那么信息从 uiui 传到 vivi 的最短时间是多少?

1≤n,m≤1051≤n,m≤105

从 uiui 传到 vivi 的时间最短，必然走路径 ui→lca(ui,vi)→viui→lca(ui,vi)→vi 。

题目中的“延迟”，也就是经过一个点的所需时间，这就是点权。而我们要快速查询路径上的点权和，前缀和就是不二之选。我们从根结点开始往下遍历，设 sumisumi 表示从根结点到 ii 结点之间的延迟总和，则有：

sumu=sumfa(u)+dusumu=sumfa(u)+du

在查询的时候，路径权值和就是：

sumu+sumv−2×sumlca(u,v)+dlca(u,v)sumu+sumv−2×sumlca(u,v)+dlca(u,v)

例题 3

Topscoding4779 松鼠的新家：给定一棵 nn 个点的树，以及一个 1∼n1∼n 的排列，你需要按照排列的顺序遍历每个结点（对于排列中相邻的两个结点 pi,pi+1pi,pi+1 ，你需要从 pipi 走到 pi+1pi+1 ），排列的第一个点作为起始结点，最后一个结点作为结束结点。你想知道你重复经过了每个结点多少次。

n≤300000n≤300000

由于树上任意两个点之间的路径是唯一的，所以知道那个排列我就知道怎么走了。如果 nn 很小，那么做法也很简单，就是对于排列上相邻的两个点，求出 LCA，然后分别从两端走到 LCA，经过的结点就标记加 11 。

但是这样需要遍历。还记得我们的差分吗？当我们需要给序列中的一个区间 +1+1 的时候，我们会在 ll 处 +1+1 ，在 r+1r+1 处 −1−1 ，最后对序列求前缀和。这道题，我们是对树上的一条链 +1+1 ，想在结束的时候知道答案。

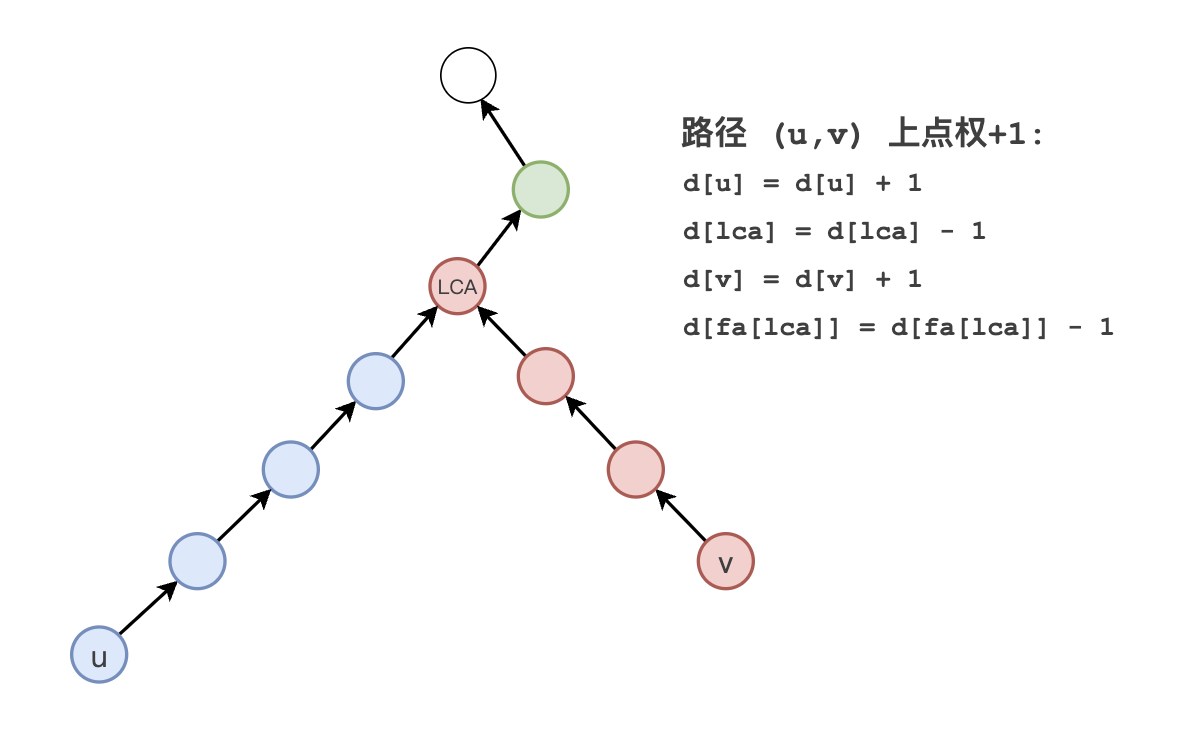
那么我们也可以做类似的操作，维护一个差分数组：对于一条从 uu 到 vv 的路径，在 uu 处 +1+1 ，在 vv 处 +1+1 ，在它们的 LCA 处 −1−1 ，在他们的 LCA 的父结点处 −1−1 。这样，在结束之后，我们从叶子往根回溯对差分数组求前缀和（DFS 的时候，先 DFS 所有的儿子，然后将儿子的差分数组的值累加起来到父亲处），就可以得到答案了。时间复杂度取决于 LCA 的求法。

这种将路径上的修改转化为路径端点以及 LCA 和 LCA 父结点处修改的方法叫做 树上差分 。（在本题中是点差分）以下图为例，可以认为图中差分公式中的前两条是对蓝色结点构成的路径进行操作，后两条是对红色结点的路径进行操作。不妨令 lcalca 左侧的蓝色节点为 leftleft 。那么有 dlca′=alca−(aleft+1)=dlca−1dlca′=alca−(aleft+1)=dlca−1 ， dfa(lca)′=afa(lca)−(alca+1)=dfa(lca)−1dfa(lca)′=afa(lca)−(alca+1)=dfa(lca)−1 。可以发现实际上点差分的操作和一维数组上的差分操作是类似的。

du←du+1dlca←dlca−1dv←dv+1dfa(lca)←dfa(lca)−1dudlcadvdfa(lca)←du+1←dlca−1←dv+1←dfa(lca)−1

例题 4

Topscoding 7510 道路修复：给定 nn 个结点的一棵树，给定 mm 条路线，第 ii 条路线从结点 xixi 到结点 yiyi 。统计树上有多少条边被路线经过至少 kk 次。

1≤n,m≤5×1061≤n,m≤5×106 ， 1≤k≤m1≤k≤m

和上一题做一下对比，上一题，我们需要统计每个结点被经过几次。在这一题中，我们需要统计每条边被经过几次。

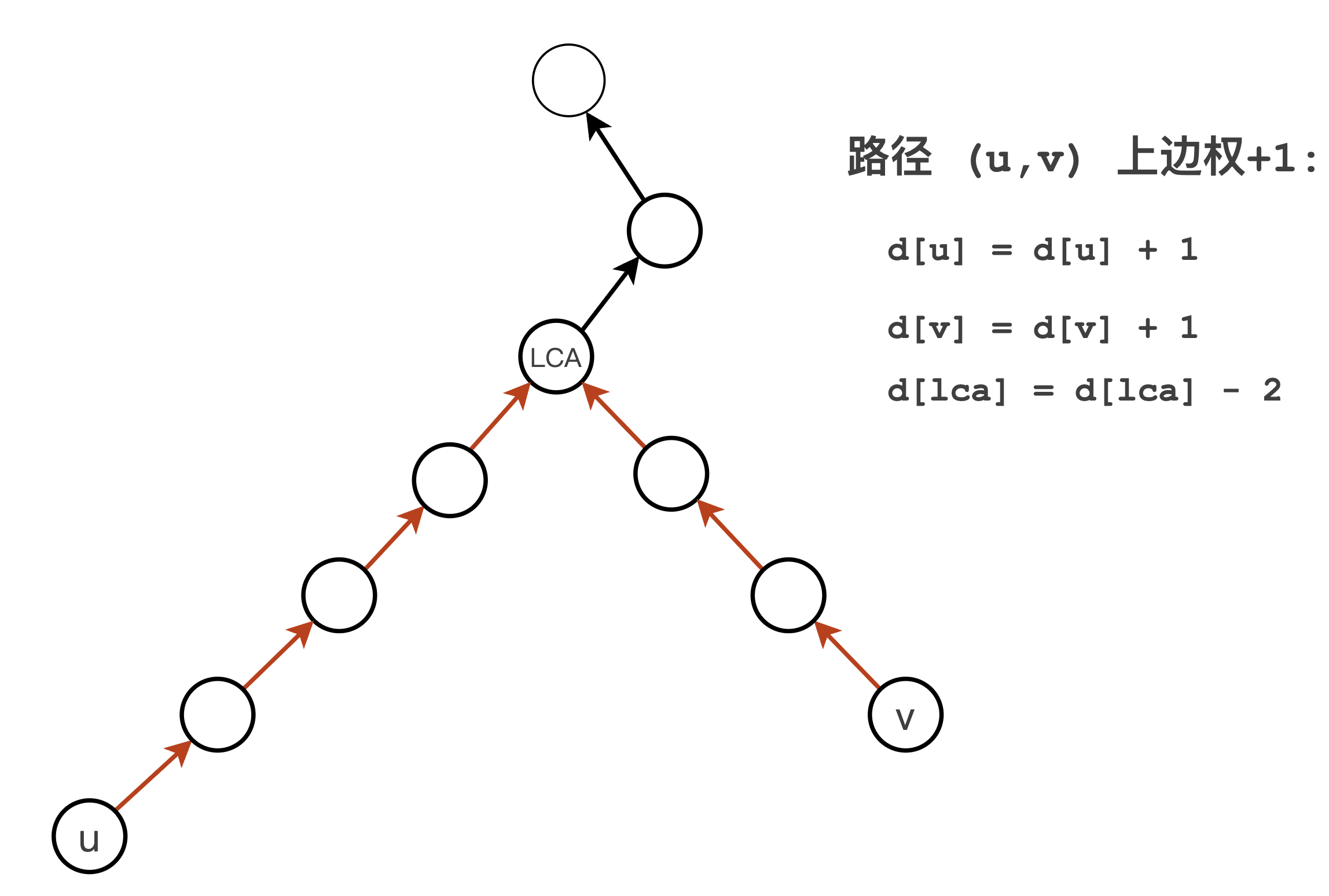
类似上一题的点差分，这里我们做 边差分 。由于 在边上直接进行差分比较困难 ，可以将本来应当累加到红色边上的值向下移动到子结点里，那么操作起来也就方便了。差分修改公式如下，和点差分的原理类似，同样是对两段区间进行差分。

du←du+1dv←dv+1dlca←dlca−2dudvdlca←du+1←dv+1←dlca−2

明白了树上边差分怎么做，这题就很好处理了。除了差分的更新公式不同，边差分和点差分没有什么区别。

例题 5

Topscoding 3997 暗的连锁：有一个 nn 个结点的图，有 n−1n−1 条主要边，和 mm 条次要边，保证主要边形成一棵树。现在你需要在主要边和次要边中各选一条删除，使得这个图不连通。问有多少种方案。

n≤105,m≤2×105n≤105,m≤2×105

我们可以先枚举主要边，然后对次要的边进行计数。切掉一条主要边，相当于树被切成了两个部分，我们关心这两个部分之间有多少条次要边连着。我们会发现，如果树的这两个部分：

有 22 条及以上的次要边连着，那么我们无法使得这个图不连通。
如果只有一条次要边连着，我们只有一种切法，即选择该次要边并切断。
如果没有次要边连着，我们有 mm 种不同的次要边选法。

那么，问题就转化为：对每条主要边，求切掉它以后有几条次要边连着树的两个部分。

我们考虑一条次要边 (u,v)(u,v) ，当我们切掉 uu 到 vv 在主要边构成的树上的唯一路径上的边时，这条次要边才会起到连接两个断开的部分的功能，否则不提供该功能。因此，每条次要边 (u,v)(u,v) 只对主要边构成的树上 uu 和 vv 之间的唯一路径上的主要边的计数产生 +1+1 的贡献。

所以我们可以枚举每条次要边 (u,v)(u,v) ，给 u,vu,v 由主要边构成的唯一路径上的所有边的计数 +1+1 。这种路径 +1+1 就是上面一题提到的树上的边差分来实现的。

最后，枚举每条主要边，然后分为上面三类讨论统计即可。

例题 6

Topscoding 1183 [NOIP 2013 提高组] 货车运输：A 国有 nn 座城市，编号从 1 到 nn ，城市之间有 mm 条双向道路。每一条道路对车辆都有重量限制，简称限重。现在有 qq 辆货车在运输货物，第 ii 辆货车从城市 uiui 向 vivi 运输。司机们想知道每辆车在不超过车辆限重的情况下，最多能运多重的货物。

0<n<100000<n<10000 ， 0<m<500000<m<50000 ， 0<q<300000<q<30000

货物要尽可能重意味着路径上的最小边权尽可能大，如果我们想要两个结点之间经过的最小边权最大，那么我们就沿着最大生成树的边行走即可。

所以这道题的第一步就是，求出最大生成树。在这之后，任意两个点之间的路径就变得唯一了。

现在问题就变成了：给出 qq 次询问，每次询问给出两个结点，询问它们在树上的唯一路径的最小边权。

对于这条唯一路径，根据我们之前说过的，可以拆成 uu 到 LCA 的路径，以及 LCA 到 vv 的路径。我们可以利用树上倍增的方法，用 f[i][k]f[i][k] 表示从 ii 点出发，到其第 2k2k 级祖先， dp[i][k]dp[i][k] 表示从 ii 点出发，到其第 2k2k 级祖先所经过的边的最小边权。预处理时，有

f[i][k]=f[f[i][k−1][k−1]dp[i][k]=min(dp[i][k−1],dp[f[i][k−1]][k−1])f[i][k]dp[i][k]=f[f[i][k−1][k−1]=min(dp[i][k−1],dp[f[i][k−1]][k−1])

预处理完以后，我们可以将 uu 到 LCALCA 的路径拆成 log⁡nlogn 段这样的路径，将这些路径拼在一起取 min⁡min 即可。求最小边权的过程和倍增求 LCA 可以同步进行。

用倍增法求 LCA 的单次询问的时间为 O(log⁡n)O(logn) 。