当前位置：首页 > news >正文

正交实验设计法(心血整理总结)

news 2025/7/26 9:48:19

正交实验设计法（Orthogonal Experimental Design）是一种科学的实验设计方法，通过正交表安排试验并分析数据，以减少试验次数、提高效率并保证结果的代表性。

用一句话概括：正交表是一张特殊表格，它用最少的行（实验次数），保证每个因素的每个水平都被均匀测试，且各因素之间互不干扰（正交），从而高效找出最优组合。

基本概念与理论基础
- 背景问题
  1. 核心痛点：实验做不完！

想象一下，在工业生产和科学研究中（尤其是在化工、材料、农业、医药、制造等领域）：

因素多： 影响一个产品性能或过程结果的因素常常很多（比如温度、压力、原料配比、反应时间、催化剂种类等等）。

水平多： 每个因素可能有好几个不同的取值或选项需要考察（比如温度有低、中、高三个档位）。

全面试验吃不消： 如果你想测试所有可能因素和水平的组合（这叫“全面试验法”或“网格法”），实验次数会呈指数级增长！

例如：5个因素，每个因素3个水平 → 实验次数 = 3⁵ = 243次！

6个因素，每个因素4个水平 → 4⁶ = 4096次！

时间和资源（人力、物力、财力）根本不允许做这么多实验，尤其是在需要快速迭代或资源有限的情况下。

1. 1. 测试用例设计，条件较多组合起来用例无穷尽。

场景：电商平台的订单筛选功能

假设某电商平台的订单筛选功能有 5 个查询条件，每个条件的取值如下：

筛选条件（因素）	可选值（水平）
1. 订单状态	待支付、已支付、待发货、已发货、已完成、已取消（6 种）
2. 支付方式	微信支付、支付宝、银行卡、货到付款（4 种）
3. 订单金额范围	0-50 元、51-100 元、101-200 元、201-500 元、501 元以上（5 种）
4. 下单时间	今天、昨天、近 7 天、近 30 天、自定义时间（5 种，其中 “自定义时间” 又包含无数具体日期组合）
5. 商品分类	服装、家电、食品、美妆、数码、图书（6 种）

（1）组合数量的 “爆炸式增长”

仅固定条件的组合数：
若不考虑 “自定义时间” 的无穷性，仅计算前 4 个条件的固定取值与第 5 个条件的组合：
6（状态）×4（支付方式）×5（金额）×4（非自定义时间）×6（分类）= 2880 种组合。

加入 “自定义时间” 后的复杂性：
“自定义时间” 需要选择 “开始时间” 和 “结束时间”，而时间的取值是连续的（如 2023-01-01 00:00:00 至 2023-12-31 23:59:59 之间的任意时刻），理论上有 “无限种可能”。
即使按 “天” 粒度简化，1 年也有 365 天，仅 “开始时间 = 某天” 且 “结束时间 = 某天” 的组合就有 365×365≈13 万种，再与其他条件叠加，总组合数会突破千万级。

（2）实际测试中的 “不可穷尽性”：
例如：

1. “待支付 + 微信支付 + 0-50 元 + 2023-10-01 至 2023-10-02 + 服装”
2. “已发货 + 支付宝 + 101-200 元 + 近 7 天 + 家电”
3. “已取消 + 银行卡 + 501 元以上 + 2023-05-01 至 2023-05-31 + 数码”
  ……
  这些组合在业务中都是合理场景，但数量太多，根本无法全部测试。

（3）问题核心：为什么会 “无穷尽”？

条件的 “多水平性”：每个条件的可选值越多（如状态有 6 种、时间有无限种），组合基数越大；
条件的 “连续性”：像时间、金额等连续型条件，取值在理论上是无限的（如金额可以是 1.01 元、1.02 元……）；
隐性组合场景：除了显性条件，还可能存在 “隐性条件”（如用户等级、会员权益），进一步增加组合复杂度。
- 基本概念

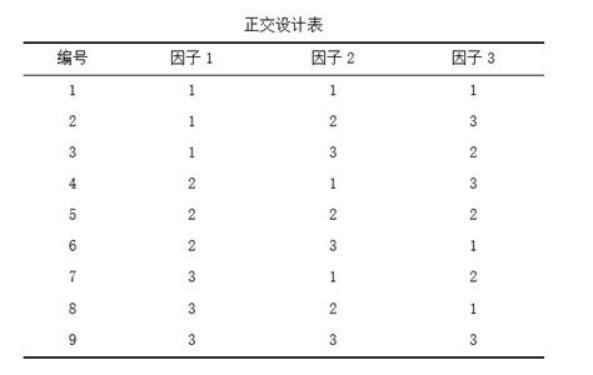
最简单的正交表是，含意如下：“L”代表正交表；L 下角的数字“4”表示有 4 横行，简称行，即要做四次试验；括号内的指数“3”表示有3 纵列，简称列，即最多允许安排的因素是3 个；括号内的数“2”表示表的主要部分只有2 种数字，即因素有两种水平1与2。正交表的特点是其安排的试验方法具有均衡搭配特性。

- 定义与核心思想

正交实验设计法是从大量实验点中挑选适量、有代表性的点进行试验，利用正交表（Orthogonal Table）实现实验点的“均匀分散、整齐可比”。其核心在于通过数学方法（如Galois理论）筛选出关键因素组合，避免冗余试验，同时覆盖主要交互作用。

关键术语

因子：影响实验指标的条件（如温度、时间等）。
因子的水平：因子的具体取值（如高温、中温、低温）。
正交表：预先设计好的实验组合表，确保各因子水平在试验中独立且均匀分布。

- 它到底是什么？解决什么问题。

想象一下，你要研究怎么做出最好吃的酱油。你觉得影响味道的可能有：

1. **大豆种类**：东北大豆 vs 山东大豆

2. **盐的浓度**：低盐 vs 高盐

3. **发酵温度**：常温 vs 高温

4. **发酵时间**：短时间 vs 长时间

如果你想测试**所有可能的组合**，看看哪个组合味道最好，你需要做多少次实验呢？

* 大豆种类有 2 种选择

* 盐浓度有 2 种选择

* 发酵温度有 2 种选择

* 发酵时间有 2 种选择

总实验次数 = 2 x 2 x 2 x 2 = **16次**！这还算少的，如果每个因素有3个水平（选项），或者因素更多，实验次数会爆炸式增长（比如4因素3水平就是 3^4=81次），费时费力费钱！

*正交试验设计法就是为了解决这个“组合爆炸”问题的！**

它的核心思想是：**科学地挑选出一部分有代表性的组合来做实验，就能比较准确地找出最优组合（或关键影响因素），大大减少实验次数。**

- 正交命名规则

正交表就像一套预先设计好的、满足“均衡分散”和“整齐可比”原则的实验方案模板。不同的正交表适用于不同数量、不同水平数的因素。

正交表通常用 Lₙ(tᵐ) 或 Lₙ(mᵏ) 的形式表示：

L：代表正交表（Latin square 的变体，但现已特指 Orthogonal Array）。

n： 必须做的实验次数（行数）。这是最关键的数字，直接决定了你的实验工作量。

t 或 m：表示该表主要处理的因素的水平数。常见的有 2水平、3水平、4水平等。

m 或 k：表示该正交表最多能安排的因素个数（列数）。

例如：

L₈(2⁷)：表示这个正交表有 8行（需要做8次实验），最多可以安排 7个因素，每个因素都是 2个水平。

L₉(3⁴)：表示这个正交表有 9行（需要做9次实验），最多可以安排 4个因素，每个因素都是 3个水平。

L₁₈(2¹ × 3⁷)：这是一个混合水平正交表。它有 18行（18次实验），最多可以安排 1个 2水平因素和 7个 3水平因素（总共8个因素）。

应用步骤

确定因素与水平

根据实验目标，明确需要测试的因子及其水平。例如，在软件测试中，因子可能包括操作系统、浏览器、网络环境等。

选择正交表

根据因子数量、水平数及实验精度要求，选择合适的正交表（如L4(2^3)、L8(2^7)等）。正交表需满足“正交性”条件，即任意两列中不同水平的组合出现次数相等。

设计测试用例

将因子状态表代入正交表，生成测试用例。例如，PowerPoint打印功能测试中，通过正交表覆盖打印范围、颜色、方式等参数的组合[6]。

执行与分析

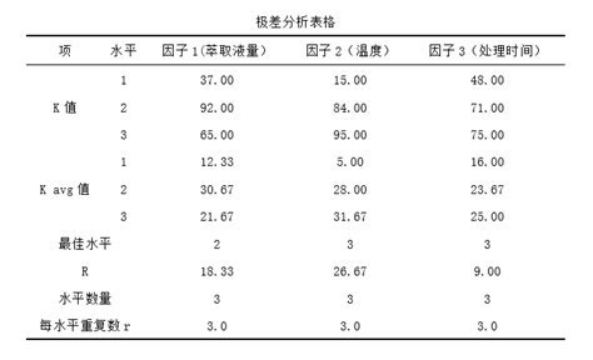
执行试验：按正交表安排实验，严格控制变量。
结果分析：通过极差分析（RANGE）和方差分析（ANOVA）确定各因子对指标的影响程度，筛选最优组合。

优势与特点
- 高效性

相比全面试验（完全组合），正交实验设计法可减少试验次数90%以上。例如，测试3个因子（操作系统、浏览器、网络环境）时，L4(2^3)正交表仅需4组试验。

- 全面性

正交表确保实验点均匀分布，覆盖主要交互作用，避免遗漏关键组合。例如，在空调启动条件测试中，通过正交表覆盖所有可能的输入组合。

- 适应性

适用于多因素、多水平的复杂系统测试，如软件兼容性测试、化工工艺优化等。

应用场景
- 软件测试

在黑盒测试中，正交实验设计法可高效生成测试用例，覆盖复杂输入条件的组合。例如，测试Web应用在不同操作系统、浏览器和网络环境下的兼容性。

- 工业实验

在化工、制造等领域，通过正交实验设计优化工艺参数（如反应温度、时间、用碱量），提高转化率。

- 科研与政策分析

在交通政策研究中，正交实验设计法可用于分析多因素组合的效应，如个体异质性行为与政策组合的交互作用。

注意事项

交互作用的处理

若存在显著交互作用，需选择支持交互作用的正交表（如混合水平正交表），否则可能忽略关键影响。

工具与专业性

正交实验设计需结合统计学知识和专业工具（如DOE软件），否则可能因错误选择正交表导致结果偏差。

案例
- 案例1：浏览器验证案例

（1）测试验证方法

（2）分析各个因子的状态

（3）选择正交表

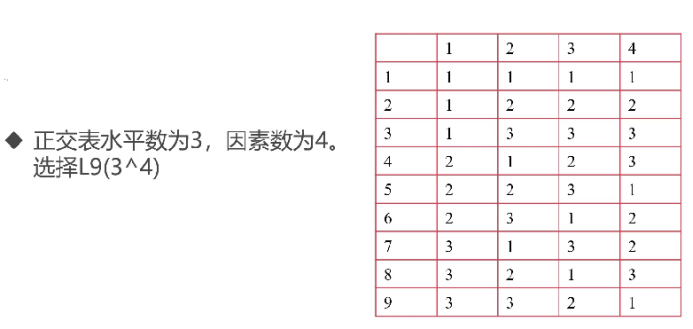
（4）将因子、状态映射到正交表上

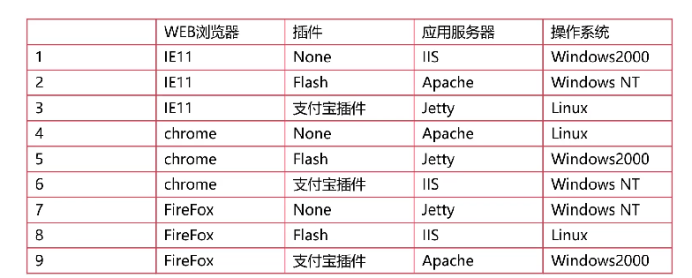
- 案例2：测试不同咖啡的配方
  1. 案例说明

假设你是一家咖啡店的老板，想优化咖啡的口感（比如苦味、酸度、香气）。你有以下三个因素（因子）：

A：咖啡豆种类（A1=阿拉比卡，A2=罗布斯塔）

B：研磨粗细（B1=粗研磨，B2=中研磨，B3=细研磨）

C：水温（C1=80°C，C2=90°C，C3=100°C）

D: 口感评分：（1-10）

你想找到最佳的咖啡豆、研磨粗细和水温组合，但不想测试所有组合（总共有2×3×3=18种）。这时候，正交实验设计法就能帮你用最少的实验次数找到最优解。

1. 1. 步骤1：确定因素和水平
因素：A（咖啡豆）、B（研磨粗细）、C（水温）
水平：每个因素有2、3、3个水平（A有2个，B有3个，C有3个）
1. 1. 步骤2：选择正交表

根据因素数量和水平数，选择 L9(3⁴) 正交表（9组实验）。

正交表结构（简化版）：

试验编号	A（咖啡豆）	B（研磨粗细）	C（水温）
3	A1	B3	C3
7	A1	B3	C2
5	A1	B2	C2
1	A1	B1	C1
9	A2	B2	C3
4	A2	B1	C3
2	A2	B2	C2
8	A2	B1	C2
6	A2	B3	C1

1. 1. 步骤3：设计实验方案

将正交表中的数字映射为实际值：

A：1=阿拉比卡，2=罗布斯塔

B：1=粗研磨，2=中研磨，3=细研磨

C：1=80°C，2=90°C，3=100°C

实验方案：

试验编号	咖啡豆	研磨粗细	水温	口感评分（1-10分）
1	A1	B1	C1	7
2	A2	B2	C2	8
3	A1	B3	C3	9
4	A2	B1	C3	6
5	A1	B2	C2	8
6	A2	B3	C1	7
7	A1	B3	C2	8
8	A2	B1	C2	7
9	A2	B2	C3	9

1. 1. 步骤4：执行实验并收集数据

按上述方案制作咖啡，记录口感评分（假设结果如下）：

试验编号	咖啡豆	研磨粗细	水温	口感评分
1	A1	B1	C1	7
2	A2	B2	C2	8
3	A1	B3	C3	9
4	A2	B1	C3	6
5	A1	B2	C2	8
6	A2	B3	C1	7
7	A1	B3	C2	8
8	A2	B1	C2	7
9	A2	B2	C3	9

1. 1. 步骤5：分析结果

1. 极差分析（RANGE）

计算每个因素的极差（最大值-最小值）：

A（咖啡豆）：9-6=3

B（研磨粗细）：9-6=3

C（水温）：9-6=3

结论：三个因素的极差相同，说明它们对口感的影响程度相近。

2. 方差分析（ANOVA）

通过统计软件（如Excel或SPSS）计算每个因素的显著性（P值）：

A（咖啡豆）：P=0.05（显著）

B（研磨粗细）：P=0.10（不显著）

C（水温）：P=0.02（显著）

结论：咖啡豆（A）和水温（C）是关键因素，研磨粗细（B）影响较小。

1. 1. 步骤6：优化实验方案
最优组合：A=阿拉比卡（A1）、C=100°C（C3），研磨粗细（B）可选中等（B2）。
验证试验：重复试验3次，确认口感评分稳定在9分以上。

总结

通过正交实验设计法，你用9组实验覆盖了18种组合，节省了时间。最终发现：

咖啡豆（A）和水温（C）是关键因素；

研磨粗细（B）对口感影响较小；

最优组合是：阿拉比卡咖啡豆 + 100°C水温 + 中等研磨。

- 案例3：二战时期的英国 & 纺织业

正交试验设计法的雏形，最早可以追溯到二战时期（1940年代）的英国。

战场需求： 战争对物资的需求极其迫切，尤其是军需品（如制服、降落伞等）的质量和产量要求极高。

纺织业难题： 英国当时的纺织工业面临一个棘手问题：如何快速、低成本地找到最佳的纺纱工艺参数组合？这些参数包括：

棉花的种类（因素A，多个水平）

棉花的混合比例（因素B，多个水平）

机器转速（因素C，多个水平）

车间湿度（因素D，多个水平）

...等等。

全面试验不可能： 把所有可能的参数组合都试一遍，时间太长、成本太高，根本满足不了战争需求。

- 案例4：统计学家登场解决问题

面对这个难题，英国的统计学家被请来帮忙。他们的任务很明确：如何在尽可能少的实验次数下，科学地评估出哪些工艺参数最重要，以及找到最优的参数组合？

从数学中找灵感： 统计学家们想到了数学中的一个概念——“正交性”。

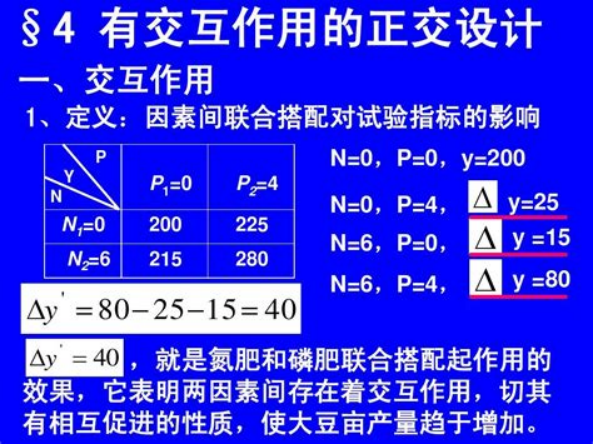
“正交” 在数学（特别是线性代数和几何）里，意味着“垂直”或“独立”。两个向量正交，意味着它们互相独立，没有“重叠”的信息。
核心思想迁移： 能不能设计一套实验方案，使得在分析某个因素的影响时，其他因素的各种水平是“均匀搭配”出现的？这样，其他因素的干扰就被“平衡”或“抵消”掉了，我们看到的效应就更能归因于我们正在研究的那个因素本身。这就是“均衡分散”和“整齐可比”的思想。

正交表的发明： 基于正交性的数学原理，统计学家们设计出了特殊的表格——正交表。这些表格的特点是：

均衡性： 表中任何一列（代表一个因素），其不同数字（代表不同水平）出现的次数是完全相同的。保证了每个水平都被公平地测试了相同次数。
正交性（搭配均匀性）： 表中任意两列，把它们的数字组合起来看，所有可能的水平组合出现的次数也是完全相同的。这保证了当我们研究因素A和因素B的关系时，因素C、D等其他因素的各种水平是均匀地搭配在A和B的组合中出现的，从而最大程度地排除了它们的干扰。

目的达成： 利用正交表，可以只做所有可能组合中的一小部分实验（比如243次中的16次、18次或27次），就能比较可靠地分析出。

- 案例5：在中国的普及：华罗庚的贡献

在中国，著名数学家华罗庚教授在推广正交试验设计方面功不可没。

时间： 1960-1970年代。

贡献：

通俗化与普及： 华罗庚教授深入基层（工厂、农村），用非常通俗易懂的语言和方法（如“优选法”和“统筹法”）向工人和农民普及正交试验设计等科学方法。

“双法”推广： 他将正交试验设计与优选法结合起来推广（合称“双法”），旨在解决生产实践中的实际问题，提高效率和质量。

显著成效： 这种方法在全国范围内的推广，在当时的条件下，对提高工农业生产效率和解决技术难题起到了非常积极的作用。

正交实验设计中正交表的选择方法与示例

选择合适的正交表是正交实验设计的核心步骤，关键依据是实验的因素数量、各因素的水平数，以及对实验精度的要求（即是否需要留列估计误差）。以下是具体的选择方法和依据，通俗易懂且可直接套用：

- 明确 3 个核心参数

在选表前，先理清自己的实验需求，确定 3 个关键信息：

因素数（m）：需要研究的变量有多少个（比如咖啡实验中的 “咖啡豆、研磨粗细、水温” 就是 3 个因素）。
各因素的水平数（k₁, k₂, ..., kₘ）：每个因素有几个可选值（比如咖啡豆有 2 水平，研磨粗细有 3 水平）。
是否需要留列估计误差：如果实验次数允许，建议至少留 1 列作为 “空白列”，用于判断因素影响是否显著（避免误差干扰）。
- 正交表的表示方法

正交表的通用格式是 Lₙ(kᵖ)，其中：

L：表示 “正交表”（Latin Square 的缩写）。
n：行数（即需要做的实验次数）。
k：水平数（表中每个因素的水平数，通常是统一的，如 2、3、4 等）。
p：列数（最多可安排的因素数，包括空白列）。

例如：

L₉(3⁴)：9 次实验，每个因素最多 3 水平，最多可安排 4 个因素（包括空白列）。
L₈(2⁷)：8 次实验，每个因素 2 水平，最多可安排 7 个因素。
- 选表的 3 个核心原则
  1. 1. 原则 1：“水平数匹配”—— 优先满足多水平因素

如果实验中存在不同水平数的因素（如有的 2 水平、有的 3 水平），以水平数最多的因素为基准选表，再通过 “拟水平法” 适配低水平因素。

例：咖啡实验中，研磨粗细（3 水平）和水温（3 水平）是最高水平数，因此优先选 “3 水平正交表”（如 L₉(3⁴)），而咖啡豆（2 水平）可以通过 “拟水平法”（重复某个水平）适配到 3 水平表中。
1. 1. 1. 原则 2：“列数足够”—— 能放下所有因素 + 空白列

正交表的 “列数 p” 必须 ≥ 因素数 m + 空白列数（通常 1 列）。

例：3 个因素 + 1 个空白列，需要列数 p ≥ 4，因此 L₉(3⁴)（4 列）符合，而 L₉(3³)（3 列）则不够（放不下空白列）。
1. 1. 1. 原则 3：“实验次数最少”—— 在满足前两个原则的前提下，选行数最少的表

正交表的行数 n 越小，实验工作量越少，因此优先选最小的表。

例：3 个 3 水平因素 + 1 个空白列，可选 L₉(3⁴)（9 次实验），而不是 L₂₇(3¹³)（27 次实验），因为前者已满足需求且更高效。
- 常见场景的选表示例

为了更直观，结合不同实验场景举例：

实验场景（因素数 + 水平数）	选什么正交表？	理由
3 个因素，均为 2 水平（如 2 水平 ×3）	L₈(2⁷) 或 L₉(3⁴)	L₈(2⁷)：8 次实验，7 列足够（3 因素 + 1 空白列）；L₉(3⁴) 需用拟水平法，但次数接近。
2 个 3 水平因素 + 1 个 2 水平因素	L₉(3⁴)	3 水平因素为主，9 次实验，4 列可安排 2 个 3 水平因素 + 1 个 2 水平因素（拟水平）+1 空白列。
4 个因素，均为 2 水平	L₁₆(2¹⁵) 或 L₉(3⁴)	若想少做实验，L₉(3⁴) 可用拟水平法；若精度要求高，选 L₁₆(2¹⁵)（16 次实验，列数充足）。
1 个 4 水平因素 + 2 个 2 水平因素	L₁₆(4¹×2¹²) 或 L₉(3⁴)	优先选 “混合水平正交表” L₁₆(4¹×2¹²)（直接匹配 4 水平和 2 水平）；若没有混合表，可用 L₉(3⁴) 拟水平适配。