leetcode110：判断平衡二叉树（两种思路对比）

题目链接： LeetCode 110：判断一棵二叉树是否是“平衡二叉树”，【难度：简单；通过率：59.5%】

这道题不仅考察对二叉树性质的理解，更是展示如何将一个朴素的递归解法优化为高效解法的绝佳案例

一、 题目描述

给定一个二叉树，判断它是否是高度平衡的二叉树

在本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1

示例:

示例 1:

给定二叉树 [3,9,20,null,null,15,7]3/ \9  20/  \15   7
返回 true

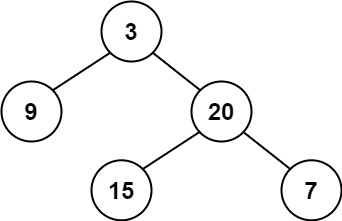
示例 2:

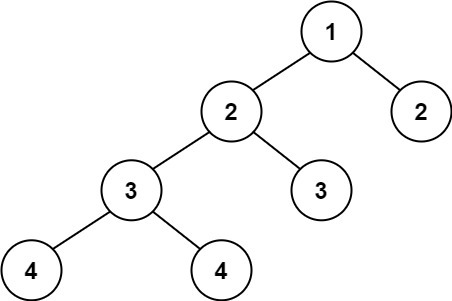
给定二叉树 [1,2,2,3,3,null,null,4,4]1/ \2   2/ \3   3/ \4   4
返回 false

---

二、 核心思路分析

题目的关键在于“每个节点”。这意味着我们不能只判断根节点的左右子树高度差，而是要确保树中的所有节点都满足这个条件。这天然地引出了递归的思想

1. 方法一：自顶向下的简单递归

最直观的想法是：

1. 对于当前节点 root，我们先判断它自身是否平衡。这需要我们分别计算其左子树的高度和右子树的高度，然后看它们的差值是否小于等于 1
2. 如果当前节点满足条件，我们不能就此罢休，还必须递归地去判断它的左子树和右子树是否也是平衡的
3. 只有当当前节点、左子树、右子树都平衡时，整棵树才算平衡

这是一种“自顶向下”的思路，先判断顶层，再深入子层

1.1 代码实现 (方法一，非最优解)

【一种参考代码】：

class Solution {// 主函数：判断树是否平衡public boolean isBalanced(TreeNode root) {// 空树是平衡的if (root == null) {return true;}// 1. 判断当前节点是否平衡if (Math.abs(getDepth(root.left) - getDepth(root.right)) > 1) {return false;}// 2. 递归地判断左右子树是否平衡// 只有当左右子树都平衡时，整棵树才平衡return isBalanced(root.left) && isBalanced(root.right);}// 辅助函数：获取以 root 为根的子树的最大高度public int getDepth(TreeNode root) {if (root == null) {return 0;}return Math.max(getDepth(root.left), getDepth(root.right)) + 1;}
}

1.2 效率分析

但是，这个方法存在严重的重复计算问题：

当我们调用 isBalanced(root) 时，getDepth 会遍历整个左子树和右子树。然后，当我们递归调用 isBalanced(root.left) 时，getDepth 又会再次遍历 root.left 的所有子节点。节点被反复遍历，导致时间效率低下

• 时间复杂度：对于平衡树是 O(N log N)，对于退化成链表的树是 O(N²)
• 空间复杂度：O(H)，递归栈的深度，最坏为 O(N)

下面讲解更好的递归解法

2. 方法二：自底向上的高效递归 (后序遍历)

为了避免重复计算，我们可以换一种思路。能不能在一次递归中，既能获取子树的高度，又能知道它是否平衡呢？

答案是可以的！我们可以采用“自底向上”的思路，这与后序遍历（左-右-根）的顺序不谋而合

1. 我们先递归到最深的叶子节点
2. 在回溯（返回）的过程中，我们既计算当前节点的高度，也顺便判断它是否平衡
3. 我们约定一个特殊的返回值，比如 -1，来表示“这棵子树已经不平衡了”
4. 如果一个子树的递归调用返回了 -1，我们就知道没必要再继续计算了，直接将 -1 继续向上传递，实现**“剪枝”**

2.1 代码实现 (方法二)

【一种参考代码】：

class Solution {// 主函数：通过调用辅助函数并检查其返回值来判断public boolean isBalanced(TreeNode root) {// 如果 getHeight 返回 -1，说明树不平衡；否则平衡return getHeight(root) != -1;}/*** 辅助函数：在计算高度的同时判断是否平衡* @return 如果以 root 为根的子树是平衡的，则返回其高度；否则返回 -1*/public int getHeight(TreeNode root) {// 基准情况：空节点高度为 0，是平衡的if (root == null) {return 0;}// 1. 递归获取左子树的高度（后序遍历的“左”）int leftHeight = getHeight(root.left);// 如果左子树已经不平衡，立即剪枝，返回 -1if (leftHeight == -1) {return -1;}// 2. 递归获取右子树的高度（后序遍历的“右”）int rightHeight = getHeight(root.right);// 如果右子树已经不平衡，立即剪枝，返回 -1if (rightHeight == -1) {return -1;}// 3. 处理当前节点（后序遍历的“根”）// 判断当前节点是否平衡if (Math.abs(leftHeight - rightHeight) > 1) {// 如果不平衡，返回 -1return -1;} else {// 如果平衡，返回当前子树的真实高度return Math.max(leftHeight, rightHeight) + 1;}}
}

2.2 效率分析

通过这种自底向上的后序遍历方式，每个节点只被访问一次。我们在计算高度的同时完成了平衡性的判断

• 时间复杂度：O(N)，因为每个节点只访问一次
• 空间复杂度：O(H)，递归栈的深度，最坏为 O(N)

---

三、 总结与对比

特性	方法一 (自顶向下)	方法二 (自底向上 / 后序遍历)
思路	先判断当前节点，再递归判断子节点	先递归处理子节点，再根据子节点信息判断当前节点
遍历顺序	类似前序遍历	后序遍历
效率	低，存在大量重复计算	高，每个节点只访问一次
时间复杂度	O(N log N) ~ O(N²)	O(N)
关键点	分别用 isBalanced 和 getDepth 两个递归函数	用一个递归函数 getHeight 和特殊返回值 -1 完成所有工作

当发现一个“自顶向下”的解法存在重复计算时，不妨尝试一下“自底向上”的思路，看看能否在**回溯时“顺便”**解决问题