图像梯度处理与边缘检测
在图像处理的世界里,我们常常需要从复杂的像素矩阵中提取有意义的信息 —— 比如一张照片中物体的轮廓、医学影像中病灶的边界、自动驾驶视野里的道路边缘。这些 “边界” 或 “轮廓” 在专业术语中被称为 “边缘”,而捕捉边缘的核心技术,离不开对 “图像梯度” 的理解与处理。
目录
一、图像梯度
1. 梯度的数学基础:从偏导数到梯度向量
2. 梯度处理:用算子捕捉变化
Sobel算子
Laplacian算子
二、边缘检测:从梯度到清晰边界
1. 边缘检测的前提:降噪处理
2. 计算图像的梯度与方向
3.非极大值抑制
4.双阈值筛选
5.API的使用
三、理论到实践:梯度与边缘检测的应用
总结
一、图像梯度
想要理解边缘检测,首先要抓住 “梯度” 这个核心概念。在数学中,梯度是描述函数变化率的向量,它既包含变化的 “大小”(强度),也包含变化的 “方向”。而在图像中,每个像素的灰度值(或 RGB 值)可以看作是一个二维函数,图像梯度就是这个函数在像素层面的变化率。
1. 梯度的数学基础:从偏导数到梯度向量
图像是由离散的像素组成的二维网格,假设我们用f(x,y)表示坐标f(x,y)处的灰度值(0-255,黑色到白色)。那么:
- 横向梯度(x 方向):用偏导数
表示,描述像素在水平方向的灰度变化率(比如从左到右变亮或变暗);
- 纵向梯度(y 方向):用偏导数
表示,描述像素在垂直方向的灰度变化率(比如从上到下的灰度突变)。
梯度向量则是由这两个偏导数组成的向量,它的大小(模长)表示灰度变化的 “剧烈程度”,方向则指向灰度增长最快的方向 —— 这正是边缘的核心特征:边缘处的灰度变化往往最剧烈,梯度大小也最大。
2. 梯度处理:用算子捕捉变化
在实际计算中,图像是离散的,无法直接求偏导数,因此需要用 “算子”(即小矩阵)通过卷积运算近似计算梯度。常用的梯度算子有以下几种:
Sobel算子
sobel算子常被用在图像的垂直方向边缘提取或水平方向边缘提取,如果你还记得高数中用一阶导数来求极值的话,就很容易理解了:把图片想象成连续函数,因为边缘部分的像素值是与旁边像素明显有区别的,所以对图片局部求极值,就可以得到整幅图片的边缘信息了。不过图片是二维的离散函数,导数就变成了差分,这个差分就称为图像的梯度。sobel算子本质就是一阶导数求极值。所以只适用于二维的边缘,对垂直和平行一起提取,效果不好。
比较常用的sobel垂直边缘提取:,水平:
但sobel算子的卷积核中的值没有明确规定你可以用你自己的。比如,最初只利用邻域间的原始差值来检测边缘的Prewitt算子:
还有比Sobel更好用的Scharr算子,大家可以了解下:
sobel算子的API:sobel_image = cv2.Sobel(src, ddepth, dx, dy, ksize)
src:这是输入图像,通常应该是一个灰度图像(单通道图像),因为 Sobel 算子是基于像素亮度梯度计算的。在彩色图像的情况下,通常需要先将其转换为灰度图像。
ddepth:这个参数代表输出图像的深度,即输出图像的数据类型。在 OpenCV 中,-1 表示输出图像的深度与输入图像相同。
dx,dy:当组合为dx=1,dy=0时求x方向的一阶导数,在这里,设置为1意味着我们想要计算图像在水平方向(x轴)的梯度。当组合为 dx=0,dy=1时求y方向的一阶导数(如果同时为1,通常得不到想要的结果,想两个方向都处理的比较好 学习使用后面的算子)
ksize:Sobel算子的大小,可选择3、5、7,默认为3。
Laplacian算子
Laplacian算子就是与sobel算子不一样的层面,一维的二阶差分公式
。
而对于二维函数f(x,y),两个方向的二阶差分分别是:
合在一起就是:
提取前面提到的系数就能得到二维的Laplacion滤波核:
这就是Laplacian算子的图像卷积模板,有些资料中在此基础上考虑斜对角情况,将卷积核拓展为:
Laplacion的API:
cv2.Laplacian(src, ddepth)
src:这是输入图像
ddepth:这个参数代表输出图像的深度,即输出图像的数据类型。在 OpenCV 中,-1 表示输出图像的深度与输入图像相同。
这些算子的工作原理可以将核简单理解为 “滑动窗口”:用一个 3x3 的矩阵在图像上逐像素滑动,将窗口内的像素与算子矩阵的数值相乘后求和,结果就是该像素的梯度大小(横向或纵向)。例如,Sobel 算子的横向矩阵会突出水平方向的灰度变化(即垂直边缘),纵向矩阵则突出垂直方向的灰度变化(即水平边缘)。
二、边缘检测:从梯度到清晰边界
边缘是图像中灰度值剧烈变化的区域(比如物体与背景的交界处),而梯度的大小直接反映了这种变化的 “剧烈程度”—— 梯度越大,越可能是边缘。因此,边缘检测的核心逻辑就是:通过梯度处理找到梯度值超过阈值的像素,将其标记为边缘。但实际操作中,边缘检测远比 “找大梯度” 复杂,因为噪声会干扰梯度计算(噪声的灰度突变会被误判为边缘),且边缘往往是连续的线条,需要进一步优化。
1. 边缘检测的前提:降噪处理
梯度对噪声极其敏感,一个孤立的噪声点(比如椒盐噪声)会导致局部梯度骤增,被误判为边缘。因此,边缘检测的第一步通常是降噪预处理,最常用的方法是 “高斯模糊”:用高斯函数对图像进行平滑处理,削弱高频噪声(灰度突变),同时保留低频边缘信息(较大范围的灰度变化)。
2. 计算图像的梯度与方向
这里使用了sobel算子来计算图像的梯度值, 首先使用sobel算子计算中心像素点的两个方向上的梯度和
,然后就能够得到其具体的梯度值:
也可以使用G=|G_{x}+G_{y}|来代替。在OpenCV中,默认使用G=|G_{x}+G_{y}|来计算梯度值。
然后我们根据如下公式可以得到一个角度值:
这个角度值其实是当前边缘的梯度的方向。通过这个公式我们就可以计算出图片中所有的像素点的梯度值与梯度方向,然后根据梯度方向获取边缘的方向。
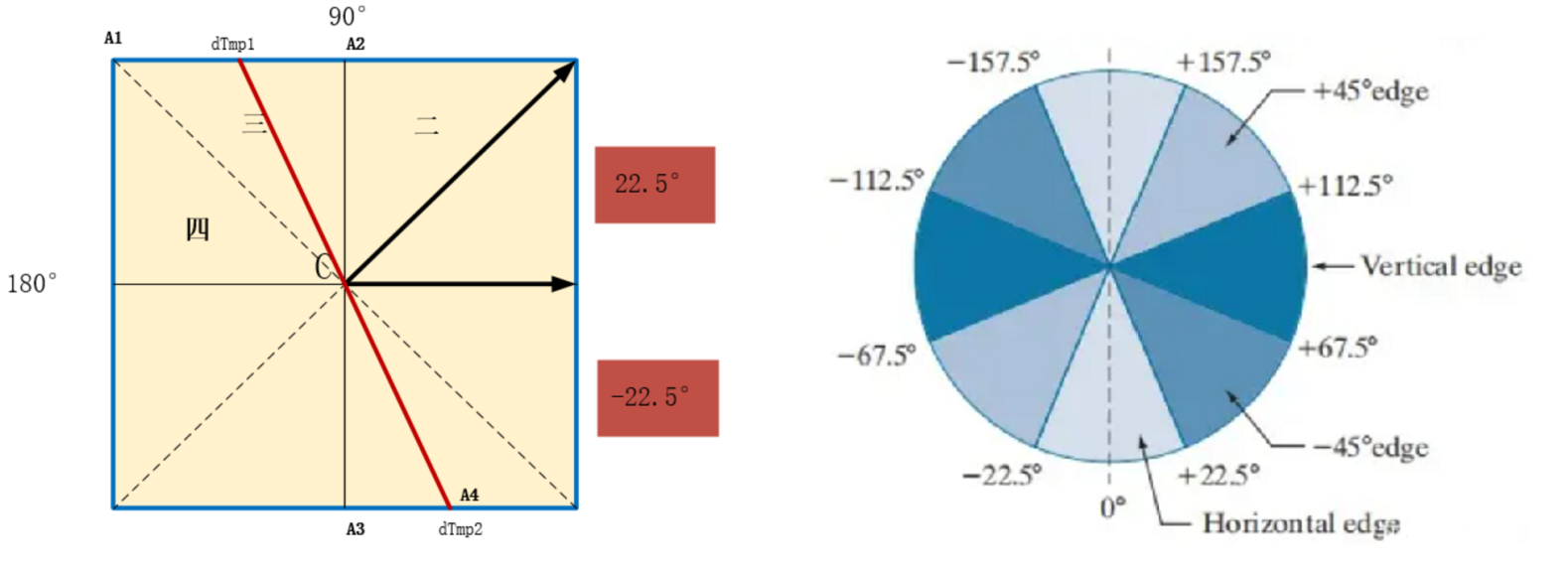
a). 并且如果梯度方向不是0°、45°、90°、135°这种特定角度,那么就要用到插值算法来计算当前像素点在其方向上进行插值的结果了,然后进行比较并判断是否保留该像素点。这里使用的是单线性插值,通过A1和A2两个像素点获得dTmp1与dTmp2处的插值,然后与中心点C进行比较(非极大值抑制)。如下左图
b). 得到的值之后,就可以对边缘方向进行分类,为了简化计算过程,OpenCV一般将其归为四个方向:水平方向、垂直方向、45°方向、135°方向。如右图,并且:
当值为-22.5°~22.5°,或-157.5°~157.5°,则认为边缘为水平边缘;
当法线方向为22.5°~67.5°,或-112.5°~-157.5°,则认为边缘为45°边缘;
当法线方向为67.5°~112.5°,或-67.5°~-112.5°,则认为边缘为垂直边缘;
当法线方向为112.5°~157.5°,或-22.5°~-67.5°,则认为边缘为135°边缘;
3.非极大值抑制
得到每个边缘的方向之后,其实把它们连起来边缘检测就算完了,但是为什么还有这一步与下一步呢?是因为经过第二步得到的边缘不经过处理是没办法使用的,因为高斯滤波的原因,边缘会变得模糊,导致经过第二步后得到的边缘像素点非常多,因此我们需要对其进行一些过滤操作,而非极大值抑制就是一个很好的方法,它会对得到的边缘像素进行一个排除,使边缘尽可能细一点。
在该步骤中,我们需要检查每个像素点的梯度方向上的相邻像素,并保留梯度值最大的像素,将其他像素抑制为零。假设当前像素点为(x,y),其梯度方向是0°,梯度值为G(x,y),那么我们就需要比较G(x,y)与两个相邻像素的梯度值:G(x-1,y)和G(x+1,y)。如果G(x,y)是三个值里面最大的,就保留该像素值,否则将其抑制为零。
4.双阈值筛选
经过非极大值抑制之后,我们还需要设置阈值来进行筛选,当阈值设的太低,就会出现假边缘,而阈值设的太高,一些较弱的边缘就会被丢掉,因此使用了双阈值来进行筛选,推荐高低阈值的比例为2:1到3:1之间,其原理如下图所示:
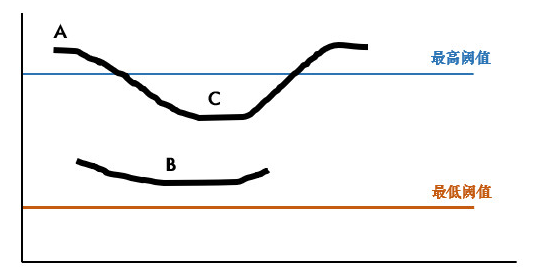
当某一像素位置的幅值超过最高阈值时,该像素必是边缘像素;当幅值低于最低像素时,该像素必不是边缘像素;幅值处于最高像素与最低像素之间时,如果它能连接到一个高于阈值的边缘时,则被认为是边缘像素,否则就不会被认为是边缘。也就是说,上图中的A和C是边缘,B不是边缘。因为C虽然不超过最高阈值,但其与A相连,所以C就是边缘。
注:双阈值筛选所设置的阈值不是像素值,而是梯度值的阈值
5.API的使用
edges = cv2.Canny(image, threshold1, threshold2),即使读到的是彩色图也可以进行处理。
-
image:输入的灰度/二值化图像数据。 -
threshold1:低阈值,用于决定可能的边缘点。 -
threshold2:高阈值,用于决定强边缘点。
三、理论到实践:梯度与边缘检测的应用
图像梯度处理和边缘检测是许多高级图像处理任务的基石,其应用遍布各行各业:
- 目标识别与追踪:在自动驾驶中,通过检测道路边缘、车辆轮廓的边缘,帮助车辆判断行驶边界和障碍物位置;
- 医学影像分析:在 CT 或 MRI 图像中,边缘检测可定位肿瘤、血管的边界,辅助医生诊断;
- 图像分割:将图像按边缘划分为不同区域(如前景与背景),为后续处理提供基础;
- 工业检测:通过检测产品表面的边缘缺陷(如裂缝、划痕),实现自动化质量控制。
总结
图像梯度是描述像素灰度变化的 “数学工具”,而边缘检测则是基于梯度寻找图像中 “有意义边界” 的技术。从简单的 Sobel 算子到复杂的 Canny 算法,每一种方法都在平衡精度、效率与抗噪声能力。理解梯度与边缘检测的原理,主要在于理解为什么梯度处理使用数学中的一阶方差和二阶方差且卷积核如何发挥作用,边缘检测主要在于边缘方向不一定会是常见的45,90等,如何确认图像的梯度和方向就是需要重点理解的。
