卷积神经网络：模型评估标准

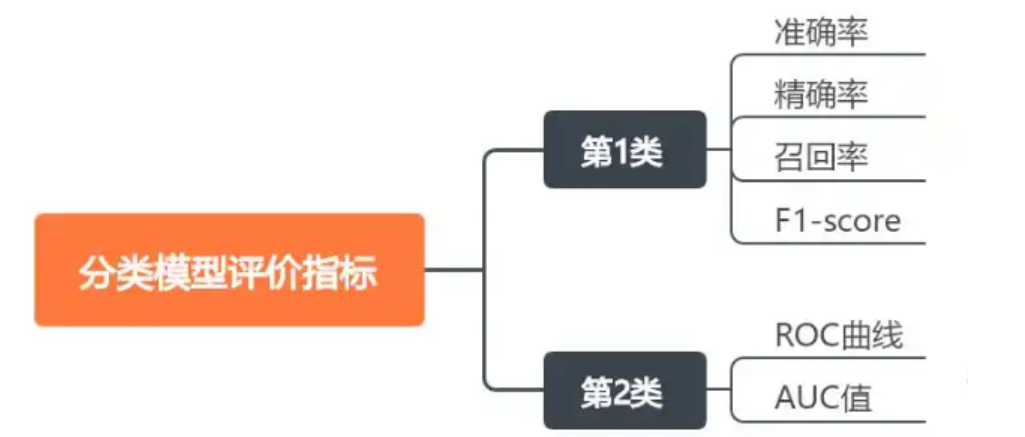
一、分类模型评价指标

在模型评估中，有多个标准用于衡量模型的性能，这些标准包括准确率（Accuracy）、精确率（Precision）、召回率（Recall）、F1 分数（F1-Score）等。

真正例（True Positive, TP）

定义 ：模型正确地预测为正类的样本数量。 通俗解释 ：假设你有一个垃圾邮件分类器，它会把邮件标记为垃圾邮件或非垃圾邮件。真正例就是那些被正确标记为垃圾邮件的邮件数量。

例子 ： 你有 100 封邮件。 其中 30 封是垃圾邮件。 模型正确地将 25 封垃圾邮件标记为垃圾邮件。 那么 TP = 25。

真负例（True Negative, TN）

定义 ：模型正确地预测为负类的样本数量。 通俗解释 ：假设你有一个垃圾邮件分类器，它会把邮件标记为垃圾邮件或非垃圾邮件。真负例就是那些被正确标记为非垃圾邮件的邮件数量。

例子 ： 你有 100 封邮件。 其中 70 封是非垃圾邮件。 模型正确地将 60 封非垃圾邮件标记为非垃圾邮件。 那么 TN = 60。

假正例（False Positive, FP）

定义 ：模型错误地预测为正类的样本数量。 通俗解释 ：假设你有一个垃圾邮件分类器，它会把邮件标记为垃圾邮件或非垃圾邮件。假正例就是那些被错误地标记为垃圾邮件的非垃圾邮件数量。

例子 ： 你有 100 封邮件。 其中 70 封是非垃圾邮件。 模型错误地将 10 封非垃圾邮件标记为垃圾邮件。 那么 FP = 10。

假负例（False Negative, FN）

定义 ：模型错误地预测为负类的样本数量。 通俗解释 ：假设你有一个垃圾邮件分类器，它会把邮件标记为垃圾邮件或非垃圾邮件。假负例就是那些被错误地标记为非垃圾邮件的垃圾邮件数量。

例子 ： 你有 100 封邮件。 其中 30 封是垃圾邮件。 模型错误地将 5 封垃圾邮件标记为非垃圾邮件。 那么 FN = 5。

• 真正例（TP） ：模型正确预测为正类的样本数量。

• 真负例（TN） ：模型正确预测为负类的样本数量。

• 假正例（FP） ：模型错误预测为正类的样本数量。

• 假负例（FN） ：模型错误预测为负类的样本数量。

二、准确率（Accuracy）

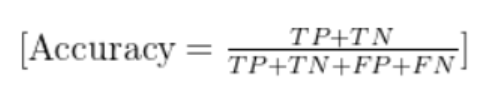
首先，我们需要明确数据的分类情况。这里有 3 个类别（0、1、2），先统计每个类别的预测正确与错误情况：

• 真实标签 y_true = [2, 0, 2, 2, 0, 1]
• 预测结果 y_pred = [0, 0, 2, 2, 0, 2]

逐样本对比：

样本索引	真实标签 (y_true)	预测标签 (y_pred)	结果
0	2	0	错误（2→0）
1	0	0	正确（0→0）
2	2	2	正确（2→2）
3	2	2	正确（2→2）
4	0	0	正确（0→0）
5	1	2	错误（1→2）

定义：所有预测正确的样本数占总样本数的比例。
公式：
Accuracy=总样本数预测正确的样本数​

计算：

• 预测正确的样本数：样本 1、2、3、4 → 共 4 个
• 总样本数：6 个
• 准确率 = 4/6 ≈ 0.6667（66.67%）

三、精确率（Precision）

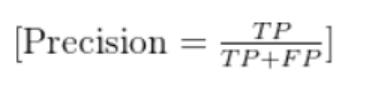
定义：针对某一类别，预测为该类别的样本中，实际确实是该类别的比例（“预测对的” 占 “预测为该类” 的比例）。
公式（以类别c为例）：
Precision(c)=所有预测为c的样本数预测为c且真实为c的样本数​

计算（分类别）：

• 类别 0：
  预测为 0 的样本：样本 0、1、4 → 共 3 个
  其中真实为 0 的样本：样本 1、4 → 共 2 个
  精确率 = 2/3 ≈ 0.6667（66.67%）

• 类别 1：
  预测为 1 的样本：0 个（所有预测中没有 1）
  精确率 = 0（或无定义，因分母为 0）

• 类别 2：
  预测为 2 的样本：样本 2、3、5 → 共 3 个
  其中真实为 2 的样本：样本 2、3 → 共 2 个
  精确率 = 2/3 ≈ 0.6667（66.67%）

注：多分类问题中，通常会计算 “宏平均精确率”（各类别精确率的平均值）或 “微平均精确率”（全局统计的精确率）。这里宏平均精确率 = (0.6667 + 0 + 0.6667)/3 ≈ 0.4444（44.44%）。

四、召回率（Recall）

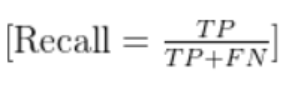
定义：针对某一类别，真实为该类别的样本中，被成功预测为该类别的比例（“预测对的” 占 “真实为该类” 的比例）。
公式（以类别c为例）：
Recall(c)=所有真实为c的样本数预测为c且真实为c的样本数​

计算（分类别）：

• 类别 0：
  真实为 0 的样本：样本 1、4 → 共 2 个
  其中预测为 0 的样本：样本 1、4 → 共 2 个
  召回率 = 2/2 = 1（100%）

• 类别 1：
  真实为 1 的样本：样本 5 → 共 1 个
  其中预测为 1 的样本：0 个
  召回率 = 0/1 = 0（0%）

• 类别 2：
  真实为 2 的样本：样本 0、2、3 → 共 3 个
  其中预测为 2 的样本：样本 2、3 → 共 2 个
  召回率 = 2/3 ≈ 0.6667（66.67%）

注：多分类问题中，宏平均召回率 = (1 + 0 + 0.6667)/3 ≈ 0.5556（55.56%）。

五、F1 分数（F1-Score）

定义：精确率和召回率的调和平均数，综合反映模型的稳健性（避免精确率高但召回率低，或反之）。
公式（以类别c为例）：
F1(c)=2×Precision(c)+Recall(c)Precision(c)×Recall(c)​

计算（分类别）：

• 类别 0：
  F1 = 2 × (0.6667 × 1) / (0.6667 + 1) = 2 × 0.6667 / 1.6667 ≈ 0.8（80%）

• 类别 1：
  F1 = 2 × (0 × 0) / (0 + 0) → 0（因精确率和召回率均为 0）

• 类别 2：
  F1 = 2 × (0.6667 × 0.6667) / (0.6667 + 0.6667) = 2 × 0.4444 / 1.3334 ≈ 0.6667（66.67%）

注：多分类问题中，宏平均 F1 = (0.8 + 0 + 0.6667)/3 ≈ 0.4889（48.89%）。

总结

指标	整体 / 宏平均结果
准确率（Accuracy）	66.67%
精确率（Precision）	44.44%
召回率（Recall）	55.56%
F1 分数（F1-Score）	48.89%

六、混淆矩阵

混淆矩阵是评估分类问题的基础工具，它是一个表格，显示了分类算法的预测结果与真实标签之间的关系。对于二分类问题，混淆矩阵包含真正例（TP）、真负例（TN）、假正例（FP）和假负例（FN）。这些值是计算其他评估指标的基础。混淆矩阵不仅提供了一个直观的视觉表示，还允许我们深入了解模型在各个类别上的表现，特别是当处理不平衡数据集时，混淆矩阵可以揭示模型是否倾向于错误地将一个类别分类为另一个类别。

混淆矩阵（Confusion Matrix）是机器学习和统计学中评估分类模型性能的重要工具，它以矩阵形式直观展示模型对各类别的预测结果与真实标签的匹配情况，能帮助我们深入理解模型的错误类型（如将 A 类误判为 B 类的频率）。

6.1混淆矩阵的基本结构

混淆矩阵是一个 n×n 的方阵（n 为类别数量），行代表 真实标签，列代表 预测标签。每个单元格 (i,j) 表示 “真实标签为 i 且被预测为 j” 的样本数量。

以 二分类问题（最常见场景）为例，混淆矩阵为 2×2 结构，核心概念如下：

真实标签 \ 预测标签	预测为正例（Positive）	预测为负例（Negative）
正例（Positive）	TP（True Positive）	FN（False Negative）
负例（Negative）	FP（False Positive）	TN（True Negative）

• TP：真实为正例，预测也为正例（正确预测）。
• FN：真实为正例，却预测为负例（漏检，“假阴性”）。
• FP：真实为负例，却预测为正例（误检，“假阳性”）。
• TN：真实为负例，预测也为负例（正确预测）。

6.2多分类问题的混淆矩阵

对于 n 个类别的分类任务（如识别手写数字 0-9），混淆矩阵为 n×n 结构，每个单元格 (i,j) 表示 “真实类别为 i 且被预测为 j” 的样本数。

例如，用本文开头的三分类数据（类别 0、1、2）：

• ytrue​=[2,0,2,2,0,1]
• ypred​=[0,0,2,2,0,2]

其混淆矩阵为 3×3：

真实标签 \ 预测标签	预测 0	预测 1	预测 2
真实 0	2	0	0
真实 1	0	0	1
真实 2	1	0	2

• 对角线（如真实 0→预测 0、真实 2→预测 2）表示预测正确的样本数，总和为模型正确预测的总样本数。
• 非对角线（如真实 2→预测 0、真实 1→预测 2）表示预测错误的样本数，可直观看到模型容易将哪些类别混淆。

6.3混淆矩阵的核心作用

1. 计算评估指标
   几乎所有分类指标（准确率、精确率、召回率、F1 分数等）都可通过混淆矩阵推导：

   • 准确率（Accuracy）：TP+TN+FP+FNTP+TN​（整体正确率）
   • 精确率（Precision）：TP+FPTP​（预测为正例中真正为正例的比例）
   • 召回率（Recall）：TP+FNTP​（真实正例中被正确预测的比例）
   • F1 分数：2×Precision+RecallPrecision×Recall​（精确率和召回率的调和平均）

2. 分析错误模式
   混淆矩阵能揭示模型的 “薄弱环节”，例如：

   • 在图像分类中，模型是否经常将 “猫” 误判为 “狗”？
   • 在疾病诊断中，是否有大量 “真阳性” 被漏检（FN 过高）？

3. 指导模型优化
   根据错误模式调整模型：若某类别的 FN 过高（召回率低），可增加该类样本的训练数据；若某类别的 FP 过高（精确率低），可优化特征以减少误判。

6.4如何绘制混淆矩阵？

在 Python 中，可使用 scikit-learn 生成混淆矩阵，再用 matplotlib 或 seaborn 可视化：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import confusion_matrixplt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号# 示例数据
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])
classes = [0, 1, 2]  # 类别标签# 计算混淆矩阵
cm = confusion_matrix(y_true, y_pred)# 可视化
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=classes, yticklabels=classes)
plt.xlabel('预测标签')
plt.ylabel('真实标签')
plt.title('混淆矩阵')
plt.show()

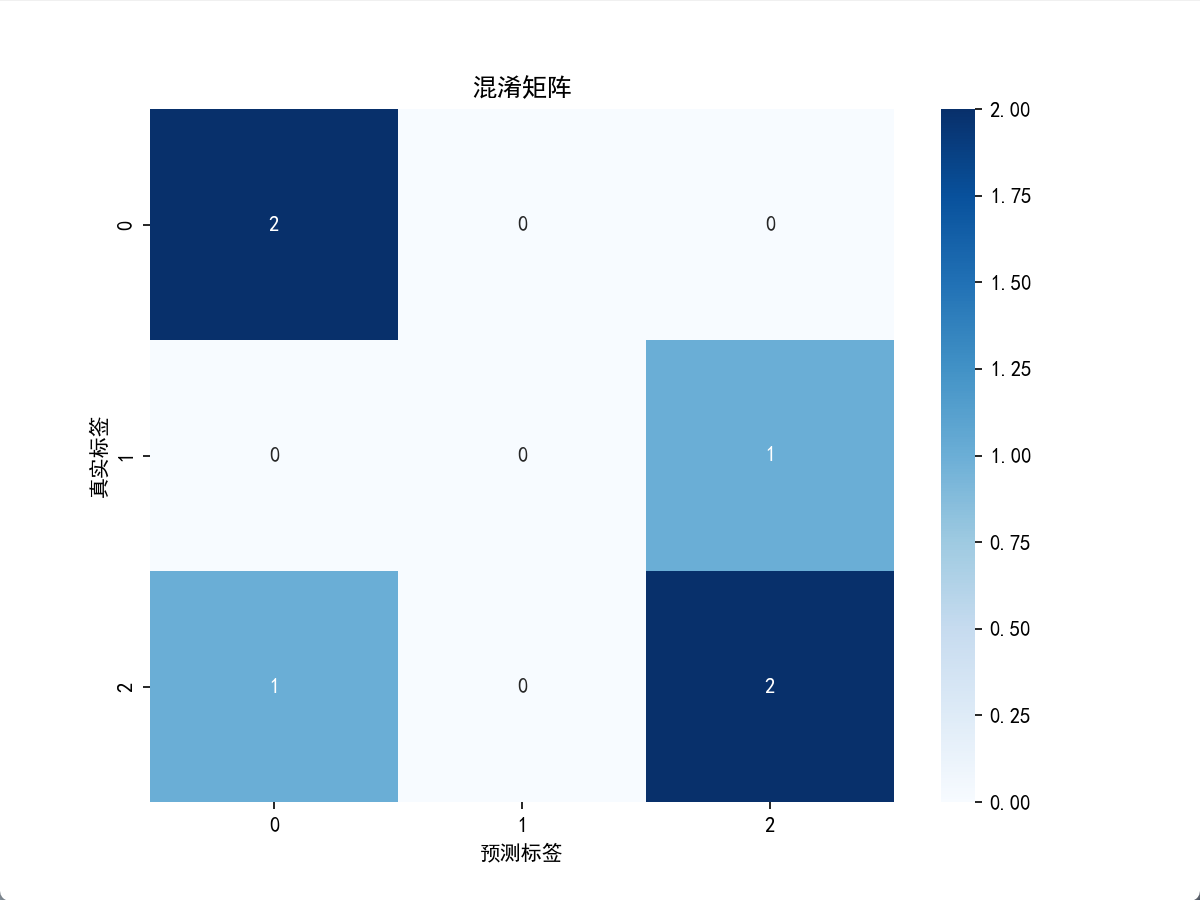
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score,f1_score
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns# 假设我们有以下真实标签和预测结果
y_true = np.array([2, 0, 2, 2, 0, 1])
y_pred = np.array([0, 0, 2, 2, 0, 2])# 计算准确率
accuracy = accuracy_score(y_true, y_pred)
print("准确率：", accuracy)# 计算精确率
precision = precision_score(y_true, y_pred, average='macro')
print("精确率：", precision)# 计算召回率
recall = recall_score(y_true, y_pred, average='macro')
print("召回率：", recall)# 计算F1分数
f1 = f1_score(y_true, y_pred, average='macro')
print("F1分数：", f1)# 计算混淆矩阵
cm = confusion_matrix(y_true, y_pred)# 使用Seaborn的heatmap函数来可视化混淆矩阵
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.title('Confusion Matrix')
plt.show()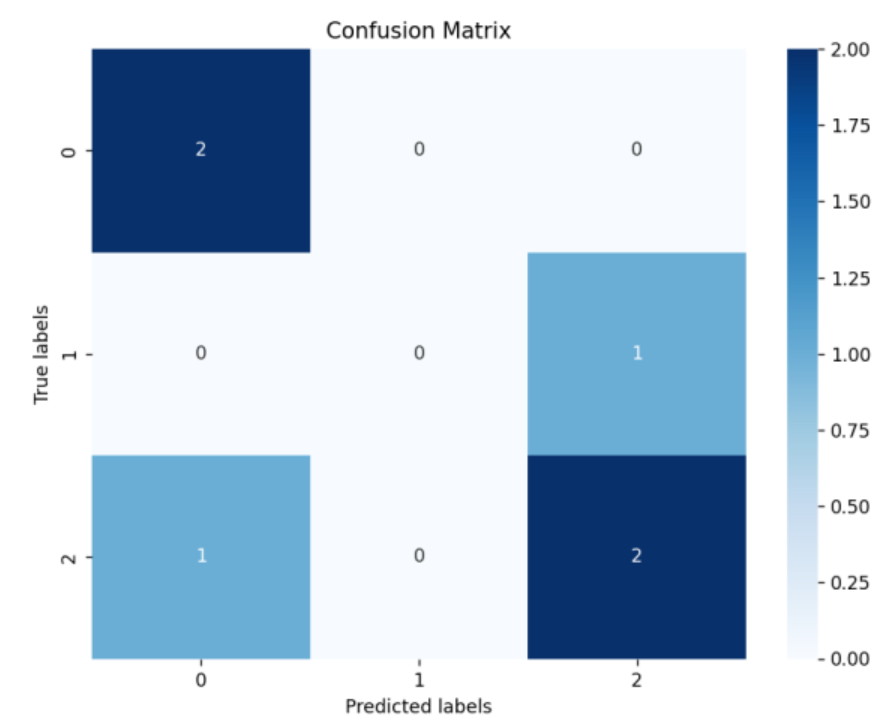

运行后会生成带数值标注的热力图，颜色越深表示该单元格的样本数越多，直观展示分类结果。

6.5总结

混淆矩阵是分类模型评估的 “基石”，它不仅能帮助计算各类量化指标，更能通过可视化直观呈现模型的错误分布，为模型优化提供具体方向。无论是二分类还是多分类问题，理解混淆矩阵都是数据分析和机器学习中的必备技能。

七、ROC曲线和AUC值（不怎么用）

ROC曲线是一个性能度量，显示了在不同阈值设置下模型的真正例率（召回率）和假正例率的关系。AUC值表示ROC曲线下的面积，用于衡量模型的整体性能，AUC值越高，模型性能越好。ROC曲线和AUC值是评估模型区分不同类别能力的重要工具，尤其在二分类问题中非常实用。

7.1ROC 曲线的基本概念

ROC 曲线以假正例率（False Positive Rate, FPR） 为横轴，以真正例率（True Positive Rate, TPR） 为纵轴，描述了模型在不同阈值下的分类性能。

1. 核心指标定义

• 真正例率（TPR，又称灵敏度、召回率）：
  真实正例中被正确预测为正例的比例，反映模型对正例的识别能力。
  TPR=TP+FNTP​

• 假正例率（FPR，又称 1 - 特异度）：
  真实负例中被错误预测为正例的比例，反映模型的误判率。
  FPR=FP+TNFP​

  （注：TP、TN、FP、FN 的定义见混淆矩阵相关内容）

2. ROC 曲线的绘制逻辑

分类模型（如逻辑回归、SVM 等）通常会输出样本属于正例的概率分数（而非直接输出类别）。通过调整分类阈值（如将概率≥0.5 的样本判为正例），可得到不同的 TPR 和 FPR：

• 阈值越低：更多样本被预测为正例，TPR 升高（识别更多正例），但 FPR 也升高（误判更多负例）。
• 阈值越高： fewer 样本被预测为正例，FPR 降低（误判减少），但 TPR 也降低（可能漏检正例）。

ROC 曲线通过遍历所有可能的阈值，计算对应的 (TPR, FPR) 点并连接而成，完整反映模型在 “灵敏度 - 特异度” 权衡下的整体表现。

7.2ROC 曲线的解读

1. 理想模型：
   当阈值调整时，能 100% 识别正例（TPR=1）且 0 误判负例（FPR=0），ROC 曲线会直接从 (0,0) 垂直上升到 (0,1)，再水平向右到 (1,1)，形成一个直角。

2. 随机猜测模型：
   若模型无预测能力（如随机猜测），TPR 与 FPR 相等，ROC 曲线为一条从 (0,0) 到 (1,1) 的对角线（斜率 = 1）。

3. 实际模型：
   好的模型 ROC 曲线应尽可能靠近左上角（高 TPR、低 FPR），且整体在随机猜测的对角线上方。两条 ROC 曲线比较时，上方的曲线对应性能更优的模型。

7.3AUC 值（曲线下面积）

AUC 是 ROC 曲线与横轴之间的面积，取值范围为 [0, 1]，用于量化评估模型的整体性能。

1. AUC 的物理意义

• AUC=1：完美模型，能完全区分正负例（TPR=1 且 FPR=0）。
• AUC=0.5：模型性能与随机猜测相同（如抛硬币）。
• AUC<0.5：模型性能差于随机猜测（实际应用中可反向预测改善）。
• AUC 越接近 1：模型区分正负例的能力越强。

更直观地说，AUC 表示 “随机抽取一个正例和一个负例，模型将正例预测为正例的概率高于负例的概率” 的可能性。例如，AUC=0.8 意味着有 80% 的概率，模型能正确区分随机选取的正负例。

2. AUC 的优势

• 对阈值不敏感：ROC 曲线和 AUC 综合了所有阈值下的表现，避免了单一阈值的局限性。
• 适用于不平衡数据：在正负样本比例悬殊时（如疾病数据中患者仅占 1%），AUC 比准确率（Accuracy）更能反映模型真实性能（准确率可能因多数类占优而虚高）。

7.4如何计算和绘制 ROC 曲线与 AUC？

在 Python 中，可使用scikit-learn快速实现：

from sklearn.metrics import roc_curve, roc_auc_score
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import matplotlib.pyplot as plt
import numpy as npplt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号# 假设我们有一个数据集
X = np.array([[0, 0], [1, 1], [2, 0], [2, 2], [0, 1]])
y = np.array([1, 1, 0, 1, 0])plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red', label='Class 0')
plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue', label='Class 1')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.title('Data Points by Class')
plt.grid(True)
plt.show()# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42)print("--------训练样本-----------")
print(X_train,y_train)
print("--------测试样本-----------")
print(X_test,y_test)# 训练一个随机森林分类器
clf = RandomForestClassifier(n_estimators=100, random_state=42)
clf.fit(X_train, y_train)# 预测概率
y_scores = clf.predict_proba(X_test)[:, 1]# 计算ROC曲线和AUC值
fpr, tpr, thresholds = roc_curve(y_test, y_scores)
auc = roc_auc_score(y_test, y_scores)# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正例率')
plt.ylabel('真正例率')
plt.title('ROC曲线')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()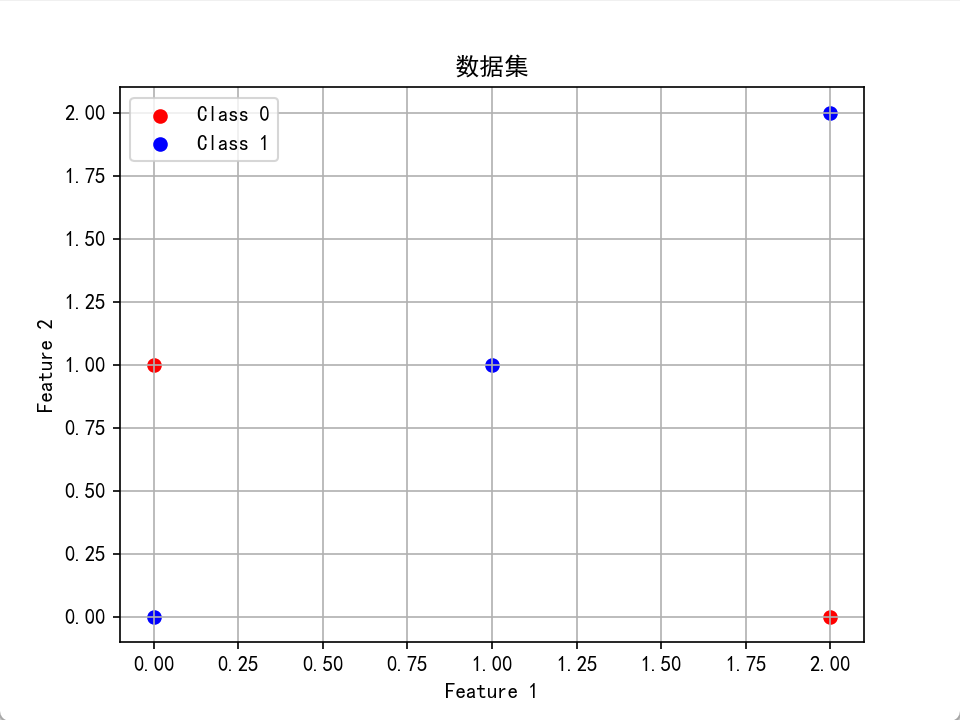

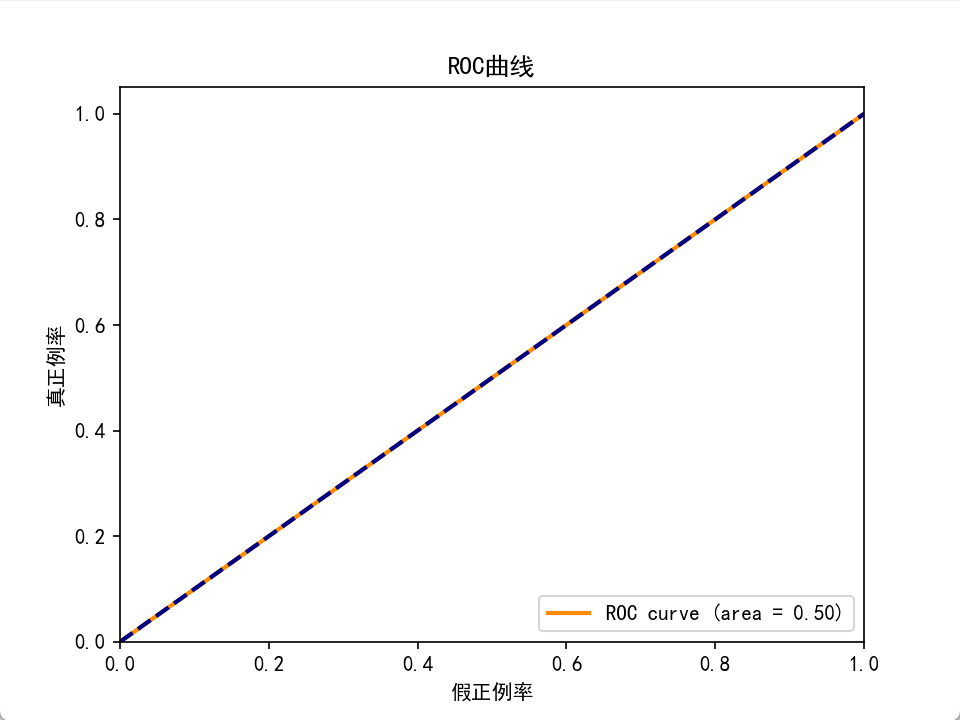
运行结果会显示一条 ROC 曲线和对应的 AUC 值，直观反映模型性能。

7.5注意事项

1. 多分类问题：ROC 曲线本质是二分类工具，多分类场景需通过 “一对多”（One-vs-Rest）或 “一对一”（One-vs-One）策略转化为多个二分类问题，再计算平均 AUC。
2. 数据不平衡的局限性：虽然 AUC 对不平衡数据的鲁棒性优于准确率，但当负例数量极多时，FPR 的微小变化可能被放大，需结合精确率 - 召回率曲线（PR 曲线）综合评估。
3. 阈值选择：AUC 反映整体性能，但实际应用中需根据业务需求选择阈值（如疾病诊断更关注高召回率以减少漏诊，垃圾邮件过滤更关注高精确率以减少误判）。

总结

ROC 曲线和 AUC 值是评估二分类模型的黄金标准：ROC 曲线通过可视化展示模型在不同阈值下的灵敏度与特异度权衡，AUC 则通过数值量化模型的整体区分能力。二者结合能全面反映模型性能，尤其适合不平衡数据或需要权衡错误类型的场景。