11-1 浅层神经网络及计算前向传播

浅层神经网络

之前看了单神经元神经网络，就是这个

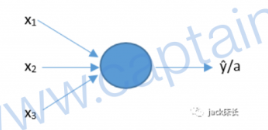
因为神经网络太简单，所以识别率不高。

这个唯一神经元，负责执行了如下运算

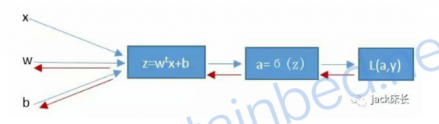
通过x，w，b计算得到z，然后由z得到a，a即预测结果，通过a和真是标签y构建损失函数L计算损失。同时反向传播，计算w和b关于损失函数的偏导数，梯度下降，然后前向、反向……不停优化。

这里看下稍复杂一点的神经网络----浅层神经网络。

对于多神经元神经网络，流程一样，即重复单神经元的流程。这里是一个多神经元神经网络

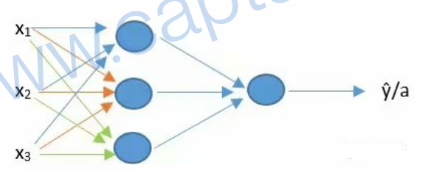
拆分下即：（三个加在一起了）

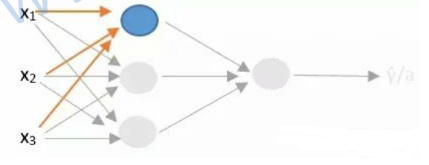
最前面负责输入特征的层叫做输入层，但统计层数的时候不会把这一层计算在内，所以这是一个两层的神经网络（虽然看着是3层），最后一层叫做输出层；中间的所有层统称为隐藏层。

计算浅层神经网络的前向传播

这个两层神经网络如何运算呢？

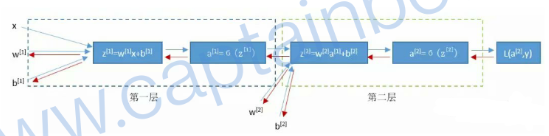
第一步：计算第一层3个神经元的a

第二步：3个a当做x输入第二层的神经元中进行计算

上面的w[1]表示的是第一层的神经元关于输入层x的权重，所以w[1]是一个3*3的矩阵，因为第一层有3个神经元，每一个神经元都有3个特征输入。

即这样：上角标表示第几层，下角标表示该层第几个神经元。（前边是第一层三个神经元，按前边的走，这里多的一个码掉了）

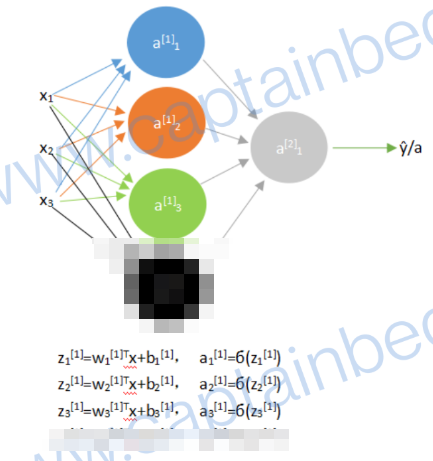
现在第一层只有三个神经元，算三次，还能接受。

但如果成百上千呢？回忆下之前的内容，向量化！

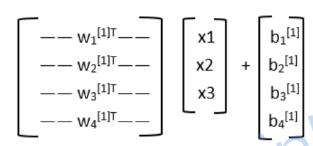
要进行向量化，关键点是将第一层的3个权重组合成一个矩阵。

如下图所示，w1[1]T是一个行向量，表示第一层第一个神经元关于3个输入特征的3个权重列向量转置

w2[1]T是一个行向量，表示第一层第二个神经元关于3个输入特征的3个权重列向量转置

三个这样的行向量组成了一个3*3的矩阵（图上是4个但是按咱们之前的3个例子来哈，图没码忽略下）

（没看懂？没关系，结合10种的内容反复看看，盘一下）

这里说到wT是行向量，维度（1，特征个数个权重）

wT要和特征相乘，结合矩阵的乘法 = wT的第一行*所有特征 = 权重列向量转置*所有特征 = w1*x1 + w2*x2 + w3*x3 

这就好理解了，比如我们有一个样本即x

x样本的特征向量：

1 

2

3

假设第一个神经元的权重w还用之前的2 7 2 （列向量，因为要对应特征

第一个神经元的第一个样本的计算wT*x1=22

这里注意，不同神经元的w和b不同

所以上边的向量化意思就是每个神经元的w放一起，然后所有输入放一起，所有b放一起，批量计算z

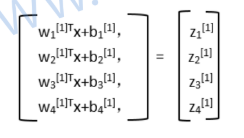
所以计算的三次就被向量化成这组式子（可以一次性计算第一层所有神经元的a，不管多少个）

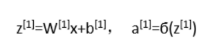
同理，第二层的a[2]用第一层的a[1]作为x输入，也这样

但是！！

到现在为止仅计算了单训练样本，然而训练神经网络需要非常多训练样本，所以，常规就是for一下。m表示训练样本的数量

之前学过了，这样效率很低，要把for也向量化，即把所有样本的特征列向量x组合成一个矩阵，酱紫

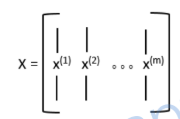
这样for就干掉了，变这样

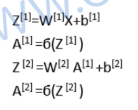
最终会得到Z和A两个矩阵

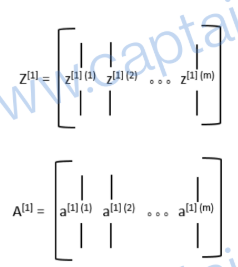
矩阵中的每一个列向量对应一个样本，如Z[1](1)是第一个样本第一层的z，a[1](2)是第二个样本第一层的a

最终计算损失